移动机器人预设性编队控制算法研究
李海婷,张鹏超,呙生富,刘亚恒,徐鹏飞
(1.陕西理工大学 电气工程学院,陕西汉中 723001;2.陕西理工大学 陕西省工业自动化重点实验室,陕西汉中 723001)
移动机器人的编队广泛应用于远地作业、协助军事运动、震后搜索与营救、自动化工厂、农业生产及防疫消杀场合中,是多智能体领域的重要研究方向之一[1-2]。常用的编队控制方法有跟随领航者法、人工势场法、基于行为法等[3]。近年来,随着智能控制技术的大力发展,遗传算法、粒子群优化算法[4]、模糊控制[5]、滑模控制[6-9]、神经网络控制[10]、预测控制[11]等被应用到多智能体编队中来,其中遗传算法、粒子群优化算法属于同一类型的路径搜索算法,会出现局部最优、死锁问题;神经网络存在“黑匣子”和学习速度慢问题;预测控制算法中存在大量参数,当有扰动时鲁棒性难以保证;而自适应模糊控制算法因其不依赖于被控对象的精确模型,与滑模控制相结合具有高鲁棒性和易于软件实现的特点被广泛应用。
传统的模糊滑模控制法已在多移动机器人编队控制中得到应用,虽可以满足控制系统对实时性、自适应调整的要求,但在编队过程中仍出现控制精度差、自适应能力有限、振荡等问题。为此,Chen等[12]提出一种自适应模糊滑膜控制器,提高了系统的自适应性,但响应时间明显增加。Djelal和Nair等[13-14]从动力学的角度,利用模糊逻辑系统补偿控制率中的不确定性,有效减小了系统抖振,但控制精度有待提高。在实际应用中,机器人在编队过程中控制精度低、通讯范围有限时机器人会掉队造成任务失败,预设性能约束是解决该问题的方法之一。在预设条件下,Bechlioulis和Dai等[15-16]设计了一种具有最小复杂度的鲁棒分布式控制律,但跟踪曲线抖动范围大,有较大的超调,Verginis等[17]研究了具有双积分动力学编队控制问题,但控制系统响应速度较低,在此基础上,Dai等[18]引入tan型李亚普诺夫函数,设计虚拟控制器完成了圆形编队,通过控制输入力矩使距离误差和角度误差控制在一定范围内,跟踪误差精确度较低,且跟踪曲线有微小的抖动。
本文通过综合考虑机器人自身安全距离、角度约束和外部环境未知扰动影响,提出一种新的预设性编队控制算法,通过设计预设性能函数来约束跟踪误差范围,设计滑膜控制率来逼近理想输入状态量,利用模糊逻辑消除系统抖振,并采用Lyapunov理论分析证明了该控制系统的稳定性,在仿真实验研究中,通过与文献[18]提出的tan型障碍李亚普诺夫算法跟踪误差和队形整体评价函数相比较,对该算法的准确性以及有效性进行分析。
1 移动机器人编队基本模型
1.1 移动机器人运动-动力学模型
针对非完整轮式移动机器人Kobuki建立模型,机器人底盘主要由两个后轮和一个前轮组成,后轮用来驱动,前轮用来平衡系统,见图1。
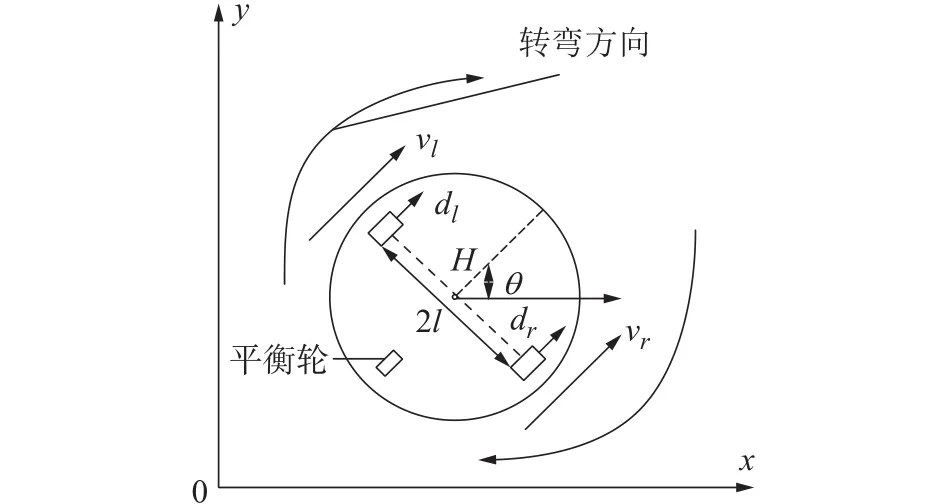
图1 移动机器人运动-动力学模型
由图1可得机器人的动力学方程[19]:
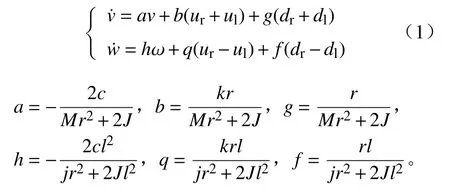
式中:j为机器人绕中心轴旋转的转动惯量;M为机器人的质量;J为轮子的转动惯量;c为粘性阻尼系数;k为放大系数;ul、ur为左右轮的输入力矩;r为车轮半径;dl、dr分别为机器人系统左右轮的扰动力矩;l为左右两轮中心线间距离的1/2;θ为机器人的航向角;ω为角速度;v为线速度。

由图1得机器人的运动学方程[20]为
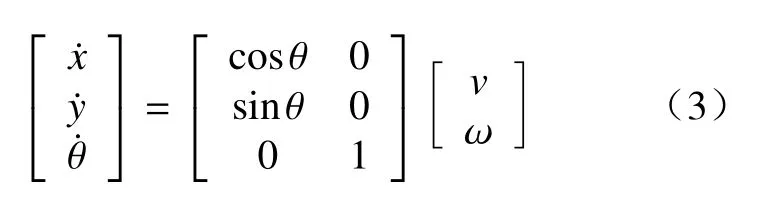
1.2 虚拟领航-跟随者相对运动模型
为减小跟随者对领航者的过度依赖,避免链式结构造成的跟踪误差累积问题,采用虚拟领航-跟随运动结构,参与编队的i(i= 1,2,3,···,n)个机器人为跟随者,以虚拟领航机器人为参考点,各机器人与虚拟领航者保持一定的距离和角度实现编队。虚拟领航者与跟随者相对运动模型如图2所示。
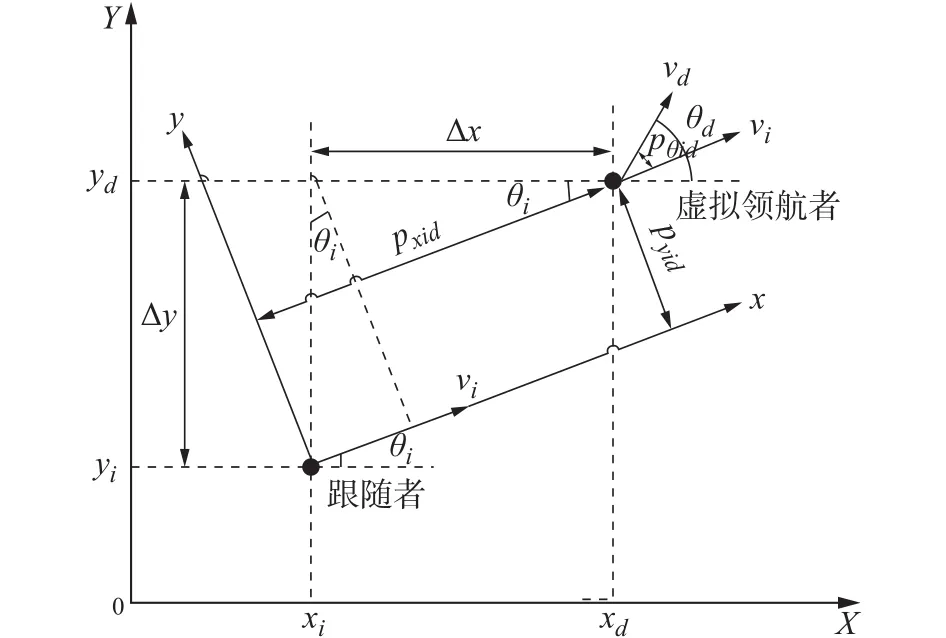
图2 跟随者与虚拟领航者相对运动位姿模型
设虚拟领航者的位姿qd=[xdydθd]T,ud=[vdwd]T, 跟 随 机 器 人 的 位 姿qi=[xiyiθi]T,ui=[viwi]T,二者之间的相对位姿p=[pxidpyidpβid]T,由图2可得跟随机器人i与虚拟领航者的相对位姿方程为
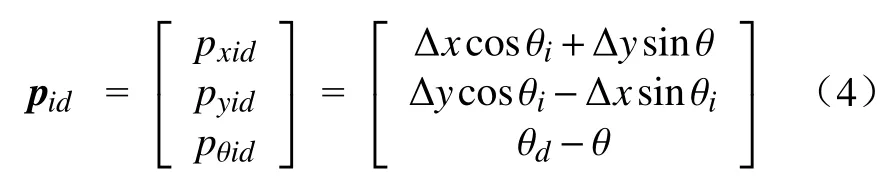
式中: Δx=xd−xi; Δy=yd−yi。
2 控制器的设计及稳定性分析
2.1 问题描述
为了直观的描述控制系统,确定输入输出量及控制目标,联立式(2)~ 式(4)得控制系统运动-动力学状态方程为
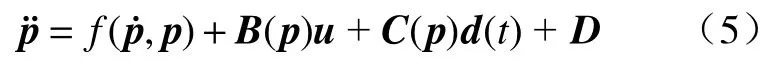
其中:
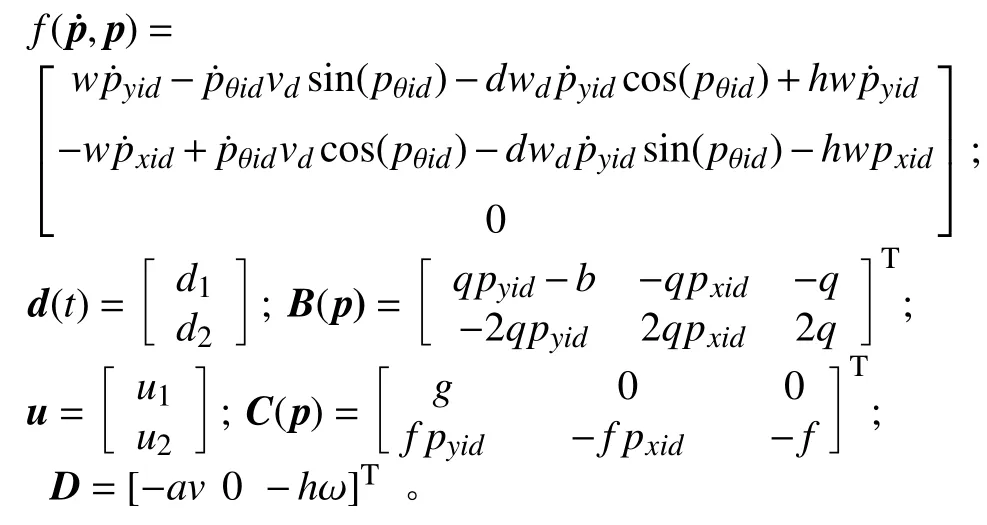
式中:p为 相对位置的输出;u为 控制输入;d(t)为未知扰动。定义 δr=[δxidδyidδθid]T为相对位姿的理想值,则跟踪误差e=pid−δid,对其求二阶导可得
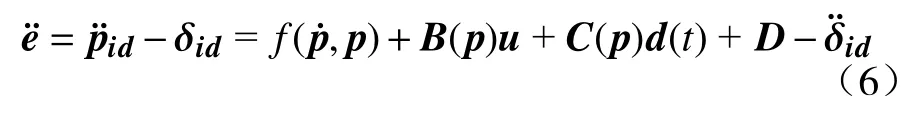
取预设性能指标函数为 λ (t),设计为λ(t)=(λ(0)−λ∞)e−βt+λ∞, 其 中 , β >0, 0 < |e(0)| < λ (0)则 λ (t)>0,按指数快速收敛到 λ∞的值。控制目标为通过设计控制率使跟随机器人与虚拟领航者保持一定的距离和角度,编队控制跟踪误差在运动过程中始终处于预设的范围内,从而保持控制系统的高精度跟踪和稳定性。
2.2 预设误差性能函数设计
为了保证跟踪误差快速收敛,并达到一定的收敛精度,现取单一变量跟踪误差进行分析,并设跟踪误差为[20]

其中S(ε)=e(t)/λ(t),且S(ε)需满足如下要求:
1)S(ε)为光滑连续的单调递增函数;
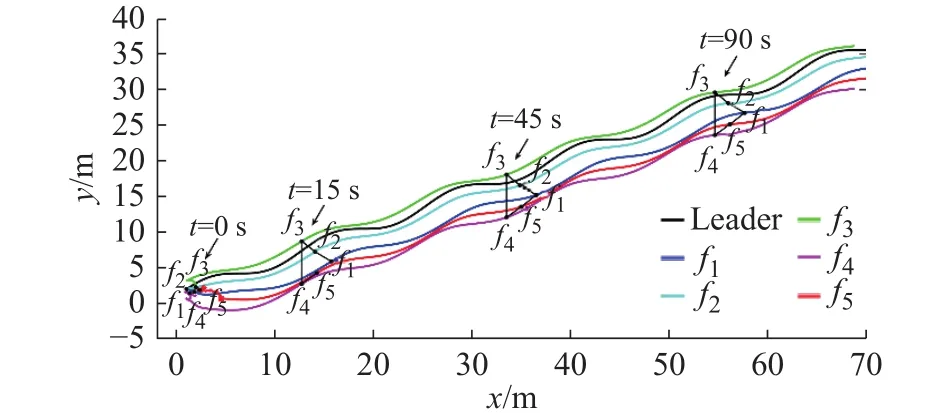
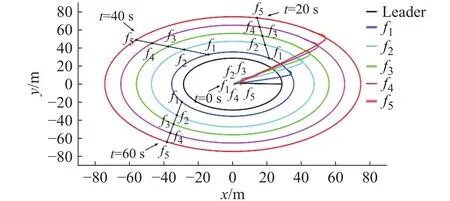
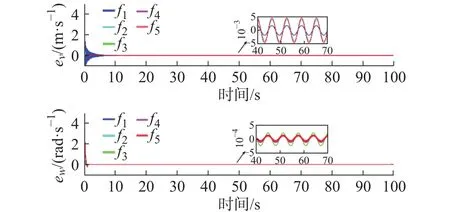
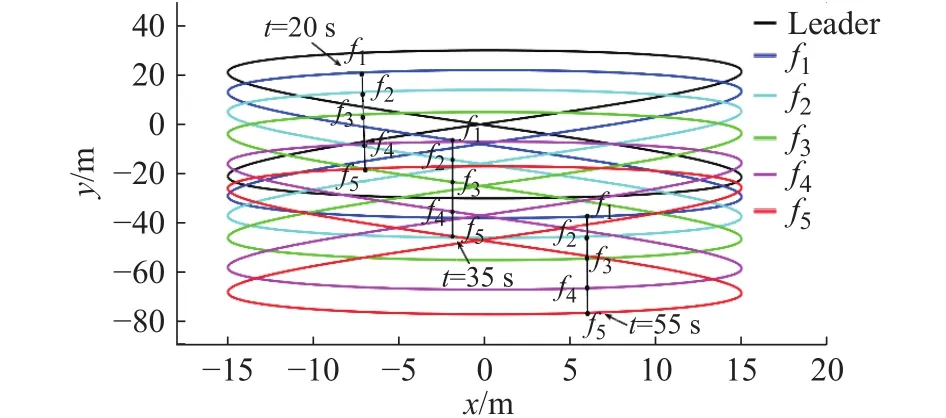
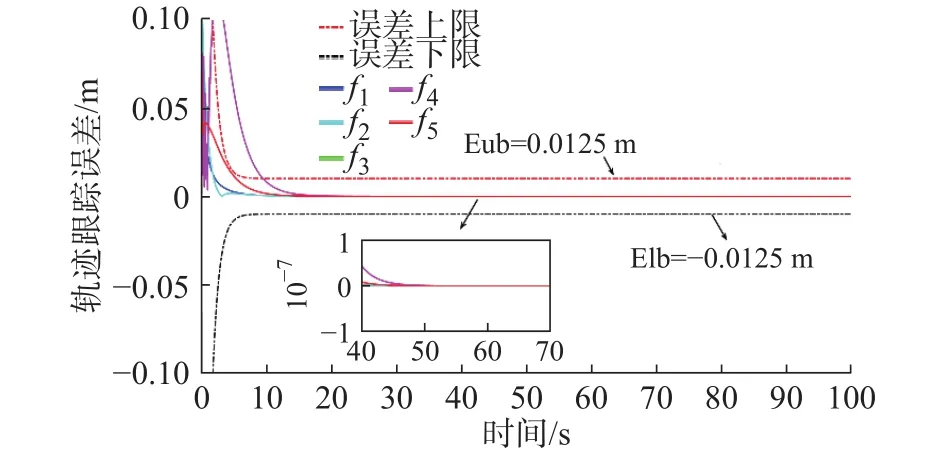
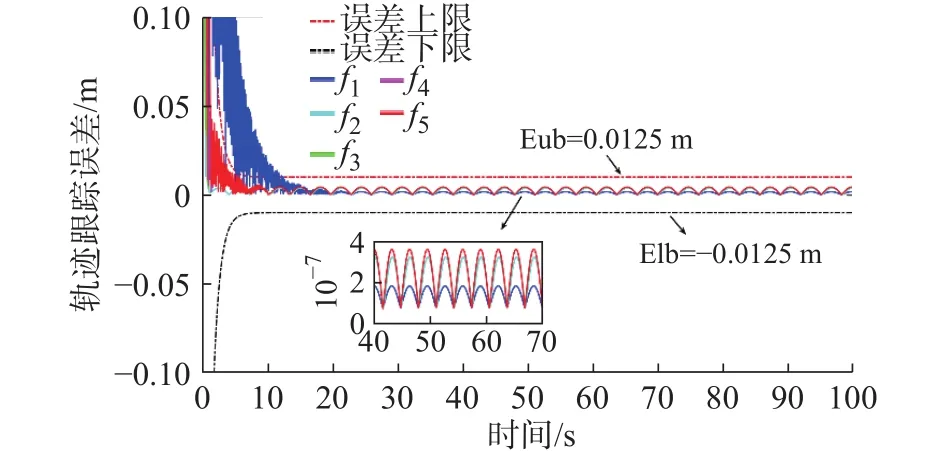
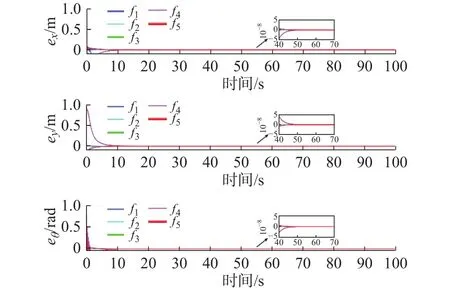
2)−1 3)S(ε)∞=1,S(ε)−∞= −1。 根据上述要求设计误差性能函数S(ε)为双曲正切函数,表示为 由于 − 1 从而e(t)的收敛集合 ℜ ={e∈R:|e(t)|≤ λ∞},通过对跟踪误差的限定,可实现理想输出和输出值范围的限定。 根据双曲正切函数的性质,函数S(ε)的反函数为ε=0.5[ln(λ+e)−ln(λ−e)],则: 由式(10)、式(11)可得 取滑模函数为 则有 其中u1=M3B(p)u。设控制量u1为 因滑模存在条件为 σ σ˙<0,K(t)是保证运动到达滑模面的增益,其值必须满足消除不确定项的影响的要求,所以设计模糊规则:ss˙>0和K(t)同增同减。由模糊规则可设计关于 σ σ˙和K(t)关系的模糊系统,在该系统中, σ σ˙为输入,K(t)为输出。输入输出隶属函数如图3和图4所示。 图3 输入变量隶属函数 图4 输出变量隶属函数 式中G为 比例系数,G>0。用代替式(15)中的K(t),则u1变为 则控制率为 定义lyapunov函数为 则有 为使V(t)指数收敛于零,则需 σ 收敛于零,由式(13)可得,ε˙和 ε指数收敛于零,收敛速度决定于控制率中的 η值。由于双曲正切函数为单调递增函数,函数S(ε)有界且单调收敛于零,且e(t)的收敛范围取决于式(9)。 根据双曲正切函数导数的性质可得,S˙(ε)=(1−S2(ε))ε˙,S˙ (ε)指数收敛于零,又由 λ指数收敛于λ∞,λ˙ 指数收敛于零, λ˙S和Sλ˙都不是单调的指数收敛,则e˙(t)=λ˙S+Sλ˙为单调收敛于零,即控制系统是渐近稳定的。 为验证所设计的预设性编队控制算法的准确性和有效性。假设参与编队的机器人个数为5,分别取系统控制参数M= 20 kg,j= 0.162 kg·m2,J= 0.1 kg·m2,l= 0.27 m,r= 0.1 m,k= 1,c= 0.01,取机器人的线速度 1 m/s,角速度为 0.6 rad/s,自身安全距离为 0.3 m,角度约束为 π /2,虚拟领航者与跟随者相对角度和距离由队形轨迹设定,且虚拟领航者轨迹已知并取λ(0)=0.51, λ∞=0.001,η=10, β =5,输入扰动分别为d1=sin(t)+cos(t) N/m,d2=sin(t)−cos(t) N/m,采用控制率式(18)。在相同初始条件下,本文所提控制算法表示为A算法,文献[18]所提tan型障碍李亚普诺夫算法为B算法,仿真试验结果如图5~图14所示。 图5 三角形-曲线轨迹编队 图6 直线形-异构圆形轨迹编队 图14 B 算法跟随者速度跟踪误差 图5~图8为A算法下不同队形的编队轨迹,可看出机器人在编队形成后一起运动的任意时刻,跟随机器人始终与虚拟领航者保持相同的距离和角度稳定运动,且无碰撞、掉队现象;图9和图10为跟随机器人在两种控制算法下与虚拟领航机器人相对位姿综合跟踪误差;图11和图12为两种控制算法下各跟随机器人在x轴方向、y轴方向及航向角位置跟踪误差;图13和图14为各跟随机器人的线速度与角速度跟踪误差。现对控制精度、控制系统响应速度、曲线的光滑程度即稳定性进行对比分析。 图8 8 字形编队轨迹 图9 A 算法跟随者轨迹跟踪误差 图10 B 算法跟随者轨迹跟踪误差 图11 A 算法跟随者位置跟踪误差 图12 B 算法跟随者位置跟踪误差 图13 A 算法速度跟踪误差 为了直观的对比两种控制算法下编队控制系统的控制精度,分别取x轴方向、y轴方向、航向角、线速度及角速度的均方根误差Avex、Avey、Ave、Avev、Avew数值进行对比,如表1所示。 表1 各状态变量跟踪误差对比 由图9和图10可知:在相同预设误差范围条件下,相对位姿跟踪状态量均保持在预设误差范围内,A 算法轨迹跟踪误差范围为(−2 × 10−8, 5 × 10−8) m,B 算法轨迹跟踪误差范围为(5 × 10−4, 5 × 10−3) m,与B算法相比,A算法轨迹跟踪误差范围极大的减小,控制精度得到极大的提高。由图11~图14及表1可得:与B算法控制效果相比,A算法在x轴方向、航向角跟踪误差精度都提高了5个数量级,在y轴方向的位置跟踪误差及角速度跟踪误差精度提高了4个数量级,线速度控制精度提高了10个数量级。此外,实验结果显示,A算法控制系统的平均跟踪误差收敛时间为 4.1 s,B 算法为 3.87 s,即 A 算法下的控制系统响应速度延迟了5.9%,这是因为模糊控制系统增益调整导致的时间轻微延缓。但与B算法图中跟踪曲线相比,A算法图中跟踪曲线更光滑,且无抖振现象产生,达到了稳定的编队的目的。 为进一步对比分析,设计3种指标函数对两种算法的编队控制性能进行整体评价。 1) 控制系统指令跟踪准确率函数 定义控制系统指令跟踪准确率函数为每个控制系统指令输入量的最大绝对跟踪误差与最小绝对跟踪误差的差值的平均值。 式中:m为每个机器人的指令输入量个数;n为参与编队的机器人个数;eicmax、eicmin分别为理想输入量跟踪最大误差和最小误差。函数值越小,控制系统性能越好。 2) 队形紧凑密度函数 定义队形紧凑密度函数为编队中各个机器人到队形几何中心距离之和的倒数,几何中心为O(x0,y0)。函数值越大,队形越紧凑。 式中第i个机器人位置坐标为 (xi,yi)。 3) 队形保持函数 定义队形保持函数为各机器人与各自期望位置的均方根误差,即 式中:m为测量次数; (xij,yij)、 (xdj,ydj)分别为机器人i在j时刻的实际位置坐标和理想位置坐标。函数值越小,队形保持越好。 由式(22)~式(24)计算可得编队整体评价,如表2所示。 表2 队形整体评价对比 由表2可知,在控制系统指令跟踪准确率方面,A算法比B算法跟踪精度大约提高了4个数量级,即对外界干扰的克服能力更强;在队形紧凑性方面,A算法比B算法提高了6.94%,队形相对来说更加紧凑,不容易掉队;在队形保持方面,A算法比B算法提高了3个数量级,队形保持度明显更优。 综上,在预设条件约束下,基于模糊增益调整的滑模编队控制算法实现了任意队形的稳定编队,与现有控制法相比,系统响应速度大致相同,但超调量大大降低,能够有效克服外界干扰保持紧凑的队形,极大的提高了轨迹跟踪控制精度,且跟踪误差收敛于原点附近的极小范围内,保证了瞬态和稳态的良好运动性能,表现出更优越的控制效果。 1)提出一种在双曲正切型函数的约束下模糊增益调整的滑模控制器,用以实现机器人以任意队形高精度稳定的编队控制。 2)从跟踪误差方面分析,该算法与tan型障碍李亚普诺夫算法控制效果相比,跟踪误差范围极大的减小,控制精度大为提高,在x轴方向、y轴方向、航向角以及角速度跟踪误差精度至少提高了4个数量级,尤其线速度控制精度提高了10个数量级,在响应速度轻微延迟情况下,跟踪曲线更为光滑,且无抖振现象产生,实现了稳定编队。 3)从队形整体评价分析,该算法与tan型障碍李亚普诺夫算法相比,跟踪准确率精度提高了4个数量级,对外界干扰的克服能力更强;队形紧凑性方面提高了6.94%,队形更加紧凑;队形保持精度提高了3个数量级,队形保持度更优。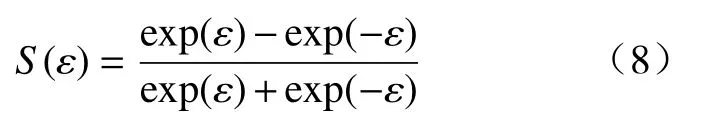
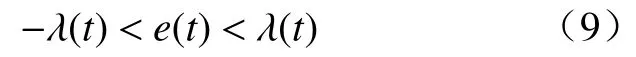
2.3 模糊滑模控制率设计
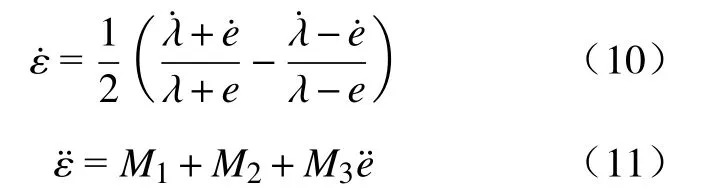
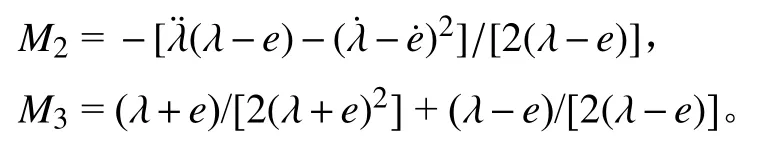
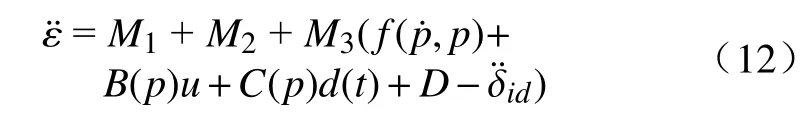
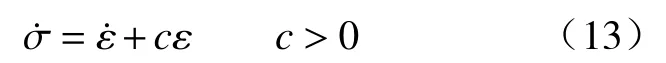
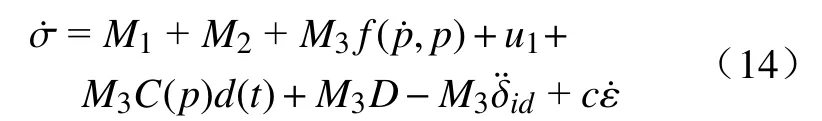
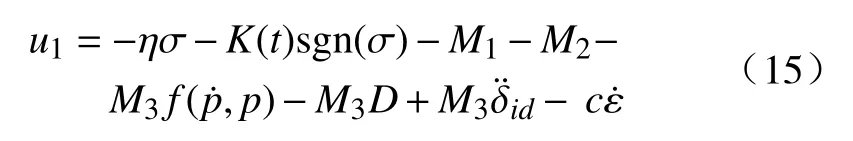


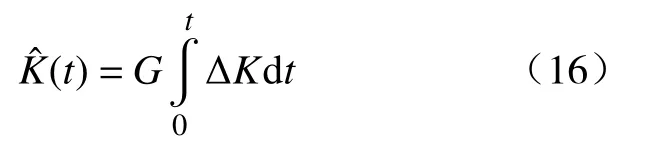
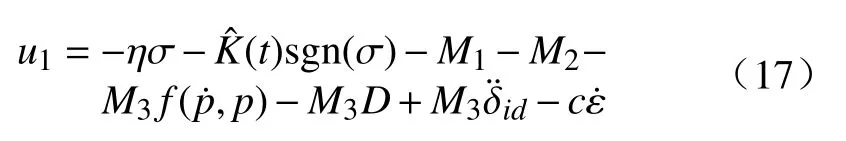

2.4 控制系统稳定性证明

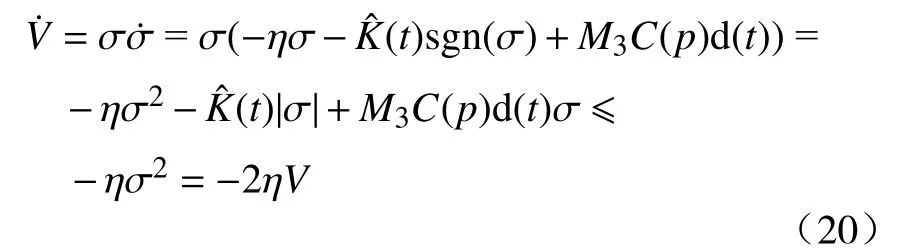
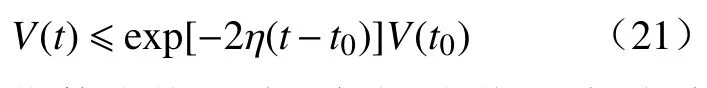
3 仿真试验验证与分析




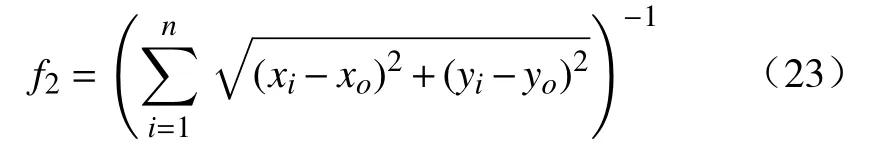


4 结论

