深度对抗迁移学习的故障诊断方法研究

岳帅旭，雷文平，薛阳，王前江，徐向阳

（郑州大学 振动工程研究所，郑州 450001）

随着工业互联网的发展，机械故障诊断已经进入“大数据时代”[1]。我们可以利用大量数据构建深度学习模型应用于机械故障诊断中。但深度学习应用于工程实际的故障诊断存在一个最大的困难是：现场数据样本稀缺，特别是有标签的故障样本稀缺。由此引入迁移学习[2]。

康守强等[3]提出基于特征迁移学习的诊断方法，引入半监督迁移成分分析法，将不同工况的样本特征共同映射到一个共享再生核Hilbert空间，使其在变工况下滚动轴承多状态分类中具有更高准确率。Tong等[4]提出一种特征转移学习（DAFTL）的自适应学习方法，通过基于公共空间中的最大平均差异和域不变聚类来完善伪测试标签，同时减少训练数据和测试数据之间的边际和条件分布，用于训练数据和测试数据的可传递特征表示；雷亚国等[5]提出一种通过构建领域共享的深度残差网络，然后在深度残差网络的训练过程中施加领域适配正则项约束, 形成深度迁移诊断模型。张根保等[6]提出了一种基于迁移学习理论的轴承故障诊断模型，该模型由栈式稀疏自动编码器（SAE）和Softmax函数回归组成，引入高阶KL散度训练域自适应能力，可以从具有大量已知数据的工况迁移到仅有少量数据的相似工况中。然而，以上的研究以减小源域与目标域的域间差异为目的建立诊断模型，域间差异的大小过于依赖度量工具[7]的选择，导致无法最有效提高模型的准确性。

针对上述研究 ，本文提出一种多模态融合深度对 抗 迁 移 学 习 （ Multimodal adversarial adaptive network，MAAN）应用于机械设备故障中，利用神经网络本身来优化算法减小差距。此方法针对试验室可获取大量有标签数据，而实际工况中无法获取大量有标签数据的问题。在模型输入阶段采用时域与频域融合后的数据作为输入，获取故障更为全面的信息。模型训练目标为两个：最大化域分类损失用于对齐源域与目标域之间的边缘概率分布和条件概率分布；最小化源域数据类别预测损失用于准确分类，模型的总体损失为最小化。因此，域分类器与源域故障分类器在训练过程中相互对抗[8-9]实现域分类损失与故障分类损失之间的纳什平衡。从而实现减小源域与目标域分布差异，利用源域分类器识别目标域故障类型，即诊断模型的迁移学习。

1 迁移学习

对抗迁移学习的任务是在试验室条件下获取机械设备的故障数据集，假定试验室有标签的源域为由于实际工况的复杂性，两者数据的产生存在较大的差异。假定实际工况的无标签目标域数据为由于数据产生机制的影响，这两个域的分布不同[10]，即P(xs)≠P(xt)。

但它们的特征空间相同Xs=Xt，假定它们的类别也相同Ys=Yt。因此迁移学习的目标就是利用有标签的数据去学习一个分类器f:xs→yt来预测目标域Dt的标签yt∈Yt，示意图如图1所示。

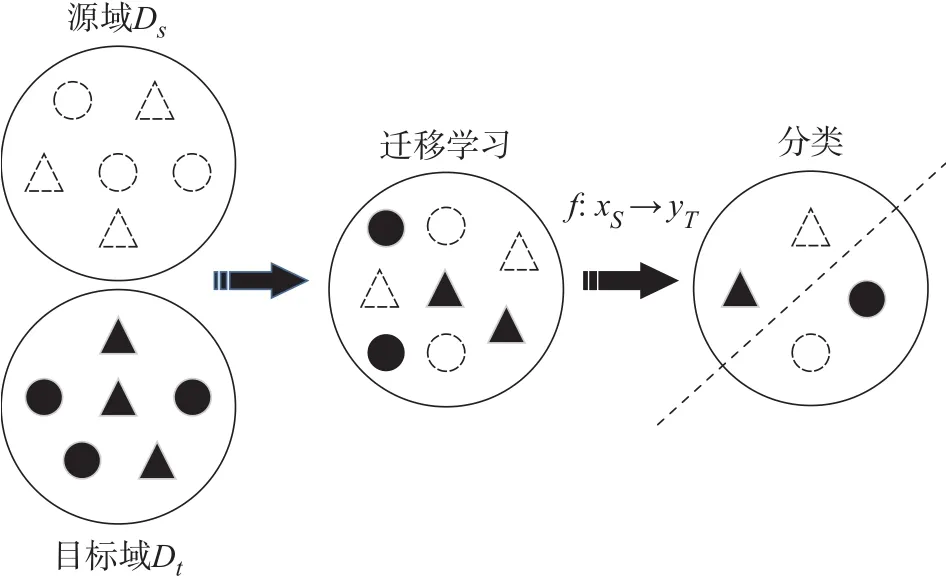
图1 迁移学习示意图

2 对抗迁移学习网络

2.1 模型结构设计

对抗迁移学习（MAAN）模型结构设计如图2所示。数据融合层从时域和频域两个角度融合提取样本的故障数据，频域信号为原始振动信号傅里叶变换获取的有效频谱信号。融合方式采用拼接时域与频域的原始信号，以获取较为全面的故障数据信号作为模型的输入。

图2 MANN 模型结构图

特征提取层设计有一层卷积层和深度残差网络层[11]（Deep residual network，ResNet）构成。第一层卷积层为获取更多的样本故障特征，卷积核尺寸为32，步长 16。深度残差采用 ResNet[2, 2, 2, 2]。特征提取层目标包括两部分：1）提取后续网络完成任务所需要的特征；2）将源域样本和目标域样本进行映射和混合。

分类层由故障分类层、全局域对抗层[12]和局部域类别对抗层[13]组成,它们共享特征提取网络的参数。故障分类层利用一层全连接层对源域样本进行准确分类，实现分类误差的最小化。全局域对抗层由三层全连接层构成，用于对齐源域与目标域之间的边缘分布。局部域类别对抗层由多个三层全连接层构成，用于对齐源域与目标域之间条件概率分布。

在模型训练过程中，假设源域数据分布S(x,y)，目标域分布为T(x,y)。输入信号首先经过特征融合层获取融合后的数据x，x经特征提取层的映射转换为一个D维的特征向量f=RD。然后提取特征会分成多个分支，源域数据和目标域数据对应的特征向量经过域分类层映射获得对应域分类预测结果，同时源域数据特征向量经过Gy(x;θd)得到分类预测的故障标签结果。

2.2 损失函数设计

2.2.1 故障分类损失

故障分类层Gy主要用于训练标签分类器，利用Ds上的监督信息，进行训练网络，其训练目标为交叉熵损失表示为

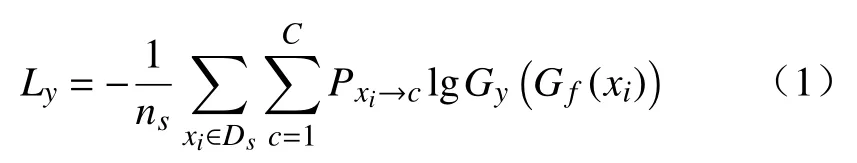
式中：c为类的数量；Pxi→c为xi属 于c类的概率；Gy为标签分类器；Gf为特征提取器。

2.2.2 全局域对抗损失

全局域对抗层对齐源域与目标域之间的边缘分布。在域分类时，源域数据标签是0，目标域数据标签是1。样本特征通过全局域对抗层的损失为

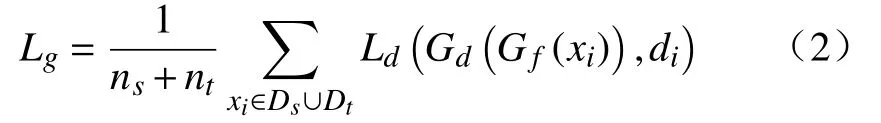
式中：Ld为全局域分类器损失（交叉熵损失）；Gf为特征提取器；di为输入样本的域标签。

2.2.3 局部域类别对抗损失

局部域类别对抗层主要对齐源域与目标域之间的条件分布，局部域类别对抗层在两种分布下，多模结构进行对齐。域分类器Gd分为c个类别的分类器，每个分类器负责匹配源域与目标域相关类别c，标签预测器Gy(xi)对每个样本的输出表示每个样本xi在 类别上相关性，c=1,...,C。局部类别对抗损失可计算为式中：和分别为在类别c上的局部域分类器和交叉熵损失；为输入样本在类别c上的预测概率分布。

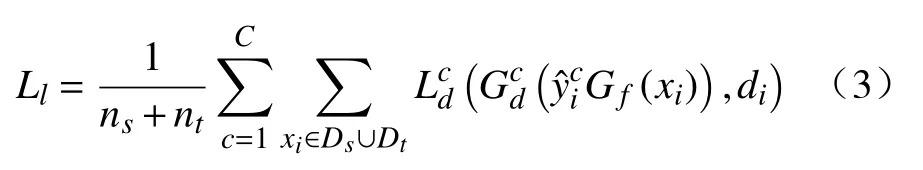
2.2.4 对抗网络的总损失

对抗网络的总损失主要由3部分组成，故障类别损失、全局域对抗损失和局部域类别对抗损失。因此，引入超参数、作为权重平衡参数，则网络的总损失为

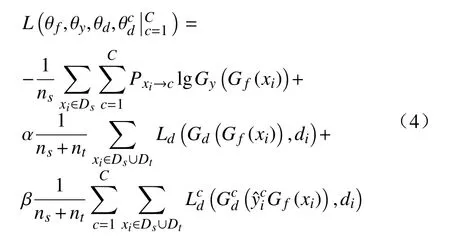
在梯度反转层（GRL）中，使得在域对抗层的反向传播过程中梯度方向自动取反，在前向传播过程中实现恒等变换，相关数学表达式为：

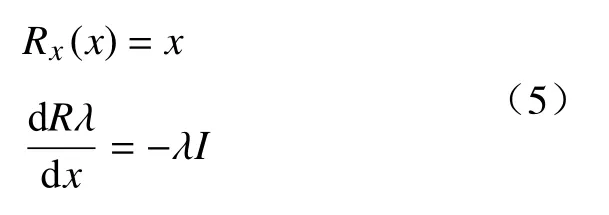
参数 λ并不是固定值，而是动态变化的。其变化表达式为

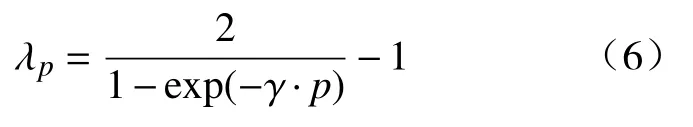
式中：p代表迭代进程相对值，即当前迭代次数与总迭代次数的比率；γ为常数10。

3 试验验证

3.1 数据的来源

试验采用的迁移诊断数据集由XJTU-SU滚动轴承加速度寿命试验数据集和CWRU试验台数据集组成。

1）XJTU-SU数据集是西安交通大学加速度寿命试验台[14]，数据参数如表1所示，试验轴承型号为 LDK UER204 滚动轴承，采用的是 11 kN 径向力下支撑轴承作为试验数据集，转速为2 250 r/min，采样频率为 25.6 kHz。

表1 XJTU-SU 轴承的技术参数和规格信息

2）CWRU轴承数据集是凯斯西储大学轴承试验台。数据参数如表2所示，试验轴承型号为SKF 6205滚动轴承，采样频率为12 kHz。试验负载为0、1、2、3 HP，对应转速为1979、1772、1750、1730 r/min的4种工况下采集振动信号，轴承损伤参数为0.18、0.36、0.5、0.72 mm。

表2 CWRU 轴承的技术参数和规格信息

3.2 试验对比分析

试验数据集样本分为训练集、测试集和验证集，以7∶2∶1的比例进行划分。因试验数据集需求较大，为应对数据集缺少的问题，对数据集重叠采样，扩大样本数量，如图3所示。

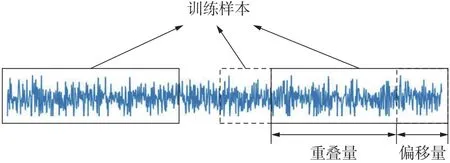
图3 数据重叠采样示意图

试验样本为轴承原始振动信号，采样长度为1024，频域信号获取有效频谱长度400。其中，模型经多次试验分析，学习率lr=0.01，超参数 α =0.05，β=0.25，模型准确率最高。为模拟实际工况的环境，试验对目标数据进行加噪处理，模拟实际工况的噪声影响。加噪信号为高斯白噪声，如图4所示。

图4 30 dB 高斯白噪声加噪示意图

3.2.1 数据融合层试验

试验验证时域、频域和融合后的数据对模型迁移学习的影响。数据集如表3所示，数据输入由模型第一层卷积输入，针对迁移诊断任务A→B进行试验验证数据类型对迁移效果的影响。

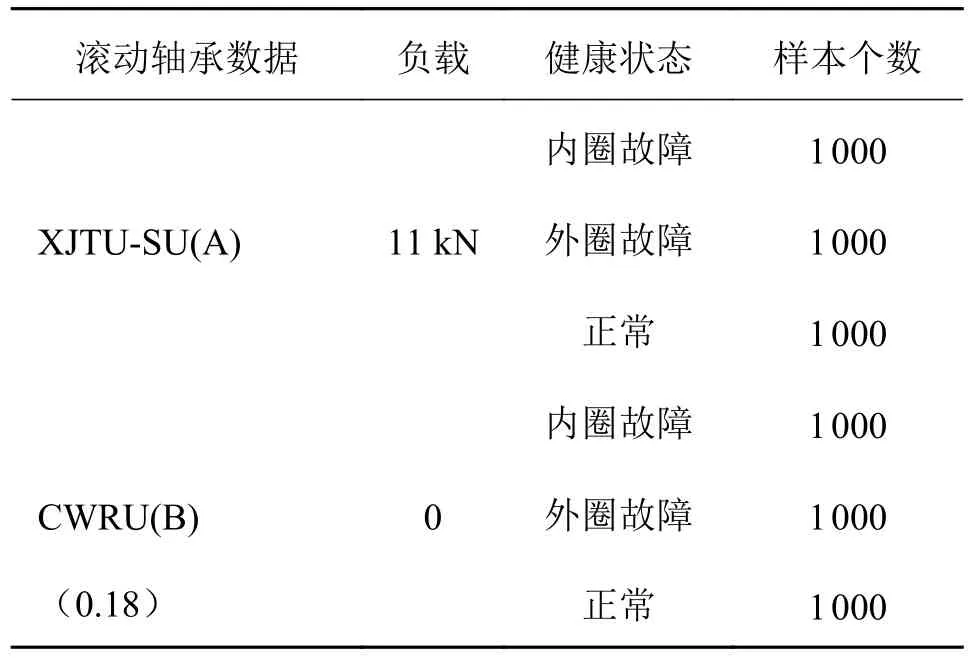
表3 轴承数据集

试验结果如图5所示，准确率为多次训练取平均值。当时域信号作为模型输入时，模型迁移准确率为85%；频域信号作为模型输入时，模型迁移准确率为87%；融合后的数据作为输入为时为95%，有较高的迁移准确率。因此，融合后的数据作为模型输入，能更全面的获取故障信息，有效提高模型迁移效果。

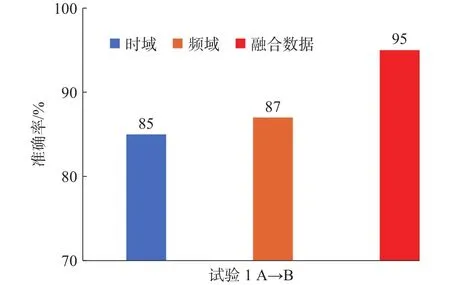
图5 时域、频域、融合后的数据迁移准确率对比图

3.2.2 不同数据源迁移学习验证

试验分为两组进行，第一组试验以数据集A→B进行模型的验证；第二组以B→A进行模型的验证（数据集见表3）。为模拟实际工况的环境，对目标域数据加SNR = 30 dB的高斯白噪声。试验结果如图6所示，图中模型的准确率取20次训练的平均值作为参考。针对迁移诊断任务A→B，对抗迁移学习的准确率为95%，标准差为3%。对于任务B→A，对抗迁移学习的准确率为82%，标准差为4%。由此可知，所提出方法（MAAN），在一定条件下可以利用试验室环境下积累的故障诊断知识，迁移应用于实际工况的健康状态诊断。

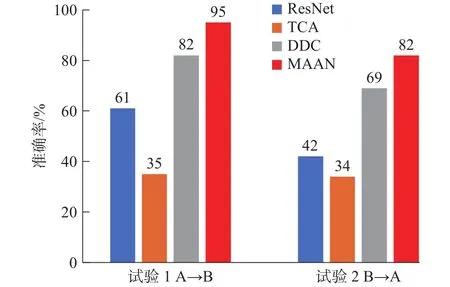
图6 不同数据源迁移诊断结果对比图

为进一步说明提出方法的优势，试验对比分析ResNet网络本身迁移学习能力、TCA迁移学习[15]能力、DDC迁移学习[16]能力。

1）ResNet。该方法与提出方法具有相同的结构参数，但缺少迁移故障特征域对抗层。针对迁移诊断任务A→B，该方法对数据集B的迁移诊断正确率为61%，对于任务B→A，迁移诊断准确率为42%，由于不同数据源数据分布存在差异，对于目标数据的识别精度不高。

2）TCA。TCA的方法是将两个领域的数据一起映射到一个高维的再生核希尔伯特空间。在此空间中，最小化源和目标的数据距离，同时最大程度地保留它们各自的内部属性。针对迁移诊断任务A→B该方法对数据集B的迁移诊断正确率为35%，对于任务B→A，迁移诊断准确率为34%。TCA相比较普通ResNet有更低的迁移学习能力，究其原因TCA缺少深度迁移学习特征能力。

3）DDC。DDC的方法是通过在源域与目标域之间添加一层自适应层，让网络在学习如何分类的同时减小源域与目标域之间的分布差异，从而实现域的自适应学习。针对迁移诊断任务A→B该方法对数据集B的迁移诊断准确率为82%，对于任务B→A，迁移诊断准确率为69%。因此，提出的方法有更高的准确率，一方面所提方法在特征提取方面获取故障时域、频域更为全面的故障信息，另一方面加入条件概率分布的适配过程。

3.2.3 不同工况下迁移学习试验

进一步验证所提方法针对不同工况下的迁移学习能力，对比3组不同工况下的迁移学习验证。试验数据集如表4所示，试验以0作为源数据，分别向 1 HP、2 HP、3 HP 工况下进行迁移学习，验证不同工况下的迁移准确率。

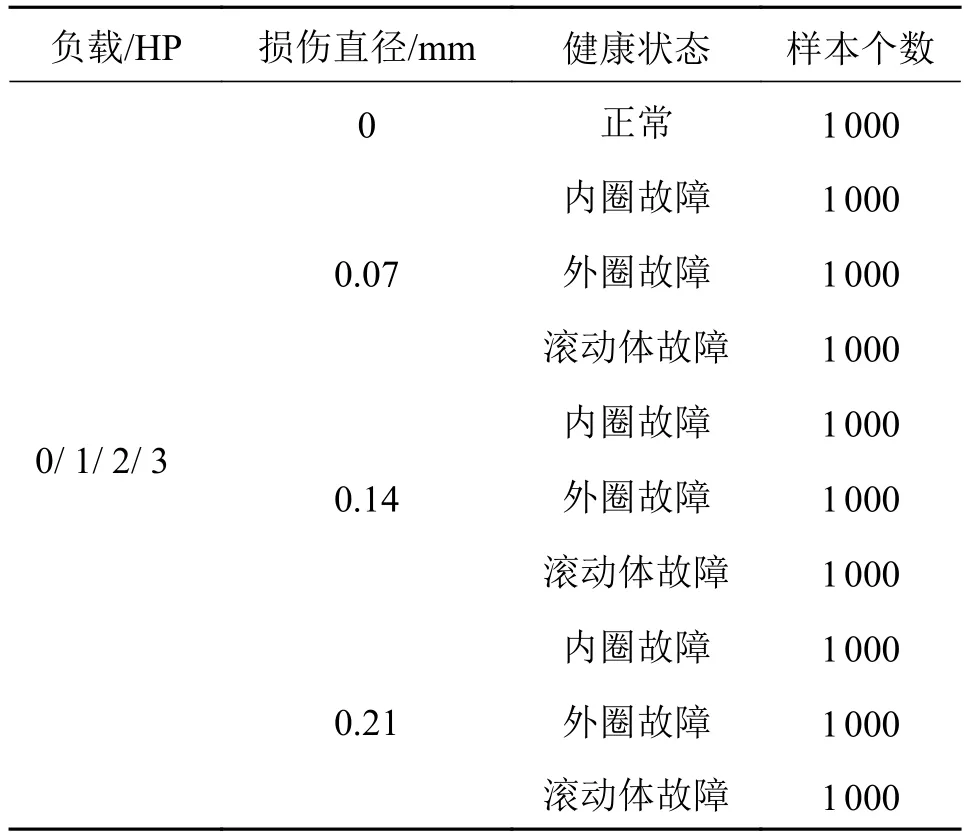
表4 CWRU 轴承故障数据集

为模拟实际工况的环境，对目标域数据1 HP、2 HP、3 HP 的轴承数据加 SNR = 35 dB 高斯白噪声模拟实际工况下的噪声影响。试验结果如图7所示，图中模型的准确率取20次训练的平均值作为参考。针对第一组试验0 →1 HP，对抗迁移学习的准确率 77%，标准差为 4%；第二组试验 0 →2 HP试验，对抗迁移学习的准确率为80%，标准差为3%；第二组试验0 →3 HP，对抗迁移学习的准确率为78%，标准差为4%。

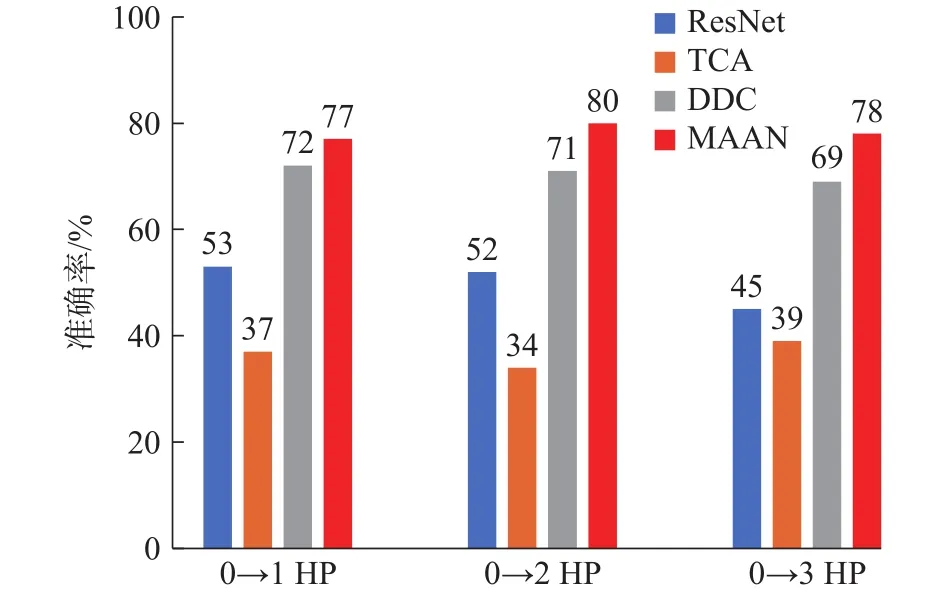
图7 不同负载下迁移诊断结果对比图

试验同样对比分析所构建的ResNet网络本身迁移学习能力、TCA迁移学习能力、DDC迁移学习能力和所提方法（MAAN）的迁移学习能力。由此可知，本文所提方法在不同工况下也可以较好的实现迁移学习。

3.3 试验结果分析

通过验证不同数据源和不同工况的迁移效果来验证所提方法的有效性。同时对比析ResNet、TCA和深度迁移DDC，试验证明所提出的深度对抗迁移学习（MAAN）较其他方法有更高的分类精度。

为了能更直观分析提出方法的有效性，采用t-SNE算法将源域、目标域数据由模型特征提取层提取的特征降维至二维平面进行分析。针对迁移诊断任务A→B，如图8所示。由数据分布情况可知，对抗迁移学习能够减少源域与目标域间的数据分布差异，比较直观解释所提方法的有效性。

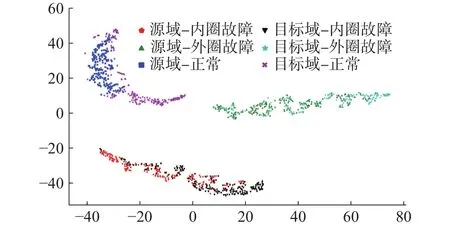
图8 t-SNE源域、目标域模型提取特征降维分布图

4 结论

本文以机械设备故障智能诊断的实际工程应用为目标，针对机械设备故障在不同载荷以及复杂工况下所体现出来的非平稳性、非线性等特性，建立对抗迁移学习诊断模型。以试验室条件下机械设备故障样本空间向工程实际运行样本空间进行迁移学习，进而建立从试验室样本空间向工程实际样本空间的迁移诊断模型，总结本文有以下主要结论：

1）在数据处理和特征提取方面。利用同源信息的不同方面特征，获取更全面的故障信息。同时为解决数据量缺少问题，利用重叠采样扩大训练样本数量，以获取更多有效数据训练模型。

2）构建基于对抗迁移学习诊断模型。利用第一层卷积与多级ResNet网络作为特征提取层，为对抗层提取更为有效的特征和多级参数共享层，同时对抗层对齐边缘分布和条件概率分布，保证模型迁移的准确性。