基于超图正则化非负Tucker 分解的图像聚类算法

陈璐瑶，刘奇龙，许云霞，陈 震

（贵州师范大学数学科学学院，贵阳 550025）

0 概述

基于矩阵分解的数据处理方法近年来在计算机视觉、模式识别、信号处理、生物医学工程和图像工程等［1-3］研究领域中得到了成功的应用，如奇异值分解、主成分分析、独立成分分析、线性判别分析等方法。这些方法都是将原始矩阵近似分解为多个低秩矩阵的乘积［4］。分解的因子矩阵的元素可能是正数也可能是负数，但在实际应用问题中负值元素往往没有意义或无法解释，如图像数据的像素值不可能是负值，文档的数目及词汇的个数也不可能是负值。鉴于此，文献［5］提出一种新的矩阵分解方法——非负矩阵分解（Nonnegative Matrix Factorization，NMF），与传统的矩阵分解方法相比，非负矩阵分解所得结果均为非负值，这使得非负矩阵分解在实际问题中得到了广泛应用。文献［6］提出已有的非负矩阵分解方法通常是将二维的图像变为一维向量处理，这种做法破坏了图像像素点之间的几何结构关系，在数据降维和特征提取过程中容易导致信息丢失、维数灾难和小样例问题，文献［7］提出张量表示能在一定程度上避免上述问题。张量是矩阵和向量的高阶推广，其中0 阶张量是标量、1 阶张量是向量、2 阶张量是矩阵。张量分解的两种经典模型为PARAFAC 分解和Tucker 分解［8-10］。PARAFAC 分解是将一个N阶张量分解为若干个秩一张量和的形式；Tucker 分解是将原张量分解成核张量和因子矩阵乘积的形式。文献［11］提出在非负性约束下，Tucker 分解可以像矩阵分解一样提取基于局部特征的表示。因此，非负Tucker 分解（Nonnegative Tucker Decomposition，NTD）是处理非负张量数据的一种常用方法。

文献［12-14］研究数据之间的几何结构，流形学习能够发现嵌入在高维数据空间中观测数据的低维本质结构，以取得更好的低维表示［15］。目前已有一些研究将流形学习理论与非负张量分解理论结合。例如，文献［16］考虑到图像空间的流形结构，将局部线性嵌入正则化项添加到非负平行因子分析（NPARAFAC）模型，研究了邻域保持的非负张量分解方法。另外，文献［17］提出拉普拉斯正则化非负张量分解方法（Laplace Regularized Nonnegative Tensor Decomposition，LRNTD）并用于图像聚类。在每种模式下，NPARAFAC通常比NTD 需要更多的分量［18］，导致NPARAFAC 的数据表示效果不如NTD。传统的Tucker 分解只涉及属性信息，而没有考虑图像之间的成对相似信息。文献［19］考虑属性信息与图像间局部表示的相似程度，提出一种图拉普拉斯Tucker分解（Graph Laplace Tucker Decomposition，GLTD）方法。文献［20］将流形正则化项引入非负Tucker 分解中，提出一种流形正则化非负Tucker 分解（Manifold Regularized Nonnegative Tucker Decomposition，MRNTD）方法。文献［21］在低维表示的前提下，为了同时保持内部的多线性结构和几何信息，将图正则化引入到非负Tucker分解中，提出一种图正则化的非负Tucker 分解（Graph regularized Nonnegative Tucker Decomposition，GNTD）方法。

然而上述研究只考虑到了样本间的成对关系，忽略了样本间的高阶关系［22-24］，文献［25-27］则利用超图可以解决这一不足。本文结合超图学习［22］和NTD 算法，提出一种基于超图正则化非负Tucker 分解算法（HyperGraph Regularized Nonnegative Tucker Decomposition，HGNTD）。利用K-最邻近（K-Nearest Neighbor，KNN）方法建立超图，将超图正则项添加到非负Tucker 分解中，并基于交替非负最小二乘法（Alternating Nonnegative Least Squares，ANLS），设计超图正则化非负Tucker 分解算法（HGNTD）求解模型。

1 相关工作

1.1 非负Tucker 分解

张量分解有两种经典模型：PARAFAC 分解［8］和Tucker 分解［9］。这两种模型都是矩阵奇异值分解的高阶推广，也可看作是主成分分析（PCA）的高阶形式，且前者是后者的一种特例。

NTD 可以看作是NMF 的多线性推广，NTD 的矩阵形式（式（1））和NMF 之间的一个最大的区别是前者的基矩阵是核张量与因子矩阵从模-1 到模-(N-1)的乘积，这有利于改善基矩阵的稀疏性。

1.2 超图学习

超图是普通图的推广，在普通图中，一个数据对象表示一个顶点，两个顶点之间的边用来描绘顶点之间的关系。超图中的超边连接3 个或者更多的顶点可以更好地表示数据的高维信息，超图已经广泛应用于分类、聚类中。下文简单地介绍超图的一些基本理论［22，26］：

假 设G=(V,E,W)，其 中V={ν1,ν2,…,νN}是 顶点集，集合V中的每一个元素称为顶点；E={e1,e2,…,eM}是超边集，集合E中的每一个元素称为超边，每条超边是顶点集V的子集；W为超图的权重矩阵，是由超边的权重构成的对角矩阵，其中每条超边e的权重是事先赋的一个正值w(e)。如果以下两个条件成立：ej∉∅,∀j∈1,2,…,M，e1∪e2∪…∪eM=V，则G是定义在集合V上的超图。

超图可使用一个|V| ×|E|的关联矩阵H来表示：

下文用几何图形解释超图，如图1 所示，其对应的顶点与超边的关联矩阵H如表1 所示。

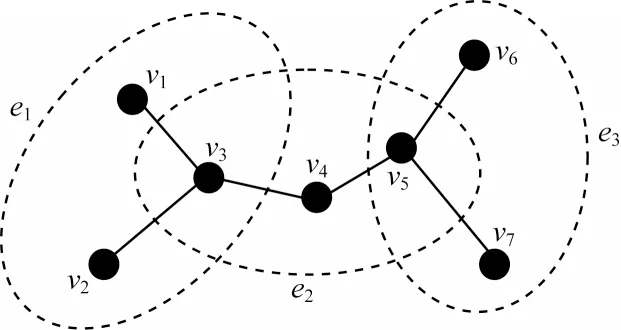
图1 超图G 的几何示意图Fig.1 Geometric schematic diagram of hypergraph G

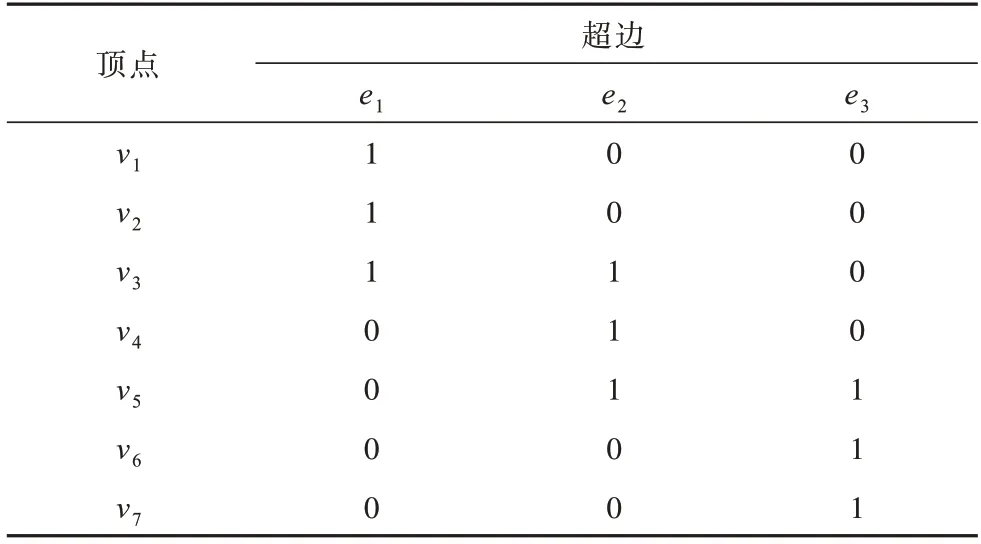
表1 图1 对应的关联矩阵HTable 1 The correlation matrix H corresponding to Fig.1

图1给出一个超图G=(V,E)，实心节点表示为顶点，由椭圆虚线标记的集合表示超边。表1表示为其对应的关联矩阵H，其 中，V={ν1,ν2,…,ν7}，E={e1,e2,e3}，e1={ν1,ν2,ν3}，e2={ν3,ν4,ν5}，e3={ν5,ν6,ν7}。

对于顶点ν∈V，ν所属的超边的权重之和称为ν的阶（或度），记为；对于超边e∈E，e所包含的顶点数称为e的阶（或度），记为δ(e)=|e|。因此：

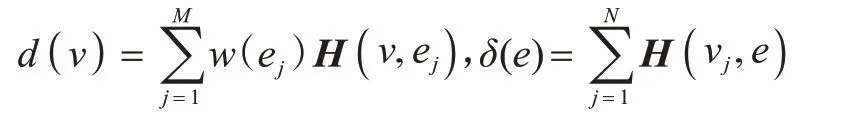
分别用Dν、De、W表示顶点的度、超边的度和超边的权重所形成的对角矩阵，可分别表示为：

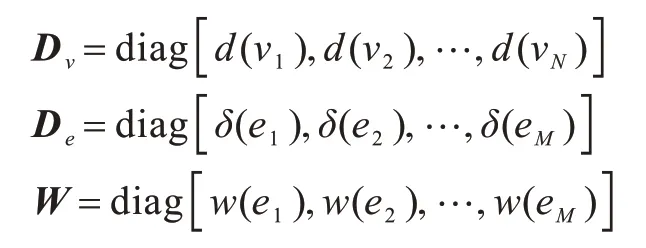
根据文献［22］定义，非标准化超图拉普拉斯矩阵为：

根据超边的定义，允许包含任意数量的顶点。为了方便起见，本文采用在每条超边中包含相同顶点个数的一致超图。

2 超图正则非负Tucker 分解

本文在NTD 和超图学习基础上，提出张量数据超图的构造方法，并将超图的正则化项引入NTD 目标函数中，最后给出求解HGNTD 模型的有效算法。

2.1 超图构造

为了构造超图，可以把数据集中的每个数据点看作超图的顶点，将当前顶点和其最邻近的顶点看作一条超边，通过改变最邻近半径大小定义一组超边。根据超图的不同构造方法可以生成大量超边，使超图更好地描述数据结构。此外，超边权重的选择也很重要，目前最常用的加权方案有3 种：0-1 加权方案，热核（Heat Kernel）加权方案和点乘加权方案。不同的加权方案适用于不同的应用问题，如点乘权重通常适用于文本匹配问题，而热核加权方案常用于处理图像数据。

本文中采用的是热核加权方案，基于给定的图像空间邻域构造一个超图G=(V,E,W)。首先，将Y={y1,y2,…,yN}中的每张图像yi看作超图的一个顶点νi。然后，以每个顶点νi作为空间区域的“质心”节点，并使用K-最邻近（KNN）方法构造相应的超边ei∈E，因此，超图G由构造在不同空间区域上的N个超边组成。基于这些超边，通过式（2）获得关联矩阵最后，使用热核加权方案，赋予每条超边一个正权重［28］，即：

根据上述超图的构造方法，每个顶点与至少一条超边连接，并且每条超边与权重相关联。对角权重矩阵W∈RN×N由下式给出：

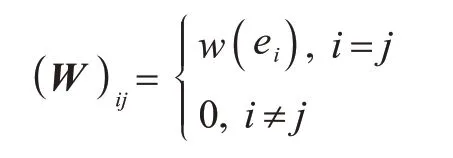
权重矩阵W的权值与两点间的欧氏距离成反比。两个点之间的欧氏距离越小，它们的相似性越高。因此，使用下式来刻画低维数据的光滑性：

其中：Tr(·)表示矩阵的迹；LHyper是式（3）所定义的非标准化超图G的超图拉普拉斯矩阵。

2.2 目标函数

将超图正则化项式（4）加入到原始NTD 的目标函数中，得到HGNTD 目标函数如下：

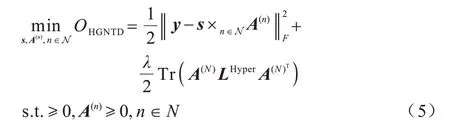
其中：λ是一个非负参数，用于平衡超图正则化项和重构误差项；LHyper是式（3）所定义的非标准化超图G的超图拉普拉斯矩阵。

采用拉格朗日乘子法，并考虑模-n展开形式，然后确定基于式（5）的拉格朗日函数：

可将目标函数重新写为：

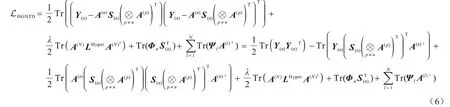
2.3 迭代规则更新

为了求解式（6），采用交替非负最小二乘迭代方法，即每次只更新核心张量或一个因子矩阵，同时固定其他因子矩阵。

2.3.1 因子矩阵A(n)(n≠N)更新

LHGNTD对于A(n),n≠N的偏导数为：

因此，得到以下更新规则：

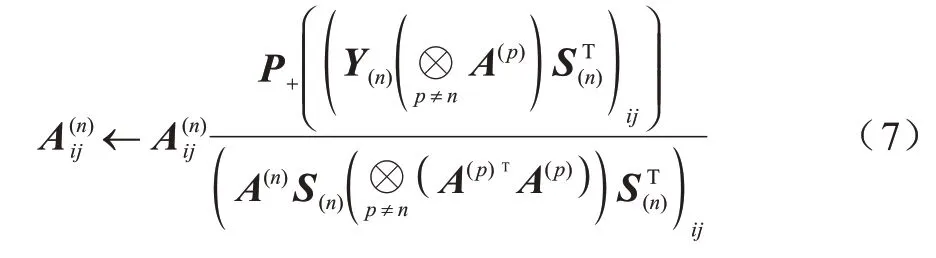
其中：P+(ξ)=max(0,ξ)。

2.3.2 因子矩阵A(N)更新

求LHGNTD关于A(N)的偏导数为：

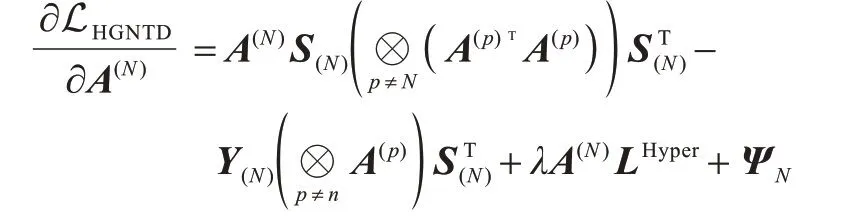
同理，由KKT 条件可以得到以下更新规则：

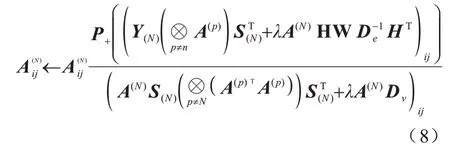
2.3.3 核张量S更新

基于式（5）采用拉格朗日乘子法，并考虑其向量化形式：

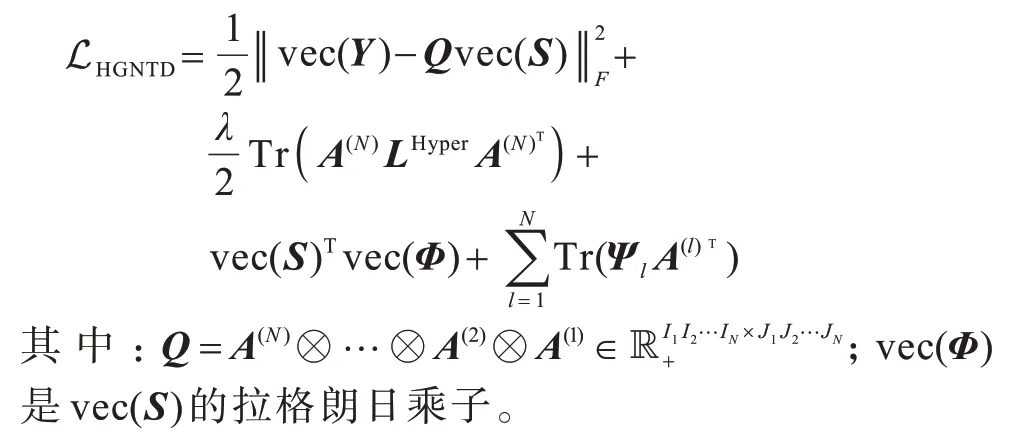
LHGNTD对于vec(S)的偏导数为：

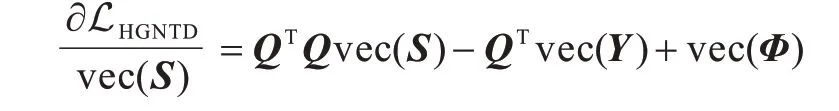
同上，由KKT 条件从而得到以下更新规则：

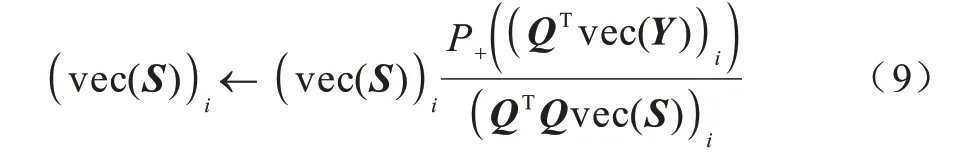
根据以上分析，给出本文算法。

2.4 收敛性分析

定理1若≥0(n∈N),vec(S)≥0，则目标函数式（5）在更新迭代规则式（7）、式（8）和式（9）下是非增的。

为证明该定理，首先引入辅助函数的定义：

定义1若G(x,x′)满足G(x,x)=F(x)，G(x,x′) ≥F()x，则G(x,x′)是F(x)的辅助函数［29］。

引理1若G(x,x′)是F(x)的辅助函数，则F(x)在更新迭代规则［29］：

下是非增的。

证明根据定义1 和更新迭代规则式（10），有：

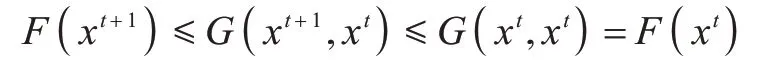
为证明目标函数式（5）在更新规则式（7）下是非增的，先构造关于矩阵A(n)的(i,j)元素的辅助函数。对固定的行列指标(i,j)，令A(n)(x)是通过将矩阵A(n)的(i,j)元素替换为变量x，其余元素不变得到的矩阵函数。

引理2函数：

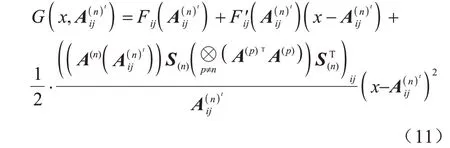
是Fij(x)的辅助函数，其中：

因为：

由定理1 知算法1 是局部收敛的。

3 数值实验

现实中的高维图像数据依据人们能否获得先验信息可以分成两类：一类是可以通过人工标记或可以直接获得先验标签信息的数据；另一类是没有任何类别标签信息的数据。

图像数据分析与处理的方法分为有标签数据的图像分类和无标签数据的图像聚类。它们的区别是：分类是事先定义好类别，类别数不变。分类器需要由人工标注的分类训练语料训练得到，属于有监督学习。而聚类是没有事先规定类别，类别数不确定。聚类不需要人工标注和预先训练分类器，类别在聚类过程中自动生成，属于无监督学习。

本文进行的是无监督的聚类实验，因此无需训练集和测试集，数据集的标签只用于和聚类实验结果进行对比。

为验证本文算法的有效性，选择如下代表性算法进行比较：NMF［5］，GNMF［14］，NTD［18］，GNTD［21］和K-means［30］。本文分别在两个常用公开的数据集Yale 和COIL-100 上进行聚类实验，实验环境为：Matlab 2019a，Intel®Core（TM）i5-7500 CPU@3.40 GHz，3.41 GHz 处理器，8.00 GB 内存，64 位的Win10 操作系统。

3.1 数据描述

实验中所使用数据集如下：

1）Yale。该数据集是由耶鲁大学计算视觉与控制中心创建，包含15 位志愿者，每个采集志愿者包含光照、表情和姿态的变化以及遮挡脸部（不戴眼镜、戴普通眼睛和戴墨镜）状态下的11 张样本，总共有165 幅分辨率为100×100 像素的人脸图像。在实验中，Yale 数据集的所有图像都被调整为32×32 像素的大小，Yale 数据集的部分图片如图2 所示。

图2 Yale 数据集的部分图片Fig.2 Some images of Yale dataset

2）COIL-100。该数据集是哥伦比亚大学采集的（COIL-100）图像数据集。COIL-100 由7 200 幅尺寸为128×128 像素的彩色图像组成，包含100 个目标，每个目标有72 幅不同角度的图像。在实验中，每个彩色图像被调整为大小32×32 像素的灰度图像。COIL-100 数据集的部分图片如图3 所示。

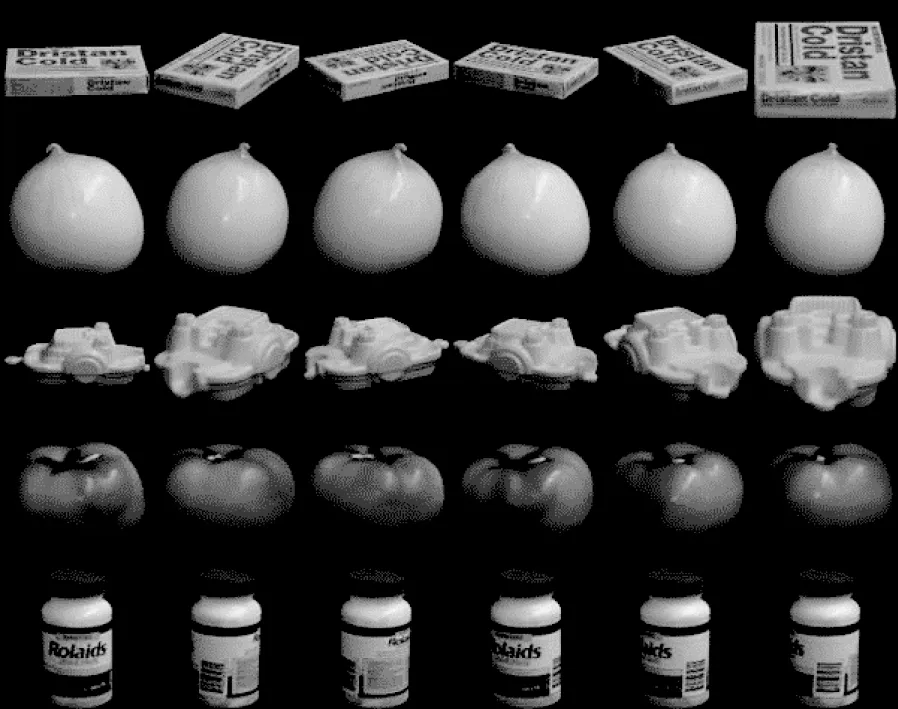
图3 COIL-100 数据集的部分图片Fig.3 Some images of COIL-100 dataset

传统的非负矩阵分解方法将每幅图像向量化后构成相应的1 024×165 和1 024×7 200 的矩阵再做分解，破坏了图像像素几何结构关系。非负张量分解方法直接对32×32×11K和32×32×72K（其中K是簇数）两个张量进行分解，不会破坏图像原有的结构。

3.2 评估指标

为评估聚类效果，使用两个流行的评估指标来评估聚类效果：一种度量标准是聚类准确度（Accuracy）；另一种度量标准是归一化互信息（Normalized Mutual Information，NMI）。

聚类准确度（Accuracy，ACC）定义如下［31］：

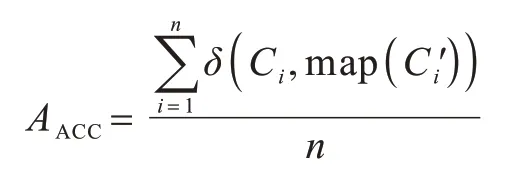
其中：Ci是真实类标签集合是算法得到的聚类标签集合；n是数据样本总数；δ(x,y)是一个kronecker函数，如果x=y，则δ(x,y)=1，否则δ(x,y)=0，并且map)是将每个聚类标签映射到真实类标签集Ci中等效标签的映射函数。为得到最佳映射，通常使用Kuhn-Munkres 算法。

3.3 对比算法与参数设置

为验证本文所提算法的有效性，将HGNTD 分别与NMF［5］、GNMF［14］、NTD［18］、GNTD［21］和k-means［30］算法进行比较，具体参数如下：

1）基于NMF 算法的聚类。目标函数中距离使用Frobenius 范数度量，基矩阵的行数r=10，即低维子空间的维数为r。

2）基于GNMF 算法的聚类。目标函数中距离使用Frobenius 范数度量，并采用热核（Heat Kernel）加权方案，使用k-最邻近方法构造权重矩阵W，其中k=3，图的正则化参数λ取0.5。

3）基于NTD 算法的聚类。目标函数中距离使用Frobenius范数度量，核张量的规模为

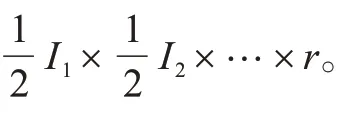
4）基于GNTD 算法的聚类。目标函数中距离使用Frobenius 范数度量，核张量的规模同NTD 算法。采用热核加权方案，GNTD 的其他参数设置与GNMF 的设置相同。

5）基于HGNTD 算法的聚类。目标函数中使用Frobenius 范数度量距离。核张量的规模同NTD 算法。采用热核加权方案，使用k-最邻近方法构造权重矩阵W，其中k=3，超图正则化参数λ=0.5。

3.4 实验与结果分析

具体实验步骤如下：

1）为使实验更具有说服力，对聚类实验配置进行随机化处理，即在不同的类别个数进行聚类实验。每次随机选择数据库中K个类别（COIL-100：K=2，4，…，20；Yale：K=3，5，…，15）。

2）对于k-means 算法，作为一种基线（Baseline）算法，只在原始数据空间中进行聚类。对于NMF、GNMF、NTD、GNTD 和HGNTD 算法，在进行分解后，可以得到各个对比算法对应的低维子空间表示，那么聚类则在这些低维子空间中进行。然后，再将k-means 应用于这些重构表征上进行聚类。

3）计算两个聚类指标精度（ACC）和归一化互信息（NMI）。

4）重复上述步骤20 次，并记录各个聚类算法的平均性能以及上下偏差情况。

Yale 数据集的聚类准确度和归一化互信息的结果如表2、表3 所示，COIL-100 数据集的聚类准确度和归一化互信息的结果如表4、表5 所示，其中粗体为最优值。

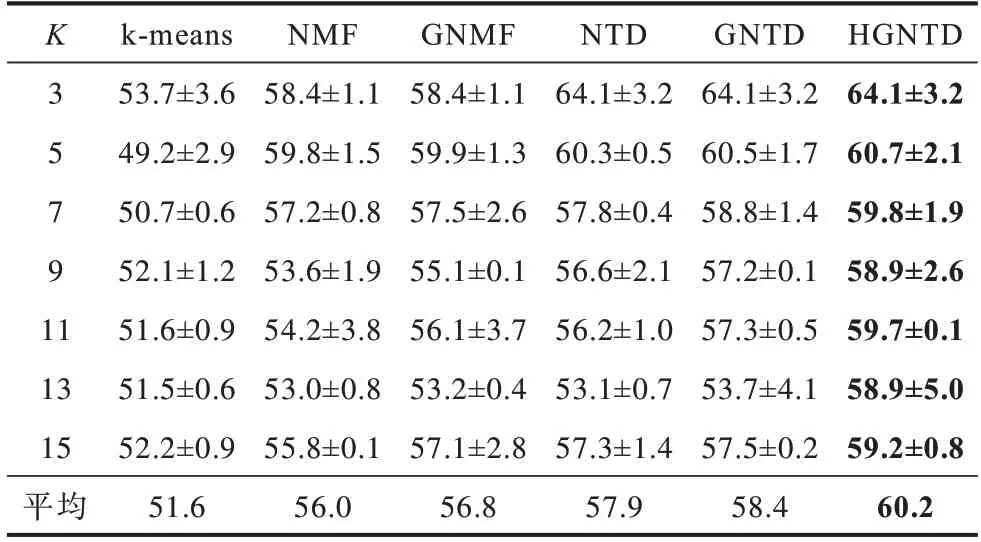
表2 Yale 数据集聚类准确度Table 2 Clustering accuracy of Yale dataset %

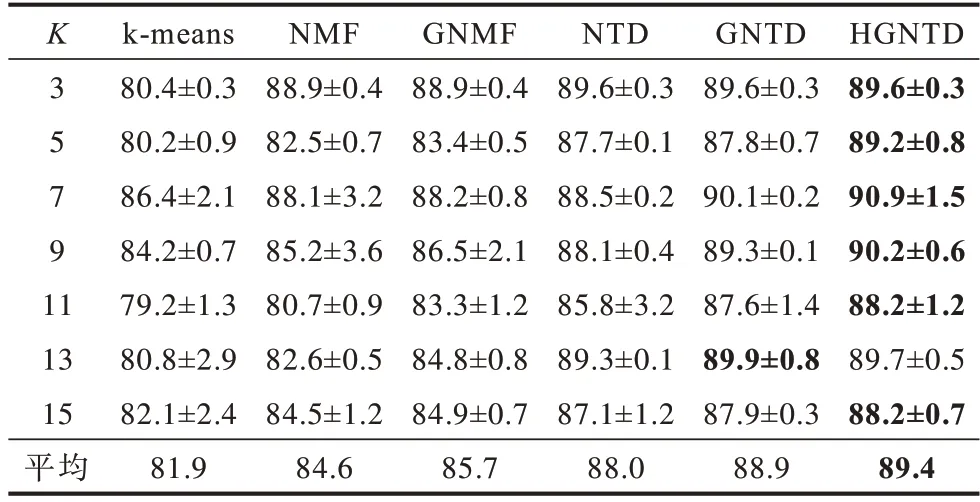
表3 Yale 数据集聚类归一化互信息Table 3 Clustering normalized mutual information of Yale dataset %

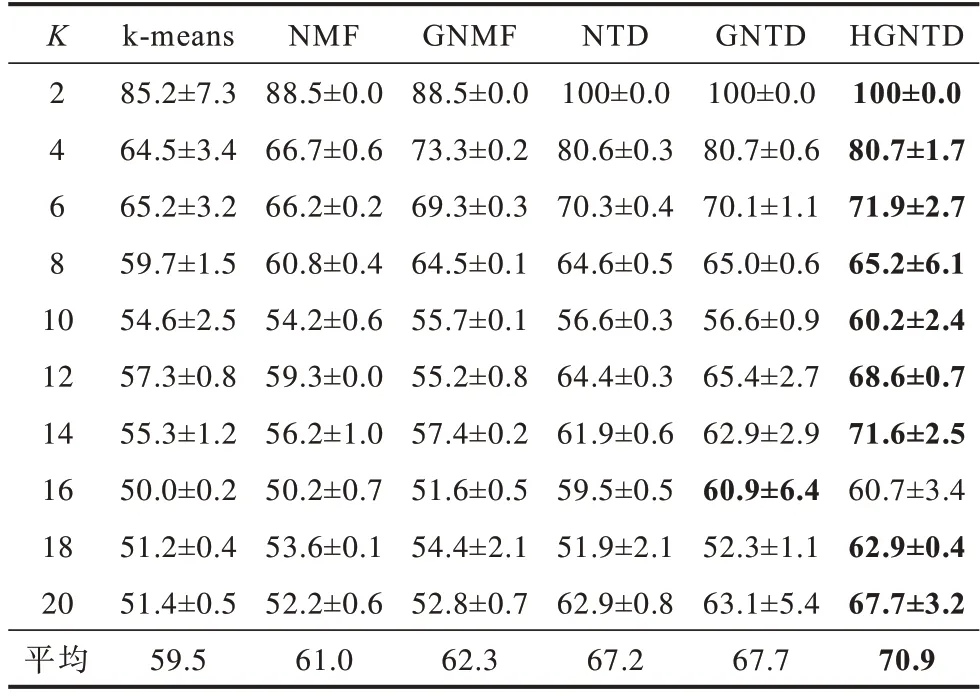
表4 COIL-100 数据集聚类准确度Table 4 Clustering accuracy of COIL-100 dataset %

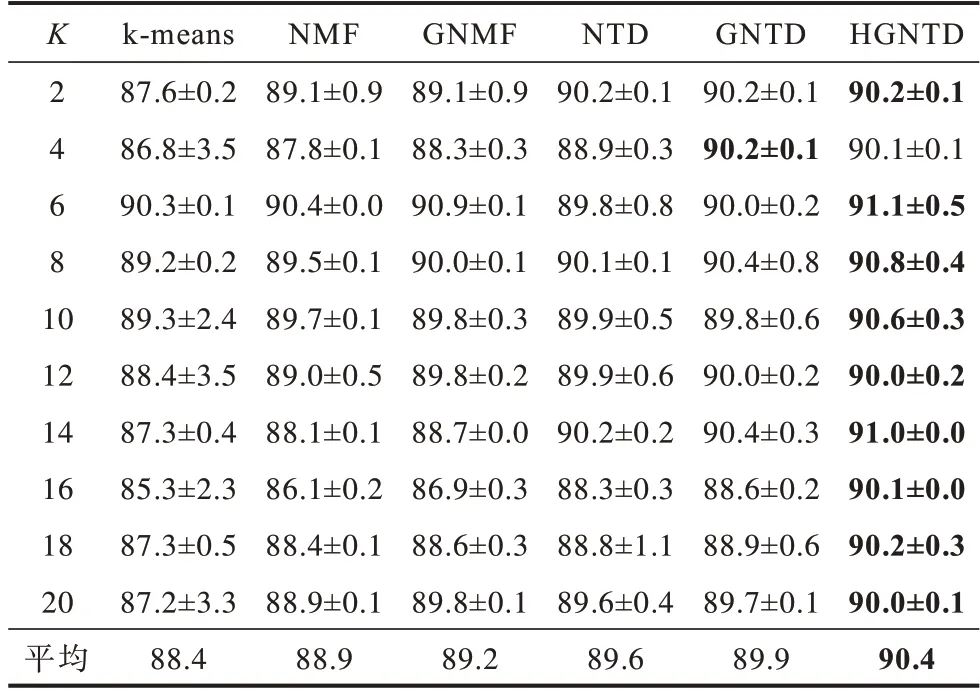
表5 COIL-100 数据集聚类归一化互信息Table 5 Clustering normalized mutual information of COIL-100 dataset %

从表2～表5 可以看出：在保留几何信息和内部结构的情况下，HGNTD 与NMF、GNMF、NTD、GNTD 和k-means 算法相比，聚类性能更好。本文方法比其他方法的聚类准确度提升了8.6～11.4%，归一化互信息提升了2.0～7.5%，这也表明本文提出算法对图像聚类是有效的。

表6、表7 给出Yale 数据集上NMF、GNMF、NTD、GNTD 和HGNTD 算法分别在维数r=4 和r=5下的对比结果，其中粗体为最优值。

表6 Yale 数据集上不同算法的聚类准确度Table 6 Clustering accuracy of different algorithms on Yale dataset %

表7 Yale 数据集上不同算法聚类归一化互信息Table 7 Clustering normalized mutual information of different algorithms on Yale dataset %

由表6、表7 可以看出：在不同维数下，本文算法的聚类结果要比其他算法的聚类结果更好。

图4 所示为NMF、GNMF、NTD、GNTD 和HGNTD 算法在Yale 数据集上的人脸重构效果，分别给出在Yale 数据集上的部分图像，其中，第1 行为原始图像，第2 行～第6 行分别为HGNTD 算法、GNTD算法、GNTD 算法、GNMF 算 法和NMF 算法的样本重构图像。其中，HGNTD 算法的重构图像比其他算法下的样本重构图像更加清晰，复原效果更好。

图4 Yale 数据集部分样本重构图像Fig.4 Reconstructed images from partial samples of Yale dataset

4 结束语

本文提出一种基于超图正则化非负Tucker 分解算法（HGNTD）。利用k-最邻近方法构造超图，将超图正则项添加到非负Tucker 分解中，建立基于超图正则化非负Tucker 分解模型，基于交替非负最小二乘法算法，给出超图正则化非负Tucker 分解算法求解此模型，并证明算法是收敛的。在公开数据集上的实验结果表明，与k-means、NMF、GNMF、NTD、GNTD 等算法相比，该算法具有更好的聚类效果。由于在本文实验中发现图像只需少数基底表示即可，因此下一步将继续对基于稀疏约束的超图正则化非负张量分解算法进行研究，以提高模型的适用性。