V2V 环境下具有组策略防护特性的虚拟交通灯

宋 玮，赵会奋，蔡文钦，周万强

（广东工业大学 计算机学院，广州 510006）

0 概述

交通拥堵是现代城市治理中的一个重要问题。目前缓解交通拥堵的方法［1］包括使用智能交通系统中的交通信号灯和车辆重路由。其中，固定时间周期的交通信号灯无法适应飞速增长的车辆导致的拥堵问题，现有的优化方法将如强化学习、遗传算法、神经网络、模糊逻辑等应用在交通控制领域以减少车辆的整体等待时间、提高交通安全、减少能源消耗等，但这些方法需要大量的历史数据及耗费大量的计算时间。车辆重路由通过为车辆提供可替换的路径来减轻拥堵。文献［2］提出的路径诱导算法所产生的路径可提升车辆准时到达的概率。文献［3］中的基础设施代理使用强化学习更新节点压力，从而获得车辆的最优路径。为了适应交通的动态性，基础设施代理使用组合拍卖调整车辆路由。文献［1］充分总结了车辆重路由和交通信号灯缓解交通拥堵问题的现状，利用数字信息素将两者结合起来，路边设备代理利用车辆代理提供的信息素预测短期交通状态，若有拥堵则进行车辆重路由；交通信号灯代理则利用信息素调整绿灯时长。上述研究均涉及了车辆代理、路边设施代理或交通信号灯代理以及相互之间的信息交换与协作。

另一类研究仅基于车车互联（Vehicle to Vehicle，V2V）与协作，文献［4］提出在V2V 环境下的虚拟交通灯（Virtual Traffic Lights，VTL），不需要依赖任何路边基础设施，仅通过车辆间的直接通信协商路权分配，使用车载显示装置来告知司机交通灯信号，极大节省了修建和维护实体交通信号灯的费用，推广了交通信号灯的使用［5］。但目前的研究均基于一个前提：车车间交互的信息能够被设备感知，且不考虑存在不可被设备感知的信息。文献［6］指出在鼓励拼车的路权分配规则下（车上乘客数越多，车辆通行优先级越高），由司机提供乘客数量，因此司机可以通过谎报车辆满载而获利。文献［7］指出不同的驾驶人对等待时间的估值不同，当驾驶人知道位于他后面的驾驶人会出价使得该车道获得路权，则会谎报他真实的估值。经济学领域提出的策略防护机制是目前用于激励趋利的单个节点偏好进行有益合作的一种有效手段，描述的是参与的节点只有在真实展示其私有信息时所获得的效益最大，常被用作激发节点的真实意图和能力。在合作路口管理中，主要使用第二价格拍卖机制和维克瑞-克拉克-格罗夫斯拍卖机制（Vickrey-Clarke-Groves，VCG）对趋利的单个车辆/司机进行激励，但当节点合谋谎报时则激励失效。

本文依托于车车互联和协作，不考虑使用基础设施代理和信号灯代理。针对在V2V 环境下存在设备不可测量的信息，如车辆/司机对路权的偏好、紧急程度、乘客数量等，本文令车辆合作通过路口，并建模为合作博弈模型，设计一种使用Shapley 值的组策略防护拍卖机制，该机制能够避免车辆虚报私有信息，从而保证车辆评价值的真实性。此外，基于拍卖结果集合中真实的评价值控制虚拟交通灯，并进行路权分配，动态设定绿灯通行的车辆集合，以改变虚拟交通灯中固定绿灯通行阈值的方式。

1 相关工作

1.1 虚拟交通灯

文献［4］指出虚拟交通灯包括3 个部分：1）选举算法选出领导车辆承担实体交通灯的职责；2）领导车辆制定路权分配并发送给车辆；3）当领导车辆离开路口后，领导权按照转移算法转给其他车辆，继续控制交通。但是该文并未给出详细的算法过程。文献［8］在文献［1］的基础上改进了车辆间的消息传播方式并给出了详细的交互过程。文献［5］改变了文献［8］中通过设定绿灯通行车辆数量阈值的方式制定通行时间，提出了独立路口虚拟交通灯的相位算法，并利用每个车道车辆的等待时间、排队链路长度及排队数量这3 个参数制定优先级，节省了等待时间。文献［9］提出的算法可以让通行方向不冲突的车辆同时通行，增加吞吐量，从而减少了车辆的平均行驶时间。除了通过改进交通控制逻辑外，研究分别集中在虚拟交通灯的实施、评价和领导车辆选举算法。文献［10］研究了VTL 在车载系统中用户界面的设计，包括在行驶过程中虚拟交通灯车载界面使用的安全性、用户的接受程度以及对主驾驶任务的负面影响。文献［11］实现了基于Android 手机和WiFi 直连的VTL 的原型系统，并在Carnegie Mellon大学进行测试，研究了消息包的延迟问题，实验结果显示消息包从一台手机传到另一台手机，车辆移动不超过1 m，说明了VTL 依托手机实施的可行性。文献［12］基于文献［1］建立了VTL 的原型系统，并在美国匹兹堡的一个停车场进行了实际的测试，实验结果表明VTL 在无信号灯的路口可以将平均行驶时间减少20%。文献［13］提出了3 个版本的领导车辆选举算法用来减少交互时传递的通信量。文献［14］将VTL 中的领导车辆选举抽象为在无传输失败次数限制的系统中，对一个值或一组值达成一致的问题，即共识问题。

1.2 基于拍卖的合作路口管理

路口是共享资源，从经济学的角度看，道路的使用者对路口的使用具有不同的估值或评价，出价高的将会优先获得路权。研究主要集中在基于拍卖的路口资源预留［6-7，15］和基于拍卖的实体交通信号灯控制［16-18］。这些研究的区别在于：1）采用的拍卖机制不同，有第1 价格拍卖或第2 价格拍卖或VCG 拍卖；2）参与人不同，有车辆或路边设备；3）候选人不同，有车辆或相位或时空隙。这些研究的共同之处是考虑到参与人对行驶时间或等待时间有不同的态度，由此产生对候选实体的不同出价。根据拍卖的特性，只有第2 价格拍卖和VCG 拍卖可以激励参与人真实出价，达到策略防护目的，但是当多个参与人发现可以通过虚假报价合谋获利时，第2 价格拍卖和VCG 拍卖就失效，无法达到组策略防护。

1.3 合作博弈与组策略防护机制

为防止参与人通过虚假报价合谋获利，可采用合作博弈中的机制来维持愿意合作的参与人之间的合作，即维持参与人真实出价的合作，避免参与人合谋并参与虚假报价。合作博弈的正式定义以特征函数的形式给出，即给定一个有限的参与人集合A，合作博弈的特征型是有序数对（A，ν），其中特征函数ν是从2A={S|S⊆A}到实数集RA的映射，即ν：2A→RA，且ν(∅)=0。ν（S）是联盟S中参与人相互合作所对应的效用，可以是得益，也可以是成本。可转移效用博弈（Transferable Utility Games，TU Games）指货币可以被用来在不同的参与人之间转移的效用，满足≤ν(S)，每个参与人都拥有拟线性的效用函数ui，价物（通常为货币）在该效用函数中呈线性关系［19］。对于合作博弈（A，ν），若ν（S）是A的每个联盟S⊆A中参与人相互合作产生的成本，则（A，ν）是成本分摊博弈。向量α∈RA称为成本配置，如果满足下面两个条件则α被认为属于核：1）达到预算平衡，即=ν(A)；2）存在核性质，即对于每一个联盟S⊆A，≤ν(S)。核中的成本配置使任何联盟都没有能力推翻他［20］。成本分摊方案为联盟S指定的成本配置，定义为函数ξ：A×2A↦R，其中S⊆A；而对于每一个i∉S，ξ(i,S)=0。成本分摊方案ξ是交叉单调的，如果对于所有的S,T⊆A和i∈S，则ξ(i,S)≥ξ(i,S∪T)。成本分摊博弈（A，ν）是次模博弈，如果函数ν具有次模性质，即满足式（1）所示条件：

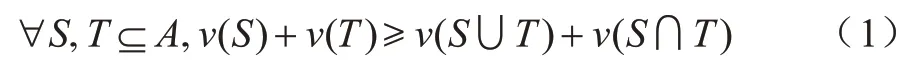
Shapley 值是一种成本分摊方案ξ，可为任一个成本分摊博弈（A，ν）指派唯一的成本配置，计算公式如式（2）所示：

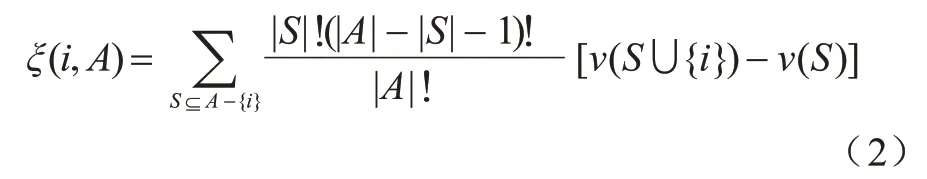
Shapley 值可理解为每个参与人i以随机顺序加入联盟A的期望边际成本。若函数ν具有次模性质，则Shapley 值是成本分摊博弈（A，ν）指派唯一的成本配置并且属于核［23］。这意味着不存在联盟S⊂A有意愿离开A而形成新的联盟。成本分摊机制是一个算法，能够接收多个参与人的出价向量b，并基于b产生一个结果集合Q(b)⊆A和支付函数p(b)∈Rn。

在组策略防护机制中，设S⊆A，b为真实出价向量，b′为策略出价向量。对于每个i∉S，bi=令（Q，p）和(Q',p')为b、b′下的输出。ui(bi,Q,p)为i在b出价向量和（Q，p）输出下的效用。对于每一个S，如果不等式对于每一个i∈S成立，则等号对于每一个i∈S成立。也就是说，不会存在S中每个成员在真实情况下均具有相同效用，同时至少有一个成员能获得更高的效用。这也就意味着这一组成员的策略出价并不会带来更高的效用［21］。

MOULIN 等［23］指出具有交叉单调性质的成本分摊方案ξ可用于设计组策略防护机制，并给出了相关算法和定理。Shapley 值具有交叉单调性质，常被用于组策略防护机制的设计中［21］。

2 具有组策略防护特性的虚拟交通灯

2.1 基本流程

本文遵循文献［1］提出的假设：所有的车辆装备了DSRC 设备；所有车辆共享同一个数字地图；所有车辆具有GPS 来保证全局时间和位置的同步；由现有的无线传输协议提供和解决安全、可靠性和延迟问题。组策略防护特性的虚拟交通灯基本步骤如下：

步骤1所有车辆进入路口区域后广播状态信息给路口区域的其他车辆。状态信息包括车辆的路线、行驶时间、离路口的距离、是否通过路口、对领导车辆的投票等。

步骤2每个车辆根据已获得的信息计算投票，得票最多的是领导车辆。领导车辆的选举使用文献［6］中提出的算法，并增加了一个选举条件：在相同得票的情况下，等待时间最短的为领导车辆。

步骤3一旦确定了领导车辆，领导车辆将控制路口完成以下工作：启动拍卖，使用一个信号队列记录每次拍卖产生的绿灯信号结果。路权分配，从信号队列取出第1 个绿灯信号，发送绿灯消息给相应的车辆。当收到绿灯信号的车辆中最后一辆车离开路口，则领导车辆取出下一个绿灯信号。领导权的转移，当领导车辆离开路口，它会将信号队列传递给新的领导者，新的领导车辆产生过程如步骤2 所示。

步骤4当车辆收到绿灯信号后，使用状态信息说明其正在通过路口。

2.2 车辆合作博弈模型

将车辆合作通过路口，并建模为合作博弈模型（A，ν），合作行为定义为车辆真实展示其不可被设备测量的信息。A是参与合作的车辆集合，令u(A)=1-(1-α)|A|，α是一个车辆参与合作后通过路口的概率，u（A）则是|A|个车辆合作后通过路口的概率。若路口等待的车辆有L辆，当有|A|辆车合作时，期望通过的车辆数量为ν(A)=L(1-(1-α)|A|)。ν（A）具有次模性质，不存在S⊂A有意愿放弃合作并离开A形成新的S，Shapley 值的计算公式如式（3）所示：

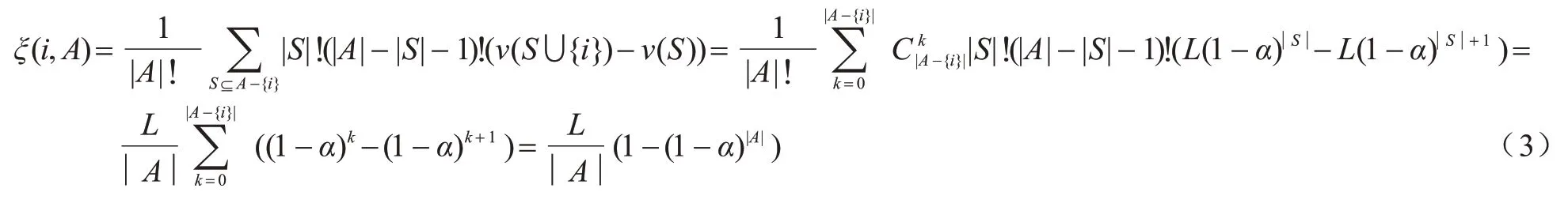
2.3 组策略防护拍卖机制

定义车辆i的效用为wi=uiqi-pi，qi是1 个指示变量，说明车辆i是否入选集合；pi是车辆i的实际支付值；评价值ui描述了车辆不可被设备测量的信息，如主观评价、主观紧急度、乘客数量等。车辆i向领导车辆的出价记为bi，车辆参与到合作中，则显示其真实信息，bi=ui。领导车辆启动拍卖用以确保bi=ui。结合文献［18］提出的机制设计了一个使用Shapley值的组策略防护拍卖机制。设参与拍卖的车辆集合为路口等待的车辆且未参与过拍卖的车辆集合，记为L。Q表示车辆拍卖结果集合，初始时Q=L。领导车辆使用式（3）计算当前Q下的Shapley 值，并判断ξ（i，Q）是否≤bi。如果不等式成立，则领导车辆将选择车辆i进入车辆拍卖结果集合，反之则不选入。调整车辆集合，即Q=｛i|ξ（i，Q）≤bi｝，重复这一过程直到Q不发生变化。最终，Q中的车辆将支付pi=ξ（i，Q）给领导车辆，证明该机制是组策略防护的机制，保证bi=ui且车辆参与合作，并避免车辆/司机形成虚报私有信息的联盟来获取更大的利益。

2.4 路权分配

领导车辆根据固定周期或者当信号队列为空时触发2.3 节中的拍卖机制，依据拍卖结果集合建立绿灯信号，使用信号队列记录每一个绿灯信号。

每个绿灯信号g的结构为（（lg，elg），hg）。lg指获得绿灯信号g的车道号，elg是获得这个绿灯信号g的车道l的总评价值。hg是这个绿灯信号g覆盖的这条车道上的车辆集合。信号队列由多个绿灯信号组成，记为S=｛gi｝，i∈N+。信号队列按照gi中elgi排降序。当信号队列形成后，领导车辆取队首绿灯信号，并通知hgi集合中的车辆为绿灯。当hgi中的最后一辆车驶离路口，领导车辆删除当前队首信号取下一个绿灯信号。

每次拍卖产生新的绿灯信号集合后，领导车辆将其合并到信号队列中，合并算法如下：

算法信号队列合并算法

算法说明：将参与拍卖的车辆集合L依据车道号划分为子集合，计算每个子集合的车道总评价值，形成绿灯信号gi，产生的绿灯信号集合记为S′=｛gi｝。在双向单车道下一次拍卖产生4 个绿灯信号，一个车道对应一个绿灯信号。算法第1 行，如果S中绿灯信号数量为0 或者为1，则直接将S′连接在S后。否则，对于每一个S′中的gi在S中找到具有相同车道的信号gj，将这2 个信号中的车道总评价值相加，车辆集合合并形成新的gj。最后对S按照车道的总评价值排降序。

车道总评价值的计算：如果只以车道中车辆的出价bi计算，会导致等待时间长但bi值小的车辆无法通行，最终使整体的行驶时间变长。用l表示车道，车道l的总评价值记为el值，计算如下：

其中：Ql表示l车道中入选拍卖结果Q的车辆集合；Ll表示参与拍卖的l车道上的车辆集合；wi表示i车辆的等待时间。通过参数控制的方式，使等待时间与bi值具有可比性。式（4）可以保证等待时间过长的车辆尽快离开路口的同时，bi值高的车辆能较快通过。等待时间是设备可测量的值，可通过内置的车载系统获得。

3 实验结果与分析

模拟实验用于验证经济学特性和评价在交通领域内的性能。

3.1 经济学特性的验证

采用matlab 软件验证策略防护特性和组策略防护的特性，参数的设定如下：

1）L是参与一次拍卖的车辆集合，在实际的运行中是变化的。这里主要验证组策略的防护特性，因此采用固定集合L。

2）α是一辆车参与合作后通过路口的概率。

3）β表示驾驶员主观或客观地认为自己的评价值ui为0，比如驾驶员对优先行驶权不感兴趣，只是遵循现有的路况和交通信号行驶。即β表示ui=0 的概率。

4）评价值ui以β为0 为基础进行评估，1-β的概率均匀分布在［1，50］。

5）γ1、γ2控制车辆出价bi，并随机产生0～1 之间的值，如果这个值小于γ1，则车辆虚低报价bi＜ui；如果高于γ2，车辆虚高报价bi＞ui；在其他情况下，车辆报告真实评价值bi=ui。

图1 展现的是当|L|=50 时，Shapley 值随α值以及合作车辆集合规模的变化，选取了车辆规模为1～20的集合。由图1 中可知：当α变小时，Shapley 值变小；当合作车辆集合规模越大时，不同α值的Shapley值的差别越小。因此当集合够大时，如果1 个车辆的bi值能使它进入拍卖结果集合，α变化带来的Shapley 值变化很小，仍然使该车辆进入拍卖结果集合。可见α值不会给拍卖结果集合规模带来很大的影响，但3.3 节中车辆的支付值pi将取决于特定α下的Shapley 值。

图1 不同α 值及合作车辆集合规模下的Shapley 值Fig.1 Shapley value under different α and the scale of cooperative vehicle set

实验1探究α、β和拍卖结果集合间的关系。令|L|=50，ui∈[0,50]，如前所述α对拍卖结果集合影响不大但决定支付值；拍卖结果集合与β值，即ui为0 的车辆个数相关。在相同的拍卖结果集合下α越大说明合作意愿越高，支付值pi越高（见表1，β=0.9），但随着β的减小，不同α下支付的差别越小（表1，β=0.1）。

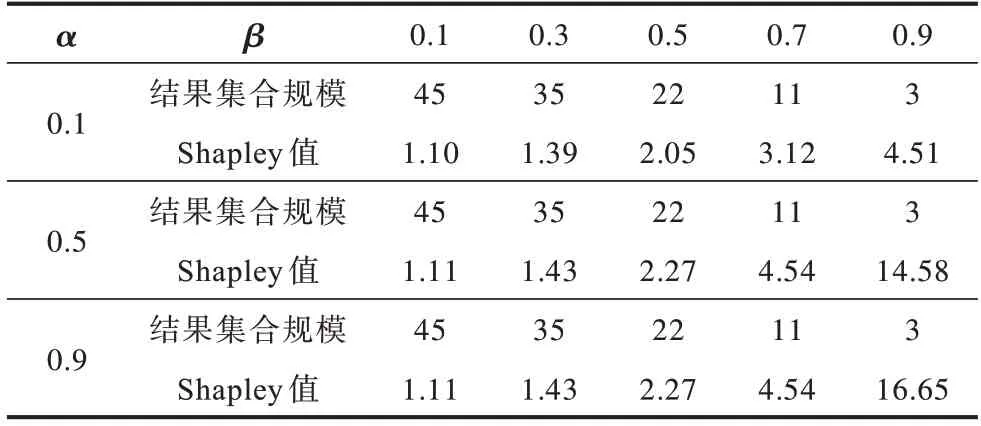
表1 α、β 值与拍卖结果集合间的关系Table 1 Relationship between α，β value and collection auction results

实验2验证策略防护特性，即车辆只有在真实展示其评价值时获得的效用最大。参数设置：|L|=50；α=0.5；β=0.3；γ1=0.4；γ2=0.6；ui∈[0,50]。执 行100 次拍卖机制，每次随机选择一辆车谎报。从图2中可见谎报带来的效用与真实带来的效用间的差值均≤0，这意味着车辆不能从谎报中获得更多的效用，作为理性的车辆只会选择bi=ui。

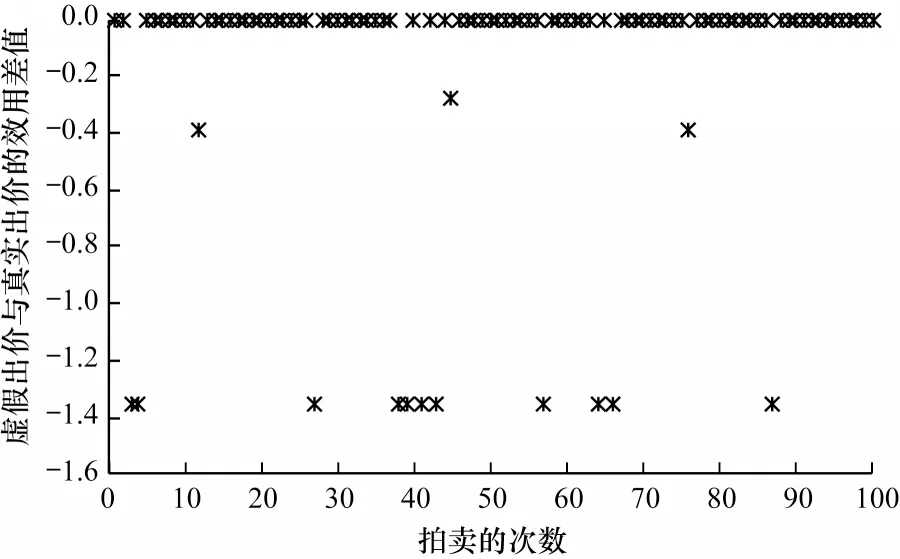
图2 一辆车谎报下的效用差Fig.2 Utility difference when one vehicle misreports

实验3验证组策略防护的特性，即避免车辆形成虚报评价值的联盟来获取更大的利益。执行1次拍卖，随机选择车辆集合谎报，参数设置：|L|=20；α=0.5，β=0.3；γ1=0.3；γ2=0.7；ui∈[0,50]。图3 中有14 辆车合谋谎报，显然有些车辆，如编号为1、6、7、12、13、14 的车辆，并不如在真实场景下获得的效用大，这些车辆将不会停留在合谋集合中，合谋谎报的联盟无法形成。

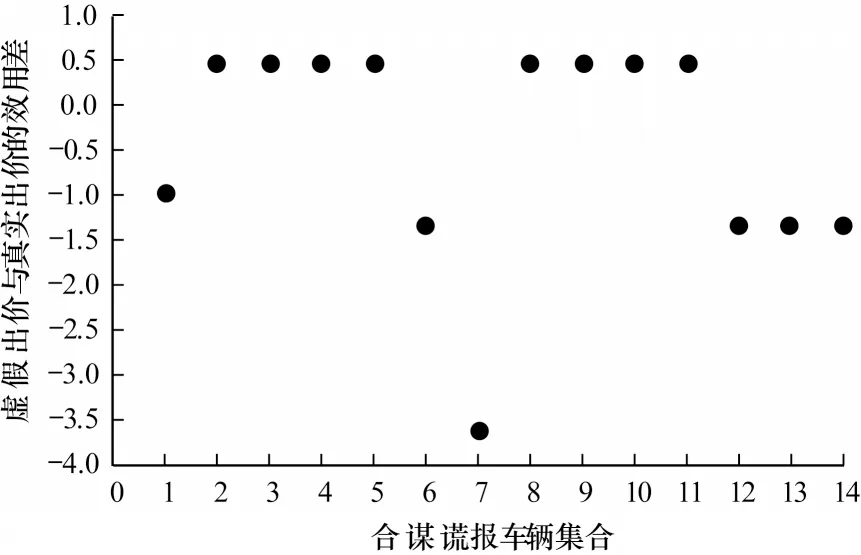
图3 多辆车合谋谎报下的效用差Fig.3 Utility difference when multiple vehicles collude to misreport

3.2 交通领域特性验证

场景参数设置：实验建立在文献［9］搭建的模拟平台上，车辆交互方式、消息格式以及道路和车辆的设置与该模拟平台一致。采用2 种规模的十字路口区域，十字路口由4 条双向单车道交汇而成，车道宽7 m，直行、左转、右转共用1 条道。如图4 所示，规模1的十字路口区域为107 m ×107 m，每条车道长50 m；规模2 路口区域为207 m×207 m，每条车道长100 m。车身长度4.5 m，安全间隙2 m，定义交通密度为每分钟的车辆数（辆/min），运行时车辆的数量由交通密度控制，模拟程序产生30 min 的车辆数据。使用平均行驶时间作为交通领域性能的评价指标，比较文献［6］中实现的VTL 与本文提出的组策略防护的虚拟交通灯（VTLA）。行驶时间为一辆车从进入十字路口区域到离开该区域所花费的时间。

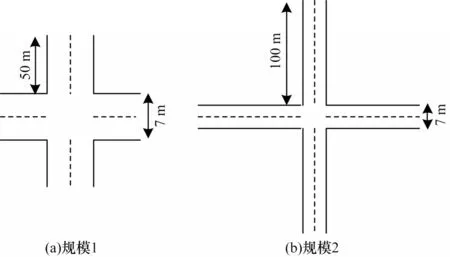
图4 十字路口区域设置Fig.4 Intersection area setting

实验4探究参数VTL_NF_DEFAULT 对VTL平均行驶时间的影响。令文献［6］中实现的VTL 通过设定绿灯通行车辆数量阈值的方式制定通行时间。模拟平台使用参数VTL_NF_DEFAULT 定义该阈值，即1 个车道的首车获得绿灯后，该车道有多少辆车可以跟随首车通过。设交通密度为70；α=0.5；β=0.3；ui∈[0,50]；bi=ui。由 表2 可 知，当VTL_NF_DEFAULT 变大，平均行驶时间则减小，车辆出价的高低与行驶时间无关。

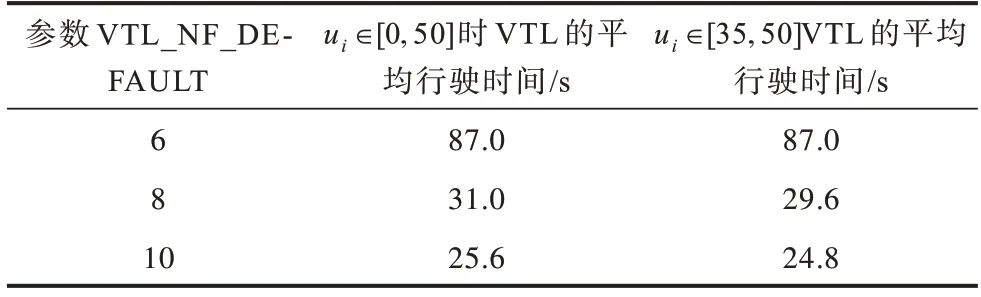
表2 参数VTL_NF_DEFAULT对VTL平均行驶时间的影响Table 2 Effect of VTL_NF_DEFAULT on average duration time of VTL

实验5比较VTL 和VTLA 在不同交通密度下的车辆平均行驶时间（s）和改善度。参数设置：α=0.5；β=0.3；ui∈[0,50]；bi=ui，拍卖周期设置为3 s/次，当信号队列为空时也触发拍卖。VTL 的平均行驶时间受参数VTL_NF_DEFAULT 的影响，因此可以通过计算VTLA 中绿灯信号的平均车辆长度来设置参数VTL_NF_DEFAULT，参数设置如表3 所示。例如，当交通密度为50 时，VTLA 中绿灯信号平均车辆长度为3.8，设置参数VTL_NF_DEFAULT=3，说明VTL 中1 次绿灯通行车辆数量的阈值为4。

表3 参数VTL_NF_DEFAULT 的设置Table 3 Parameter VTL_NF_DEFAULT setting

改善度W的计算公式如式（5）所示：

其 中：dVTL表示VTL 的平均行驶时间；dVTLA表 示VTLA 的平均行驶时间。

如图5 和图6 所示为在规模2 的十字路口中，组策略防护的虚拟交通灯（VTLA）相对于VTL 在平均行驶时间上有较好的改善。当交通密度为30 辆/min～80 辆/min 时，VTLA 的改善度超过30%；对于评价值高的车辆ui∈[35,50]，改善度会更好，如交通密度为50 辆/min 时，VTLA 改善度超过50%。

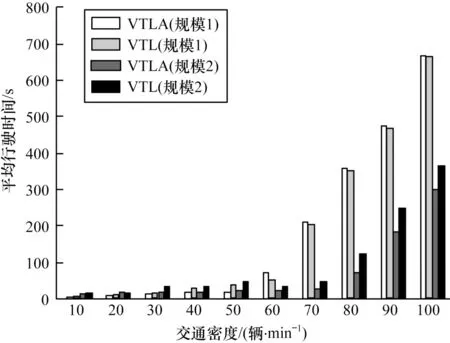
图5 不同交通密度下的平均行驶时间Fig.5 Average travel time under different traffic density

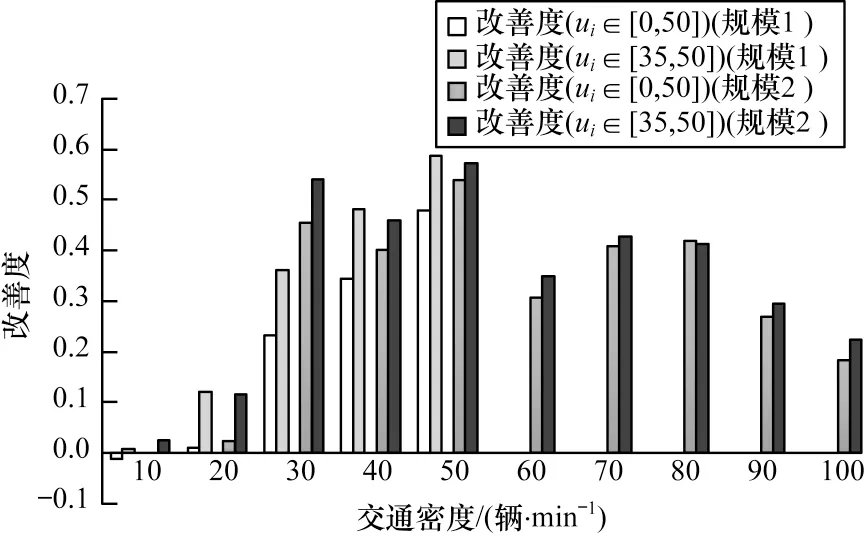
图6 不同交通密度下的平均行驶时间改善度Fig.6 Average travel time improvement under different traffic densities

由图5 中规模1 的十字路口可知，当交通密度为10 辆/min～20 辆/min 时，VTLA 和VTL 的平均行驶时间差别不大；当交通密度为30 辆/min～50 辆/min 时，VTLA 改善度超过50%，对于评价值高的车辆ui∈[35,50]，改善度接近60%（见图6）；但交通密度为60 辆/min～100 辆/min 时，VTLA 和VTL 的平均行驶时间差别不大，并且明显不如规模2 下的性能。原因在于规模1 的十字路口区域只有规模2 的1/2，交通密度为60 辆/min 时，则意味着0.5 h 内有1 800 辆车进入规模1 的区域，相比于0.5 h 内1 800 辆车进入规模2 的区域，明显产生了近似堵车的效果，所以VTLA 和VTL 性能相似。因此，图6 不再展现规模1的十字路口中交通密度在60 辆/min 以上的改善度。

改善度D的计算式如式（6）所示：

其中：d1表示所有车辆（ui∈［0，50］）的平均行驶时间；d2表示评价值ui∈［35，50］的车辆平均行驶时间。

图7 比较的是两种策略中评价值高的车辆，即评价值为ui∈[35,50]，相对所有车辆的平均行驶时间的改善度。

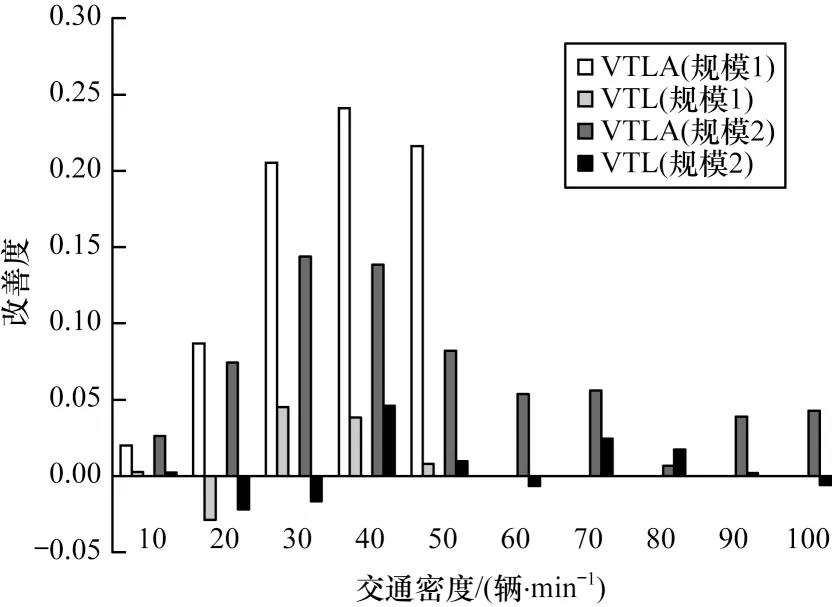
图7 评价值高的车辆相对于所有车辆平均行驶时间的改善度Fig.7 Improvement of vehicles with high evaluation value relative to average driving time of all vehicles

由于近似堵车，图7 不再展现规模1 中十字路口的交通密度在60 辆/min 以上的改善度。高评价值的车辆已无优势。图7 说明VTLA 中出价高的车辆能较快地离开路口区域，交通密度为30 辆/min～50 辆/min 时改善度较好，最高可接近25%；VTL 中平均行驶时间与出价高低无关。

实验6比较在少量车辆具有高评价值ui的场景下，VTL 和VTLA 在不同的交通密度下高评价值ui车辆的平均行驶时间改善度。参数设置：α=0.5；β=0.9；bi=ui。该场景适用于某些具有强烈通行意愿的车辆，由于特殊原因希望快速通过路口，设ui=1 000。

图8 显示在规模2 的十字路口中，VTLA 相对于VTL 在平均行驶时间上有较好的改善；在规模1 的十字路口中，交通密度为60 辆/min～100 辆/min 时VTLA 和VTL 的平均行驶时间差别不大，这与图5中表现的性能一致。与图6 类似，图9 仅显示规模1中交通密度为10 辆/min～60 辆/min 的改善度。由图9 及式（6）可知，对于少量的具有高评价值的车辆，在平均行驶时间上的改善度较好，对于车辆密度在40 辆/min～70 辆/min 时，改善度能超过20%。但车辆密度为100 辆/min 时，由于本身已处于近似堵车状态，因此具有高评价值ui的车辆由于前面车子无法通行而在通行上没有优势。

图8 具有少量高评价值车辆时所有车辆的平均行驶时间Fig.8 Average duration time of all the vehicles when there are few high valuation vehicles

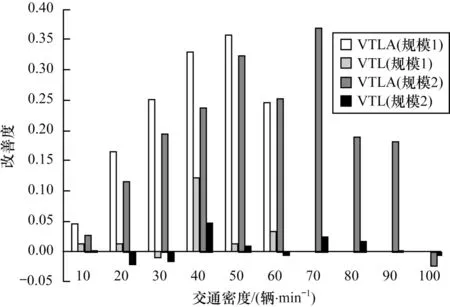
图9 具有少量高评价车辆时高评价值车辆的平均行驶时间改善度Fig.9 Improvement ratio of high valuation vehicles when there are few high valuation vehicles.

3.3 分析与讨论

模拟实验表明本文提出的虚拟交通灯具有策略防护和组策略防护的特性，适用于非可测量因素控制路权的场景。车辆只有在真实展示其私有信息时获得的效用最大，且能够避免车辆形成虚报私有信息的联盟来获取更大的利益。此外，组策略防护的虚拟交通灯比设定绿灯通行数量阈值的虚拟交通灯，在平均行驶时间上有良好的改善，同时高评价值的车辆具有较好的平均行驶时间的改善。组策略防护的虚拟交通灯涉及货币支付，其意义在于每个车辆节点是理性的且明白该过程，他们将不会虚报，这也是纳什均衡中一致性预测的体现。目前虚拟交通灯的实现是内置在车载系统或手机中的一个应用，不管是实际货币支付还是虚拟货币支付均可利用和接入现有的车载或手机中的支付功能。

关于评价值ui的设定，文献［3］中设定车辆的偏好值均匀分布在［0，1，2，3，4］中，无货币单位；文献［13］设定驾驶员的预算均匀分布在［0，500］之间，货币单位为分（cent）；文献［12］设定驾驶员的出价遵循均值为100，方差为25 的正态分布，货币单位为分（cent）；文献［3］设定驾驶员对等待时间缩减的估价遵循均值为1/λ=0.01 的指数分布，无货币单位。可见评价值的设定并无统一模式，只是一种在基于货币激励的方式下产生的驾驶员偏好的货币表现。在同一支付系统中只要保证评价值和支付值具有可比性，产生激励效果即可。

4 结束语

为适用于非可测量因素影响路权的场景，提出一种具有组策略防护特性的虚拟交通灯。通过令车辆合作通过路口，并建模为合作博弈，让虚拟交通灯中的领导车辆发起拍卖，以保证车辆/司机的出价是真实的评价值。利用拍卖的结果建立绿灯信号，使用1 个信号合并算法整合多次拍卖产生的绿灯信号，从而产生合理的路权分配。实验结果表明，组策略防护的虚拟交通灯在保证车辆提供真实私有信息、无合谋行为的基础上，既改善了整体的平均行驶时间又保证了高评价值的车辆能较快通过路口。在实际应用中，城市道路多为三车道，存在十字形、T型和多路交叉口，且实体交通灯与无交通灯的路口通常并存。下一步将研究具有组策略防护特性的虚拟交通灯在多路口多车道中的应用，通过优化实体交通灯和虚拟交通灯在路口的配置比例，提升虚拟交通灯的应用效果。