基于前测的小学数学概念精准教学

董秀娟

[摘 要]文章以“百分数的认识”教学为例，提出基于前测的数学概念精准教学的基本策略，来提升数学概念教学的针对性，使数学课堂教学更加高效。

[关键词]前测;概念;精准教学;小学数学

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2022）05-0051-03

前测是一种前置性的测试。相对于一般的检测，前测不是面向学生的知识，而是面向学生的认知基础和经验基础。之所以在小学数学教学中强调前测的作用，是因为小学数学教学的重要任务之一是进行数学概念的教学。数学概念的教学不仅涉及学生的知识基础，而且涉及学生的能力基础。数学概念教学能够帮助学生夯實知识基础，且能使其形成有效的数学学习能力。无论是哪个教育心理学流派都非常重视学生在学习新知识之前所储存的知识，这些知识通常用前概念、先前经验来表述。因此从教育教学理论的角度来看，借助前测来促进小学数学概念的精准教学，在逻辑上是合理的，在实践中是有生命力的。本文以“百分数的认识”教学为例，论述了基于前测的数学概念精准教学的基本策略，力图为广大教育同仁提供一定的借鉴和思考。

一、基于前测，精准把握学情

基于前测的课堂教学首先要明确“测什么”和“怎么测”的问题。针对“测什么”的问题，教师可从以下两个方面入手：一是前测应该基于学生的认知起点，始终围绕考查学生已有的认知水平和学习经验展开;二是前测内容不宜太多，教师要密切结合教材知识和教学目标来精心设计，在不增加学生负担的前提下把握学生的认知起点。针对“怎么测”的问题，教师可采用练习法、调查问卷法和谈话法进行前测。其中，练习前测法针对性强、操作性强、精确度高，是教师精准把握学情的重要手段。调查问卷法和谈话法侧重于宏观角度，有利于教师从整体上了解学情，但是覆盖面较窄，也难以得到更加精准的量化数据。

前测内容设计如下。

（1）请写出并读出3个百分数。

（2）12.5%和120%是百分数吗？

（3）请举出生活中有关百分数的例子。

（4）[15100]米相当于[30100]米的[50100]。这句话中，哪些分数可以改成百分数？哪些分数不能改成百分数？

对于第1题，超过70%的学生都写出了比较常见的百分数，比如12%、34%、89%等。但是有的学生在写百分号时，两个圆圈写得太大，易与0混淆，这一点教师应帮助学生纠正。另外，在读百分数时，一些学生也出现了类似“把12%读作一百分之十二”的问题。

对于第2题，学生出现的错误较多，超过20%的学生认为12.5%不是百分数，这是受到学习分数时分子不能是小数带来的负面影响。另外，还有超过15%的学生认为120%不是百分数，这说明学生对百分数是否能大于1存在疑感。

对于第3题，学生举出的例子很多，比如我们班有30%的学生会游泳，我们班有15%的学生戴眼镜，等等。这说明学生对生活中的百分数是有一定认识的。

对于第4题，超过30%的学生认为百分数和分数完全一样，在任何情况下都可以互相转化。这说明学生对分数和百分数的不同点还存在认识误区，这一点需要教师在教学中进一步强化。

事实证明，通过这样的前测，尤其是在前测后对测试结果进行分析与统计，能够对学生已有的与“百分数的认识”相关的认知经验进行把握，为后续概念的教学打下坚实的基础。值得一提的是，前测对学生有潜移默化的影响，它会将学生的注意力引到所要学习的知识上。在学生的前概念当中，有很多复杂的知识或者生活经验，只有将其中与所要学习的内容相关的部分挑选出来，原有的经验与所学知识之间的联系才能建立起来。通过这样的前测，学生的注意力会集中到与之相关的经验上来，这实际上就是一个前概念提取的过程，可以为学生夯实数学概念学习的基础。因此从这个角度来看，前测是课堂教学的真正起始点。教学中，教师从“百分数”的核心知识出发，紧紧把握知识的重难点并充分结合学情，以练习题的形式进行了精简的前测，并通过对前测数据的分析了解学生对百分数的认识，从而为进一步优化教学、实现精准教学打下基础。

二、基于前测，初步建构概念

数学教育家弗赖登塔尔认为，数学学习中，与生活联系得越紧密的知识，学生越是记得牢、学得快。在日常教学中，教师可从现实生活入手导入新课，进而吸引学生的注意力，激发学生的探究欲望，拨动学生的思维之“弦”。

【教学片段1】

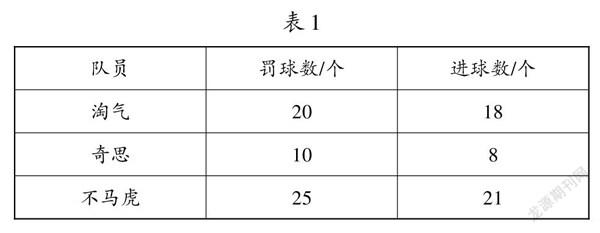
师：在一场足球比赛中，雄鹰队获得了一次罚点球的机会，他们打算从淘气、奇思和不马虎三名队员中选出一名罚点球。下表是这三名队员近期罚点球的情况统计表（如表1）。你觉得应该派谁去？

生1：应该派不马虎去，因为他的进球数量最多。

生2：不对，虽然不马虎进球数最多，但他罚球数也是最多的，我们应该比较三名队员丢球的数量。

生3：淘气丢球的个数是20-18=2个，奇思丢球的个数是10-8=2个，不马虎丢球的个数是25-21=4个，淘气和奇思丢球数量一样，还是不能比较出来谁踢得更准。

生4：我们应该比较进球数占罚球数的几分之几，这样才最公平。淘气进球数占罚球数的[18/20]，奇思进球数占罚球数的[8/10]，不马虎进球数占罚球数的[21/25]。

生5：分母不一样，不好比较。

生4：可以都化成分母是100的分数，分别是[90/100]、[80/100]和[84/100]，淘气的进球率最高，应该派他去。

师：[90/100]可以写作90%，读作百分之九十;[80/100]可以写作80%，读作百分之八十;[84/100]可以写作84%，读作百分之八十四。像90%、80%、84%这样的数叫作百分数，它表示一个数是另一个数的百分之几。

师：同学们在写百分号的时候，要把两个圆圈写得小一些，防止它与零混淆;在读百分数的时候，百分号读作“百分之”，要先读百分号，再读百分号前面的数。

教学中，教师创设了“罚点球”的情境，这个情境既有学生熟悉的生活元素，又起到了一定的测试作用。这样一个既有学生熟悉的生活元素参与，又通过问题来撬动学生思维的前测过程，激发了学生的学习兴趣，同时也吸引了学生的注意力。学生纷纷对于派谁罚点球的问题发表自己的看法，在你一言我一语的对话中，学生的思维被调动起来。教师结合学生讨论，顺势引出“百分数”概念，并就百分数读写问题进行了讲解，解决了前测中暴露出的百分数读写问题，为学生下一步深刻认知百分数打下了基础。

三、基于前测，深化概念理解

数学概念具有较强的逻辑性和抽象性，这对以形象思维为主的小学生而言是个不小的挑战，因此，基于前测的概念建构，教师可从以下两个方面把握。一是要充分运用前测结果。前测是引导教师教学的“风向标”，对于前测中学生认识较为充分的知识点可略讲，对于学生在前测中呈现的认知困惑要采取多种策略进行精讲。二是要注意采取直观化的教学方式。教师可采用展示实物、画图、动手操作等直观手段为学生理解抽象概念铺路搭桥，从而加深学生对数学概念的理解。

【教学片段2】

师：在上面的例题中，如果淘气的罚球数是14，进球数是11，那么进球数占罚球数的百分之几？如何列式？

生1：百分之七十八点五七，列式为11÷14≈0.7857=78.57%。

生2：百分数的分子可以是小数吗？

生3：分数的分子不能是小數，百分数的分子应该也不能是小数。

师：百分数表示一个数是另一个数的百分比，它的分子可以是整数，也可以是小数。

生3：那为什么分数的分子不能是小数呢？

师：我们可以从分数的意义来理解。分数指的是把单位“1”平均分成若干份，表示这样的一份或若干份的数就是分数。那么，你能够取出78.57份吗？

生3：不能。我明白分数的分子不能是小数的原因了。

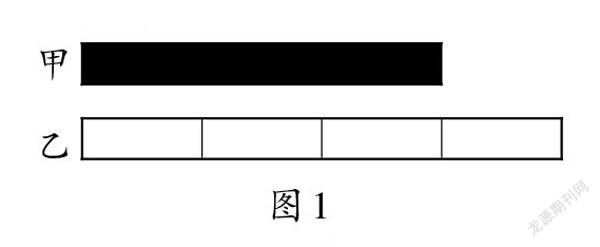
师：请同学们看图（如图1），用百分数填空。甲数是乙数的（ ）？

生1：甲数是乙数的[3/4]，转化成百分数就是75%。

师：那这幅图（如图2）呢？

生2：甲数和乙数一样多，甲数是乙数的100%。

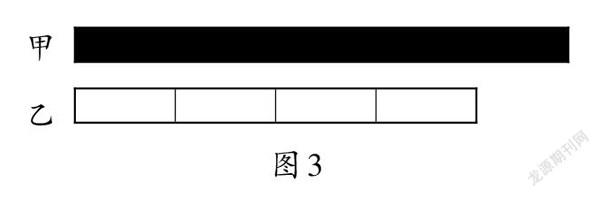
师：这幅图（如图3）呢？

生3：甲数是乙数的[5/4]，转化成百分数是125%。

生4：百分数可以大于1吗？

师：可以的。百分数表示一个数是另一个数的百分之几，如果是一个数比另一个数大的情况，百分数就会大于1。

【教学片段3】

师：“剪去一段绳子的[50/100]”和“剪去一段绳子的[50/100]米”这两句话中的哪一个[50/100]能够改写成50%？

生1：[50/100]=50%，在哪种情况下都能互相转化。

生2：不对。第一个[50/100]表示两个数字的倍比关系，可以改写成50%;而第二个[50/100]米表示的是0.5米，它不能改写成50%。

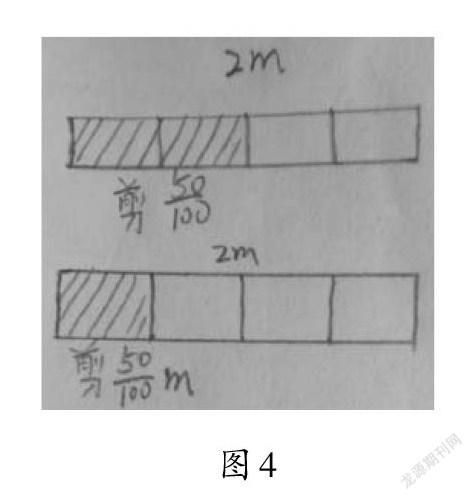
生3：可以通过画图（如图4）来解决这个问题。在第一个图中，绳子长2米，剪去[50/100]就是剪去一半，也就是剪去1米;而在第二个图中，绳子依然是2米，剪去[50/100]米，就是剪去0.5米。因此，这两句话表达的意思是不一样的。第一句话中的[50/100]可以改写成50%，而第二句话中的[50/100]不能改写成50%。

师：对。百分数表示的是一个数是另一个数的百分比，也就是说它表示两个数的倍比关系，不能表示具体的量，因此它不能带单位;而分数既可以表示两个数的倍比关系，又可以表示具体的量，当它表示具体的量时需要带上单位。

纵观整个教学过程，始终是围绕着前测中学生的认知困惑而展开的。在教学片段2中，教师通过对比百分数和分数的意义，阐释了百分数的分子可以是小数的原理，纠正了前测中学生对于百分数分子只能是整数的认识误区。同时，教师通过引导学生画图，使学生真切体会到了百分数的分子可以大于100，并由此拓展了百分数的外延。在教学片段3中，教师通过举实例、画图的方法使学生深刻理解了分数在哪些情况下可以改写成百分数，在哪些情况下不能改写成百分数，从而沟通了百分数与分数之间的内在联系，深化了学生对百分数的本质认识，解决了学生在前测中对分数与百分数关系认识不清的问题。

总之，前测是提高数学概念教学、促进教学精准化的重要手段。教师要结合教学内容，基于数学概念的本质，精心设计前测内容，努力找到学生现有认知与新知学习之间的衔接点，实现前测与课堂教学的“无缝对接”。这个过程中，教师要注意前测内容与方式的设计，将生活与数学有效衔接起来，用灵活的形式来吸引学生的注意力。事实证明，只有同时面向学生的生活与数学的前测，才能在学生的认知基础与所要学习的数学内容之间搭建一座坚实的桥梁。有了这样的准备之后，教师还要采取多种教学策略，逐个突破学生在前测中的知识难点，最终提升数学概念教学的针对性，使数学课堂教学更加高效、精准。

[ 参 考 文 献 ]

[1] 吴敏.小学数学学情前测的策略例谈[J].湖南教育（D版），2020（5）：30-31.

[2] 薛小梅. 数学前测单在小学数学教学目标达成中的作用[J].新课程（小学），2019（1）：18.

[3] 彭柳萍. 柳暗花明又一村：例谈前测在小学数学教学中的作用[J].小学教学参考，2014（17）：8-9.

（责编 黄春香）