基于学习分析的小学数学学习干预模型构建研究

杨文理 钟绍春 赵雪梅 范佳荣 杨澜 钟卓

摘要：智能技术的应用，对于大多数学生而言，的确起到很好的支撑与促进作用。但是，在小学数学教学中，仍有一些学生在一些内容上存在这样或那样的学习困难，亟待研究与探索智能技术条件下有效解决学困生学习困难的干预模型。该文对国内外学习干预模型的相关研究做了系统分析，剖析了小学数学学困生学习困难的主要成因。从学习目标与活动、学困表现、干预策略、支撑环境四个方面及其相互作用关系的角度提出了学习干预模型的构建思路。提出了由学习结果和过程数据采集、学业水平和学习特征分析、学习诊断与干预和学习干预效果评估等构成的学习干预模型。针对疑难知识难以理解问题提出了合理降低学习梯度并搭建适合认知支架和通过在生活情景完成学习活动进而降低认知负荷的干预策略；针对学习兴趣不足问题提出了通过生活化问题/任务激发学习欲望、通过知识趣味化调动学习积极性、通过正向激励提升自我效能感的干预策略；针对专注力不足问题提出了通过分层递进问题/任务增加学习粘性、通过全过程多感协同交互增加学习投入、通过优长潜能释放提升学习参与持续度的干预策略。

关键词：智能技术；学习分析；干预模型；干预策略；数学学困

中图分类号：G434 文献标识码：A

* 本文系教育部-中国移动科研基金项目“构建‘互联网+条件下的新型课堂教学模式创新实证研究——以宁夏石嘴山市实验中学为案例”（项目编号：MCM20180604）研究成果。

一、引言

由于小学生自控力不足，数学学习内容相对抽象、难度较大，致使部分学生在课堂学习中会出现学习困难现象，教师如何减少或避免课堂教学中学生学习困难现象的出现是亟需解决的问题。智能技术的快速发展和普及应用，虽然已经为小学数学疑难知识理解、复杂问题探究提供了有效的支撑，促进了课堂教学的变革和创新，极大的提升了学习质量和效率。但是，在小学数学教学中，仍有一部分学生在一些内容上存在这样或那样的学习困难，特别是，个别学生（学困生）在大多数小学数学学习内容上存在学习障碍与困难。导致学困生学习困难的深层次原因是多种多样的，但是主要的原因是注意力不集中、兴趣不足、学习方法不得当等。正是这些原因，致使学困生难以顺利提取数学事实、建立数学知识体系、形成数学问题解决能力。这些问题严重制约着数学学困生数学思维的培养以及数学能力的塑造。小学阶段是数学思维养成的关键时期，所以帮助数学学困生解决数学学习困难问题，不仅关系着学生学业发展，更关系着学生未来的生存发展。小学数学学困生学习问题有效解决的途径与策略，特别是学习有效干预模型的研究已成为研究热点。

二、研究现状

（一）数学学习困难成因诊断

数学学习困难（简称数学学困）也可称为数学学习障碍，是指学习者智力正常且无其他器质性神经损伤，仅由于个人数学能力不足而导致的在数学成绩上明显落后于同龄学伴的现象[1]。导致数学学习困难的原因是多种多样的。当前，国外研究学者对造成数学学习困难的成因有四种理论。第一种理论认为学习困难主要是由于学习者利用视觉、听觉等通道对信息或知识进行加工时产生冲突而影响学习效果。第二种理论主要集中在学习者的注意力，也称为注意力缺乏理论，该理论认为学习成绩不佳主要是由于注意力结构不稳定引起的，注意力水平不足导致学习者无法全神贯注地学习。第三种理论侧重于学习者的非智力因素，一些研究者认为学习动机不足，学习兴趣低落是导致学习困难的原因。第四种理论认为造成数学学习困难的原因是由于学习者获得信息、使用信息的过程不合理，使用错误的方式方法对信息进行加工、重构[2]。随着对数学学困生特质的深入研究，研究学者进一步对研究群体细化分类，从宏观笼统的关注数学学困生进化为详细、专注地研究单一型数学困难表征。从困难复杂性来看，数学学习困难可区分为单一型数学学习困难以及混合型数学学习困难，也就是我们常说的数学学习困难与阅读困难共有并存[3]；从可能引起数学学习困难的内容上看，可分为数学基本知识学习困难和问题解决困难[4]。国外研究人员针对数学学习困难在认知缺陷、数学概念、计数、算术策略等方面也取得了非常大的实质性进展[5]。

综上所述，小学阶段数学学习困难的成因主要有以下几个方面：（1）数学学习动机不足、学习情绪低落；（2）学习专注力不够；（3）在知识获取过程中，听觉和视觉的调动及协同不足；（4）学习过程中所采用的学习方法不适合，有效性不高；（5）知识体系不完整。

（二）学习分析

学习分析技术是分析学习效果，优化教育教学活动的有效技术，得到了国内外学者的普遍关注和重视。学习分析技术最早由乔治·西蒙斯（George Siemens）提出，他认为学习分析技术是深度挖掘学习者在学习过程中产生的海量学习数据，并且利用分析模型以期发现信息和社会之间的关联，并做到对学习预测以及为学习提供有效建议[6]。李青等认为学习分析是预测并诊断学生在学习过程中存在的问题，并能通过数据的分析研究而改善学习效果的一类技术[7]。何克抗先生认为学习分析技术是利用数据统计处理工具，从教育教学过程中产生的大量学习数据中，通过整理分类、统计、分析等方式，提取出隐藏的、潜在的、有应用价值且涉及到教与学或者教学管理过程的信息和知识与模式，从而达到为教育教学提供智慧指导的技术[8]。

综上所述，学习分析技术是将所有与教学过程息息相关的信息和数据进行汇总，运用不同的技术、方法，对数据进行处理、分析，重新诠释定义这些数据。学习分析技术能够帮助教师根据每一个学习者的个性需求更好地提供定制化的教学服务。教师可以通过解读分析数据，优化教学过程、梳理教学规律并对教学效果进行评估，从而为学习者提供及时的反馈，帮助学习者改进学习方式方法，提升学习质量。同时，通过对分析模型的构建，以及分析和解释数据的过程，可以更好地辅助教学工作者和教育管理者更高效地工作。

目前对学习分析的探索主要聚焦于理论研究与应用分析，普遍认可且广泛采用的学习分析技术模型主要有学习分析概念模型和目标导向的学習分析模型。赵蔚等人以学习者为研究个体，以相关学习数据为研究主阵地，构建了在线学习分析模型，并且对此进行了大量的实证研究[9]。马杰利用分层建模思想，在分析对比国内外学习分析模型构建的研究基础上，构建了能够对学习成绩进行预测的模型[10]。武法提等人通过对国内外学习分析模型的梳理分析总结存在问题，并基于个性化学习模式和相关文献构建了数字化学习环境下个性化行为分析模型[11]。

（三）学习干预

学习干预指在一定科学理论基础上，针对特定学习对象，在一定学习环境下，针对学习困难方面，有目的、有计划地采取直接或间接策略或行为，以帮助学习者攻破学习困难的现状，提升学习能力。其中使用最为广泛的是“干预—反应”（Response to Intervention，简称RTI）。RTI干预层次分为三级，多级干预确保每位学习者都能获得科学合理的学习支持，并且每个层次嵌套多种干预方式[12]。这是一种提倡准确分析、科学评估学情，精准干预学习困难学生的教育方法，在课堂教学过程中教师根据学生学情特点实施干预，通过实施干预解决学习困难问题，同时对学习困难解决程度进行评估，在评估基础上，为学困生提供更精准、科学的个性化学习指导，提升学习效果。

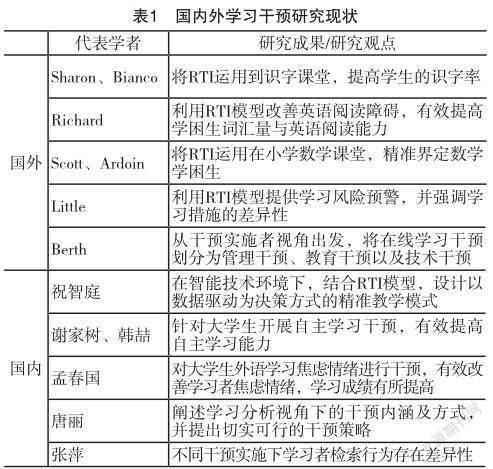
RIT模型的第一个层次为一级干预，这一层级的干预对象是面对全体学习者，干预目的是对学困现象起早期预防作用，是最普遍、针对性最低的监控和干预方式，一级干预大概会对班级80%的学习者起有效作用。二级干预，主要针对部分学习者，增强监控力度，加大干预措施，这一层级针对的是，在完成一级干预后，依旧没有达到学习标准的学习者，并对他们实施更为深入学习干预措施。RTI模型的三级干预，是针对个别学习者，采用的是密切监控、以及个别深入干预的方式。RTI模型自提出以来得到广泛的应用。国内外研究学者将RTI模型运用在不同学科、不同教学情境中、设计了以RTI模型为基础的精准教学模式，实验研究均取得了显著成效，如表1所示。

近年来国内外针对学习干预的发展已趋于成熟，研究学者从不同角度，根据干预需求，构建了干预模型，并进行了大量实证研究。但研究大多局限于传统课堂教学环境，利用传统教学手段和方式实施干预，缺乏精准动态学习数据，所实施的干预缺乏及时性、精准性。干预策略更多借助常规手段，人为干预为主，干预效果存在局限性，在智能技术手段支撑下的干预策略研究还比较匮乏。本文针对当前研究所存在的问题，着重开展基于学习分析技术的学习干预模型构建和智能条件支撑下的干预策略研究。

三、小学数学学习干预模型构建

（一）学习干预模型构建思路

由班杜拉提出的三元交互理论认为个体行为是受社会环境影响制约的，个体的大多数行为活动可以通过对周遭环境的观察和模仿获得[13]。个体的行为与周围环境、个体因素是彼此影响、相互作用的，而且缺一不可。个体行为不仅受遗传因素制约，还受心理特征（特别是个人认知）以及环境所影响。学习个体通过观察和学习，接收环境中的各种信息，对自己的认知结构进行调整，在此基础上改善和调节学习行为。该理论主要是对个体的行为、环境进行总体分析和阐述，更多的是基于宏观抽象层面的。基于该理论的研究与实践，主要是在常规条件下开展的，对智能技术条件下的相关研究还不成熟。在智能技术条件下，基于学习分析技术如何构建学习干预模型，按照什么样学习干预策略实施学习干预等，已经成为学习干预研究的重要问题。

本文以三元交互学习理论为依据，针对学困生普遍存在的问题，通过对学生以及学习行为、学习环境三种因素之间的关系进行改进和扩充，提出了在智能技术支撑下，基于学习分析技术，从学习目标与学习活动、学困生学困表现、学习干预策略、学习支撑环境等四个方面及其相互作用关系的角度构建学习干预模型的思路，如图1所示。

学习目标与活动、学困表现、干预策略、支撑环境是学困生学习干预模型的四个相互作用的重要组成部分。小学数学学习目标主要包括知识技能、数学思考、问题解决以及情感态度等方面，对于大多数学生而言，在一般知识的学习上基本上没有太多的障碍，主要的问题出现在疑难知识的理解、复杂问题的解决及数学思考等方面。而学困生则不然，往往在一般问题学习上就出现了障碍。出现障碍的原因是多方面的，比较突出的原因主要包括学习活动安排不适合，在学习活动过程中难以保持兴趣、学习专注力不足等。因此，在学习干预方面，应该针对这三方面的问题制定相应的有效干预策略。但是，仅有干预适合的干预策略，没有有效的干预支撑手段和条件，也很难将干预策略实施下去。单纯依靠常规手段和条件，很难满足干预对手段与条件的需要。人工智能、大数据、VR/AR等技术能够为干预实施提供全新的手段与条件，因此，充分发挥智能技术手段的优势，提供干预实施所需要的支撑手段与条件，是建立有效干预模型的基础保障。

（二）学习干预模型结构

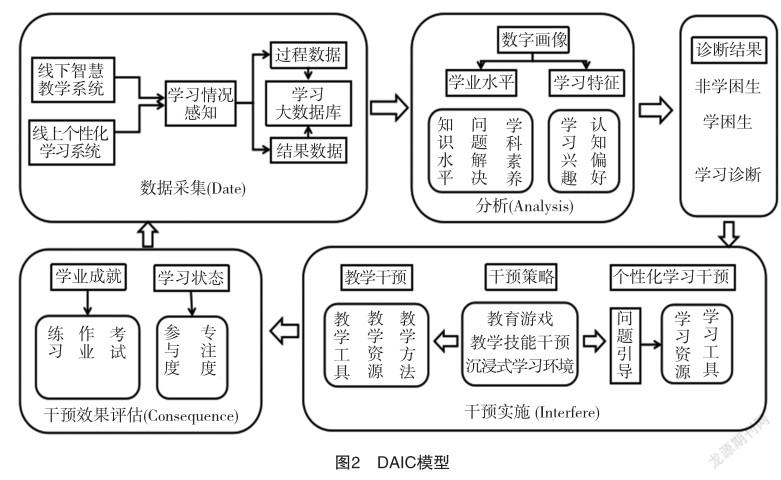
按照上述的学习干预模型构建思路，提出了由学习结果和过程数据采集、学业水平和学习特征分析、学习诊断与干预和学习干预效果评估等构成的学习干预模型（DAIC），如图2所示。

1.學习数据采集

学生相关学习数据主要是通过线上个性化学习系统和线下智慧教学系统两种渠道获取的。因此，要想对小学数学学困生进行精准干预，就必须能够全过程、完整、精准、科学采集来源于线下智慧教学系统和线上个性化学习系统中的课堂教学和学生学习情况大数据。学生的学习数据，主要包括学生学习路径、所使用课程资源及频次、学习时长、作业提交时长、支撑工具使用情况、学习状态特征等过程性数据，以及测试成绩、作业完成情况、自我评价、学伴互评、教师评价等结果性数据。

学习结果数据的获得，主要是通过问题解决和任务完成等方式实现。仅靠零散的问题/任务是很难系统、科学采集到精准反应出学生学习水平的数据。因此，需要有能够系统、科学、全面反映学习水平的量化标准作为依据来采集学生学习数据，即学科课程图谱[14]。而学习过程数据的获得，主要是从学生利用学习系统开展学习活动所留下的学习资源、学习工具、系统支撑功能等的使用痕迹数据中获得。其中，学习路径数据较难获取。如果事先不清楚有几种可能的学习路径，则学习路径数据的获取，就没有明确的方向，也无法建立学习路径完整的大数据库。因此，应事先按照学习内容的特点、学生可能的学习情况，建立可能的学习路径体系，即学习路网[15]。依据学习路网采集学习路径信息，才有可能精准获取学习路径相关的数据。

2.学习分析与诊断

利用依据课程图谱所采集的学习结果数据，能够精准分析出学生知识掌握情况、运用知识解决问题的能力形成情况及学科素养培养情况。利用基于学习路网所采集的过程性数据，则能够精准的分析出什么样的学习路径、学习资源与工具、学习系统与终端设备对学生知识学习更有帮助。基于学生学习结果数据和学习过程数据，构建学生学业水平和学习特征画像。其中，学业水平画像包括知识水平、能力水平和素养水平，学生学习特征画像包括学习兴趣、学习偏好等。在此基础上，根据学生学习画像，分析诊断出学生学习困难点及学习困难出现的原因，形成分析报告，为学困生干预内容和策略的选择提供科学依据。具体的分析与诊断原理如图3所示。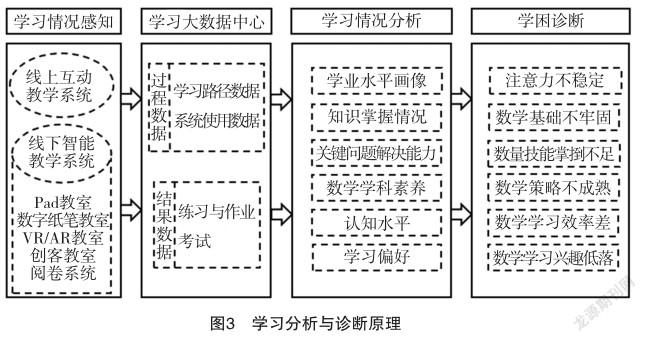

3.学习干预实施

当学习分析与诊断模块中分析诊断出学生存在学习困难时，就需要采取有针对性的干预措施对学困生进行有效的干预，帮助学困生解决学习困难。不同的学习困难，所要采取的干预措施也不尽相同。需要针对学习困难的成因，从干预策略库中选择合适的干预策略和干预方式，对学困生进行有针对性的干预。由于学习困难不是一次干预就能够解决的，大多数情况下需要多次干预才能完成，因此学习干预是一个迭代递进的过程，每次干预强度随着干预的递进逐级上升。在每一级干预实施后，都需对实施干预的学困生进行干预效果分析与评估。如果学习干预实施效果并未达到预期目标，将采取进一步的迭代递进干预。

从哪些方面对学困生进行干预，采取什么样的干预策略，将直接决定干预进程和干预效果。一般情况下，学困生学困表现主要体现在知识掌握程度不足，关键问题解决能力形成不够。导致学困的原因主要是认知结构欠缺、学习兴趣不足，在学习过程中专注度低，致使已有知识基础薄弱，甚至是知识体系不完整。因此，学习干预应针对学困生各自的不同情况及成因，有针对性地选择重点干预内容和适合的干预策略，实施干预活动，才能取得预期的效果。

除此之外，决定干预效果的另一个重要因素是干预工具和手段，在常规条件下，可采取的工具和手段或多或少存在一定的局限性，尽管对学困生的成因诊断可能非常精准，选择的干预策略非常适合，但是，由于缺乏有效的干预手段和条件，往往很难取得预期的效果。因此，借助智能技术手段，根据不同的干预策略，分别提供有效的学习工具、学习资源支持干预活动，是解决这一问题切实可行的途径。

4.干预效果评估

对学困生的学习干预是一个迭代递进的过程，每次干预是否达到预期效果，需要通过精准评价才能确定。干预效果评价分为过程性评价和终结性评价，过程性评价主要以单级干预为单位开展评价活动，根据评价结果决定是否进行下一级干预。教师利用学习大数据，从学困生的学习参与度、学习专注度、知识掌握情况、问题解决能力等方面，综合分析、评价干预实施的效果，根据干预实施的评估效果决定是否实施新一轮的干预。终结性评价是对已实施的多级干预进行综合评价，目的是对所选择干预内容和方式的有效性进行评价。终结性评价，首先是对每一级干预进行综合评价。每一级的综合评价需依据学困生干预起始学习状况数据和干预后学习状况数据，对所选择的干预内容和方式进行综合评价。在每一级干预综合评价基础上，给出所实施多级干预有效性的评价。

在开展干预效果评价工作中，首先需要解决的问题是从哪些方面来衡量干预活动效果的好坏。在综合研究小学数学课程标准和小学数学学困生学情特点的基础上，本文认为干预效果评价应从多个方面开展，具体包括数学知识掌握程度、数学关键问题解决能力水平、数学学科素养形成水平、课堂参与度、学习专注度和学习效率等方面，如图4所示。其中，知识掌握与关键能力解决主要从数、数量、数学符号等元素中建立数学概念，理解数、符号等数学概念，正确选择运算程序与方法等方面进行评估。干预效果的评估分析十分重要，干预实施者在此基础上不断检验、迭代和完善学习干预模型，检验学习干预的效果，最终以达到学困生学习态度的调整、学习行为的改变以及学习质量的提升等效果。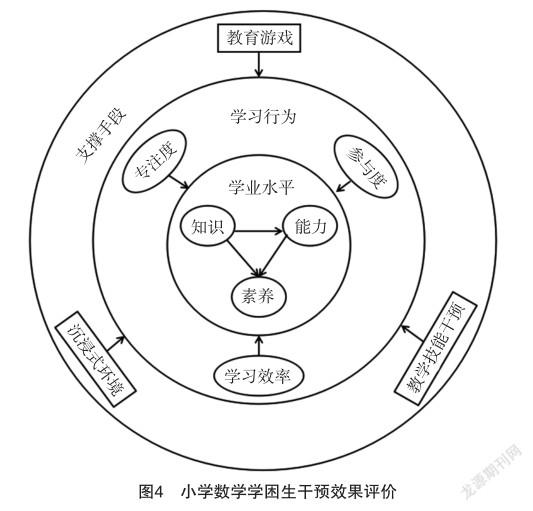

教与学是一个复杂的过程，造成学困的成因是多种多样的，学业水平的提升也非一蹴而就，所以干预模型是一个动态迭代进化模型，通过干预过程的不断迭代进化，进而解决学困生所存在的学习问题。

四、小学数学学困生干预策略

导致小学数学学习困难的原因是多方面的，其中主要原因有注意力不集中、学习兴趣不足、理解力不强、知识记忆弱、学习方法不恰当等。因此，应针对导致学困生学习困难的不同原因，结合这个年龄段孩子的认知规律和思维发展特点，分别研究和制定相应的干预策略。

（一）知識理解难的干预策略

导致学困生在小学数学学习困难的首要原因是理解知识困难，无法完成相应的学习活动。诸如，在课堂教学中经常会出现运算方法混淆、不会退位减或进位加、数感认识有偏差等问题。而教师多是让学生通过大量反复训练等方式，帮助学困生加深对知识的记忆与理解，但这种做法成效并不显著，往往会导致学困生更加厌学，使得学习质量不升反降。出现这一问题的主要原因有两个方面：一是教师所安排学习活动中的学习梯度超出学困生的认知能力和水平，导致学生难以理解知识；二是教师直接以抽象数字及其运算关系来讲解相关知识，学困生难以与生活实际建立联系，从而产生认知障碍。因此，对小学数学学困生的干预应着重从上述两个方面入手，有针对性的制定能解决上述两方面问题的干预策略。

1.降低学习梯度，搭建适合认知支架

在课堂教学活动设计时，教师会根据班级大多数学生的认知能力与水平来统筹安排课堂教学活动。由于学困生的认知水平相较于普通学生而言有一定差距，因此，按照这样的教学活动安排开展学习活动时，往往会出现知识理解不透彻，问题解决能力难以系统形成等情况。要想从根本上解决这一问题，不调整教学活动安排，对于学困生而言是不可能的。教学活动安排调整的关键是，如何将薄弱点的学习活动梯度降低到学困生能够接受的层面。除此之外，还应为学生按照该学习梯度提供适合的认知支架，实施进阶式干预，使其能够顺利高效的完成疑难知识的学习。

例如，在学习除法时，教师通过帮小鸟建房子问题，驱动学生学习，“一间房子能装6只鸟，42只鸟需要建多少间房子？”在一般情况下，老师会用表2来引导学生思考并解决这一问题。老师只会给出序号为1—7共7个房间号，鸟数量是空的，驱动孩子思考并填写房间号下面累计的可容纳鸟的总数。

从课堂教学实际情况看，对于大多数学生而言，完成这一任务没有什么障碍。多数学生会根据房间号，得出累计鸟数量，即房间号每增加1，可容纳鸟的数量会增加6个。但是，对于学困生而言，会出现填写不正确的情况。比如，有的学困生在每个房间号下面都填寫“6”，有的学生就是全部填不上。出现这一情况的原因是学习活动安排的梯度超出学困生的认知水平，学习支架不能有效支持学生学习活动完成。要解决这一问题，教师应合理调整学习活动安排，降低学习活动安排梯度，使之与学困生的认知能力吻合，并为学生提供适合这一认知梯度的学习支架。针对为小鸟建房子问题，可通过增加让学生回答每个房间可容纳鸟的数量和每个房间鸟编号这两个学习活动，来降低学习活动梯度，如表3所示。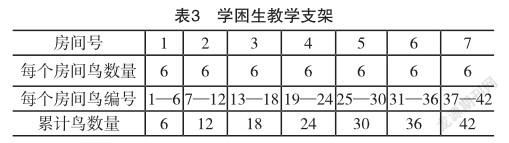

教师首先出示仅有7个房间号的空表，然后让学困生回答每个房间可容纳鸟的数量。对于这一问题，学困生可根据题干信息很容易得出每间可装鸟的数量为6。接下来，教师让学生根据对所有鸟进行编号，并给出每个房间所装鸟的编号区间。在此基础上，让学生计算出该房间及之前所有房间累计所能容纳的鸟的数量。通过给出每个房间可容纳鸟的数量及鸟的顺序编号区间，降低学生问题解决梯度，从而顺利解决问题。这样的学习活动过程，虽然在纸上可以完成，但是不够便利和方便，借助数学学习工具，能够为学习学习提供有力的支持和帮助。

2.通过生活情境完成学习活动，降低认知负荷

为了提高教学效率，教师一般会以抽象数字及其运算关系来讲解相关数学知识。从知识理解角度来看，大多数学生采用这种教学方式学习知识，不会出现太大的认知障碍。但是对学困生而言，可能就会出现认知上的困难。这种情况下，不改变知识学习方式难以解决学困生的学习障碍问题。学困生出现认知困难的原因，主要是难以通过抽象数字来学习数量之间的运算关系，因此，解决学困生这方面的认知困难，应从将数量间运算关系与学生可接受的生活化问题建立联系，基于此来降低学生的认知负荷，让学生能够找到完成这类知识学习的切实可行途径。

例如，在学习除法时，教师通过“有21个桃子，要平均分给7个小猴子，每个小猴子能分到几个桃子，每个猴子所得到的桃子占所有桃子的份额是多少？”对于这一问题，大多数学生能够直接列出“21÷7”这一算式，运用抽象数字和其运算关系来得出每个小猴子能得到几个桃子的结论。但是，对于学困生而言，则可能会出现要么不会列算式，要么列成“7÷21”错误算式的问题。究其根本原因，是学困生没有真正理解除法的基本含义。在这种情况下，即便是再给更多的测试问题让学生求解，也不见得能解决这一问题。要想解决这一问题，教师最好是通过建立真实的生活场景，将数量关系情境化，帮助学生理解除法的本质含义，即平均分是谁来分被分的东西。在常规条件下，教师通过黑板粉笔来建立真实的生活场景是有难度的。借助信息技术手段，教师可以将7只小猴子和21个桃子的关系可视化呈现给学生，如图5所示。通过这样的可视化手段，形象直观地阐述清楚将21个桃子平均分给7只小猴子，其本质是将21个桃子分成7份，每个猴子1份。每一份桃子的数量是3个，每个猴子得到所有桃子的1/7，这是两个不同性质的数字。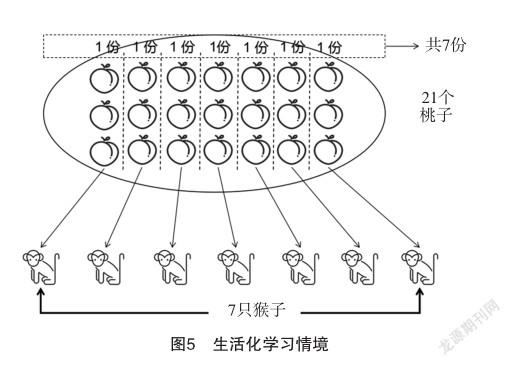

（二）针对学习兴趣不足问题的干预策略

导致学困生兴趣不足的原因是多方面的，其中比较主要的原因有所学知识与生活实际缺乏联系、知识学习缺乏趣味性、知识学习缺乏自我效能感等。针对这一实际情况，分别提出了通过生活化问题/任务激发学习欲望、通过知识趣味化调动学习积极性、通过正向激励提升自我效能感的干预策略。

1.通过生活化问题/任务激发学习欲望

针对所学知识与生活实际缺乏联系导致的兴趣不足问题，最好的解决办法是通过将抽象的知识转化为生活化问题。通过情景化的问题，一方面帮助学生全面搞清楚所学知识的用途与价值，最大限度激发学生解决问题的欲望，使得学生有兴趣学习该知识；另一方面，能够驱动学生完成知识的学习，使得学生在学习过程中能够保持对学习该知识的渴求与欲望。

例如，在学习长度计量单位时，长度的计量单位有千米、米、分米、厘米、微米等。一般情况下，教师通过直接让学生学习千米、米、分米、厘米、微米，以及它们之间换算关系。按照这种学习方式，大多数学生能够接受这些知识，并运用这些知识完成一些计算问题。但对于学困生而言，往往会出现不感兴趣、不愿意学的情况。针对这一问题，比较切实可行的解决办法是教师通过生活化的场景，让学生知道为什么有这些知识、为什么要学这些知识，让学生真正对这类知识学习感兴趣。比如，高铁的时速用每小时行驶多少千米来表达是比较符合实际情况，但如果用每小时行驶多少厘米来表达的话，从理论上讲没有错误，从实际应用角度来讲，就难以简练清晰的表达出来。再比如说人的身高，如果用千米表达的话，人的身高就在0.0001—0.003千米之间，这样的数据同样使用起来很困难。用米为基本单位，精确到厘米这一精度，是比较方便的。

2.通过知识趣味化调动学习积极性

好奇心是孩子的天性，处于小学阶段的学生，极易容易对有趣的东西充满好奇心。对于较难的数学知识，如果仅通过抽象的数字、数字之间的对应关系等来完成这些知识的学习，学困生往往会出现学习困难，极易丧失学习的兴趣与积极性。将知识趣味化，是解决这一问题比较有效的途径与办法。

例如，有2、6、8、9四个数，让学生分析任取两个数之和是偶数或奇数的可能性哪个更大，或者是有两组2、6、8、9四个数，每次从一组中抽取一个数，两数之和是偶数或奇数的可能性哪个更大。对于这样的问题，大多数学生可以直接计算并得出结果。但是，学困生可能会出现不感兴趣、不愿意参与等问题。通过将问题转化成甲乙两个人玩扑克牌游戏，一种情况是两个人手里分别拿着2、6、8、9四张扑克牌，每次从各自的扑克牌中抽取一张，若两张扑克牌之和为偶数则甲赢，若为奇数则乙赢。另一种情况是，只有2、6、8、9这四张扑克牌，从这四张扑克牌中，甲乙两人分别抽取一张，若抽取的两个扑克牌之和为偶数则甲赢，若为奇数则乙赢。这两种情况对甲乙二人是否公平，为什么？通过这样的趣味化问题，可以有效激发学生學习积极性。

3.通过正向激励提升自我效能感

与大多数学生相比较，一般情况下，学困生的自我效能感较低，对独立解决问题/完成任务缺乏足够的信心，致使学习的积极性与主动性不足。针对这一情况，想要真正提升学生的积极性与主动性，比较有效的途径是尽可能增强学困生的学习自我效能感。因此，在教学过程中，教师应通过鼓励、表扬、奖赏等激励方式，尽可能对学困生的学习活动给予正面的积极鼓励。当学困生出现问题的时候，应引导学困生发现问题、分析问题出现的原因，找到解决问题的办法，使学困生充分感受到自己能够有足够的学习能力完成学习活动，从而提升自我效能感。例如，教师利用网络学习空间动态、全面展示学困生参与探究学习、项目学习、合作学习等各种学习活动，所取得的学习成果，并给予多类别、多层次的表扬，帮助学困生提升自我效能感。

（三）针对专注力不足问题的干预策略

学困生专注力不足问题出现的原因是多方面的，其中比较主要的原因有学习粘性不强、学习投入不足、学习持续度不高等。针对学困生专注力不足的主要原因，分别提出了通过分层递进问题/任务增加学习粘性、通过全过程多感协同交互增加学习投入、通过优长潜能释放提升持续度的干预策略。

1.通过分层递进问题/任务增加学习粘性

对于大多数学生而言，只要设计出能够覆盖知识各种应用边界情况的学习驱动问题和任务，即便不是一体化分层设计的，也能够让学生有足够的专注力完成学习活动。但是，对于学困生而言，如果任务不是分层递进一体化设计的，学困生很难保持连贯的认知，可能出现注意力分散的情况。因此，应以学生的生活和认知经验为基础，针对一个情景不断延展学习内容，由易到难、层层递进，增加学困生的学习粘性，进而提高学生的专注力。

例如，在学习“有余数的除法”时，教师讲解什么是余数、什么情况下会有余数之后，大多数学生能够完成有余数的除法运算。然而，对于学困生而言，往往会出现不知道从何下手完成运算的情况。这种情况下，仅靠老师进一步讲解或者是重复练习，很难解决这一问题。出现这一情况的主要原因是学困生不会在整除运算基础上，解决有余数除法运算问题。这一问题切实可行的解决办法是，通过学生能够完成的整除问题引出有余数的除法运算问题，为学生提供学习支架，学会有余数除法的运算。还以小鸟修房子为例，在学生已经能够完成整除运算的基础上，进一步给出问题“如果有43只小鸟，需要修几间房子？”。通过前面的学习，学生已经清楚42只小鸟需要修建7间房子，且恰好能够全部装下。此时，多出了1只小鸟，按照此前学习的除法知识，无法解决该问题。这种情况该如何处理？教师应适时引入余数的概念。该问题的生活实际意义是，当多出1只小鸟，就需要多修建1间房子，但并不是再多出1只小鸟，还要增加一间房子，只要房子没住满6只小鸟，就不需要额外再修建房子。通过这样的问题，引导学生理解余数的本质内涵，完成不能整除情况下的除法运算。在层层递进的问题牵引下，增加学困生的学习粘性，使其积极投入到学习当中，完成学习任务。

2.通过全过程多感协同交互增加学习投入

在数学抽象知识学习过程中，大多数学生通过一般教学手段能够完成认知和运用，对于学困生而言，用一般手段学习就专注不进去，最好是能调动多感协同，使学生始终处于活跃的状态。在传统课堂教学中，受常规教学条件的限制，学困生只能通过黑板、书本等媒介获取知识，这种方式的弊端是学困生获取知识的渠道抽象、枯燥，致使学困生的学习投入严重不足。运用VR/AR等智能技术调动视觉、听觉、触觉多感协同，为学困生营造高沉浸、全流程的学习问题解决/任务完成的环境，持续调动学生学习投入度。

例如，在学习物体的相对位置关系这一内容时，对大部分学生而言，通过空间想象能力能够学会这部分内容。但对于学困生而言，空间感不足是较难完成这一内容学习的。利用VR/AR技术，让学习者置身于美丽的园林之中，学习者通过园林中的导航，操控手柄到达园林中不同的位置，判断不同建筑物之间的位置关系，多感协同的学习氛围弥补了学困生空间感、抽象思维不足的问题，最大限度的增加学困生的学习投入，提升其学习专注力。

3.通过优长潜能释放提升学习参与持续度

在班级授课制的课堂教学中，学习相对优异的学习者往往有更多的表现机会，致使学困生的班级展示自己的机会相对较少，使其学习持续性不高。在教学过程中，教师应引导学困生更好的发挥自己相对擅长且有优势的方面，有助于学习者找到自己的价值感，让学生热爱学习，提升其学习持续度。例如，有的学困生热爱打篮球，教师通过让该学困生分析篮球抛出去的曲线是怎样的，在什么位置、什么角度投篮更容易投进篮筐，通过对投篮位置、角度的分析，总结投篮问题中蕴含的数学几何知识。这样的做法，一方面使学困生通过打篮球这一爱好，激励学困生更深入的研究相关的数学知识；另一方面，学困生在该问题的解决过程中，找到自己的价值感与成就感后，会逐步认同自己、燃起学习其他数学内容的热情，促进学困生的学习的持续性。

五、结语

本文针对引起小学数学学困现象出现的疑难知识难以理解、学习兴趣不足、专注力不足等原因，研究了由学习数据采集、学习分析与诊断、学习干预实施、干预效果评估构成的小学数学学困生干预模型，并针对引起小学数学学科现象的不同原因分别给出了相应的学习干预策略。本文所构建的干预模型和干预策略，在一定程度上能够解决小学数学学困问题，但并不能解决所有的学困问题，因此，关于小学数学学困问题的干预模型，还需要进一步深入研究和探索。

参考文献：

[1] Geary D C.Mathematics and Learning Disabilities [J].Journal of Learning Disabilities，2004，37（1）：4-15.

[2] 陈栩，郭斯萍.国外学习困难学生研究综述[J].教育科学研究，2006， （6）：37-39.

[3] Jordan N C，Montani T O.Cognitive arithmetic and problem solving：a comparison of children with specific and general mathematics difficulties [J]. Journal of Learning Disabilities，1997，30（6）：624-634+684.

[4] Okamoto Y，Case R.II.Exploring the microstructure of childrens central conceptual structures in the domain of number [J].Monographs of the Society for Research in Child Development，2010，6（1-2）：27-58.[5] 黎朝钰，肖维婧等.国外数学学习困难干预研究现状与启示[J].现代特殊教育，2021，（15）：72-78.

[6] 郭炯，郑晓俊.基于大数据的学习分析研究综述[J].中国电化教育，2017，（1）：121-130.

[7] 李青，王涛.学习分析技术研究与应用现状述评[J].中国电化教育，2012，（8）：129-133.

[8] 何克抗.“学习分析技术”在我国的新发展[J].电化教育研究，2016，37 （7）：5-13.

[9] 姜强，赵蔚等.基于大数据的个性化自适应在线学习分析模型及实现[J].中国电化教育，2015，38（1）：85-92.

[10] 马杰，赵蔚等.基于学习分析技术的预测模型构建与实证研究[J].现代教育技术，2014，24（11）：30-38.

[11] 武法提，牟智佳.基于学习者个性化行为分析的学习结果预测框架设计研究[J].中国电化教育，2016，37（1）：41-48.

[12] 牟晓宇，昝飞.美国特殊儿童学业困难反应模式——RTI模式[J].外国教育研究，2011，38（4）：54-59.

[13] 谢幼如，盛创新等.网络学习空间提升自我效能感的效果研究[J].中国电化教育，2016，（1）：34-40.

[14] 钟绍春，钟卓等.如何构建智慧课堂[J].电化教育研究，2020，41（10）：15-21+28.

[15] 钟绍春.人工智能支持智慧学习的方向与途径[J].中国电化教育，2019，（7）：8-13.

作者简介：

杨文理：在读博士，研究方向为智慧学习环境。

钟绍春：教授，博士生导师，研究方向为智慧教育、人工智能。

Research on the Construction of Primary School Mathematics Learning Intervention Model Based on Learning Analysis

Yang Wenli1， Zhong Shaochun2， Zhao Xuemei1， Fan Jiarong1， Yang Lan1， Zhong Zhuo1

（1.School of Information Science and Technology， Northeast Normal University， Changchun 130117， Jilin； 2.Ministry of Education Digital Learning Support Technology Engineering Research Center， Changchun 130117， Jilin）

Abstract： The application of intelligent technology does play a very good supporting and promoting role for most students. However， in primary school mathematics teaching， there are still some students with learning difficulties in some content， it is urgent to study and explore the intervention model to effectively solve the learning difficulties of students with learning difficulties under the condition of intelligent technology. This paper makes a systematic analysis of the relevant studies on learning intervention models at home and abroad， and analyzes the main causes of learning difficulties of students with learning difficulties in primary school mathematics. This paper proposes the construction of learning intervention model from four aspects of learning objectives and activities， learning difficulties， intervention strategies， supporting environment and their interaction. A learning intervention model consisting of learning outcome and process data collection， analysis of learning level and learning characteristics， learning diagnosis and intervention， and evaluation of learning intervention effect was proposed. To solve the problem of difficult knowledge understanding， the intervention strategies of reasonably lowering learning gradient and constructing suitable cognitive scaffold and reducing cognitive load by completing learning activities in life scenarios were proposed. To solve the problem of insufficient interest in learning， the intervention strategies of stimulating learning desire through life-oriented questions/tasks， stimulating learning enthusiasm through interesting knowledge， and enhancing self-efficacy through positive motivation were proposed. In order to solve the problem of insufficient attention， the intervention strategies of increasing learning stickiness through hierarchical and progressive questions/tasks， increasing learning engagement through the whole process of multi-sensory collaborative interaction， and improving the duration of learning participation through the release of superior potential were proposed.

Keywords： intelligent technology； learning analysis； intervention model； intervention strategies； mathematics learning difficulties

收稿日期：2022年1月5日

責任编辑：邢西深