运用整体思维解题“五法”
⦿甘肃省张掖市第二中学 纪相林
1 引言
在解数学题时,学生常习惯于“由小到大”的思维模式,就是从较复杂的“大问题”中的“小问题”入手,先解决较简单的小问题,然后再由小到大,积少成多,逐步扩大战果.但是这种常规的方法并非万能钥匙,面对有些特殊问题,我们深感运算量大、过程繁杂,甚至还可能陷入半途而废的困境.这时,不妨换个思路,站在宏观的角度,把待解决的“大问题”看作是一个整体,通过“聚焦”研究问题的形式、结构与特征,有针对性地采用“代入、联想、合设方程”[1]等多种转化的方法与技巧,最终达到化繁为简、解决问题的目的.
下面结合典型例题,探讨运用“整体思维”解决数学问题的方法与技巧.
2 “整体思维”在解题中的运用
2.1 整体代入法
有些问题在求解时,不能(或不需)分别求出各个量的具体值,只需考虑求出这些量所构成的某代数式的整体值,就能达到解题的目的.
例1已知直棱柱的底面是等腰梯形,且梯形对角线和梯形底边的夹角为α,棱柱的侧面积为Q,设此直棱柱有内切圆柱,求该圆柱的侧面积.

图1
解:如图1,梯形ABCD(AB 2DE=AB+CD. 又根据切线性质,得 AD+BC=AB+CD. 所以DE=AD=BC,故梯形的周长为4DE. 设棱柱的高为h,圆柱的底面半径为R,那么 Q=4DE·h. 在Rt△BED中,DE=BE·cotα=2R·cotα. 点评:如果按照常规解法,首先设直棱柱的高为h,圆柱底面半径为R,则S圆柱=2πRh,但是如何求Rh的值呢?这是关键所在.联想到Rt△BED与等腰梯形、直棱柱同高的特点,我们就可以避开直接计算Rh,而是选择将Rh整体代入的方法.这种避繁就简的方法在立体几何中会经常用到. 整体观察就是从宏观的角度来考察问题的结构与特点,从而找到解决问题的突破口. 解:由原不等式变形,得 该不等式对所有实数x恒成立的充要条件是 所以a的取值范围是(0,1). 点评:通过整体观察,发现不等式左边的三个对数式可以转化为同一类形式.因此,先把不等式变形化简后再求解,这样就避免了繁琐的运算过程.这显然比通常利用二次函数的性质求解简单得多. 对有些特征明显的习题,我们可以根据题型的特点,相应地配出与其相匹配的另一个整体,然后再根据相互之间的关系求解. ② 所谓整体联想,就是通过分析问题的整体结构或特点,找出知识点之间的相似性、相关性等,运用有关知识来解决问题. 因为(α-β)+(β-γ)+(γ-α)=0,所以 tan[(α-β)+(β-γ)+(γ-α)]=0. 整理,可得tan(α-β)+tan(β-γ)+tan(γ-α)= tan(α-β)tan(β-γ)tan(γ-α). 展开,整体联想,代换,即得 点评:经过观察和联想,我们发现原题待证式中的分式与正切的差角公式相似,而且整个等式又与三角形中的公式tanA+tanB+tanC=tanA·tanB·tanC[3]相似,所以可以仿其形式,采用整体联想、合理代换的方法轻松完成证明. 对具有某种性质的两条曲线,如果把它们的方程从整体上合设成一种表达式,就可以收到化繁为简的效果. 图2 求证:|AC|=|BD|. (b2-a2k2)x2-2kma2x-(m2+λb2)a2=0. 设直线与曲线的交点坐标分别为(x1,y1) ,(x2,y2). 所以,两交点连线段中点的横坐标为 所以,线段AB和CD的中点重合. 故|AC|=|BD|. 从上述各例的技巧分析中可以看出,运用整体思维法来解决数学问题,具有极大的优越性与实用性.学生如果学会运用整体思维法来思考问题,就能够不断地开阔思路,激发灵感,灵活自如地运用并创新出一些更实用的方法和技巧[4],最终达到提高解题速度与质量的目的.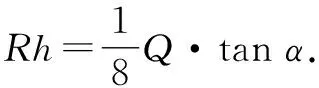

2.2 整体观察法
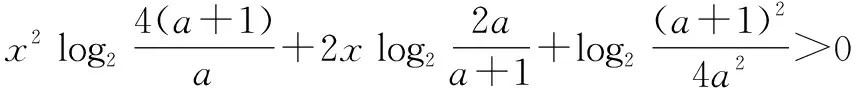

2.3 整体配对法
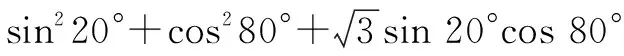


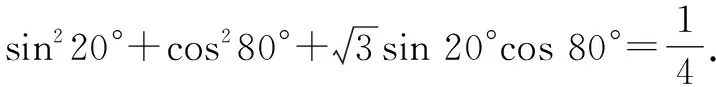

2.4 整体联想法
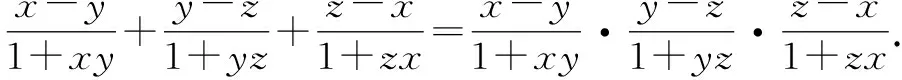
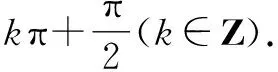

2.5 合设方程法



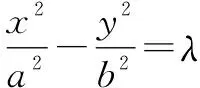

3 结论

