变换法在全等三角形解题中的运用
西华师范大学数学与信息学院 李佳洁 汤 强
1 引言
全等三角形的证明作为几何研究领域重要的一个分支[1],对学生逻辑思维和抽象转换能力有较高的要求.随着新课程改革,中考中出现的有关全等三角形证明的考题难度也在逐步提高,对题干信息的提取不仅仅局限于直接观察可得出,很多时候需要对图形进行变换,方可得到所需要的证明条件.因此,如何变换图形,转变已知条件为新的条件,成为学生在证明两个三角形全等的难点.本研究将以“变换法在全等三角形解题中的运用”为主题,针对初中生解全等三角形过程中可能会运用到的变换法进行系统整理归纳,并提出这些变换法对不同题型的应对策略,更好地帮助学生证明三角形全等[2].
2 变换法之一:轴对称变换
轴对称变换即将一个图形沿一条直线翻折得到它的关于轴对称的图形.通过轴对称变换得到的图形与原图形全等,并且二者的对应点连线与对称轴垂直平分,对应点到对称轴上任一点的距离相等[3].
例1如图1,在等腰直角三角形ABC中,AC⊥BC,AC=BC,线段BD为∠CBA的角平分线,问:线段BC,CD与AB有什么关系?

图1
分析:该问题中,由已知条件“线段BD平分∠CBA”引导学生想到轴对称变换,以BD为轴翻折△BCD使得C点与BA边上的点E重合,连接DE,从而由轴对称变换可得BC=BE,DE=CD,△BED≌△BCD,∠BED=90°;已知△ABC是等腰直角三角形,由其性质可得∠A=45°,DE=AE,等价代换有AE=CD,因此得到结论:BC+CD=AB.我们发现该题还可以运用截长补短来证明,但显然用截长补短的方法没有轴对称变换构造出的条件多,因此选择轴对称变换法极大地提高了解题效率.
结论:AB=BC+CD.
证明:如图2,已知线段BD平分∠CBA,将CB沿角平分线翻折后,令C落在线段AB上的对应点为E,由翻折可知△BED≌△BCD.
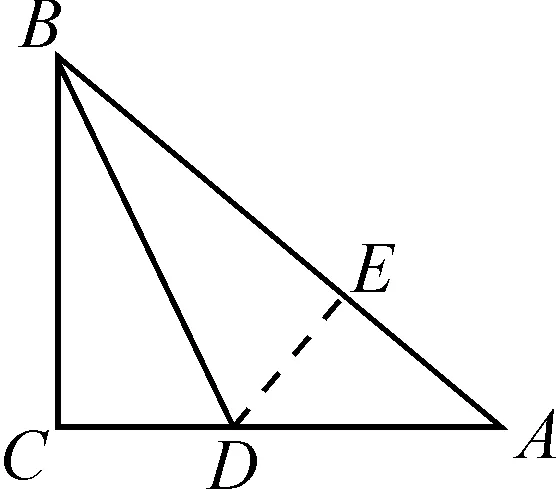
图2
∴CB=EB,∠CBD=∠EBD,
CD=DE,∠C=∠BED=90°.
∵△ABC是等腰直角三角形,AC⊥BC,
∴∠A=45°.
∴△ADE是等腰直角三角形,
∴AE=DE=CD.
又AB=BE+AE=BC+CD,
∴AB=BC+CD.
因此,线段BC,CD之和等于AB的长度.
3 变换法之二:中心对称变换
平面内使任意一对对应点A,A′的连线段都通过一个点O,且被这一点所平分,则该变换叫做中心对称变换(也称作反射或点对称).关于中心对称的两个图形全等,二者的对应点连线都经过对称中心且被对称中心平分,并且对应线段平行且相等.
例2△ABC中,AC=5,AB=7,求△ABC的中线AO的取值范围.
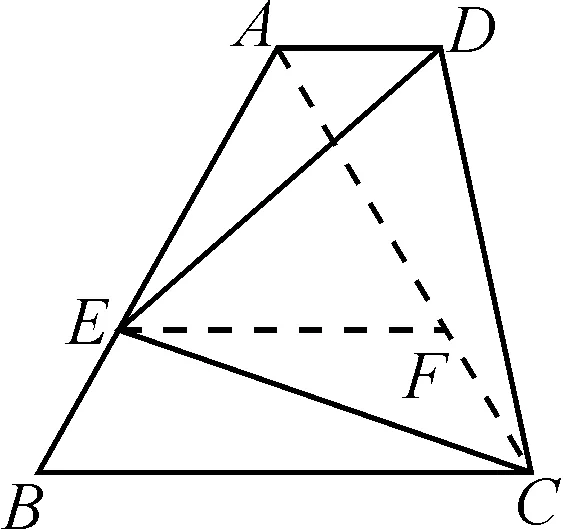
分析:凡是题干中出现“中线”“某线段2倍”这样的字眼,除了会想到用截长补短法,我们还可以运用图形的中心对称变换,如图3,将△ACO以点O为中心作中心对称变换,得到△EBO,则有△EBO≌△ACO,BE=AC.由三角形的性质定理可知,在△ABE中,AB-BE 图3 解:将△ACO以点O为中心作中心对称变换得到△EBO,则△ACO≌△EBO. 于是AC=BE,AO=OE. 又在△ABE中,AB-BE 所以AB-AC<2AO 即2<2AO<12. 因此,1 旋转变换作为一种重要的解题方法,通过将图形绕一定点旋转得到一个与之全等的图形.借用旋转变换的全等性,极大程度简化了解题步骤. 例3如图4,在ABCD中,A,E,D三点共线且AB=AE,过点E作直线EF,在直线EF上取一点G,使得∠BGE=∠BAE,连接GA,BG.FE与DC相交时,∠BAE=90°,求线段EG,AG,BG之间的数量关系. 图4 证明:如图5,将△AGE绕A点顺时针旋转90°,得△ABQ. 图5 ∴△AEG≌△ABQ, ∴∠GAQ=90°, AQ=AG, EG=QB,∠AEG=∠ABQ. ∵∠BGE=∠BAE=90°, ∴∠AEG+∠ABG=180°. ∴∠ABQ+∠ABG=180°. ∴Q,B,G三点共线. 又∵QG=QB+BG=EG+BG, 平移变换通过对平面图形按一定方向进行平移,得到新的图形,二者之间的对应边存在平行关系,对应点的连线也都平行.平移变换在初中几何解题中更多是对于平移变换思想的运用,如下题. 例4如图6,在四边形ABCD中,AD∥BC,点E是AB上一个动点,若∠B=60°,AB=BC,且∠DEC=60°,判断AD+AE与BC的关系,并证明你的结论. 图6 分析:通过连接AC,将梯形的问题转化为等边三角形问题.利用平移变换作平行线,根据已知条件和平行的相关性质定理,以及结合等边三角形的性质,通过证明三角形全等解决问题. 结论:BC=AD+AE. 证明:连接AC,过点E作EF∥BC,交AC于点F. ∵AB=BC,∠B=60°,EF∥BC, ∴△ABC与△AEF均为等边三角形. ∴∠AEF=∠AFE=∠EAF=60°,∠EFC=120°,AE=AF=EF. 图7 又∵∠DEC=60°, ∴∠AED=∠FEC. 又∵AD∥BC, ∴∠EAD=120°. ∴∠EAD=∠EFC. 又∵AE=EF, ∠AED=∠FEC, ∴△ADE≌△FCE. ∴AD=FC. ∴BC=AD+AE. 综上,我们可以发现,在全等三角形的解题过程中变换法相比截长补短、倍长中线等方法具有极大的优势,其中最明显的就是可以直接得出变换后的图形与原图形全等,从而简化解题步骤,使学生的数学逻辑思维更加清晰化.此外,在面对图形错综复杂、条件繁多的情况时,通过变换法可以使题中隐蔽的条件关系明朗起来,更容易找到解题途径.因此,巧用变换法证明三角形全等对学生而言是十分重要的.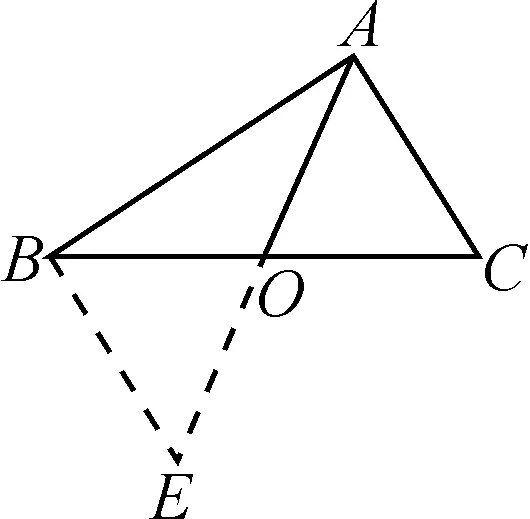
4 变换法之三:旋转变换
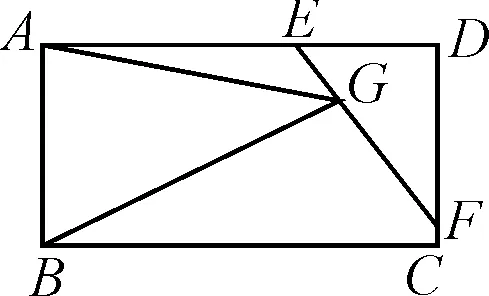



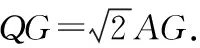
5 变换法之四:平移变换

6 结论

