例析几何问题中灵活变换线段的方法
天祝藏族自治县教育和科学技术局 王 斌
1 引言
图形转换出现在初中几何问题中时,通常表示该题对学生的解题要求较高,因为只有学生在灵活转换线段的前提下,才能更快地找到解题突破口.根据教学经验,变换图形中的线段通常有构造平行四边形、等腰三角形等方法.接下来,本文中结合几道例题谈一谈如何实现图形中线段的灵活变换.
2 图形中灵活变换线段的主要方法
有些图形的线段比较“散乱”,而要求解或证明这些线段之间的数量关系,无疑对学生产生了巨大困难[1].根据实际教学经验,发现图形中灵活变换线段的方法主要有以下几种.
2.1 构造平行四边形
例1如图1所示,在Rt△ACB中,∠C=90°,D,E分别为CB,CA延长线上的点,BE与AD相交于点P.BD=AC,AE=CD.试求∠APE的度数.

图1
分析:本题要求∠APE的度数,从图中观察这明显比较困难.但是,题中给出了“BD=AC,AE=CD”两个条件,提示解题者需要构造出全等三角形.然而,这些线段比较“散乱”,所以考虑构造平行四边形,将相关线段“集中”起来.本题构造平行四边形有两种方式,如下图2、图3.不难发现,图2中通过构造平行四边形之后,就将原本“散乱”的线段变换成关系更明朗的线段,在证明两个三角形全等之后易得等腰直角三角形ADQ,最后得到∠APE的度数为45°.图3中构造平行四边形的方式与图2相同,也是最终利用等腰直角三角形和平行四边形的性质得到∠APE的度数为45°.详细解答过程如下:

图2

图3
解法1:将BD,BE分别平移至EQ,DQ,使EQ,DQ相交于点Q,连接AQ,如图2所示.易得四边形BEQD为平行四边形.
∴CD//EQ,BD=EQ.
∵∠C=90°,
∴∠AEQ=90°.
∵BD=AC,
∴AC=EQ.
∵AE=CD,
∴△AEQ≌△DCA(SAS).
∴AQ=AD,∠AQE=∠CAD.
∴△AQD是等腰三角形.
∵∠AEQ=∠C=90°,
∴∠EAQ+∠AQE=90°.
∴∠EAQ+∠CAD=90°.
∴∠QAD=90°.
∴△AQD是等腰直角三角形.
∴∠ADQ=45°.
∵EB//QD,
∴∠APE=∠ADQ=45°.
解法2:将AD,AE分别平移至EQ,DQ,使DQ,EQ相交于点Q,连接BQ,如图3所示.易得四边形AEQD为平行四边形.
∴CE//DQ,AE=DQ.
∵∠C=90°,
∴∠BDQ=90°.
∵BD=AC,DQ=AE=CD,
∴△QDB≌△DCA,
∴BQ=AD.
∴BQ=EQ.
∴△EBQ是等腰三角形.
∵∠CDA+∠CAD=90°,∠QBD=∠CAD,
∴∠CDA+∠QBD=90°.
∵AD//EQ,
∴∠EQB=90°.
∴△EQB是等腰直角三角形,
∴∠EBQ=45°.
∴∠BPD=45°=∠APE.
2.2 构造等腰三角形
构造等腰三角形的方法比较多,常见的有旋转法、垂直平分线法等[2].下面结合例题对这两种不同的构造方法分别进行分析和说明.
2.2.1 旋转法
旋转法通常是将一边旋转至另一边,然后这边与所求证的边产生关联,进而得到最初两边之间的关系[3].这里仍以例1为例进行分析、说明.
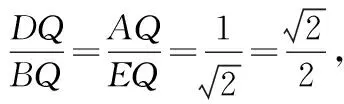

图4
2.2.2 垂直平分线法
垂直平分线法是根据垂直平分线的性质得到两条线段长度相等,可间接视为将一条边实现了变换.如下面的例2.
例2如图5所示,在△ABC中,BC=8,AB的垂直平分线交BC于点D,AC的垂直平分线交BC于点E,试求△ADE的周长.

图5
分析:本题中两条垂直平分线非常重要,因为可以借助它们将AD变换到BD,将AE变换到EC,进而将△ADE的周长问题转变为线段BC的长,这样一来问题就简单许多.具体过程如下:
解:∵AB的垂直平分线交BC于点D,AC的垂直平分线交BC于点E,
∴AD=BD,AE=CE.
∴△ADE的周长=AD+DE+AE=BD+DE+CE=BC=8.
3 变换线段时应注意的问题
线段变换是灵活解决初中几何中线段数量关系问题的重要方法,对学生的解题要求比较高.所以,在变换线段时需注意以下几个方面的问题:
首先,牢固掌握与变换线段有关的知识点,如平行四边形的性质和判定、垂直平分线的性质和判定、图形变换的性质、尺规作图等.同时,要在此基础上多训练,不断提升解题效率.
其次,变换线段位置的过程中,可能会产生更多的线段,会使原本的图形变得更加复杂[4].为了让学生分析得更加清楚,不至于在复杂的线段中“迷失”,可以借助彩色笔描绘的方法进行初步训练,将需要的线段或相等的线段、角等用彩色笔描绘,提高图形的辨识度.
4 结语
综上所述,灵活变换线段的位置,是有效解决一些复杂线段问题的重要方法.但是,这方面对学生的解题要求比较高.所以,作为一线数学教师,不仅要重视灵活变换思维的培养,而且要注意上述几个方面的问题,让学生拥有更强、更灵活的问题解决能力.

