借助波利亚解题思想发挥数学错题资源的价值

重庆师范大学数学科学学院 何 柳

1 引言

《基础教育课程改革纲要》指出，改革的具体目标之一是“使获得基础知识和基本技能的过程同时成为学会学习和形成正确价值观的过程”[1].这就需要教师转变传统“唯分数论”思想观念，多关注学生的学习兴趣与经验，引导学生学会学习.

2 错题资源化

在学习过程中，学生无可避免会出现错误.教师此时应当引导学生对错误进行归纳总结，从而将错题资源的价值最大化.

2.1 错题的分类及成因

2.1.1 知识型结构型错误

2.1.2 非知识结构型错误

(1)计算错误.随着知识难度提升，对学生运算能力的要求也相应提高.计算过程不只是单纯的运算，还需要对概念、公式和法则等进行灵活运用.(2)粗心错误.注意力分散、粗心，也是学生解题时错误频出的关键原因.部分学生由于粗心导致错误理解题目，混淆所需要求解的问题.精神不集中，导致代值计算时出现看错、抄错、写错等情况.(3)思维定势式错误.思维定式是根据内化的知识经验和已有的思维规律，在反复使用中养成的一种思维习惯.思维定式在数学学习中有其积极的一面，如掌握某类题型的“套路”，可以简化认知程序，节省解题时间.但更多的是消极的一面，其大大减少学生的创造能力和灵活变通意识[2].当题型稍加改变，学生易受思维定式影响而错解题目.

2.2 错题资源的利用

2.2.1 整理错题，培养归纳能力

在信息爆炸的时代，如何提取有用信息成为必需的技能.错题的整理可以培养学生归纳能力.从题目本身进行分类，深度挖掘题中考点，并由小及大引申出其他知识点；从错题产生原因进行分类，起到提醒作用，减少出错概率；从题目类型进行分类，总结方法规律，寻找高效解题方式，节省答题时间.也可以借助思维导图概括总结，加深知识点的掌握度和熟练度.

2.2.2 分析错题，找到薄弱点

教师要以包容的心态面对学生出现的错误.数学题目旨在考查学生对概念的理解、以及运算、逻辑等能力.引导学生对错题进行分析，找到存在的薄弱点，弥补自身不足，进行针对性复习.

2.2.3 结合错题，锻炼思维能力

数学是一门逻辑性极强的科学，由于思维能力的欠缺，做题过程中就易出现错误.例如一次函数y=kx+b的图象与k，b有关，部分学生由于概念混淆而导致思维混乱，因此不能根据函数图象性质解决问题.结合错题，教师可以引导学生理解数学中的内在逻辑结构，锻炼数学思维，形成数学逻辑；可以发散思维，将某一知识点进行扩充，体会知识点之间的联系.

2.2.4 订正错题，提升运算能力

运算能力薄弱也会导致学生错误频出.如在-18-(-3+5)-8+|8|的有理数混合运算中，面对多个负号、括号和绝对值，学生可能会出现计算逻辑混乱的情况.在订正错题的过程中，教师可以引导学生分析错解，梳理运算逻辑，养成严谨思维，不断提升运算能力.

2.2.5 回顾错题，加强反思能力

知识需要在不断回顾的过程中获得新启示.对错题进行回顾，可以起到警示作用，避免错误再发生.回顾运算错误，有利于梳理运算逻辑；回顾概念理解错误，有利于强化理解；回顾思维定式错误，有利于发散思维.

3 借助波利亚解题思想发挥错题资源的价值

匈牙利数学家波利亚在《怎样解题》中将解题划分为理解问题、拟定方案、执行方案、回顾四个步骤.这四个步骤环环相扣，指引着问题解决的方向.将波利亚解题思想融入到错题反思的全过程可以起到错误资源再开发的作用.

3.1 发挥价值的前提

中学数学更强调思维能力、辩证意识的培养，强调自主学习、学会学习.华应龙老师在化错教学中提出要充分挖掘并利用差错资源的多方面价值，培养学生直面错误、超越错误的求真人格，将教学活动引向学生内心深处，而不仅仅是促进认知的发展[4].师生需要转变以往对错误的偏激态度，以更加科学的眼光对待错误，关注对错误处理的过程，即看重从“错”到“对”这个思考分析的过程，并将错误作为一种促进学生发展的资源，提升学生的思辨能力.

3.2 发挥价值的具体步骤

3.2.1 再次审题，分析错误类型

通过波利亚解题思想可以得知，解题最主要的就是理解题目.因此，在回顾错题时，应重新理解题目，对错误类型进行分析.首先，判断是否由题目理解而导致解题错误；其次，判断是否由马虎而导致的错误；然后，推理整个分析过程，检验推理过程是否有不合理因素，判断是否有概念模糊等情况.根据错误的不同类型，采取不同侧重点，加深学生的印象.

3.2.2 制定方案，订正错题

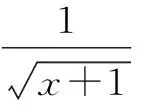
对较复杂的几何推理题，引导学生从需要求解的问题入手，逆推证明条件.例如：如图1，已知AC⊥AB，DB⊥AB，CE⊥ED，AC=BE，猜想线段CE与DE的大小关系，并证明你的结论.学生由于缺少证明全等的条件，而无法解决此题目.首先分析题目，我们可以得到，△CAE与△DBE均为直角三角形，明晰考查的是全等三角形证明的知识点，借助辅助问题引导学生回顾SSS,SAS,ASA,AAS,HL五种证明方法.题目中已有一边和一角对应相等，因此,我们可以从AAS,ASA和HL这三种方法考虑,再结合已知条件∠CED=90°，所以优先考虑AAS,ASA这两种证明方法.确定方法之后，就需要去寻找证明条件∠CEA=∠EDB或∠ECA=∠DEB.此时仅剩∠CED=90°这一条件，根据等量代换，可得到∠ECA=∠DEB.最后得到证明全等的三项条件，因此△CAE≌△EBD,所以CE=DE，并总结归纳此类一线三垂直模型.

图1

在寻找错题的解决方案过程中，教师可以指导学生从所求问题入手，借助波利亚解题过程中的辅助问题，将问题细分，结合已有的知识经验和已知条件，选取最合适的解决方案.方案制定完成后，严谨执行方案，避免错误的发生，真正做到大胆猜想小心求证.

3.2.3 反思回顾，总结规律

错题订正后，学生可以将正确与错误的解题方案进行比较，总结思想方法.首先,对错题的解决过程进行反思，例如错题类型、考查的知识点、渗透的思想方法等；其次，将错题按照单元或者错误类型等进行分类整理，并将错解和正解用不同颜色的笔誊抄完整，提高复习巩固效率.在阶段性学习结束后，要引导学生用思维导图的形式，复习所学内容，构建知识网络，培养学生举一反三的能力.