聚焦教材经典问题 明确几何教学方向——2021年北京中考几何题研题体会

江苏省扬州市江都区实验初级中学 韩 艳

1 引言

每年全国各地中考试卷多达几百份，而北京市中考试卷有着鲜明的首都风格.比如，重视“双基”，关注能力，善于创新，而且试题大气、新颖，没有偏题、怪题或者网络上流行的几何技巧、“大法”能够快速解决的“模型题”．笔者认真研习了2021年北京中考数学试卷，对该卷中的几何题有了一些初步思考和研题体会，梳理成文，与各为同仁研讨.

2 2021年北京中考几何题解读

题1如图1，PA，PB与⊙O相切于A，B两点．若∠APB=50°，则∠AOB的度数为.

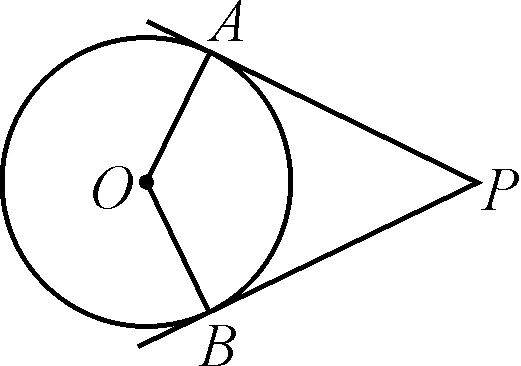
图1

解读：这个图形取材于教材中切线长定理的基本图形，该题属于考查“双基”的测试题．引导师生备考时重视教材上重要定理的基本图形，不需大量刷题就能掌握这类基础问题.

题2如图2，四边形ABCD是矩形，点E，F分别在边BC，AD上，且AF=EC．添加一个条件(写出一个即可)即可证明四边形AECF是菱形.

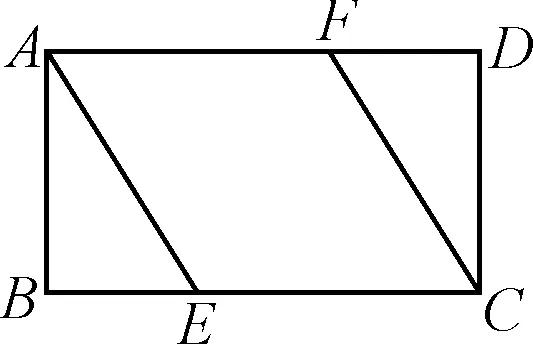
图2

解读：本题的图形也源于教材，以矩形为问题背景，让学生添加条件，使得平行四边形AECF强化为菱形.这是一个开放式问题，需要考生熟悉菱形的不同判定方法(需要先确认四边形AECF为平行四边形)，然后就可添加不同的条件.

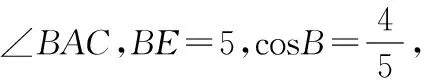
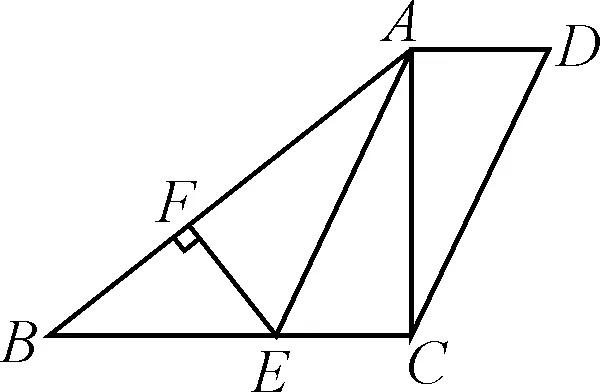
图3

解读：这道题综合了平行四边形的性质、“3，4，5”直角三角形、角平分线的性质等知识点，容易获得思路，关键是几何语句的规范表达.

题4如图4，⊙O是△ABC的外接圆，AD是⊙O的直径，AD⊥BC于点E．连接BO并延长，交AC于点F，交⊙O于点G，连接GC．若⊙O的半径为5，OE=3，求GC和OF的长.

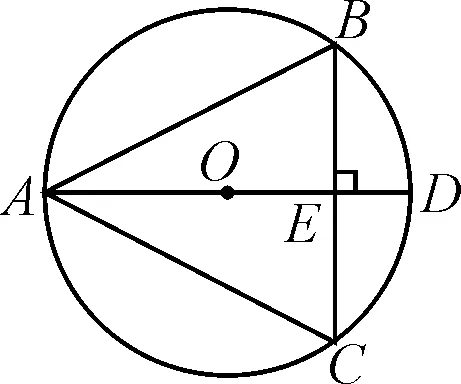
图4

解读：前面几道几何题都不需要添加辅助线即可解决问题，从本题开始，所给图形中的线段并不完整，需要结合题意补出图形(如图5)并求解(求解时，并不需要另外构造辅助线).作为圆的一道小综合题，涉及垂径定理、直径所对的圆周角为直角、相似三角形等知识点，属于一道中档题.

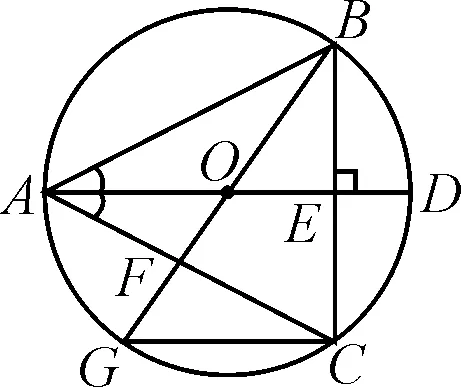
图5

题5如图6，在△ABC中，AB=AC，∠BAC=α，M为BC的中点，点D在MC上，以点A为中心，将线段AD顺时针旋转α得到线段AE，连接BE，DE．过点M作AB的垂线，交DE于点N，用等式表示线段NE与ND的数量关系，并证明.

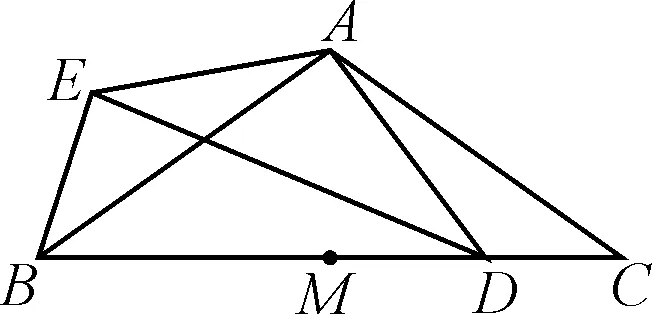
图6

解读：这是处于全卷倒数第二题的位置的几何综合题，是承载着选拔功能的一道大题．原题共两小问，第(1)问比较简单；限于篇幅，这里仅摘引了第(2)问，画出草图之后，容易猜想(直观看出)：点N是DE的中点．结合等腰三角形ADE的“三线合一”性质，解题的关键可转化为“证AN是△ADE的高”，结合图7，可证出∠AMN=∠ADN，从而确认A，D，M，N四点在同一个圆上，于是问题获得重要进展∠AND=∠AMD=90°.

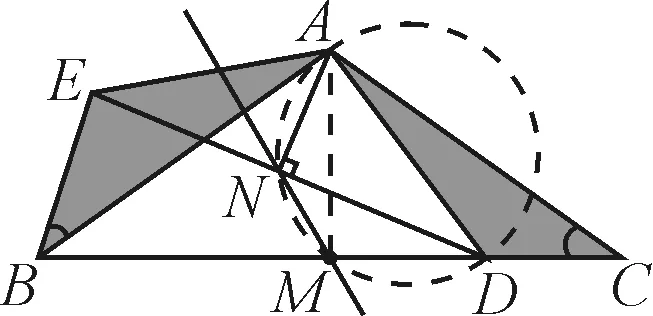
图7

此外，如图8、图9所示的构造辅助线也可以解决问题，限于篇幅，这里不再给出思路说明.

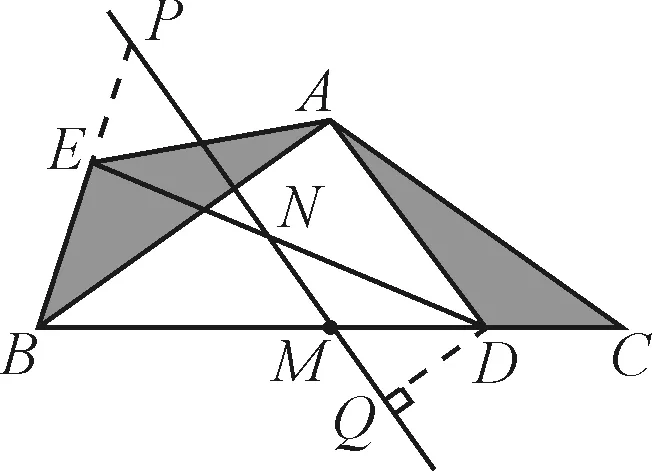
图8

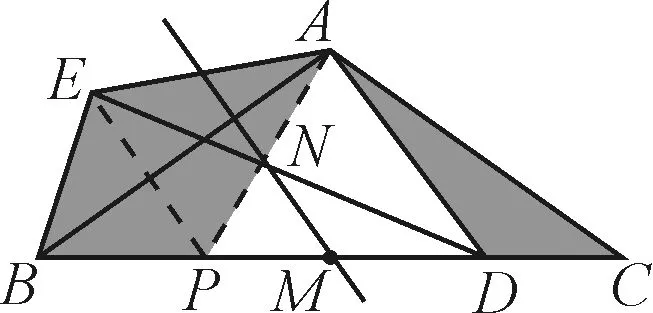
图9

3 北京中考几何题的教学导向之思

3.1 重视课本例题、习题的教学功能

由于网络技术、信息化的普及，每年全国各地几百份中考试卷及各地“名校”模考题往往在考试之后快速得到传播.一些搜题网站、APP及各类复习备考的教辅资料中，大量选用来自全国各地的这些考题，使得教材被“边缘化”.常常看到学生的教材基本不用，上课时只使用“集体备课”后的学案(习题集)，这种现象并不在少数，值得我们思考．从北京卷几何题的命题风格可以看出，北京中考几何题并没有那些偏题、怪题，也没有网传的很多模型或需要较高构造技巧的最值问题，这给我们带来的教学导向就是，要重视课本例题、习题的教学，不论是新授课还是复习课，都要扎实做好教材上例题、习题的教学与研究.

3.2 围绕经典图形问题教深教透

深度教学是近年来很多专家倡导的教学追求．比如，南京大学哲学系郑毓信教授认为深度教学要追求教学内容的深度、广度和贯通度．具体到解题教学，就是要努力让学生做一题，会一类，通一片[1]．从北京卷出现的以上几何图形来看，全部都是经典图形，即不管教材几经修订，这些经典图形几十年来始终出现在课本中，我们在教学中要十分重视它们的教学价值，教师本人不能误认为自己太熟悉了，没有什么可讲的，就带领学生“一闪而过”，接着刷大量的所谓变式题、同类题．学生对一些经典图形的“标准问题”还没能深刻理解，就急于变式、刷题，往往事倍功半．顺便提及，《中学数学》(初中版)近年来刊发了不少围绕经典图形问题研发的“一图一课”课例文献，也是将经典问题教深教透的积极实践，值得我们学习和践行[2].

3.3 解后回顾、揭示深层结构

针对经典图形的深度教学需要有解后回顾反思的环节，这是波利亚解题理论的重要环节．根据教学经验，在一个典型问题教学设计中，能否预设有效的解后小结往往能鉴别初任教师和专家教师的解题教学的专业基本功[3]．就本文中关注的经典图形问题来说，解题教学不只是关注一题多解，更重要的是思考“多解归一”，并善于帮助学生揭示问题的“深层结构”.比如，上文题5讲评之后，要让学生多看几眼图7，并想清辨明图7是如何画图、渐次生成的，能否由这幅图出发，写出它的题设或条件，然后证出哪些结论，这些结论中哪些是“等价”结论(可以快速“成果扩大”得出).

3.4 解题教学要让学生学会解题

涂荣豹教授指出：数学解题教学的任务，实际上是要教学生“学解题”[4]．所谓“学解题”，就是要让学生学会思考如何解题，而不只是满足于获得某一道具体例题、习题的解法或答案．这就要求我们精选好的问题、经典图形问题，从习题教学走向问题驱动，“拉长”学程，让学生对某类经典问题的求解从“快思”走向“慢想”.只有平时对某一经典问题“长时间思考”，获得这类问题的深刻理解，学生将来在考场上再遇到这类问题或同类问题时，才能用较短时间识别或看清问题本质，快速转化为自己熟悉的“等价问题”，从而获得思路的贯通.

4 写在后面

中考命题是以国家课程标准为命题原则，追求试题育人，指向课堂，回归教材，特别是注重从教材中挖掘和选用背景材料，让重视教材的师生“沾光”，让过度选用课外资料大量刷题的师生事倍功半．从这个角度看，本文关注的北京卷的几何题基本达到了上述要求，值得我们深入研习.对于很多承担着区域命题任务的老师来说，是不是也应该以北京卷作为一面镜子，“照照”自己命制的试卷，看看我们的命题方向、命题立意是否合适，是否出现了“喜好偏向”呢？