动中求定 四招搞定
⦿江苏省淮安市钦工中学 葛美云
1 引言
解析几何中的定值、定点、定圆和定直线“四定”问题,是新课标高考的命题热点,也是考生高考复习的难点.由于这类问题涉及面广、综合性强,方法又灵活多变,令“无数考生竞折腰”.常言道:兵来将挡,水来土掩.那么,破解这类问题有无良策呢?
2 利用定义
二次曲线的定义中就隐藏着“定元素”,如椭圆上的点到两个定点的距离之和是定值,抛物线中动点到定点的距离等于定直线的距离,这些“定元素”,如果能够为我所用,则会大大优化证明过程.
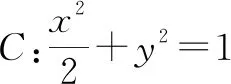
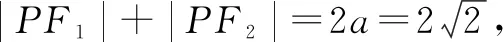
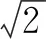
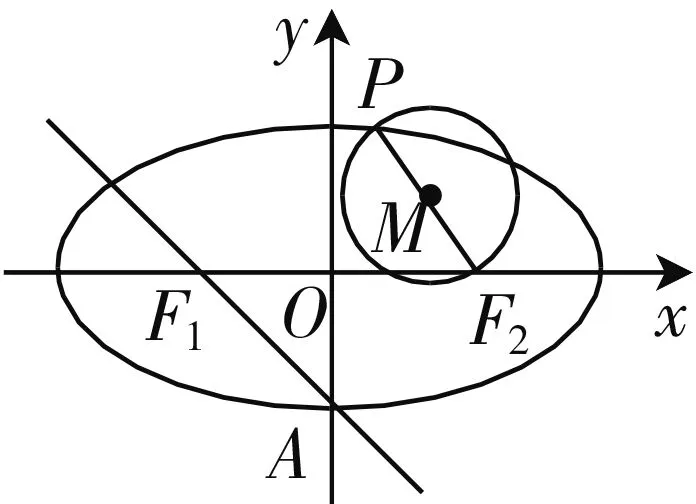
图1
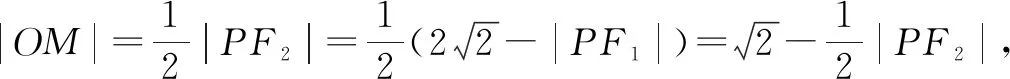
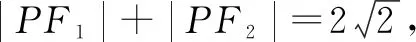
3 设参消参
为了方便解决问题,我们往往采用设而不求的思想方法,先设出含有多个参数的直线方程或点的坐标,然后用这些参数表示目标代数式,再利用参数满足的关系式,即可得到目标代数式为定值.

分析:显然直线AB的斜率存在,设其方程为y=kx+b,与双曲线方程联立,因为它们相切,所以判别式Δ=0,于是得到k与b之间的关系式;再联立直线AB与渐近线的方程,计算x1x2与y1y2的值.
解:设直线AB的方程为y=kx+b,b>0.

由于直线AB与双曲线相切,所以k2-3≠0,Δ=(2kb)2-4(k2-3)(b2-3)=0,即k2+b2=3.
设A(x1,y1),B(x2,y2),y1>0,y2>0.
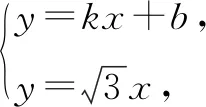


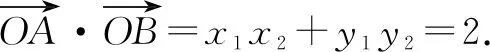
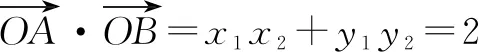
4 特值探路
有了目标,解题才有方向.为了寻找定值,解题时可以采用特值法.通过直线的特殊位置或点的特殊位置,先找出题目中要证明的“定元素”,然后利用题目条件加以证明.

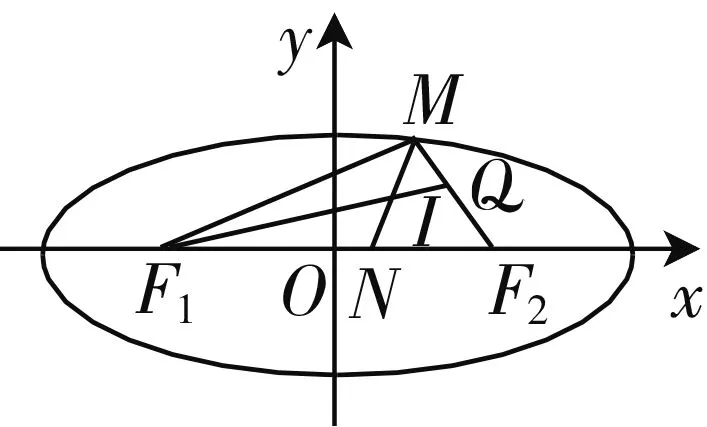
图2

证明:先取点M在y轴上,由角平分线性质得
设M为椭圆上任一点,F1Q交MF2于点Q.
设|MF2|=m,则|MF1|=2a-m.
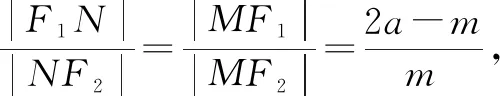

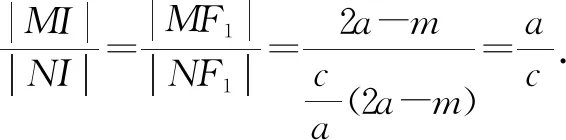
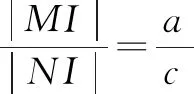
点评:特值法探路,是这类问题最基本的解题策略.利用特殊点或特殊位置进行计算,从而找到证明目标.而在推证过程中,将特殊化为一般,按照特值法的运算步骤重新加以演算,在演算中或采用设而不求的方法,或采用整体代换的方法,依据有关条件,参数自然消去,从而得到定值.若在计算中无法消去参数,则往往运算有误,可以认真检查,及时纠正错误.
5 方程思想
通过设而不求,将所涉及的方程罗列出来,然后将这些方程左、右两边同时相加减或乘除,有时会收到意想不到的效果,比如与中点弦有关的点差法,整体代换能让复杂的解题过程“峰回路转,柳暗花明”.
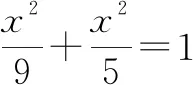
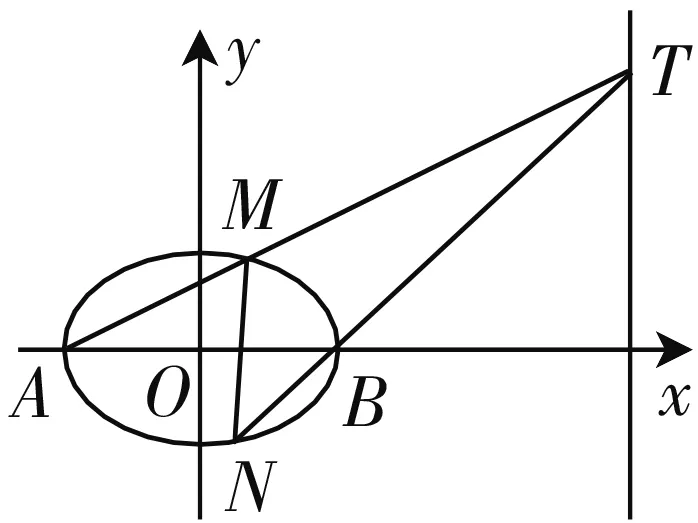
图3

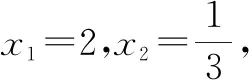
(3)设t=9,试证:直线MN一定经过x轴上某个定点.
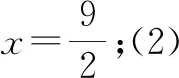
证明:设MN与x轴的交点为D.
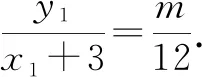
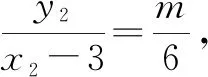
整理得2x2y1-6y1=x1y2+3y2.
①

整理得2x1y2-6y2=x2y1+3y1.
②
由①+②,得x2y1-x1y2=y1-y2.
若x1=x2,则y1≠y2,所以x1=x2=1,直线MN过点D(1,0);
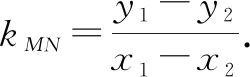
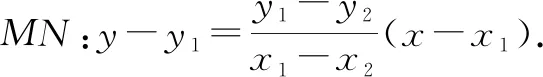
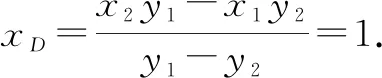
综上,直线MN过定点D(1,0).
点评:解析几何中两曲线的交点问题,通常采用设而不求的方法处理,从而规避烦琐的解方程组过程.我们往往先将有关点的坐标设出,然后找到这些点与某些方程之间的关系,进而利用韦达定理或点差法整体代换,不但代数运算简便了,还可以减少计算中的失误.
6 结论
从以上解析几何中的“四定”问题来看,要减少计算量,首先必须明确目标,其次要选择恰当的方法,再次就是以顽强的毅力将计算进行到底,而最关键的就是方法的合理选择.

