“一般观念”指引下的立体几何教学设计
——以“直线与平面垂直的性质”为例
⦿福建省福安市第一中学 阮金锋
1 内容解析
直线与平面垂直是直线与平面相交位置关系中的一种特殊情况,它是空间直线与直线位置关系的拓展,又是平面与平面垂直的基础.直线与平面垂直的性质定理是直线与平面垂直的必要条件,就是在直线l与平面α垂直的条件下,直线l、平面α与空间中其他直线、平面的位置关系.一条直线垂直于一个平面的必要条件很多,直线与平面垂直的性质定理解释了空间中直线、平面的“平行”与“垂直”之间的内在联系.
2 目标解析
(1)能够类比直线与平面平行性质定理的学习过程,说出直线与平面垂直的性质,如何研究直线与平面垂直的性质;
(2)会证明直线与平面垂直的性质定理,感悟“正难则反”的证明思路,感悟“平行”与“垂直”的相互转化.
3 教学问题诊断分析
虽然学生有直线与平面垂直的生活经验和感知,但他们把空间问题转化为平面问题的意识和能力还不强.因此,在线面垂直的条件下,探究有什么结论,会遇到困难.对于直线与平面垂直性质定理的证明,用反证法学生不易想到,怎么适当引导也很重要.
4 教学重点、难点
教学重点:直线与平面垂直的性质定理.
教学难点:直线与平面垂直的性质定理的探究.
5 教学过程
5.1 回顾旧知,明确路径
师:前面我们学习了3个判定、2个性质.线面平行的判定、性质,面面平行的判定、性质,线面垂直的判定,接下来该学习什么?
生:线面垂直的性质.
师:线面垂直的性质该怎么研究,有怎样的研究路径?能否类比前面学习的两个性质,找到研究路径?让我们先从直线与平面平行的性质定理说起.回顾直线与平面平行的性质定理,将下列表格(表1)补充完整,并思考性质的研究路径.

表1
师:直线与平面平行的性质定理,研究的是在线面平行的条件下,能推出怎样的结论.但仅有线面平行一个条件不够,肯定要增加条件,引进几何量.增加怎样的条件?引进哪些几何量?
生:直线与平面平行的性质定理,在线面平行的条件下,引入几何元素“线”,也可引入“面”.
师:你能举个这样的例子吗?
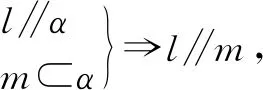
师:类比前面探究思路,线面垂直的性质该如何研究?研究路径怎么确定?
生:线面垂直的性质,就是在线面垂直的条件下,探究有什么结论?为了得到结论,也是引入几何元素(线或面).
师:你能举个引入直线的例子吗?
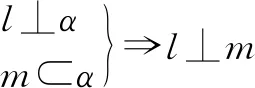
师:还能得到其他性质吗?
设计意图:以“一般观念”引领教学,明确线面平行性质的研究路径:在线面平行的条件下,探究有什么结论.通过类比,确定线面垂直性质的具体研究路径为:在线面垂直的条件下,引入几何元素(线或面),探究有什么结论[1].这样的研究路径,形成学习的基本套路,将有助于面面垂直的性质研究,真正提升数学研究水平,有利于后续的学习.
5.2 操作探究,提出猜想
活动1:小组讨论,根据线面垂直的研究路径,在线面垂直的条件下,引入几何元素(线、面),怎么探究线面垂直的性质?你能否列举出一些例子?
学生展示.(提示学生,利用教具演示)上台列举增加几何元素后线面垂直的性质的例子.
设计意图:注重发挥学生的主体性,学生的参与率相当高.教具观察、教具演示、都站在学生的认知角度,让学生积极参与小组讨论、上台展示交流、互动.真正落实学生为主体的教学理念.
活动2:根据以上研究路径,为了研究直线与平面垂直的性质,完成以下探究实验.把下列表格(表2、表3)补充完整,提出猜想,并扫描二维码,借助网络画板进行操作确认.
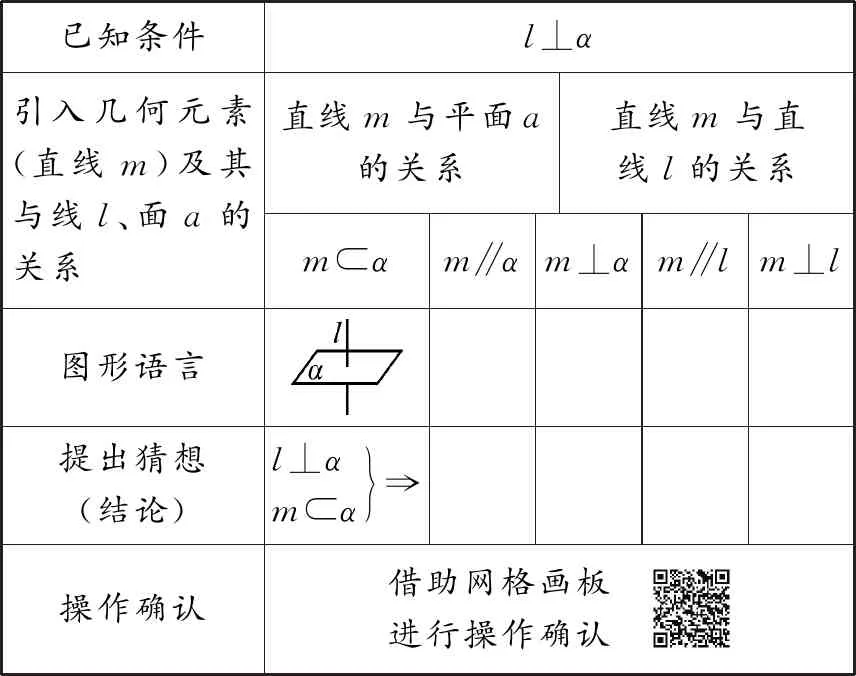
表2
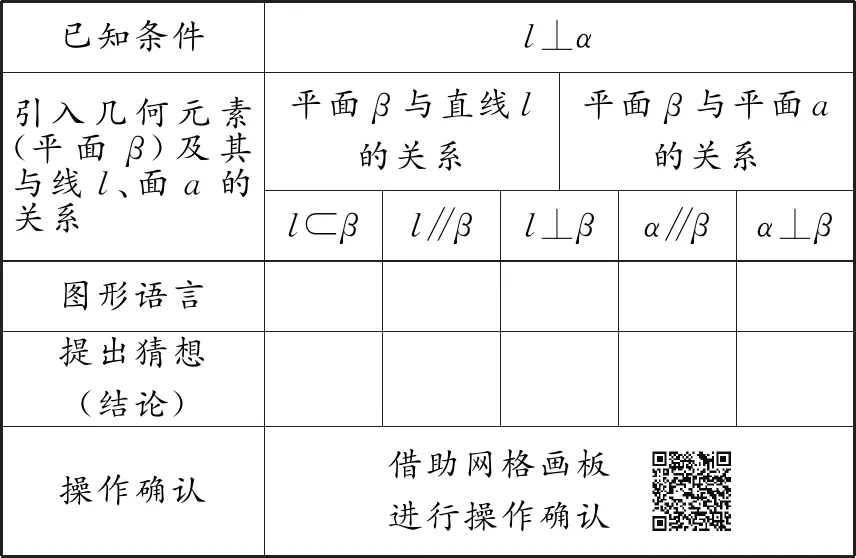
表3
在线与面垂直的条件下,引入几何元素(线m).
在线与面垂直的条件下,引入几何元素(面β).
设计意图:在探究线面垂直性质方法的指引下,引导学生在空间中引入一条直线m或者一个平面β,结合l⊥α,探究有什么结论(重点研究平行和垂直的位置关系)?通过小组合作、操作验证完成探究活动,并填写实验记录表.
有了“一般观念”的引领,选择数学实验活动的探究方式,再借助实物操作、网络画板3D平台,让学生按照一定的逻辑来探究直线与平面垂直的必要条件,经历直观感知、操作确认的过程,积累丰富的数学基本活动经验[2].
5.3 证明猜想,获得定理
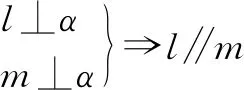
已知l⊥α,m⊥α,求证l∥m.
直线与平面垂直性质定理的证明要用到反证法,要在如何想到用反证法、为什么用反证法上加以引导,克服难点.引导学生根据定理的条件,从正面入手进行分析,暴露思维过程.
设计意图:在”一般观念”的指引下,得到一些线面垂直性质的有关猜想,接着证明猜想,获得定理.这符合立体几何学习中的“直观感知—操作确认—思辨论证”认知规律.
5.4 定理运用,巩固提升
例题已知平面α,β,且α∩β=l,CA⊥α,CB⊥β,A,B是垂足,A∈α,B∈β,m⊂α,m⊥AB.求证m∥l.
设计意图:对性质定理进行简单应用,加深学生对线面垂直性质定理的理解.在学生独立思考后,教师进行引导,再由学生独立完成.运用定理,巩固提升.
6 教学反思
本设计以“一般观念”引领教学,体现大单元教学设计观,是课标理念的具体要求,用系统的思想进行整体设计,符合数学学科特点,有利于构建知识体系.通过“直观感知—操作确认—思辨论证”认知过程展开,对教具图形的观察(直观感知)与实验探究(操作确认)发现和提出线面垂直条件下的有关命题,在经历观察、实验、猜想等合情推理的活动后,概括出线面垂直的相关性质,再对其中的性质定理进行证明论证(思辨论证).能认识到线面平行性质、面面平行性质、线面垂直性质探究路径的一致性,提升直观想象、逻辑推理核心素养[3].

