数学抽象视角 核心素养引领
⦿安徽省合肥一六八中学 张 禹
1 引言
数学抽象是数学新课标中创新性指出的六大核心素养之一,是指舍去数学问题的一切外在的物理属性,进而揭示数学问题本质与数学研究对象的一种基本素养.数学抽象是借助多个层面的视角,综合问题情境抽象出问题的一般规律和结构等,应用数学语言予以表征,为数学问题的解决提供条件,是贯穿于整个数学教学与学习的一条隐形、思维性的链条.下面结合2021年高考数学真题,从多个视角层面,合理抽象出数学的概念、命题、方法和体系,阐述数学抽象的培养与渗透方法,引领与指导数学教学与学习,抛砖引玉.
2 借助创新定义进行数学抽象
例1(2021年高考数学新高考Ⅱ卷第12题)(多选题)设正整数n=a0·20+a1·21+……+ak-1·2k-1+ak·2k,其中ai∈{0,1},记ω(n)=a0+a1+……+ak,则( ).
A.ω(2n)=ω(n)
B.ω(2n+3)=ω(n)+1
C.ω(8n+5)=ω(4n+3)
D.ω(2n-1)=n
分析:根据创新定义进行数学抽象,借助相应的创新公式,结合各选项中的取值情况合理分析.
解析:由于2n=a0·21+a1·22+……+ak-1·2k+ak·2k+1,则有ω(2n)=ω(n)=a0+a1+……+ak,故选项A正确;
当n=2时,2n+3=7=1·20+1·21+1·22,可得ω(7)=3,而2=0·20+1·21,则有ω(2)=0+1=1,所以ω(7)≠ω(2)+1,故选项B错误;
由于8n+5=a0·23+a1·24+……+ak·2k+3+5=1·20+1·22+a0·23+a1·24+……+ak·2k+3,可得ω(8n+5)=a0+a1+……+ak+2,
而4n+3=a0·22+a1·23+……+ak·2k+2+3=1·20+1·21+a0·22+a1·23+……+ak·2k+2,
所以ω(4n+3)=a0+a1+……+ak+2=ω(8n+5),故选项C正确;
由于2n-1=1·20+1·21+……+1·2n-1,可得ω(2n-1)=n,故选项D正确.
故选择答案:ACD.
点评:信息创新的多选题,往往借助创新信息给出合理创设,解决此类问题的关键是合理分析与理解相关题目条件中的创新信息,理解与掌握“新信息”的实质,借助数学抽象得出新概念、新公式、新运算、新方法、新对应法则等创新元素,用合适的数学思维与方法去理解与应用“新信息”要素,挖掘隐含其中的数学基础知识、思想方法和基本技能等,合理转化,巧妙应用.
3 借助数学公式进行数学抽象
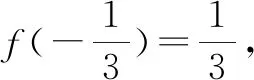
分析:合理借助题目条件中的奇函数的性质以及抽象函数的关系式f(1+x)=f(-x),加以数学抽象,通过逻辑推理与转化,确定函数的周期性,再结合所求函数值加以变形与转化,进而得以逻辑推理与化归.
解析:由于f(x)是定义域为R的奇函数,则有f(-x)=-f(x).
结合f(1+x)=f(-x),可得f(1+x)=-f(x).
所以f(x+2)=-f(x+1)=f(x),即函数f(x)是周期为2的周期函数.
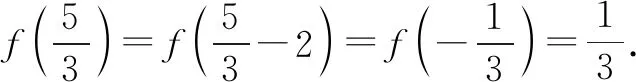
故选择答案:C.
点评:借助奇函数的性质结合抽象函数奇偶性的定义,并利用抽象函数所满足的关系式加以数学抽象,进而有效合理转化与变形,确定抽象函数的周期是破解的关键一环,在此基础上进行合理变形,巧妙求值.
4 借助性质特征进行数学抽象
例3(2021年高考数学上海卷第12题)已知ai∈N*(i=1,2,……,9),对ak=ak-1+1或ak=ak+1-1(2≤k≤8)中有且仅有一个成立,且a1=6,a9=9,则a1+a2+……+a9的最小值为________.
分析:基于对题目条件的直观理解,结合任意相邻三项中仅有两项是相邻正整数,从数列中相关项的性质特征视角切入,结合数列从前到后(或从后到前)的不同情况分类讨论,逐一确定数列中各项的取值情况与相互数量关系,进而加以求和处理,通过各项的取值条件确定对应的和式的最小值,比较两者不同情况下所得的最小值,即可得所求的答案.
解析:由题可知,任意相邻三项中仅有两项是相邻正整数.
(1)若a2=a1+1=7,则a3≠8,a4=a3+1,a5≠a3+2,a6=a5+1,a7≠a5+2,a8=a7+1.
所以a1+a2+……+a9=6+7+a3+(a3+1)+a5+(a5+1)+a7+(a7+1)+9=25+2(a3+a5+a7)≥25+2(1+1+1)=31,此时a3=a5=a7=1,a4=a6=a8=2时取等号.
(2)若a8=a9-1=8,则a7≠7,a6=a7-1,a5≠a7-2,a4=a5-1,a3≠a5-2,a2=a3-1.
所以a1+a2+……+a9=6+(a3-1)+a3+(a5-1)+a5+(a7-1)+a7+8+9=20+2(a3+a5+a7)≥20+2(2+2+2)=32,此时a3=a5=a7=2,a4=a6=a8=1时取等号.
综上所述,a1+a2+……+a9的最小值应该是31.故填答案:31.
点评:通过数列中相关项的性质特征分析处理,充分领会题目创新定义的实质,抓住数列对应项之间的关系建立关系式.正确分析题意,抽象出问题的性质特征,这是破解此类问题的关键所在.
5 借助图形直观进行数学抽象
例4(2021年高考数学全国甲卷文、理科第2题)为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图,根据此频率分布直方图,下面结论中不正确的是( ).

A.该地农户家庭年收入低于4.5万元的农户比率估计为6%
B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C.估计该地农户家庭年收入的平均值不超过6.5万元
D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
分析:利用频率分布直方图中频率的求解方法,通过直观图形加以数学抽象,进而求解频率即可判断选项A,B,D,利用平均值的计算方法,即可判断选项C.
解析:对于选项A,该地农户家庭年收入低于4.5万元的农户比率约为(0.02+0.04)×1×100%=6%,故选项A正确;
对于选项B,该地农户家庭年收入不低于10.5万元的农户比率约为(0.04+0.02×3)×1×100%=10%,故选项B正确;
对于选项C,估计该地农户家庭年收入的平均值为3×0.02+4×0.04+5×0.1+6×0.14+7×0.2+8×0.2+9×0.1+10×0.1+11×0.04+12×0.02+13×0.02+14×0.02=7.68>6.5,故选项C错误;
对于选项D,家庭年收入介于4.5万元至8.5万元之间的频率约为(0.1+0.14+0.2+0.2)×1=0.64>0.5,故估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间,故选项D正确.
综上分析,故选择答案:C.
点评:该题以我国脱贫攻坚工作取得全面胜利和农村振兴为背景,通过图表给出了某地农户家庭收入情况的抽样调查结果,以此设计问题进行数学抽象,考查频率分布直方图的应用,以及分析问题的能力与数据处理能力,解题的关键是掌握频率分布直方图中频率的求解方法以及平均数的计算方法.
6 借助方法归纳进行数学抽象
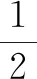
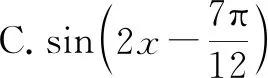
分析:合理分析题目情境,抓住实质进行数学抽象,通过三角函数问题的逆向思维,利用三角函数图象的平移变换的逆向操作过程来分析与处理,进而得以确定原三角函数的解析式.
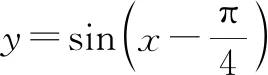
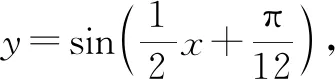
故选择答案:B.
点评:根据题目条件进行数学抽象,采用逆向思维,结合三角函数的图象平移变换规律加以分析,分步处理,一步一步到位,合理化简,思路自然,解法常规.方法技巧合理科学,思维方法简捷.
借助高考真题实例多视角层面展示,在数学教学与学习中,数学抽象能合理有效抽象出相应的数学概念、公式、命题、性质、图形、方法和思维体系等,养成分析问题、思考问题、探究问题等的一般性习惯,进一步归纳总结,有效把握数学问题的本质属性,全面抽象概括、以简驭繁,进而有效借助数学抽象的核心素养与思维方式来思考、分析与解决问题,优化思维品质,提升数学能力.

