数学分析课程对学生创新应用能力的培养——以多元函数微分学应用为例

■ 湖南工商大学理学院 邓小青 张 健 陈建文

《数学分析》课程是信息与计算科学专业和数学与应用数学专业的专业主干课程,能力培养尤其是创新能力培养是本科教育的根本目的之一。数学概念和数学原理的理解有利于创新能力的提高,数学思想及数学方法的掌握更是创新的源泉和发展的基础,也是数学能力的集中体现。对重要的数学概念、原理和思想方法,一定要反复体会和深入思考,试图从各个侧面,各个角度去解剖分析,加深理解,真正达到融会贯通,清晰明了。只有对数学概念、原理的透彻的理解,才会有得心应手的应用,乃至出人意料的创新和发展。在数学分析教学中,注重数学概念和数学原理的理解、注重数学思想方法的掌握、注重数学知识的应用,引导大学生自觉投入各种有趣的科技创新活动中去,无疑会对他们的创新能力提高起到事半功倍之效。

数学分析的计算方法和技巧具备多样性和灵活性,我们在教学过程中要善于把握这个特点,在教学中紧扣一题多解,充分利用已有知识点,启发学生从多个角度去思考问题,归纳总结出多种方法,培养学生殊途同归、学以致用和不怕困难的精神,从而提高创新应用能力。

1 已有结论

(1)若曲面Σ的方程为F(x,y,z)=0,则曲面Σ在点(x0,y0,z0)的切平面为:

F′x(x0,y0,z0)(x-x0)+F′y(x0,y0,z0)(y-y0)+F′z(x0,y0,z0)(z-z0)=0

2 一题多解

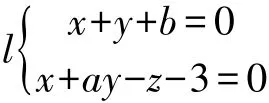
启发学生结合直线方程、平面方程、切平面方程的计算公式、直线与平面关系等知识点,从不同的角度去分析和解决该问题。

式中，Ct为施药后第t天的农药残留量(mg/kg)，C0为原始沉积量(mg/kg)，k为降解速率常数，t为施药后时间(d)

5.入股分红模式。河南民兴生物科技有限公司与330户建档立卡贫困户签约，保证每年分红不低于3200元。镇平县新奥针织公司投资2200万元，在10个贫困村建立扶贫车间，吸纳贫困群众就业，实现人均年增收15000元。

解法1:曲面z=x2+y2在点 (1,-2,5)处的切平面为2(x-1)-4(y+2)-(z-5)=0,即平面Π 2x-4y-z-5=0。又直线的方向向量为,由于,故由知a=-5。在直线上取一点 (-b,0,-b-3),代入平面方程得b=-2。

名物化(nominalization)，又译作名词化或名化，是一种语言语法化现象，在英语各种文体中普遍存在，但使用方式不一。名物化研究可以从词汇层面、句法层面和语篇层面开展。以往的研究大多集中在词汇层面和句法层面，近年来随着国内英语名物化研究呈现系统功能语言学和认知语言学转向[1]61，以语篇为单位考察名物化现象的研究日渐增多。

解法2:曲面z=x2+y2在点(1,-2,5)处的切平面为2(x-1)-4(y+2)-(z-5)=0,即平面Π 2x-4y-z-5=0。

3.打好“和谐牌”，提升凝聚力。要始终把实现好、维护好、发展好最广大人民的根本利益作为党和国家一切工作的出发点和落脚点。如何落实？“和谐牌”给出答案——要深入持久地开展“合作”活动，全方位、多角度地搭建合作沟通平台，并突出抓好“信息交流、人性化管理、约束激励”这三个机制建设，重点在“意识、质量、成效”等三个环节上做文章，从而让“沟通、信任、尊重、宽容”为核心的合作理念深入人心并能付之实践，实现合作宽度、深度的持续拓宽与加深，有效促进和谐发展氛围的形成。

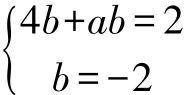
方法3点击:曲面的切平面容易求出来,因为直线在该平面上,所以直线上任一点都在该切平面上,故该直线和切平面联立求解,对应方程组有无穷多解,根据线性方程组解的判定定理解题。

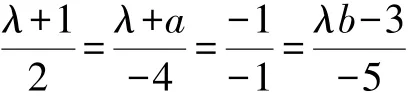
解法3:曲面z=x2+y2在点(1,-2,5)处的切平面为2(x-1)-4(y+2)-(z-5)=0,即平面Π 2x-4y-z-5=0。

统计数据显示，由于日本和中国的关系经常紧张，很多日本游客会优先选择韩国作为出行首选。而2013年，中国超过日本首次成为韩国的最大外国游客来源国。韩国接待外国游客的数量连年保持双位数百分比增长，在旅游旺季，首尔酒店的入住率可达到约90%，要想找到低价酒店只能驱车远离市中心上百公里。

方法2点击:曲面的切平面容易求出来,因为直线在该切平面上,所以直线上任一点都在该切平面上,找两点即可解题。

方法4点击:曲面的切平面容易求出来,因为直线在该切平面上,该切平面是经过该直线的平面束中的某一平面。

大脑、肝脏、心脏等三种器官是动物体内中枢器官和最重要的物质代谢器官，同时肝脏又是合成GSH的重要器官，在机体衰老过程中，大脑、肝脏、心脏中的GSH含量均出现显著的下降趋势，因此通过检测这三种器官中GCL和GSH含量可以反映机体抗氧化反应和清除自由基能力。白藜芦醇属于非黄酮类多酚化合物，是葡萄、桑葚、虎杖等许多种植物在遇到不利环境时自然产生的一种植物抗毒素，研究发现，白藜芦醇能够延长机体的平均存活时间，延长正常的生命周期[9]。

方法5点击:曲面的切平面容易求出来,因为直线在该切平面上,故该直线的参数方程满足切平面方程。

她的房间在二楼，窄小单人房间，墙角放置一只纯黑色压荔枝纹牛皮行李箱，很旧，但款式经典品质精美，整张厚牛皮散发温润光泽，抚摸时有紧绷的弹性。她说这是她与母亲以前在欧洲跳蚤市场买的二手货，在旅途中使用时久日长。最后到她手里。她去伦敦读书，带着这只箱子，放了一些简单衣物和书籍。

解法5:易知曲面z=x2+y2在点 (1,-2,5)处的切平面为平面Π: 2x-4y-z-5=0。

2.3.5 SaO2 纳入4篇文献，各研究间存在异质性（P＜0.000 1，I2=90%），采用随机效应模型进行Meta‐分析，见图5。结果显示治疗前后试验组SaO2增加值显著大于对照组，差异有统计学意义［MD=5.32，95%CI（3.14～7.50），P＜0.000 1］。

方法1点击:曲面的切平面容易求出来,又因为直线在该切平面上,所以直线的方向向量垂直于该切平面的法向量,且直线上任一点都在该平面上,找一点即可解题。

该例题看起来简单,但学生有好几种解法,说明学生对数学知识的掌握情况不一样、数学思维不一样、解法就不一样。数学知识掌握扎实的同学,思维活跃,不循规蹈矩。当然也不排除,有些学生对隐函数不理解,停留在显函数的导数与偏导数层次,试图考虑先将隐函数转化为显函数的方法。该题的常规解法是直接利用隐函数定理,下面列出常规解法和其他解法。

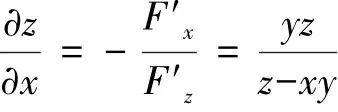
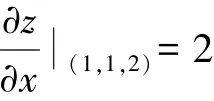
解法3:由于z2-2xyz=a是曲面方程,依据题意,点(1,1,2)在该曲面上,于是a=0。由于z2-2xyz=0,所以(z-xy)2=x2y2,即。又注意到隐函数的连续性,在点(1,1,2)附近,x,y,z＞0,所以上式取正,于是。

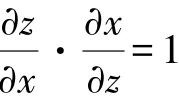
解法2、解法3和解法4虽然把简单的问题复杂化,但是体现了学生的创新意识和活跃的思维,敢于尝试、敢于创新、敢于打破常规。

3 结论

能力比起单单具有一些知识更重要得多,因此在传授学生一定数量知识的同时,还应教会学生一定的分析、判断、解题的能力。在数学分析教学中引导学生独立思考去求解数学分析问题,不仅帮助学生巩固知识点,而且挖掘了学生的创新潜能。在数学分析教学中不断地引导学生多思考,敢于设问和猜想、敢于另辟新径、敢于创新应用。