G-ρ不变凸多目标规划的鞍点条件

李向有

（延安大学数学与计算机科学学院，陕西延安 716000）

凸性理论在最优化理论、数学规划中具有很重要的地位，推广函数的凸性并用于研究数学规划问题是最优化理论的重要研究内容。G不变凸函数是近年来所提出的一类新的广义凸函数[1]，利用这类函数Antczak研究了可微多目标规划问题的最优性条件、对偶条件［2-3］，得到了许多重要结论。KANG等［4-5］在此基础上把G不变凸函数推广到非可微情形，研究了非可微G不变凸函数的最优性条件和对偶条件，得到了非可微情形下相应规划的最优性条件和对偶结果。近年来，ANTCZAK[6]把G不变凸函数推广到非可微向量情形，定义了非可微G-V不变凸函数，并用这类函数研究了多目标规划问题的最优性条件和对偶条件，推广了文献［2-3］的相关结论。李向有等[7]在此基础上，进一步定义了更广义的(G-V，ρ)不变凸函数，研究了多目标规划问题的Mond-Weir型对偶，刘婧雯等[8]研究了多目标规划的Wolfe型对偶。不完全Lagrange函数的鞍点问题，也叫混合鞍点问题，是更广义的一类鞍点问题，一般的鞍点问题可以看成是它的特殊情况，但相关研究文献却不多，文献［9-12］利用不同的广义凸函数研究了不完全向量值Lagrange函数的鞍点问题，得到了许多重要的结论。

本文在上述文献的基础上，定义了一类G-ρ不变凸函数、G-ρ不变拟凸函数、G-ρ不变伪凸函数，并用这类函数研究半无限多目标规划的鞍点问题，得到了不完全Lagrange函数鞍点的充分性条件和必要性条件。

1 基本定义

称实值函数f：Rn→R是局部Lipschitz的[13]，若对任意x∈Rn，存在一个正数k和x的邻域N(x)对任意y，z∈N(x)，使得

若函数f为局部Lipschitz的，那么函数f：X→R在点x处沿方向d的Clarke广义方向导数定义为［13］

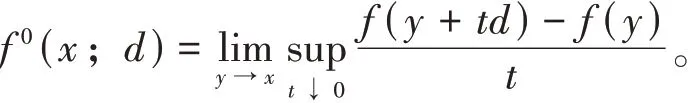
Clarke广义梯度定义为[13]

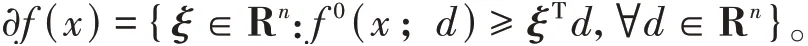
下面的不等式在整篇文章中都成立，对于任意x，y∈Rn，

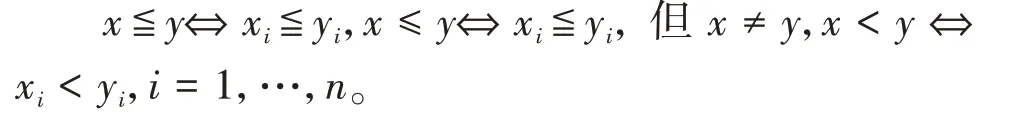
设X⊂Rn，u∈X，令f=(f1，…，f m)：X→Rn，f i(i=1，…m)是定义在X上的局部Lipschitz函数，令I f i(x)(i=1，…，m)表示f i的值。Antczak在文献［2-3］中定义了可微G不变凸函数，在文献［6］中定义了非可微(G，V)不变凸函数，受此启发本文定义非可微G-ρ不变凸函数类。

定义1令f=(f1，…，f m)：X→Rn，f i(i=1，…，m)是定义在X上的局部Lipschitz函数，函数G=(G1，…，G m)，G i：I f i(x)→R(i=1，…，m)是严格单调递增的可微实值函数，向量函数η：X×X→Rn，如果存在常数ρi∈R，函数d：X×X→R，使得对∀x∈X，∀ξi∈∂f i()，∈X，i=1，…，m，有

则称f在∈X是非可微G-ρ不变凸函数。若在上式中x≠且≧换成＞，则称函数f i在∈X是非可微严格G-ρ不变凸函数。

注1在定义1中，若ρi=0，则为文献［4-6］中所定义的非可微G不变凸函数；若ρi=0，ξi换成∇f(x)，则为文献［2-3］中所定义的可微G不变凸函数。所以本文所定义的函数是更广义的一类函数。

定义2令f=(f1，…，f m)：X→Rn，f i(i=1，…，m)是定义在X上的局部Lipschitz函数，函数G=(G1，…，G m)，G i：I f i(x)→R(i=1，…，m)是严格单调递增的可微实值函数，向量函数η：X×X→Rn，如果存在常数ρi∈R，函数d：X×X→R，使得对∀x∈X，∀ξi∈∂f i()，∈X，i=1，…，m，有

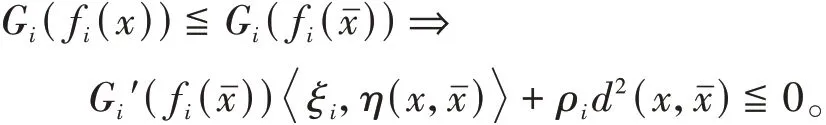
则称f在∈X是非可微G-ρ不变拟凸函数。

定义3令f=(f1，…，f m)：X→Rn，f i(i=1，…，m)是定义在X上的局部Lipschitz函数，函数G=(G1，…，G m)，G i：I f i(x)→R(i=1，…，m)是严格单调递增的可微实值函数，向量函数η：X×X→Rn，如果存在常数ρi∈R，函数d：X×X→R，使得对∀x∈X，∀ξi∈∂f i()，∈X，i=1，…，m，有

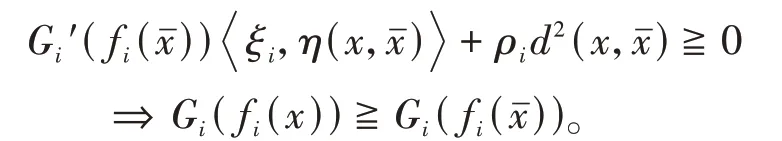
则称f在∈X是非可微G-ρ不变伪凸函数。

为了证明方便，先给出文献［12］中所定义的(V，ρ)不变伪凸函数。

定义4[12]令f=(f1，…，f m)：X→Rn，f i(i=1，…，m)是定义在X上的局部Lipschitz函数，向量函数η：X×X→Rn，如果存在常数ρ∈R，常向量λ∈Rn，λ≥0，函数d：X×X→R，使得∀x∈X，有

则称λΤf在∈X是非可微(V，ρ)不变伪凸函数。

下面给出一个非可微G-ρ不变凸函数和非可微G-ρ不变拟凸函数的例子。

例1令不难证明函数G i(f i(x))在xˉ=0处是非可微G-ρ不变凸函数。

例2令不难证明函数G i(f i(x))是非可微G-ρ不变拟凸函数。

2 鞍点条件

考虑下列半无限多目标规划（VP）

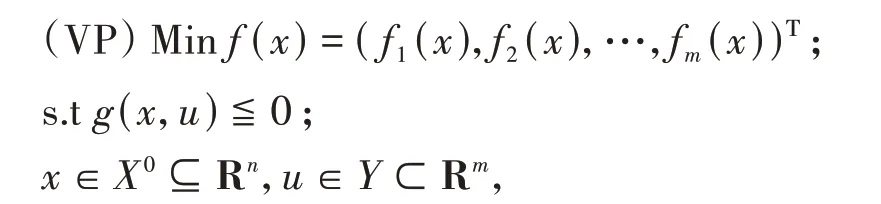
称L(x，v j)=(L1(x，v j)，L2(x，v j)，…，L m(x，v j))Τ为（VP）的G不完全Lagrange函数。这里

上式中，若m=1，J2=ø，约束函数个数为有限个，则G不完全Lagrange函数即为文献［14］所定义的G-Lagrange函数；若G i(a)=a，约束函数个数为有限个，则G不完全Lagrange函数即为文献［12］所定义的混合Lagrange函数。

定义5 点()∈X×Λ1称为不完全向量值Lagrange函数的G鞍点，若它满足下面条件：

定义6设是（VP）的可行解，如果存在严格单调递增的实值可微函数G i，，i=1，…，m，j∈Δ，(i=1，…，m)，(j∈Δ)，对于∀uj∈Y有

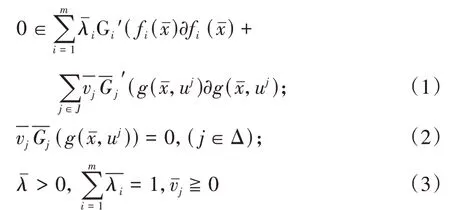
成立，则称为规划（VP）的G-(K-T)点。

引理1[13]对于任意实数s i和实函数f i总有成立，如果至少有一个f i在x严格可微，则有

定理1设(x，)在处是非可微(V，ρ)不变伪凸函数，g(x，uj)，j∈J2在xˉ处为非可微-不变拟凸函数，并且至少有一个f i(i=1，…，m)和至少 有 一 个g(x，u j)，j∈J1在严 格 可 微；为 规 划（VP）的G-(K-T)点则存在∈Λ1，使得为不完全向量值Lagrange函数的G鞍点。

证明因为xˉ为规划（VP）的G-(K-T)点，由（1）式可得，

通过多样性指数分析发现：在T0、T1和T2期曲块中，真核微生物多样性较高；在T3、T4和T5期，多样性较低。4种计算方法的结论基本一致（表4）。该数据亦表明，真核微生物在制曲过程中，在外界（如温度）条件影响下，真核微生物的多样性呈下降趋势。

又≧0，g(x，u j)≦0，是严格单调递增的可微实值函数，故有((g(x，u j)≦0，结合（2）式，有

由条件g(x，u j)，j∈J2在xˉ处为非可微不变拟凸函数，可得∀σj∈∂g(，uj)，j∈J2，有

即有

再由(x，v j)在xˉ处为非可微(V，ρ)不变伪凸函数，可得

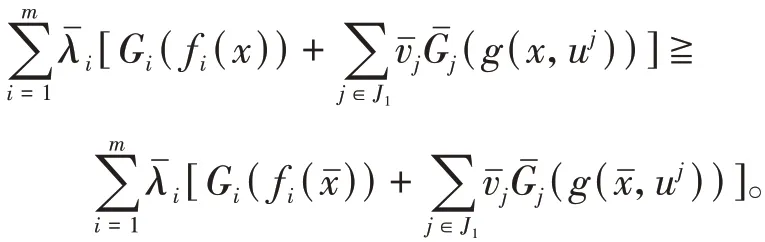
对于∀v j≧0，x∈X，g(x，uj)≦0，是严格单调递增的可微实值函数，故有v j(g(x，u j))≦0，结合（2）式，有

定理2设f(x)在处为非可微G-ρi不变凸函数，g(x，uj)，j∈J1在处为非可微-不变凸函数，g(x，uj)，j∈J2在处为非可微-不变拟凸函数为规划（VP）的G-(K-T)点，

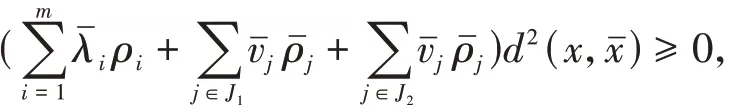
证明因为为规划（VP）的G-(K-T)点，由（1）式可得，

f(x)在为非可微G-ρi不变凸函数，故∀ξi∈∂f i()，σj∈∂g(，uj)，i=1，…，m，j∈J1，有

用(i=1，…，m)乘以上式两端，并把各式相加可得

g(x，uj)，j∈J1在处为非可微-不变凸函数，可得∀σj∈∂g(，uj)，j∈J1，有

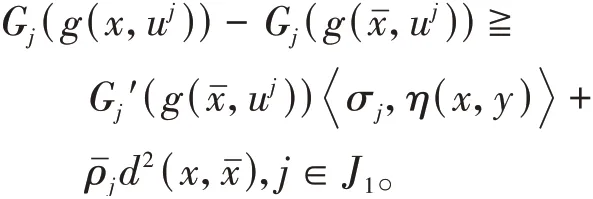
用，j∈J1乘以上式两端，并把各式相加可得

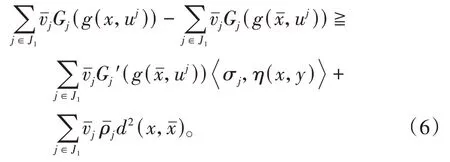
由条件g(x，u j)，j∈J2在xˉ处为非可微-不变凸函数，可得，有

即有

结 合（4）式、（5）式、（6）式、（7）式 和 条 件可得

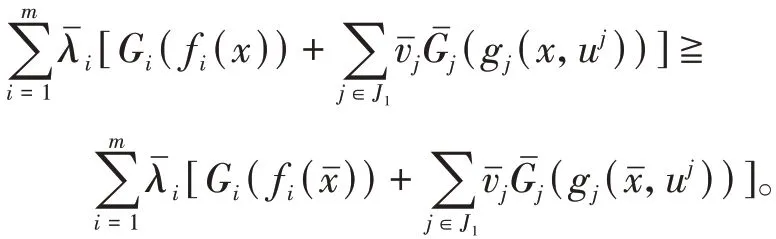
再由定理1的证明类似可得

定理3 令是不完全向量值Lagrange函数的G鞍点，则是（VP）的有效解。

证明因为是不完全向量值Lagrange函数的鞍点，则有，即

即有

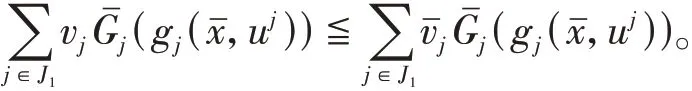
由于v j的任意性，当时，

假设xˉ不是（VP）的有效解，则存在（VP）的可行解x0有f(x0)≤f()，即f i(x0)≦f i()，i=1，…，m，且至 少 有 一 个k，使 得f k(x0)＜f k()，由 于G i，i=1，…，p是严格单调递增的可微实值函数，所以有G i(f i(x0))≦G i(f i())，i=1，…，m，且至少有一个k，使得G k(f k(x0))＜G k(f k())。又因为x0是（VP）的可行解，故有

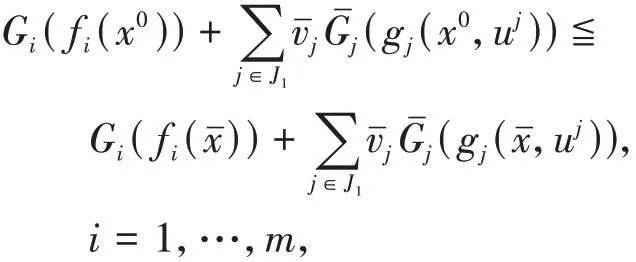
且至少有一个k，使得