基于AFSA-PSO-LSSVM的风电机组齿轮箱故障诊断

王一宁，甄成刚，韩瑶瑶

(华北电力大学 控制与计算机工程学院 河北 保定 071003)

0 引言

风电机组通常安置于环境恶劣、偏僻及风能资源丰富的地区，根据风能资源的分布情况，为了更好地捕捉风能，机舱安装高度越来越高，从而造成检查维护不便[1]。齿轮箱作为风电机组中重要的机械部件，是极易发生故障的，故障停机带来的经济损失也是不可避免的，因此对风机齿轮箱进行故障诊断具有重要的经济意义[2]。

混合智能算法最小二乘支持向量机(least squares support vector machine，LSSVM)是目前研究的一个热点。不少国内外学者对相关算法进行了很多优化研究，如粒子群算法(particle swarm optimization，PSO)、遗传算法(genetic algorithm，GA)等[3]。

文献[4]提出了基于PSO优化LSSVM模型参数的方法，通过结合集合经验模态分解与样本熵作为特征信号，最终构建的PSO-LSSVM模型不仅能够提高熵计算中的相似容限值、避免了参数选取的盲目性，还明显提高了风电机组齿轮箱故障识别率。文献[5]使用鲸鱼算法(whale optimization algorithm，WOA)优化LSSVM模型的两个参数，利用鲸鱼算法运算速度快、全局寻优能力强的优点帮助LSSVM算法跳出局部极值，采用了一种基于改进集合经验模态分解(modified ensemble empirical mode decomposition，MEEMD)的方法分解齿轮箱振动信号数据，搭建了WOA-LSSVM风电齿轮箱故障诊断模型，并验证了该模型的有效性和优势。但鲸鱼算法依然存在收敛慢、寻优精度低等问题，对此，文献[6]提出了一种改进的鲸鱼算法，优化LSSVM算法参数，利用互补总体经验模式分解能量熵提取特征，并降低了故障信号的干扰，使用VN拓扑结构优化了鲸鱼算法的搜索能力。搭建的VNWOA-LSSVM分类模型相较于WOA-LSSVM模型，明显提高了分类正确率。文献[7-8]虽采用LSSVM等相关算法对故障特征的提取做了一定的研究，但并未对LSSVM算法参数进行相关优化。文献[9-12]均采用相关算法优化LSSVM参数，并对电力设备作相应的故障识别，其结果均能有效判别故障类别。

文章针对LSSVM算法参数的盲目选取，不易跳出局部极值，人工鱼群算法(artificial fish swarm algorithm，AFSA)后期收敛不足及PSO算法局部收敛较差和精度小等问题，提出了一种基于AFSA和PSO混合智能算法，优化LSSVM模型参数，结合风电机组齿轮箱的振动信号数据，搭建了基于AFSA-PSO-LSSVM混合智能算法的风电机组齿轮箱故障诊断模型。

1 LSSVM

支持向量机[13](support vector machine，SVM)是一种基于统计学理论的机器学习算法。虽然具有较强的泛化能力，但其不等式函数求解比较复杂，文献[14]提出了一种改进的LSSVM算法，为了将不等式约束变为等式约束，将最小二乘线性系统用作损失函数。

设训练样本为N{(x1,y1),(x2,y2)，…,(xi,yi)}，其中：x、y分别为训练样本的n维输入和输出。设LSSVM目标优化函数为

(1)

其中：ζ为可控参数；w为权重向量；C为正规化参数，用于拟合误差；ei为误差，需要满足

yi=wTφ(xi)+b+ei，i=1,2,…,N，

(2)

其中：φ(x)为映射函数；b为偏执值。

拉格朗日函数为

(3)

其中：αi为拉格朗日乘子，求导可得

(4)

通过转换为求解线性方程，消除ω和e得

(5)

其中：IN为N维单位矩阵；1m=[1,1,…,1]，共m个1。

Ωij=φ(xi)Tφ(xj)=K(xi,xj)，

(6)

最终得到LSSVM模型的决策函数y(x)为

(7)

取径向基函数K(xi,xj)为

K(xi,xj)=exp(-‖xi-xj‖2/σ2)，

(8)

其中：σ为核函数带宽。

2 混合智能算法设计

2.1 PSO

粒子群优化(particle swarm optimization，PSO)算法是由Kennedy G 和 Eberhart R在1995年受到鸟群或鱼群活动规律启发所提出的一种基于群体智能的演化算法[15]。PSO算法与很多先进的算法(如遗传算法)有相同之处，但相比于遗传算法，并没有交叉和变异等操作，PSO算法也是随机得到潜在解，然后通过更新后代，实现搜索寻优。在PSO算法中，粒子X(i)是由d维实数向量表示的候选解，k为第k个维度上的参数[16]。X(i,j)表示第i次迭代时，第j个粒子的位置，

Xj(i)=[xj,1(i);xj,2(i);…;xj,k(i);…;xj,d(i)]，

(9)

其中：x是带寻优参数；xj,k(i)是第j个候选解中第k个待寻优参数；d是控制变量的总数。每个控制变量的取值范围为[xmin,xmax]，此时种群可以表示为

pop(i)=[X1(i),X2(i),…,Xn(i)]T，

(10)

其中：n为种群中粒子的个数。使用目标函数评估种群中的所有粒子，若候选解为可行解，则更新迭代次数i=i+1，否则继续重复此步骤。在第i次迭代中，粒子的速度V(i)可以表示为

Vj(i)=[vj,1(i);vj,2(i);…;vj,k(i);…;vj,d(i)]，

(11)

其中：vj,k(i)是第j个粒子第k维上的速度分量。速度更新时，将按照全局最优和个体最优来进行指导更新，更新公式为

(12)

其中：ω为权重；C1、C2为加速因子；rand为[0,1]内的均匀随机数。然后开始检查粒子速度情况，将速度控制在合适的范围内。粒子将根据已更新的速度，更新自己的位置，

x(k,j,i+1)=x(k,j-1,i)+v(k,j,i)。

(13)

在粒子的搜索飞行过程中，不断地将当前位置与最佳位置进行比较，更新个体最优。最后，将得到的所有个体的最优位置相比较，得到群体的最佳位置，满足设定条件则终止搜索。

2.2 AFSA

人工鱼群算法是一种仿生智能算法，通过模拟鱼群在游动过程中出现的觅食、聚群、追尾及随机行为[17]，并通过不断调整算法的参数，在给定的范围中寻求出最优解。每一条人工鱼(artificial fish，AF)都封装了其自身数据信息(如视野范围、移动步长等)和一系列日常交互行为(觅食行为、聚群行为等)，并接收环境信息来做出相应活动。人工鱼群算法实现过程如下。

1)初始化鱼群。设鱼群规模为M，初始化鱼群(AF)个体向量为Xi={a1,a2,…,an}，其中ai为寻优变量，根据实验初始化鱼群M和AF个体，Xa为AF个体的状态，并设AF下一状态为Xa|next|。

2)觅食行为。设鱼群个体视野范围内的选择随机状态及其所在位置食物浓度分别为Xb和Ab。当Xb>Ab时，则循着这个方向前进，否则选择另一个随机方面Xb。如果尝试到一定的次数后，还不能前进则执行随机。

3)追尾行为。设Xb为人工鱼伙伴，m为人工鱼视野范围内伙伴总数，拥挤度因子δ凸显全局最优，搜索伙伴所在位置食物浓度最高的一个。若Ab/m>δAa，则可以与伙伴Xb共生，向Xb方向前进，否则进行觅食。

4)聚群行为。设某条人工鱼的伙伴中心位置为Xcenter，若Xcenter/m>δAa，则证明伙伴中心位置食物浓度高，可以与该伙伴共生生存，并向着此方向前进，否则进行觅食。

5)随机行为。当某条人工鱼多次觅食行为仍然不能前进，则进行随机行为，选择视野内一个随机状态前进一步。

觅食、追尾、聚群、随机这些基本行为通过表征参数变化、随机搜索及聚群追尾等行为向全局最优值收敛。人工鱼群算法寻优速度快、全局搜索能力及适应性强等优点，为求解最优问题提供了灵活的架构。相对于BP神经网络等单一收敛方式的传统智能算法，人工鱼群算法的全局适应性更佳[18]。

为了弥补LSSVM算法参数盲目选取的缺陷，设计了人工鱼群算法和粒子群算法相结合的混合智能优化算法，并搭建了基于该混合智能算法的风电机组齿轮箱故障诊断模型，使用该模型即可判别出齿轮箱的正常、磨损及断齿的实际状态。

2.3 AFSA-PSO-LSSVM

混合人工鱼群和粒子群算法的思想是：利用人工鱼群算法开始全局寻优，确定好LSSVM算法参数的初值，再利用粒子群算法进行局部搜索并更新上一步的解，加快算法跳出局部最优，从而避免了早期缺乏信息素产生收敛过慢的问题[19]，随着后期搜索方向的确定，从而加快了全局最优解的获得。然而PSO算法迭代速度快、结构简单，因此可以对AFSA算法和PSO算法进行取长补短，结合AFSA算法的全局寻优能力、适应能力和PSO算法结构简单、运算快的等优点，不仅解决了LSSVM算法参数盲目选择及不易跳出最优解的问题，还解决了AFSA后期收敛不足和PSO容易陷入局部最优等缺点。而AFSA-PSO-LSSVM算法融合了两个算法各自优点，在寻优和收敛速度上具有一定的优势。人工鱼群与粒子群混合智能优化算法步骤如下。

1)初始化人工鱼群规模、每条人工鱼状态、视野范围、移动步长、拥挤度因子、最大重复尝试次数、粒子群的加速因子、人工鱼个数、粒子群个数等。

2)根据食物浓度计算每一条人工鱼的适应度。

3)进行每条人工鱼的行为选择，通过觅食、追尾、聚群和随机行为更新自己的位置。

4)判断人工鱼群终止条件。如果满足了迭代条件则将得到的初值赋值算法模型，否则进行下一次迭代，继续进行鱼群相应的行为选择。

5)初始化每个粒子的位置和速度，将人工鱼群满足迭代条件的信息值传递给粒子群。

6)使用目标函数评估种群中的所有粒子适应度。

7)检查每个粒子速度，并将速度控制在合适的范围内，根据自身速度更新位置。

8)搜索飞行，比较每个粒子自身位置与历史最佳位置，当前位置较优则设为当前最佳位置。

9)将所有粒子的最优位置进行比较，得到全局最佳位置。

10)检查迭代条件，如果满足预先设定的终止条件，则终止迭代，算法完成，否则继续搜索飞行。

3 齿轮箱故障诊断模型搭建流程

AFSA-PSO-LSSVM算法模型对风电机组齿轮箱故障进行智能识别诊断的步骤如下：首先从齿轮箱振动信号中进行特征提取，提取有关故障信息后将数据进行归一化处理，输入到混合智能算法中进行训练，通过训练数据集得出模型，并用测试集数据输入到AFSA-PSO-LSSVM模型中进行测试对比。

在该诊断流程中，通过传感器采集到的齿轮箱振动信号数据预处理后，即小波降噪、时频域转换等计算出所需的特征参数，归一化后输入到训练好的AFSA-PSO-LSSVM混合智能算法模型中，并将测试数据输入到该模型，所得到的归一化结果即可诊断齿轮正常、磨损及断齿等状态。

4 模拟实验

齿轮箱部件是否正常运行，对于风电机组转动系统是至关重要的，直接影响到整个风机的工作。齿轮箱常年工作在酷暑、严寒等极端自然环境下，在高速、重载下运行的齿轮，其工作条件又相比其他零件恶劣。

4.1 数据选择与数据处理

为了模拟AFSA-PSO-LSSVM算法模型下的故障诊断效果，选取了某风电场1.5 MW风电机组齿轮箱的振动加速度信号数据，采样频率为5 120 Hz，采样样本数为8 192点，机组容量为750 kW，年平均风速为7.6 m/s，已运行7年。由于时域波形所包含的信息量大，并不容易将信息中心的故障信息提取出来并定位故障类型和故障部位。因此采用了目前效果较好的小波变换时频分析技术进行降噪，并将时域数据变换到频域数据图谱上[20]，例如当磨损到了一定的程度，齿啮合的频率的幅值会明显变大，磨损后的频域功率谱波形中出现了翻倍的啮合频率。

在齿轮箱的故障占比中，齿轮故障比重约占60%，所以选取了齿轮故障中的齿轮断齿、齿面磨损2种故障类型。齿轮无论是在正常或是在异常状态下，齿轮之间的啮合都会产生振动。外加齿轮负载的不平衡，齿距不均匀等因素造成齿轮箱振动加速度信号的复杂性和不平稳性。故选取了时域分析、频域分析和时频域分析的敏感故障特征参数：功率谱熵、峭度、偏度、关联维数、盒维数和小波熵等指标作为齿轮箱故障诊断模型的特征向量。

处理后共135组特征数据，分别将试验训练样本和测试样本以2∶1的比例进行切分。

4.2 实验参数设定

LSSVM算法参数的设定：惩罚因子C的变化范围为[0.1,100]；核函数σ变化范围为[0.01,10]。

PSO算法参数的设定：最大训练次数为50；训练精度为0.01；学习速率为0.1；最大飞行速度为1；最小飞行速度为-1；种群粒子个数为20；学习因子C1、C2均为1.494 45；最大迭代次数为100。

AFSA算法参数设定：实验采用人工鱼群中总人工鱼数为20条；最大迭代次数为50；最多试探次数为5次；拥挤度因子为0.618；最大步长为0.05；感知距离为0.2。

设定Rastrigin优化函数：分别对三种算法模型进行优化测试。所取函数为

(14)

其中：xi在-5到5之间。

设定误差评价指标：相对误差和平均绝对误差函数为

(15)

(16)

其中：yi为实际值；yLi为输出预测值；EMAE为相对误差；EMAPE为平均绝对误差。

4.3 实验结果分析

实验数据分为两部分：训练数据90组，测试数据45组。在Matlab仿真环境下，对90组输入和输出样本进行训练并进行建模，将风电机组齿轮箱实验数据去噪、特征提取后，归一化输入到PSO-LSSVM、AFSA-LSSVM及AFSA-PSO-LSSVM三个模型中。在Rastrigin优化函数优化测试下，分别得到了3个算法模型的适应度函数曲线。三种混合智能算法的适应度函数曲线及相对误差曲线分别如图1和图2所示。

由图1可知，3个算法模型分别经历了58次、48次、39次完成了最终迭代。PSO-LSSVM算法前期计算快，但在粒子俯冲过程中可能会错失全局最优解，后期容易陷入局部极值点。AFSA-LSSVM算法因其全局搜索能力较强的优势，历经11次迭代后适应度函数值从51迅速减小到27。PSO-LSSVM算法需要经历23次迭代，然而随着迭代次数的增加，后期收敛不足，收敛速度慢，仍有可能陷入局部极值点。而AFSA-PSO-LSSVM不仅解决了收敛速度慢的问题，还解决了陷入局部最优解、时间过长等问题，达到了相互进化、取长补短的目的。AFSA-PSO-LSSVM算法最终历经了39次迭代，函数值最终稳定在0。由此可知，相较于PSO-LSSVM算法和AFSA-LSSVM算法，AFSA-PSO-LSSVM算法在寻优和收敛速度上具有一定的优势。

图1 适应度函数曲线Figure 1 Fitness function curve

从图2的3种模型相对误差变化可以看出，PSO-LSSVM、AFSA-LSSVM及AFSA-PSO-LSSVM的最大相对误差分别为6.88%、5.62%、3.64%。此外3种算法模型的平均绝对误差分别为5.16%、3.87%和2.07%，不难看出，AFSA-PSO-LSSVM算法模型的相对误差最小，平均绝对误差也最小，模型效果最佳。

图2 相对误差曲线Figure 2 Relative error curve

为更好地观察实验结果，分别将45组测试数据输入到PSO-LSSVM、AFSA-LSSVM和AFSA-PSO-BP实验组进行识别，纵坐标编号1～3分别为齿轮箱的3种状态：正常、磨损和断齿，编号4为模糊识别结果，横坐标为实验组编号。识别结果如图3～5所示。

图3 PSO-LSSVM实验组诊断结果Figure 3 PSO-LSSVM experimental group diagnosis results

图4 AFSA-LSSVM实验组诊断结果Figure 4 AFSA-LSSVM experimental group diagnosis results

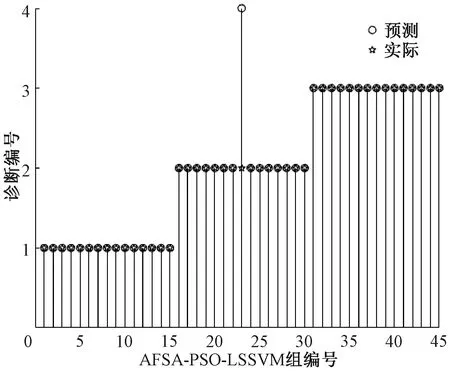
图5 AFSA-PSO-LSSVM实验组诊断结果Figure 5 AFSA-PSO-LSSVM experimental group diagnosis results

由图3可知，PSO-LSSVM实验组中的第22组和第36组样本发生了诊断错误，第7组样本为模糊诊断，共计42组样本诊断正确，正确诊断率为93.33%。由图4可知，AFSA-LSSVM实验组中的第28组发生错误诊断，第19组为模糊诊断，正确诊断组数为43组，正确诊断率为95.56%。相较于PSO-LSSVM提升了2.23%。由图5可知，AFSA-PSO-LSSVM实验组中的第23组发生了模糊诊断，正确诊断组数为44组，正确诊断率为97.78%，相较于PSO-LSSVM和AFSA-LSSVM分别高了4.45%和2.22%。

最后，分别对三个齿轮箱故障诊断模型进行了50次测试，综合统计结果如表1所示，明显可知AFSA-PSO-LSSVM算法模型的齿轮箱故障诊断效果优于PSO-LSSVM和AFSA-LSSVM算法模型。同时也可以看出，AFSA-PSO-LSSVM混合智能算法的误差平均值为0.769 8，低于PSO-LSSVM算法以及AFSA-LSSVM算法。由此说明，此混合智能算法模型诊断误差较小，精度高，应用于风电机组齿轮箱的故障诊断是可行的。

表1 齿轮箱故障诊断结果Table 1 Fault diagnosis results of gearbox

5 结语

本文提出一个人工鱼群和粒子群混合智能算法优化LSSVM参数的方法，通过鱼群算法进行全局寻优，再利用粒子群算法局部更新求解，解决了LSSVM算法盲目选取参数的问题。搭建了AFSA-PSO-LSSVM混合智能算法模型，对风电机组齿轮箱进行故障诊断。通过实验对比，AFSA-PSO-LSSVM混合智能算法的诊断模型收敛速度更快，诊断精度和性能都得到了进一步的提高，验证了AFSA-PSO-LSSVM混合智能算法模型的有效性和可行性，为风电机组齿轮箱的故障诊断提供了一个新的解决方法。