一种求解旅行商问题的信息传播算法
程亚南,王晓峰,2,刘凇佐,刘子琳
(1.北方民族大学 计算机科学与工程学院 宁夏 银川 750021;2.北方民族大学 图像图形智能处理国家民委重点实验室 宁夏 银川 750021)
0 引言
旅行商问题(traveling salesman problem,TSP)[1]早在1959年提出,是著名的NP难问题。TSP的本质是在给定约束条件下,使得问题的目标函数取得最小值。TSP应用广泛,是组合优化问题的典型代表,在运筹学中占据重要地位,如物流配送问题[2]、车辆路径规划问题[3]等。在问题提出的早期,研究人员利用分支限界法和回溯法等一些确定性算法对该问题进行求解,但是随着问题规模的增加,求解难度增大,计算时间呈现指数级增长。因此,启发式的群智能优化算法被用于求解TSP,如遗传算法(genetic algorithm,GA)[4]和粒子群算法(particle swarm optimization,PSO)[5]等。这些群智能优化算法对于求解大规模的TSP有一定的优势,但在求解质量上存在精度不高等缺点。研究人员通过对这些经典算法进行改进或者与其他智能优化算法融合,不断提高算法的性能[6-7]。
置信传播(belief propagation,BP)算法是信息传播算法[8]的一种,以和-积[9]的形式进行信息传递。BP算法的特征是基于因子图上的边传递消息,当这种消息传递达到一种稳态时,可计算因子图上节点取值的边际概率,从而以高概率确定变元的某种取值,BP算法可以很好地求解组合优化问题。本文将非负权重图G(V,E)转化为因子图模型,将TSP中城市之间的边映射为因子图模型中的变量节点,将城市和约束条件节点映射为因子图模型中的因子节点,利用线性规划方程构造BP算法的势函数,进而提出一种求解TSP的BP算法,当该算法达到一定迭代次数时,以高概率确定TSP的初始解,调用局部搜索算法进行计算,获取TSP的最优解。实验结果表明,该方法求解速度较快且解的精度较高。
1 基本知识
1.1 因子图
因子图[10]是一个特殊的二分图,可以直观地表现一个多种约束条件的复杂问题。因子图将一个具有多个变量的全局函数分解为几个局部函数的乘积,这里的乘积是广义乘积,可以表示不同的对应关系。如G(x1,x2,x3)是具有三个变量的全局函数,将该函数进行分解得到四个局部函数f1、f2、f3、f4,可以表示为
G(x1,x2,x3)=f1(x1,x3)f2(x1)f3(x1,x2)f4(x2,x3)。
(1)
因子图中包含两种节点:圆形的变量节点和正方形的因子节点。两种节点之间通过无向边进行连接,变量节点表示联合概率分布函数的自变量,因子节点是分解后的局部函数。构造对应关系为式(1)的因子图,因子图示例如图1所示。
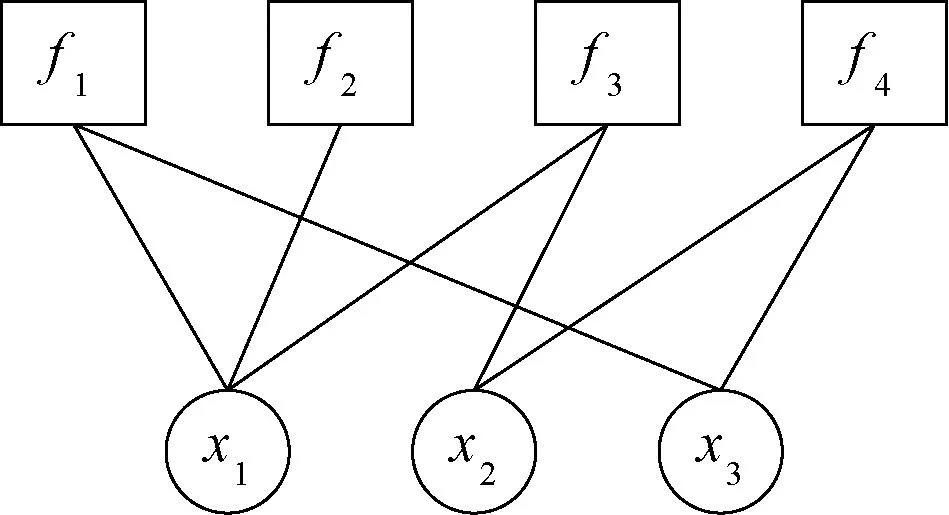
图1 因子图示例Figure 1 Example of factor graph
1.2 最小和信息传播算法
信息传播算法是基于因子图上的边进行消息迭代的算法,因此因子图是运用信息传播算法求解问题的关键。对于信息传播算法而言,主要存在和积算法和由和积算法简化的最小和算法[11]。
最小和信息传播算法[12]是一个信息逐步迭代的过程,在因子图的边(i,α)上,信息随着过程的迭代进行更新。μi→α(di)表示由变量节点发给因子节点的信息,代表变量i取值为di的信息;μα→i(di)表示由因子节点发给变量节点的信息。信息迭代方程为
(2)
(3)
式中:V(i)代表与i相连接的因子节点集合,V(i)α表示不包含α的因子节点集合;V(α)表示与α相连接的变量节点集合,V(α)i表示不包含i的变量节点集合;fα(dj)是对应问题的描述函数,也称为势函数。当BP算法收敛时,边际信念表示为
(4)
该算法的伪代码描述如下。
算法1最小和信息传播算法
输入:因子图,最大迭代次数tmax,精度ε。


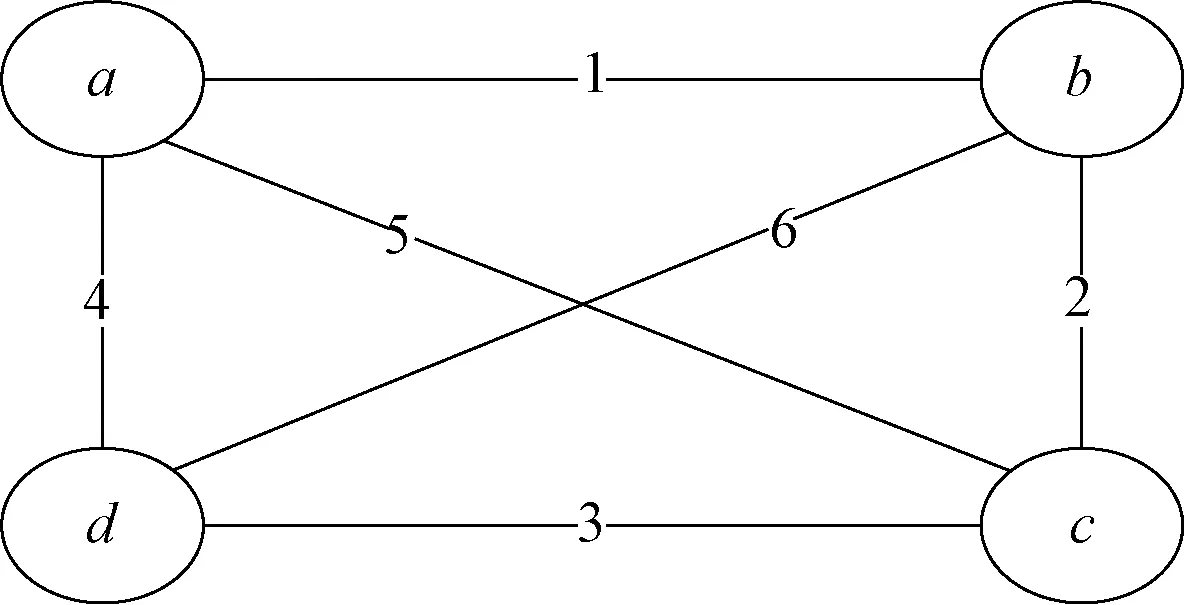
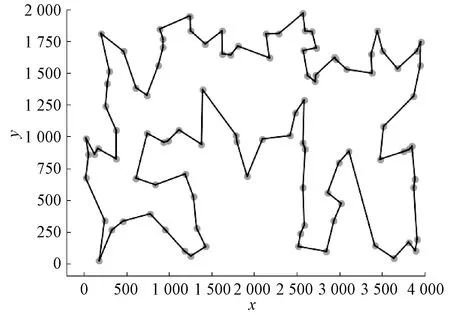
1 Whilet 2 对于每一个变量i利用式(4)计算φi(di); 在给定的非负权重无向图G(V,E)中,考虑到TSP要求一个城市有且仅有两条边相连的约束条件,TSP的线性规划方程为 minimize:wTx, x=[xe]∈[0,1]|E|, (5) 其中:w=(w1,w2,…,wm)代表图中各边的权重(距离);x=(x1,x2,…,xm)T是定义边的标签属性,如果标签x1值为1,则将该边加入回路,反之则不加入回路;∂(v)是顶点v所连接的边;xe是顶点v加入回路边的数量;|E|是边数目的模。 G(V,E)表示一个无向图,wi:j为i和j两个节点之间的非负距离,其中节点集合V={v1,v2,…,vn},(i:j)=1表示顶点vi和顶点vj之间存在边。令d={d1,d2,…,dM}∈{0,1}M是一组M维二进制变量,其中M=|E|。di:j=1代表节点i和节点j所在的边在TSP的可行解中。 根据TSP的特性,定义以下两种约束条件。 1)成本约束:代表因子图上边的成本,当i和j两个节点存在边,信息为非负距离,反之为0。 (6) 2)势函数:确保每个节点刚好都与其他两个节点连接。 (7) 图2是包含四个城市的简单无向图示例,其中a、b、c、d代表四个城市,边上的数字代表城市之间的权重。四个城市的因子图示例如图3所示,在因子图的转换过程中,将城市之间的边作为变量节点,城市和约束条件(势函数)作为因子节点,其中白框代表城市,黑框代表约束条件。 图2 四个城市的无向图示例Figure 2 Example of undirected graph for four cities 图3 四个城市的因子图示例Figure 3 Example of factor graph for four cities 文献[13]针对消息传递的复杂性,提出简化信息的方法。根据TSP的特性,当di:j=1时,表示节点i和节点j的边选入路径,反之则不选入。令min[k]A表示集合A中第k个最小值,将式(3)进行重写,可得消息的更新公式为 (8) 考虑到BP算法在求解过程中会产生消息震荡,影响收敛速度,同时为了进一步提高BP算法信息更新的收敛速度,使用特定的阻尼策略来减轻消息振荡[14],将消息更新为最近两次迭代信息的平均值, (9) 模拟退火的思想是在搜索过程中进行随机搜索,在迭代过程中以一定的概率值接受当前较差的解,防止求解过程中陷入局部最优。高温时,粒子处于无序状态,较差解容易被接受;低温时,粒子状态逐渐稳定,算法收敛。在TSP中,模拟退火算法对路径的优化过程如下:① 对初始温度、退火系数、迭代次数、最终温度等进行初始化,假定初始解为R,计算适应度值f(R)。② 在降温的过程中,扰动产生新的路径R1,计算适应度值f(R1)。③ 比较两次路径的适应度值之差,若f(R1)≤f(R),则R=R1;否则,按照Metropolis准则进行更新。④ 判断是否达到终止条件。 模拟退火算法能有效防止算法陷入局部最优解,具有良好的全局搜索能力,用于求解TSP效果显著。 局部搜索(local search,LS)使用交换、逆序、插入三种操作,利用轮盘赌算法的方式来选择增加邻域结构,以退火的思想接受较差的解,防止陷入局部最优。例如,当前城市路径为1→3→4→6→2→7→8,局部搜索的三种操作如下。 1)交换操作。随机选取两个城市进行交换来修改路径,如果选择的城市是3和7,那么变换后的城市序列为1→7→4→6→2→3→8。 2)逆序操作。随机选取两个城市,将以两个城市为首尾的城市逆序。如果选择的城市是3和7,那么进行逆序操作后的序列为1→7→2→6→4→3→8。 3)插入操作。随机选取两个城市,选择进行插入操作的为i=3和j=7。如果i 将信息传播算法处理后的结果中加入局部搜索进行求解,对得到的初始结果进行优化。算法具体步骤如下。 算法2求解旅行商问题的信息传播算法 输入:图G=(V,E),最大迭代Tmax,阈值εmax。 输出:巡视中路径Tour⊂E。 1 构造初始化因子图; 4 While True 4.1ε←0,T←0; 4.2 Whileε<εmaxandT 4.2.1 For eachI=f∂vi∥从该因素更新所有传出的消息; 4.2.1.2 For eachi:j∈I; 4.2.1.7T←T+1; 4.4Tour加入解列表Tours; 4.5 If |Tours|==50; 4.5.1 BestTour←LS(Tours),break 4.6 Else 4.6.1 在Tour中随机选取一条边,在G(E,V)中删除选中的边; 4.6.2 生成新的G*(V,E′),传入新G*(V,E′),转到步骤1。 为了检测本文算法的性能,使用TSPLIB中标准数据集作为实验数据进行测试。实验环境为:Python3.7,Inter(R)i7-9750H 2.60 GHz,内存为8 GB。局部搜索过程中交换概率设为0.2,逆序概率设为0.5,插入概率设为0.3,BP算法产生的初始解数量设置为50。 选择随机初始解(RD)算法、贪婪策略初始解(GR)算法与BP算法进行初始化对最终解影响效果的对比实验。选取小型数据集Chn31、Att48、Berlin52和大型数据集KroA100,不同数据集的最终解结果如表1所示。图4为不同初始化算法在Chn31数据集上的迭代过程,图5对比了GR和BP算法在KroA100数据集的迭代过程。 表1 不同数据集的最终解结果Table 1 Final solution results of different data sets 图4 不同初始化算法在Chn31数据集上的迭代过程Figure 4 Iterative process of different initialization algorithms on Chn31 data set 图5 GR和BP算法在KroA100数据集的迭代过程Figure 5 Iterative process of GR and BP algorithms on KroA100 data set 由表1、图4和图5可知,在Chn31数据集上采用RD和GR算法初始化,在20次迭代中未达到最优解,而BP算法初始化在第5次迭代就得到最优解。在Att48、Berlin52和KroA100数据集上采用RD和GR算法初始化,迭代结果较差。而BP算法初始化在Att48、Berlin52数据集上达到已知最优解,在KroA100数据集上接近最优解。随着城市的增加,初始化对计算效率和解的精度的影响会越大。 选取经典的粒子群算法(PSO)、遗传算法(GA)与BP算法进行同等时长(60 s)的对比实验,运行状态情况如表2所示。因为PSO和GA在运行时随机初始化会影响运行的时间和解的精度,所以在求解前使用GR提高效率。三种算法在Chn31和Att48数据集上的运行结果对比分别如图6和图7所示。 表2 同等时长的运行状态Table 2 Running status of the same duration 图6 不同算法在Chn31数据集上的运行结果对比Figure 6 Comparison of running results on Chn31 data set by different algorithms 图7 不同算法在Att48数据集上的运行结果对比Figure 7 Comparison of running results on Att48 data set by different algorithms 由图6可知,在Chn31数据集上,三种对比算法在初始时差别不大,随着运行时间的增加,PSO收敛变慢,收敛的结果较差,GA比PSO和BP算法收敛快,但是没有跳出局部最优的能力,求解效果不如BP算法。由图7可知,在Att48数据集上,同在60 s的时间里,相对于PSO和GA而言,BP算法在最初时结果就更好;PSO和BP算法收敛的时间相近,但是BP算法的效果要好得多,而GA虽然早早地收敛,但是与结果相差太大,明显是陷入局部最优解。 选取8种不同规模的TSP实例,运用本文算法进行20次独立运行实验,局部搜索迭代次数为500,大型数据集KroA100和Ch130的迭代次数设置为1 000。为了验证本文算法的性能,与改进的启发式算法进行对比,分别比较了文献[15]提出的自适应模拟退火蚁群算法SA-MMAS和文献[16]提出的多策略改进蚁群算法MSIACA;与新型启发式算法进行对比,分别比较了文献[17]提出的离散狼群算法DWPA、文献[18]提出的离散蝙蝠算法DBA和文献[19]提出的变邻域量子蝙蝠算法VNQBA。TSP实例测试结果如表3所示,表中数据集名称后的数字即为城市规模大小。 由表3可以看出,本文算法在计算100个城市以内的实例中都可以找到最优解,平均解优于其他算法;在实例Ch130中找到的最优解和平均解优于VNQBA算法,但是效果低于MSIACA算法。本文算法对于TSP有较高的求解质量,BP算法初始化提高了初始解的质量。因此,将信息传播算法应用于求解TSP,在标准数据集的测试结果对比中,迭代次数少于对比算法的同时求解质量优于对比算法。针对不同的数据集,本文算法可以求得标准最优解。图8和图9分别是St70和KroA100数据集的最优路径图。 图8 St70数据集的最优路径图Figure 8 Optimal path diagram of St70 data set 表3 TSP实例测试结果Table 3 TSP instance test results 图9 KroA100数据集的最优路径图Figure 9 Optimal path diagram of KroA100 data set 本文提出一种新的求解TSP的信息传播算法,利用因子图的特性和BP算法的传播性,随机选择开始城市,在因子图上进行迭代运算。结果表明,在城市数目较少的情况下,信息传播算法可以在较少的迭代次数中直接求得最优解。但是随着城市数目的增加,因子图会变得复杂,从而影响解决问题的效率,而加入局部搜索算法可以很好地解决这一问题。相比RD和GR算法,BP算法在较少的迭代次数就可以得到较好的初始解。同时,BP算法在运行时间上也优于PSO和GA,本文算法对于TSP有较高的求解质量。下一步工作将在信息传播算法求解TSP的时间复杂度和空间复杂度上进行研究,并探讨如何提高TSP的效率和准确率。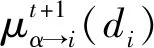
2 求解TSP的信息传播算法
2.1 TSP的线性规划方程
2.2 TSP的因子图

2.3 TSP的算法优化
2.4 模拟退火算法
2.5 局部搜索

3 数值实验及分析
3.1 初始化性能对比分析



3.2 求解时间对比分析



3.3 求解质量对比分析


4 小结

