混合复合层材料增强金属内衬圆柱壳失效机理研究

王文才,杨福江

(核工业理化工程研究院，天津 300180)

0 引言

在压力容器、火箭发动机或者离心分离等领域，传统的金属圆柱壳结构已经不满足高压、高强、抗震等更高要求，而纤维复合材料已广泛应用于航空、航天、造船、桥梁、石油、化工等领域[1-5]，由于纤维复合材料具有轻质高强、耐腐蚀、易成形、易维修等特点，是制造一些圆柱壳结构较为理想的增强材料。目前较为常见的圆柱壳形式是玻璃纤维加金属、碳纤维加金属或者碳纤维和玻璃纤维加金属等，其中复合材料层有些是带螺旋角度缠绕，有些是环向缠绕，根据实际工作条件，具体铺层形式不一[6-8]。本文研究对象为玻璃纤维加碳纤维增强金属内衬圆柱壳，其中玻璃纤维和碳纤维均为环向缠绕成型，该混合复合层材料增强金属内衬圆柱壳主要应用于旋转机械和压力容器行业。传统的金属圆柱壳设计是根据给定的工艺尺寸和工作条件，并参考制造、安装和检修要求，进行应力分析，确定结构形式和尺寸。对于复合材料增强圆柱壳的设计，由于复合材料本身的可设计性，使圆柱壳设计的起点从结构设计转变成材料铺层设计，因此设计的合理性和正确性显得尤为重要，需要开展混合复合层材料增强金属内衬圆柱壳在离心旋转载荷下的力学性能、破坏机理等许多机理性基础研究。传统分析主要是针对内压、外压、轴压等状态下的失稳及破坏研究[9-12]。本文主要针对旋转分离用圆柱壳结构，，建立在离心旋转载荷条件下的应力计算方法，并进行试验验证；同时，考虑金属屈服后视为双线性问题，建立各层应力与爆破压力关联性方程；最终理论结合试验确定圆柱壳失效机理。

1 混合复合层材料增强金属内衬圆柱壳应力计算

1.1 计算方法

借助Ansys有限元软件进行圆柱壳应力分析，采用轴对称183单元进行建模，同时考虑材料非线性(考虑材料的塑性应力应变关系)、状态非线性(复合材料层和金属内衬的接触问题)以及离心载荷[13-14]。其中，在对金属内衬施加预应力计算时，采用复合材料降温法进行模拟。

1.2 计算参数

1.2.1 材料参数

金属内衬材料参数：弹性模量E=70 GPa，泊松比υ=0.3，密度ρ=2 800 kg/m3，屈服强度σ0.2=450 MPa；玻璃纤维材料参数：纵向模量E1=65 GPa，横向模量E2=8 GPa，剪切模量G12=5 GPa，主泊松比υ12=0.3，密度ρ=2 000 kg/m3，纵向强度σ1=2 000 MPa；碳纤维材料参数：纵向模量E1=140 GPa，横向模量E2=8.5 GPa，剪切模量G12=6 GPa，主泊松比υ12=0.3，密度ρ=1 600 kg/m3，纵向强度σ1=2 600 MPa。以上数据均为自测数据。

1.2.2 几何参数

圆柱壳内半径r=85 mm；圆柱壳从内到外依次是金属内衬厚度为2 mm，玻璃纤维层厚度为1 mm，碳纤维层厚度为1.8 mm，玻璃纤维和碳纤维均为环向缠绕成型。

1.3 计算结果验证

首先，按照Ansys有限元计算方法计算出旋转过程中不同载荷下圆柱壳的径向变形，然后，通过测量圆柱壳在不同旋转载荷下的真实变形，来验证应力分析理论计算模型的正确性。理论计算和试验结果如表1所示，可以看出，理论计算值与实测值基本吻合，说明上述的计算方法正确可用。

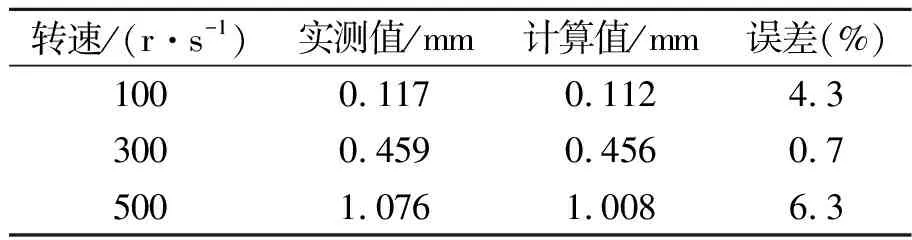
表1 不同转速下圆柱壳径向变形计算值和实测值对比Tab.1 Comparison of calculated and measured radial deformation values of cylindrical shells under different rotational speeds

2 混合复合层材料增强金属内衬圆柱壳失效机理研究

混合复合层材料圆柱壳采用玻璃纤维和碳纤维复合材料增强金属内衬结构，其中金属层为刚度层，满足圆柱壳旋转时要有较高轴向刚度的要求；玻璃纤维复合材料主要为金属层施加预应力，以降低其在额定载荷下的应力；碳纤维复合材料起到施加小部分预应力和保护内部金属内衬和玻璃纤维复合材料的作用，为主要承力层。在不考虑材料性能退化的情况下(金属视为弹性材料)，圆柱壳各层环向应力随转速升高的变化曲线如图1所示。

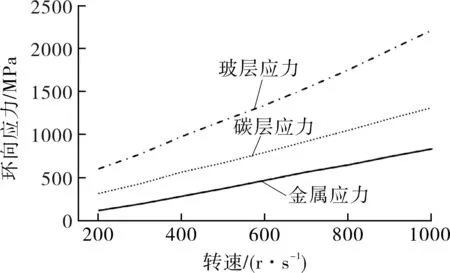
图1 圆柱壳各层应力随转速升高的变化曲线Fig.1 Variation curves of stress in each layer of cylindrical shell with increasing rotational speed

由图1可以看出，随着转速的升高，各层应力都在增加，碳纤维层应力增加速率最快，但是当转速达到600 r/s左右时，金属层应力首先达到其屈服强度450 MPa，而此时玻璃纤维复合材料层应力为790 MPa左右，碳纤维层应力为1 340 MPa左右，都还未达到各自的断裂强度。

为了讨论金属内衬的屈服对圆柱壳失效的影响，还需要进行深入分析。金属层达到屈服临界点时，对应的应变约为0.64%，远未达到其断裂应变(4%)，同时又由于金属层在圆柱壳内侧，为受限材料，其变形受外层复合材料限制，也就是说虽然金属层已经屈服，但此时复合材料层应力还未达到其断裂强度，圆柱壳整体结构不会发生明显宏观破坏。考虑到金属层达到屈服强度后会进入塑性阶段，弹性模量会发生下降，假设材料特性为双线性，当铝合金进入屈服后，其切线模量降为3 GPa。圆柱壳复合材料各层环向应力随转速的变化情况如图2所示。

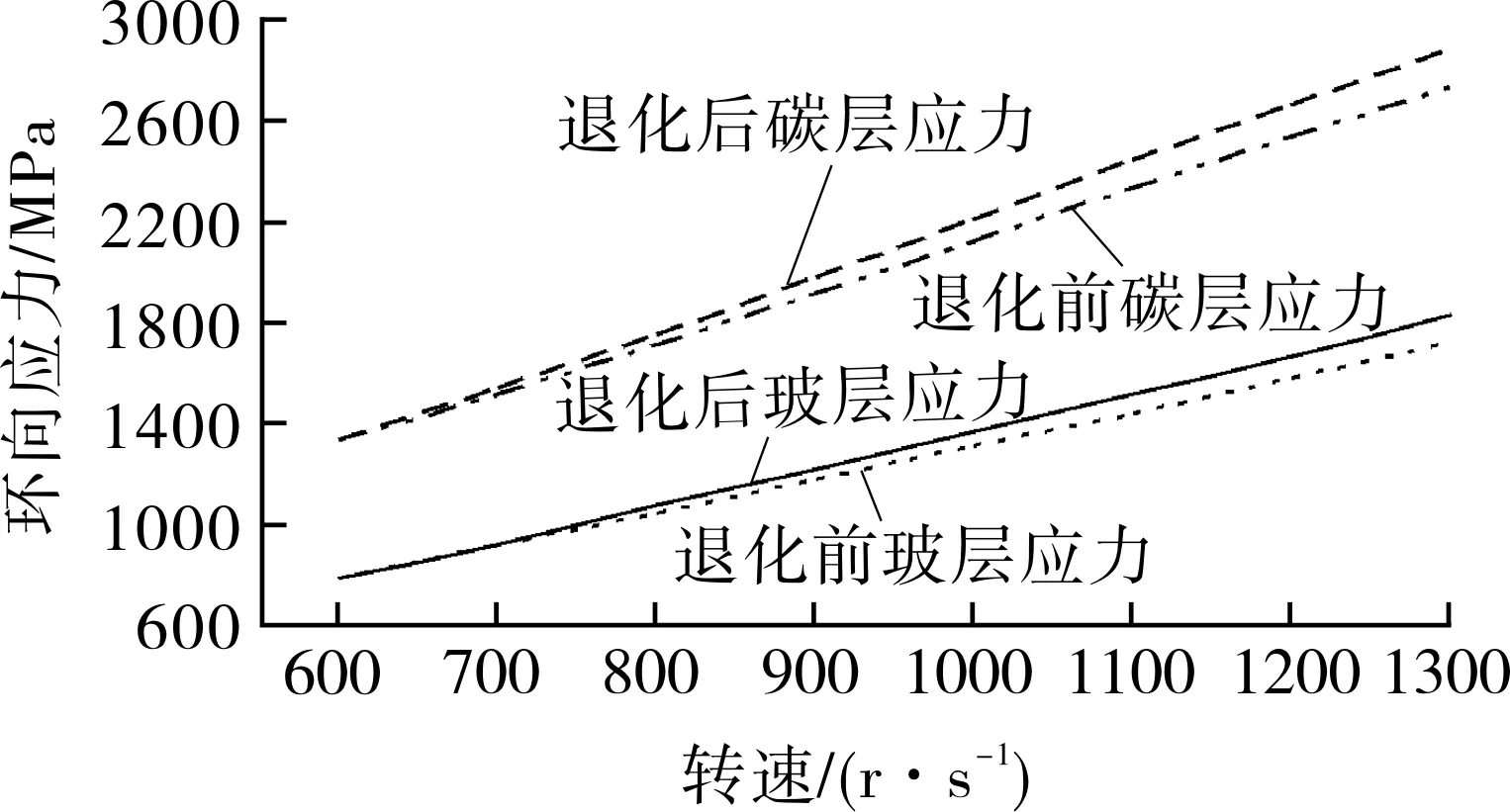
图2 考虑金属屈服进入塑性后各层应力随转速 升高的变化曲线Fig.2 The variation curves of stress in each layer with the increase of rotational speed after considering metal yield entering plasticity

由图2可以看出，金属材料屈服进入塑性后，材料性能的退化导致玻璃纤维层和碳纤维层应力会迅速增大，目前玻璃纤维复合材料极限强度能达到2 000 MPa以上，碳纤维复合材料极限强度在2 600 MPa左右，由此可见，随着转速的增加，按照最大应力准则，碳纤维复合材料层会先于玻璃纤维层达到极限强度而发生破坏。

由以上理论分析研究得出，混合复合层材料增强金属内衬圆柱壳在旋转载荷条件下的失效机理为：随着转速增加，金属内衬先发生屈服，材料性能退化，引起复合材料层应力迅速增加，圆柱壳最终由于碳纤维复合材料层达到其极限强度而失效。

3 验证试验设计

3.1 爆破试验

受试验条件限制，圆柱壳在超高旋转载荷状态下失效后基本为粉末状，无法观测哪层先破坏。为了验证混合复合层材料增强金属内衬圆柱壳的失效机理的理论分析是否正确，考虑通过爆破试验进行更直观的验证性研究。当在旋转载荷下圆柱壳的应变与压力产生应变一致时，两种载荷施加给各层的应力均为环向应力。利用应变相等原则，将旋转载荷与压力结合起来，首先，将金属层屈服后视为双线性考虑，通过有限元数值计算出圆柱壳各层在不同旋转载荷下的应变；然后，通过公式得到应变对应压力p；最后，通过应变将应力与压力联系起来，参考公式依次如下：

pr=E1ε1t1+E2ε2t2+E3ε3t3

(1)

式中，p为压力；r为圆柱壳半径；E1，E2，E3分别为金属、玻璃纤维复合材料和碳纤维复合材料的纵向模量；ε1，ε2，ε3分别为金属层进入屈服前金属、玻璃纤维复合材料和碳纤维复合材料的应变；t1，t2，t3分别为金属、玻璃纤维复合材料和碳纤维复合材料的厚度。

式(1)是金属层在弹性阶段时的计算公式，此时金属未屈服。

pr=E1ε1t1+E′1(ε′1-ε1)t1+E2ε′2t2+E3ε′3t3

(2)

式中，E′1，ε′1，ε′2，ε′3为金属层进入屈服后的切线模量和各层应变。

式(2)是金属进入屈服后的计算公式，此时的ε1为金属内衬刚进入屈服点时的应变。

由式(1)(2)可以计算得到不同旋转载荷对应的内压力，再利用式(3)[15]可以得到圆柱壳的环向应力。

σ=pr/t

(3)

式中，σ环向应力；t为圆柱壳壁厚。

前面理论研究表明，圆柱壳最终是碳纤维复合材料层先达到强度极限而失效，因此，结合本节计算，考虑金属屈服进入塑性条件后，可以得到碳纤维复合材料层环向应力随压力增大的变化曲线，具体如图3所示。

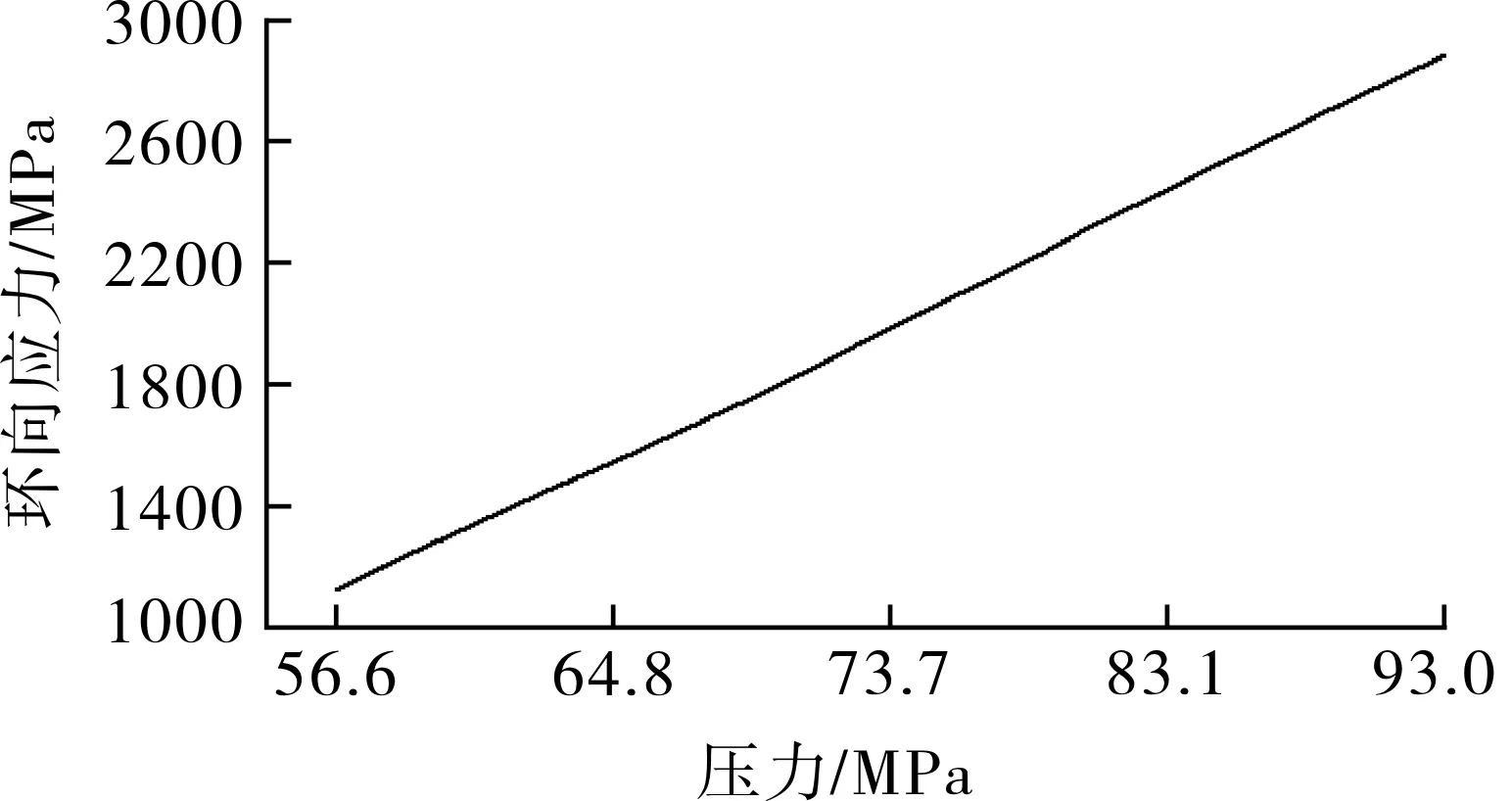
图3 圆柱壳碳纤维层应力随压力增加的变化曲线Fig.3 Variation curve of stress of carbon fiber layer of cylindrical shell with increasing pressure

将理论数据进行曲线拟合，可以得到关于压力与碳纤维环向层应力的关系式:

y=48.485x-1604.9，R2=0.9995

(4)

同时也可以拟合出压力与玻璃纤维环向层应力的关系式：

y=32.083x-1149.5，R2=0.9997

(5)

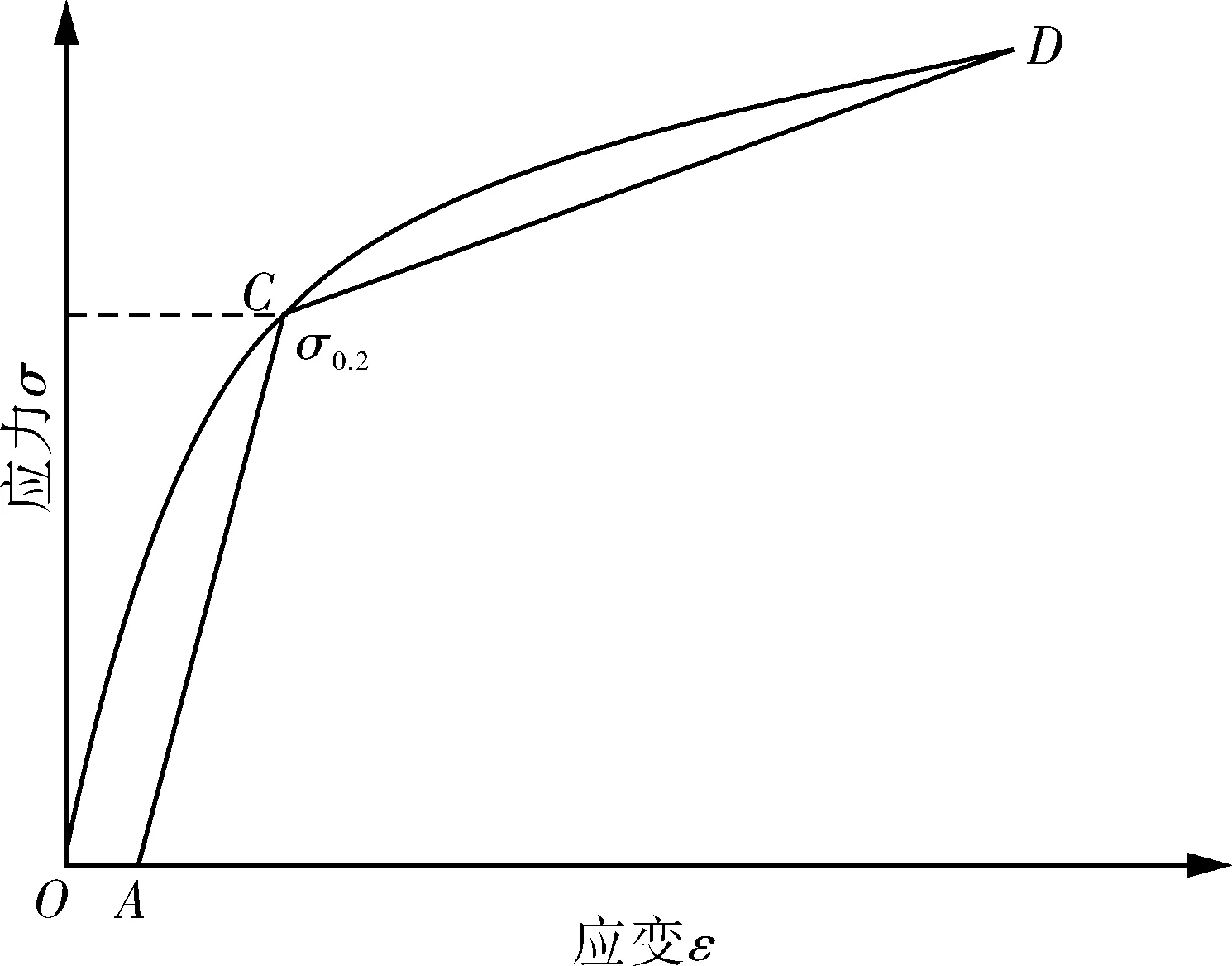
图4 应力-应变曲线计算与实际状态的对比示意Fig.4 Comparison between the calculated and the actual state of stress-strain curve

存在问题如下：在计算中假设金属材料性质为双线性材料，如图4中的AC和CD段(图中的弧线段为真实的应力应变曲线示意图)，在实际中，随着金属材料进入塑性屈服阶段，其圆柱壳模量并不是按照双线性在屈服点有个突变，而是缓慢降低，因此，随着转速或者试验压力的提高，金属材料过屈服点一段时间后模量才会发生比较大的降低，在CD段初始阶段，计算采用的模量要低于实际模量[16]，理论预测的失效转速或压力会与实际有一定误差。

3.2 试验结果

采用FST5000-0-AZ2-36/323型爆破实验台，应变测量设备为UCAM-60B应变仪。试验结果如表2所示。

以上由试验得到的σ复材,E复材包括玻璃纤维层和碳纤维层，需要通过式(6)进一步计算得到碳纤维复合材料环向层应力。

σ碳=(3σ复材-σ玻)/2

(6)

将爆破压力代入到式(4)(5)中,可以得到爆破时玻璃纤维复合材料和碳纤维复合材料环向应力。表3列出了通过爆破压力理论计算得到的碳纤维环向强度与试验计算值的对比。

表2 圆柱壳的爆破试验数据Tab.2 Blasting test data of cylindrical shell

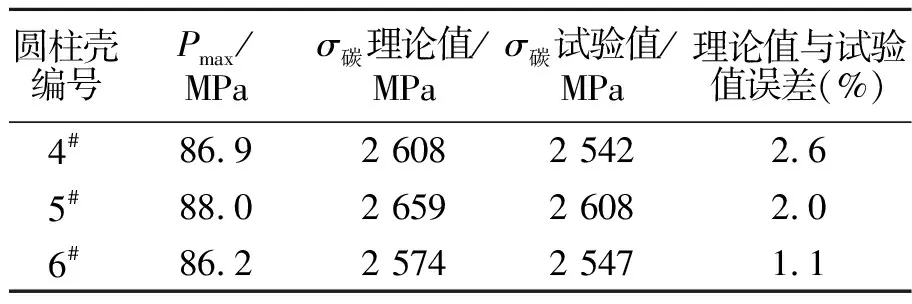
表3 碳纤维环向强度理论值于试验值对比Tab.3 Comparison between theoretical and experimental values of carbon fiber annular strength

由表3可以看出，通过爆破压力计算得到的碳纤维环向强度与试验结果相差不大，也就是说当碳纤维复合材料环向强度一定时，理论预测的爆破压力与试验值基本吻合，这也间接说明混合复合层圆柱壳最终由于碳纤维复合材料层达到其极限强度而失效。通过爆破试验后圆柱壳失效照片(见图5)也可以看出，圆柱壳是由于外层碳纤维复合材料达到强度极限而引起失效，进而对金属内衬失去保护作用，最终应变增大、导致整体失效。

图5 圆柱壳爆破失效后的情况Fig.5 Conditions after blasting failure of cylindrical shell

4 结论

(1)利用有限元法计算了混合复合层材料增强金属内衬圆柱壳的应力状态，并通过了试验验证，理论模型计算结果与试验结果基本吻合。

(2)通过理论分析，随着载荷的增加，金属内衬应力首先达到屈服强度，并考虑金属屈服后的影响，最终碳纤维复合材料层会先于玻璃纤维层达到极限强度而发生破坏。

(3)建立了圆柱壳复合材料各层应力与爆破压力关联性方程，明确了混合复合层材料增强金属内衬圆柱壳随着载荷增加，为外层碳纤维复合材料达到强度极限而引起整体失效的失效机理，并得到了爆破试验验证。