考虑声衰减和声频散的聚乙烯超声相控阵缺陷检测仿真模型

方海清，施建峰,2,3，郑津洋,2,3

(1.浙江大学 化工机械研究所，杭州 310027;2.高压过程装备与安全教育部工程研究中心，杭州 310027;3.流体动力与机电系统国家重点实验室，杭州 310027)

0 引言

聚乙烯(PE)管具有耐腐蚀、韧性好、使用寿命长等优点，在石油和燃气等领域已有数十年的成功应用经验[1]，近年来逐渐应用于核电站冷却水输送系统，如我国三门核电站30 in冷却水输送管道[2]；美国的Callaway核电站36 in冷却水输送管道[3]。大壁厚PE管的生产工艺和焊接过程复杂，导致管道和焊缝存在缺陷的可能性增加[4-5]。因此，为确保PE管道服役期间的安全运行，借助无损检测技术进行大壁厚PE管的缺陷检测至关重要[6-7]。

超声相控阵检测技术作为主要的无损检测方式之一，已广泛应用于金属管和PE管[8-10]。与金属材料不同，PE具有声衰减和声频散特性。相关研究[11]表明，在常用的超声检测频段上，PE的声衰减系数与频率线性相关，声衰减系数和相速度均随频率的增大而增大，如图1(a)所示。当复合频率超声信号在PE中传播时，由于不同频率组分的声衰减系数和相速度不同，信号频谱向低频方向移动[12]，导致波形畸变。通用的超声相控阵检测技术采用固定的群速度设计延时法则，未考虑波形畸变的影响，在对PE检测时，各阵元在焦点处会产生畸变程度不同的声压信号，叠加效果无法最大化[13]，如图1(b)所示。当检测深度较大时，信号畸变严重，导致聚焦的焦柱直径大，检测信噪比低。

国内外一些学者对超声信号在PE中的传播规律展开研究。PIERCE等[14]认为声波的损耗与松弛有关，利用热黏性波动方程来表征介质中的声衰减。SZABO等[15]借鉴了电磁波声耗散项的形式，在理想波动方程的基础上，引入了卷积积分项来表征声波的耗散。侯东圣等[16]在SZABO模型的基础上，利用时域有限差分法获取了PE超声相控阵检测声场中任意一点在任意时刻的声压信号。

这些研究为超声信号在PE中的传播规律提供了理论基础和求解方法，但在PE超声相控阵缺陷检测仿真计算中，还需考虑超声信号多次散射和反射作用对缺陷成像的影响。目前，通用的PE超声相控阵缺陷检测仿真方法未考虑超声信号不同频率组分的声衰减系数和相速度差异[17-18]，模拟信号的频谱和波形变化与实际不符，随着缺陷埋藏深度的增加，模拟结果的准确性会逐渐降低。

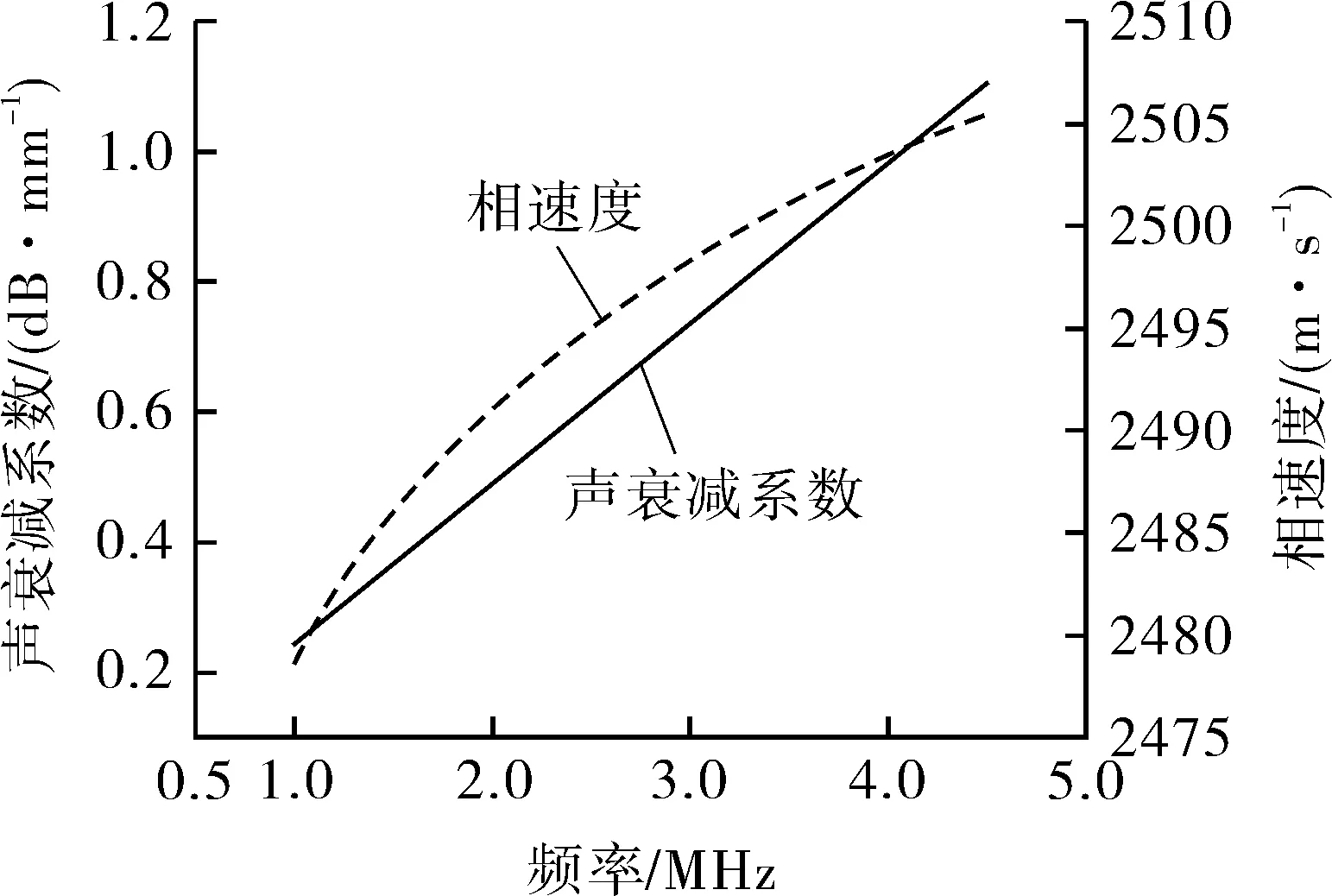
(a)PE声衰减和声频散特性[11]

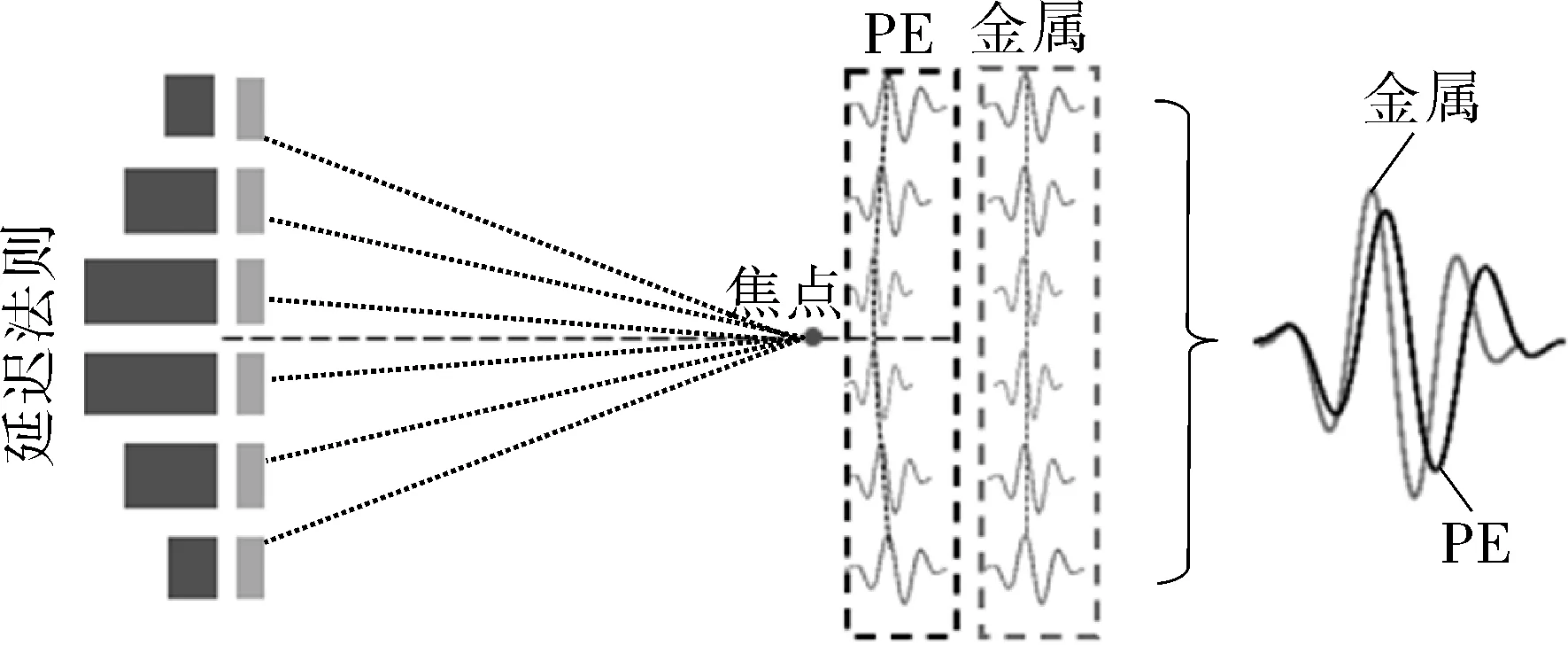
(b)聚焦效果对比[13]图1 PE声学特性对超声波传播的影响Fig.1 Influence of PE acoustic characteristics on ultrasonic propagation

为此，提出一种复合频率超声信号传播模型，对比分析不同频率组分的声衰减系数和相速度为变量、声衰减系数和相速度为常量两种情况下缺陷模拟结果的差异。最后，为验证模型有效，考虑复合频率超声信号传播的群速度随检测深度变化规律，改进超声相控阵检测的延时聚焦法则，并应用于大壁厚PE管超声相控阵检测中。

1 复合频率超声信号传播模型

1.1 单频超声波的波动方程

理想波动方程是超声相控阵检测技术的理论基础，仅适用于各向同性、均匀且无传播损耗材料[19]，如式(1)所示。

(1)

式中,c为声速,m/s；P为声压,Pa;t为传播时间,s;x为一维空间中各点位置,m。

由于PE的声频散和声衰减特性，超声波在PE中传播时，随着传播距离的增加，声能逐渐减小且波形发生畸变。为此，在式(1)的基础上，引入变量Q来衡量PE内各点对声压的损耗:

(2)

对零初始相位的单频超声波，一维空间中各点波动方程满足式(3)[20]。

P=P0e-αωxsin(ωt-kx)

(3)

式中，P0为原点声压，Pa；αω为频率ω对应的声衰减系数，1/m；ω为超声频率，Hz；k为波数，1/m。

通过式(2)和式(3)可知，变量Q需满足式(4)的条件。

(4)

其中：Pt=∂P/∂t。

式中，cω为频率ω的超声波传播相速度，m/s。

假设材料各向同性，超声波在材料内部沿各个方向的衰减均相同，可将式(2)扩展到二维或三维形式，因此PE材料中单频超声波的波动方程可以表示为：

(5)

已有研究[15,21]证明，在常见的超声检测频率范围内，各频率超声波对应的声衰减系数和相速度可通过式(6)近似计算。

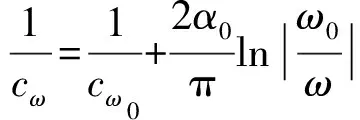
(6)

式中,cω0为频率为ω0的超声波传播相速度,m/s；α0为声衰减系数和频率的比例系数，1/(m ·Hz),α0=4.5×10-61/(m·Hz);ω0为参考频率,Hz。

1.2 复合频率超声信号的数值处理方法

在超声相控阵检测中，各阵元发射的复合频率超声信号s可用Morlet小波表示[22]，表达式如下：

(7)

式中,A为信号幅值,Pa;θ为-6 dB带宽相关量,s;f0为复合频率超声信号中心频率,Hz；Δf为-6 dB带宽,Hz。

根据傅里叶级数相关原理，复合频率超声信号可转化为单频信号的叠加，如式(8)所示。

(8)

式中,Aω为频率ω处的幅值;φω为频率ω处的相位。

由于Morlet小波双边频谱为偶函数、相位谱为中心对称函数，式(8)可简化为：

(9)

通过式(9)，选取适当数量的单频信号进行叠加，即可实现对复合频率超声信号的拟合，如式(10)所示。

(10)

式中，s′为拟合检测信号；n为单频信号数量；Ai为第i个信号的幅值；ωi为第i个信号的频率；φi为第i个信号的相位。

设置各单频信号的声衰减系数和相速度，通过式(5)计算并叠加各单频信号的传播规律，等效为复合频率超声信号的传播规律。

2 超声相控阵缺陷检测仿真方法及试验设计

2.1 缺陷检测的有限元仿真

设置PE密度ρ为976 kg/m3，创建36 mm×30 mm的二维几何模型如图2所示，在深度为10,20 mm处设置半径为1 mm的孔洞缺陷。探头固定在模型上边界中心，探头阵元数量为32，阵元间距和间隙分别为0.9 mm和0.1 mm。

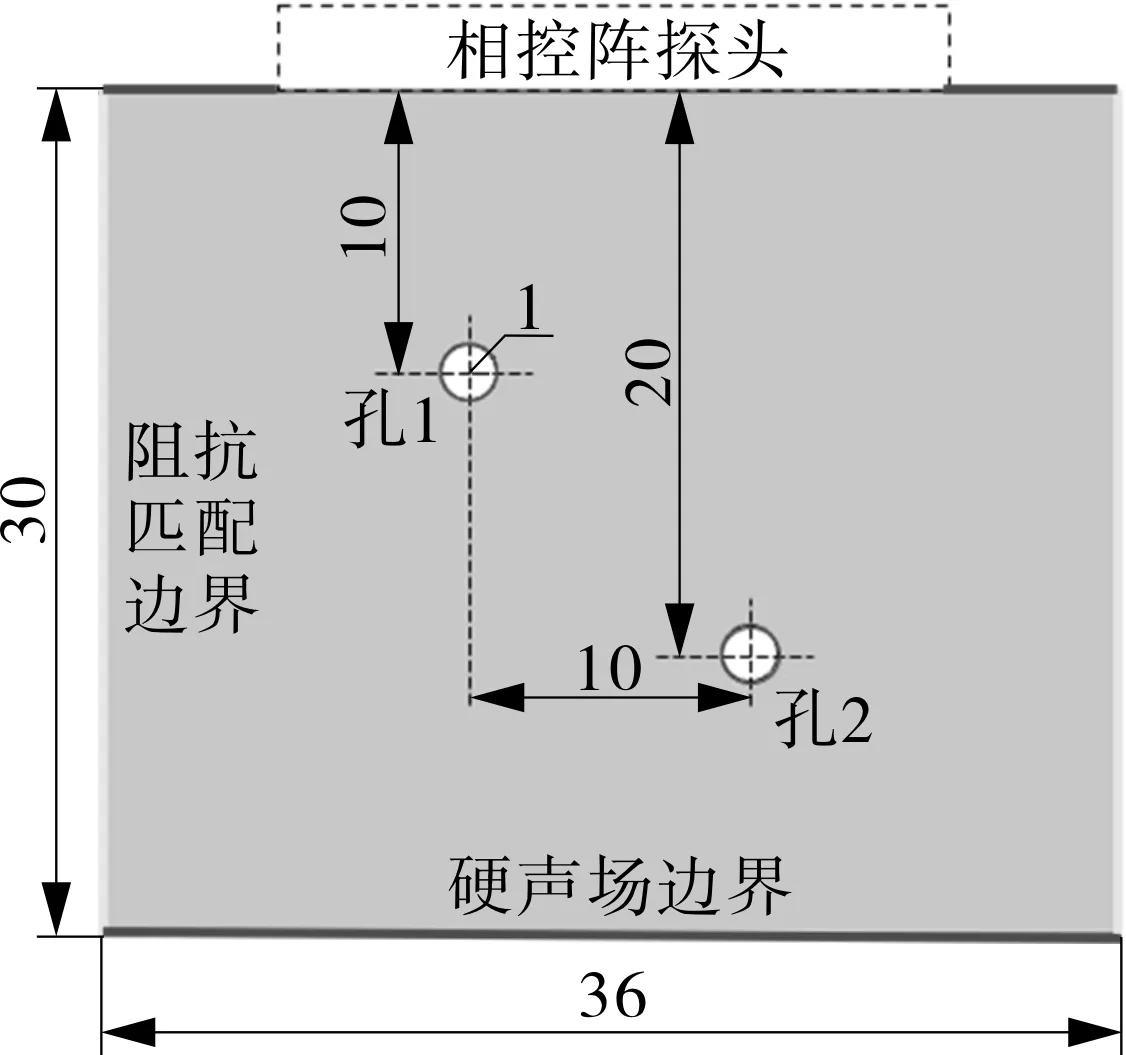
图2 有限元几何模型Fig.2 Finite element geometric model

为真实反映PE管边界对超声相控阵检测的影响，模型边界条件设置如图2所示。模型两侧为阻抗匹配边界，对应较长PE管的轴向方向，无信号反射；未被阵元覆盖的上边界、下边界和孔洞缺陷边界均为硬声场边界，对应PE管外壁面和内壁面，能完全反射信号。

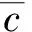
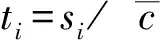
τi=max(t)-ti

(11)

式中,si为第i个阵元中心与焦点的距离,m;τi为第i个阵元的延迟时间,s。

将中心频率为2.0 MHz，-6 dB带宽为50%的复合频率超声信号进行分解，在0.5～5 MHz之间，每隔0.2 MHz取对应频率信号，使用有限元软件COMSOL Multiphysics®5.2计算并叠加各单频信号的模拟结果，等效为复合频率超声信号的模拟结果。

为对比分析不同频率组分的声衰减系数和相速度为变量、声衰减系数和相速度为常量两种情况的缺陷仿真效果，分别设置各频率信号的声衰减系数和相速度。

(1)不同频率组分的声衰减系数和相速度为变量时，取式(6)中的参考频率为2.5 MHz，该频率超声信号的相速度为2 495 m/s[11]，计算各频率信号对应的声衰减系数和相速度。

(2)声衰减系数和相速度为常量时，各频率信号的声衰减系数均与中心频率(复合频率超声信号的中心频率)信号的声衰减系数相同，且各频率信号的相速度均为2 400 m/s。

超声相控阵缺陷检测的有限元模拟步骤如图3所示。利用有限元计算各阵元随时间变化的声压值，作为接收信号；再使用延时法则，将孔径内各阵元接收信号沿扫查线(孔径中心与焦点所在直线)合成；并通过插值算法，计算扫查线之间区域的声压分布，最后生成缺陷检测模拟图像。

2.2 试验设计

为分析PE超声相控阵缺陷检测模拟结果，设计与模型参数相同的对比试验。从PE管取样，加工如图4(a)所示的PE试块，SIUI相控阵检测设备与2.0L32-1.0-10探头如图4(b)所示，超声相控阵检测参数与仿真设置完全相同。

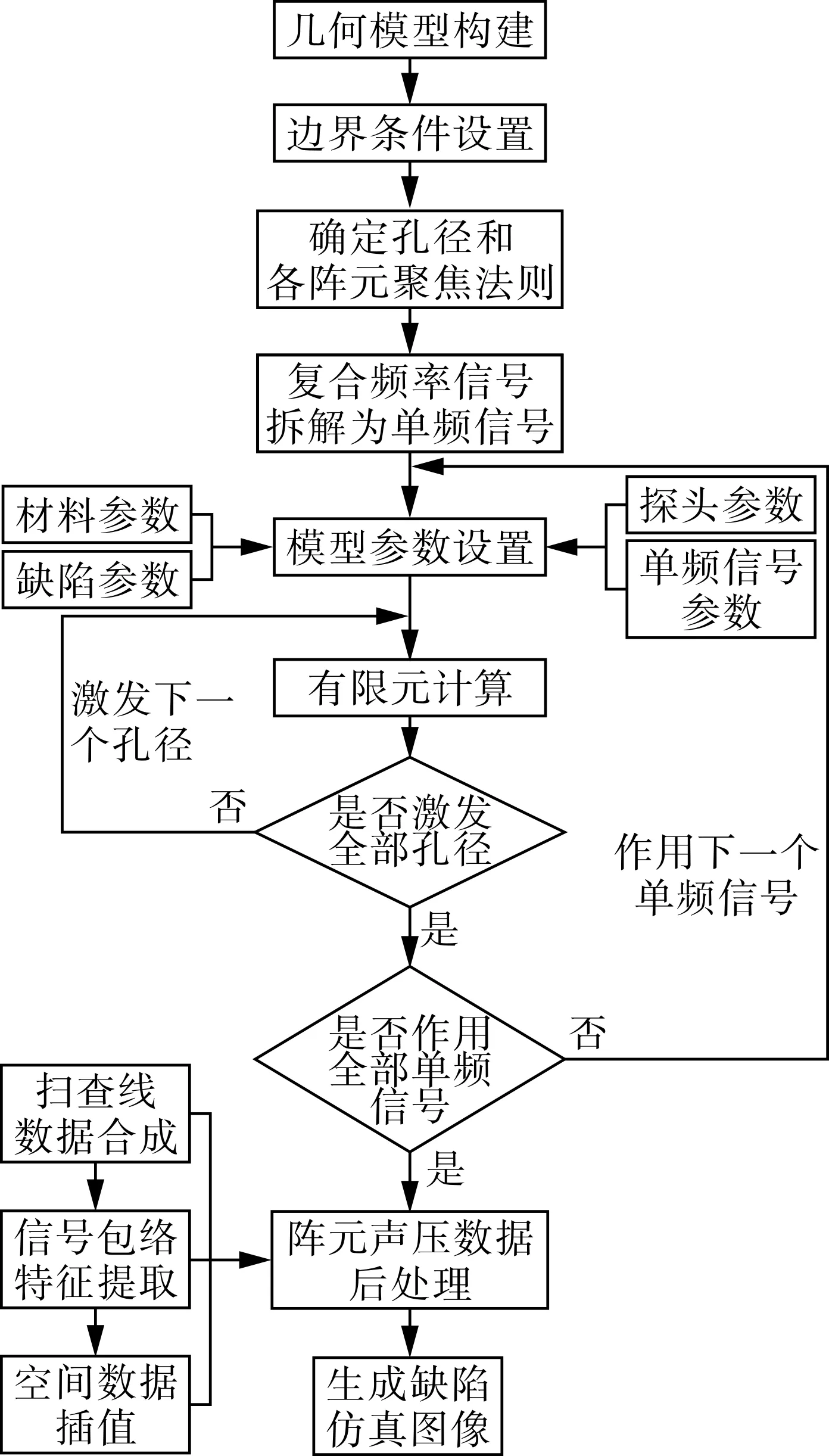
图3 缺陷检测有限元模拟步骤Fig.3 Basic steps of finite element simulation for defect detection

(b)超声相控阵设备和探头图4 孔洞缺陷的超声相控阵检测试验Fig.4 Ultrasonic phased array testing of hole defects

3 结果分析和讨论

3.1 缺陷成像特征对比

在通用延时法则作用下，获取不同频率组分的声衰减系数和相速度为变量、声衰减系数和相速度为常量两种情况的超声相控阵缺陷检测模拟结果和试验检测结果并分别将其归一化处理，生成如图5(a)(b)(c)所示的缺陷图像，图像颜色与数字的映射关系如图5(f)右侧的图注所示。由于使用二维模型做近似仿真，将试块中的横通孔等效为模型中的孔洞缺陷，会减弱横通孔对信号的反射作用。对于非聚焦区域的孔洞缺陷，由于所处深度较浅，各阵元超声信号抵达此处时，能量衰减小，聚焦效果差，在横通孔的反射作用下会产生明显的伪像信号，因此图5(a)(b)中的孔洞缺陷周围的伪像信号强度明显小于实际检测图像；对于聚焦区域的孔洞缺陷，由于所处深度较深，信号能量衰减大，经横通孔反射产生的伪像信号十分微弱，图像显示不明显，但在该位置处的聚焦效果好，可以产生明显的缺陷信号，两种情况的模拟结果均与试验检测结果一致。

将两种情况的模拟结果与试验检测结果在空间各点产生的归一化声压作差，绝对误差如图5(d)～(f)所示。比较图5(d)(e)，对比相同位置处的缺陷信号，考虑PE声衰减和声频散特性的模拟结果与实际检测结果误差更小。由于在复合频率超声信号传播过程中，受PE声衰减和声频散特性影响，信号频谱会向低频方向移动，导致声衰减效果随之降低。因此，随着深度的增大，不同频率组分的声衰减系数和相速度为变量、声衰减系数和相速度为常量两种情况的声衰减累积偏差逐渐增大，声压差距也逐渐增加，如图5(f)所示。

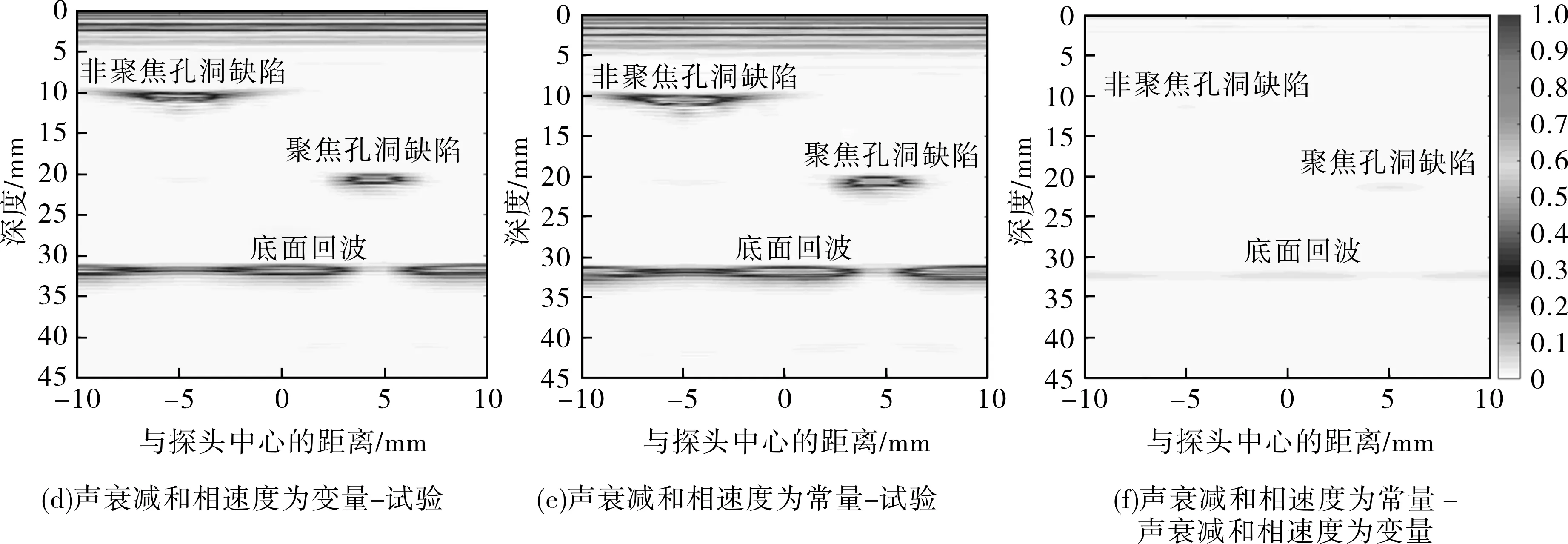
图5 缺陷仿真及试验检测成像及对比Fig.5 Imaging and comparison of defect simulation and experimental detection

3.2 缺陷信号强度对比

取图5(a)～(c)中两缺陷所在竖直线(x=-5,5 mm)上的信号，并按直线上的底面回波信号归一化比例对信号整体进行缩放，处理后的信号分布如图6所示，两图图例相同。声衰减系数和相速度为常量时，声衰减效果更明显，因此两缺陷信号幅值最大。当声衰减系数和相速度为变量时，由于模拟信号带宽相对实际检测信号更大，当检测深度较浅时，高频衰减更剧烈，整体衰减效果更明显，因此非聚焦区域处缺陷信号幅值较大；随着检测深度的增加，信号频带越宽，频谱左移速度越快[12]，模拟信号的高频部分会逐渐少于实际检测信号，整体衰减效果减小，因此在聚焦区域处缺陷信号幅值反而小于试验结果。

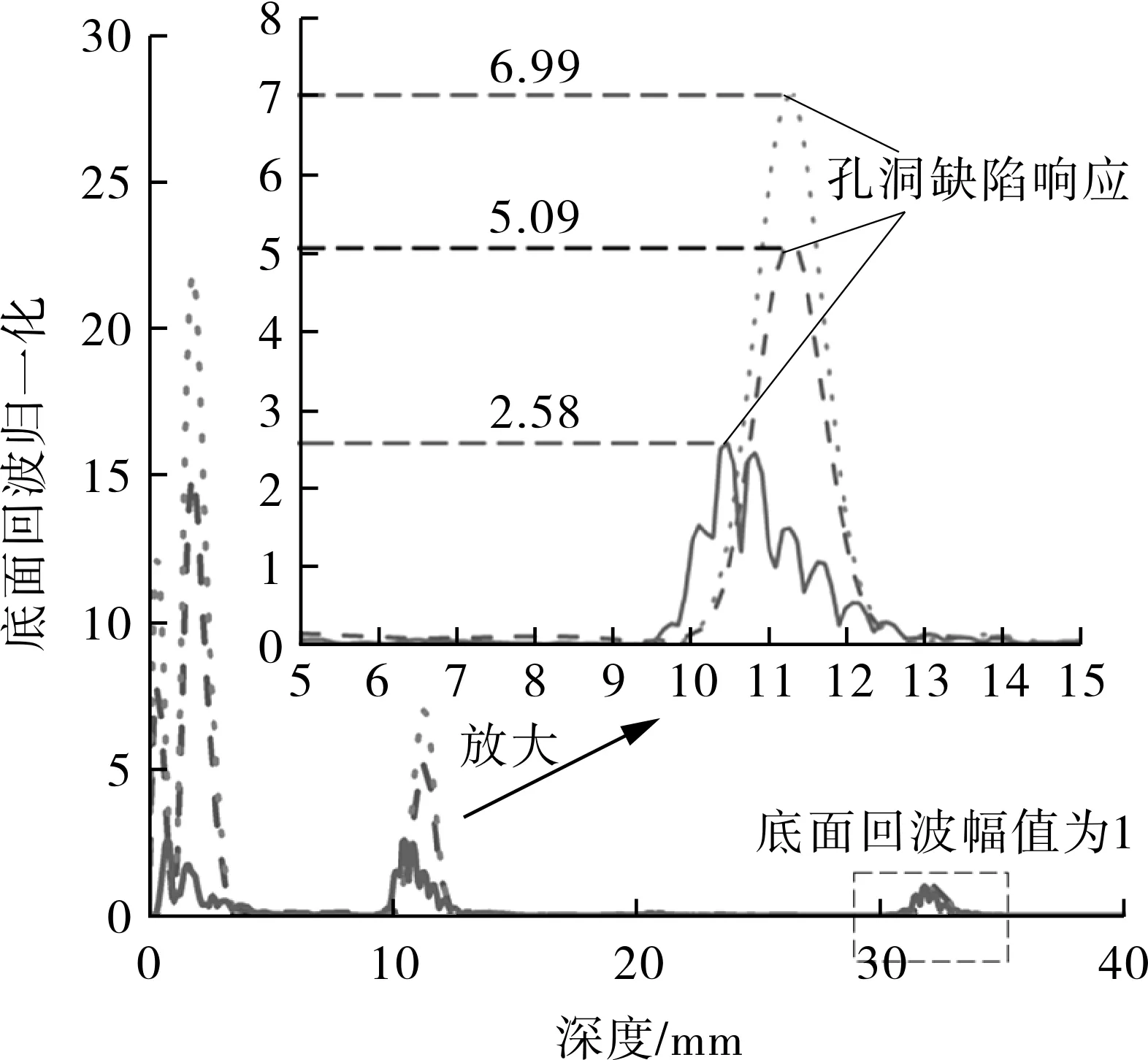
(a)竖直线x=-5 mm上的声压

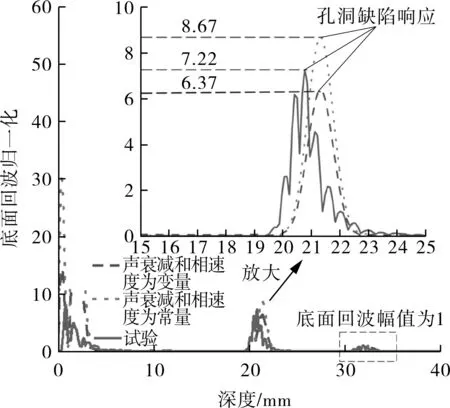
(b)竖直线x=5 mm上的声压图6 缺陷竖直线方向声压分布Fig.6 Sound pressure distribution along vertical line of defect

综上所述，考虑不同频率组分的声衰减系数和相速度为变量时，模拟结果中两缺陷处信号幅值与试验检测结果更接近，聚焦区域的孔洞缺陷信号幅值偏差为11.77%。考虑到实际PE材料、孔洞缺陷和检测信号等均无法与理论完全保持一致，可以认为该模型对PE超声相控阵缺陷检测有较好的模拟效果。

4 改进的延时聚焦法则及其检测效果

4.1 基于复合频率超声信号传播模型的改进延时聚焦法则

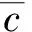
为进一步验证复合频率超声信号传播模型的有效性，考虑复合频率超声信号在PE中传播的群速度随检测深度变化规律，改进超声相控阵检测的延时聚焦法则，使各阵元在焦点处产生的声压信号波峰相对应，增强聚焦效果。记阵元i与焦点的距离为Si，假设材料各向同性，为简化模型复杂度，提高计算效率，可根据图7(a)中阵元与焦点的距离，建立如图7(b)所示的一维模型。阵元i发射信号波峰与焦点处信号波峰的时间差值ti，即为超声波从阵元i传播到焦点所需时间，再通过式(11)即可计算改进后的延时法则。

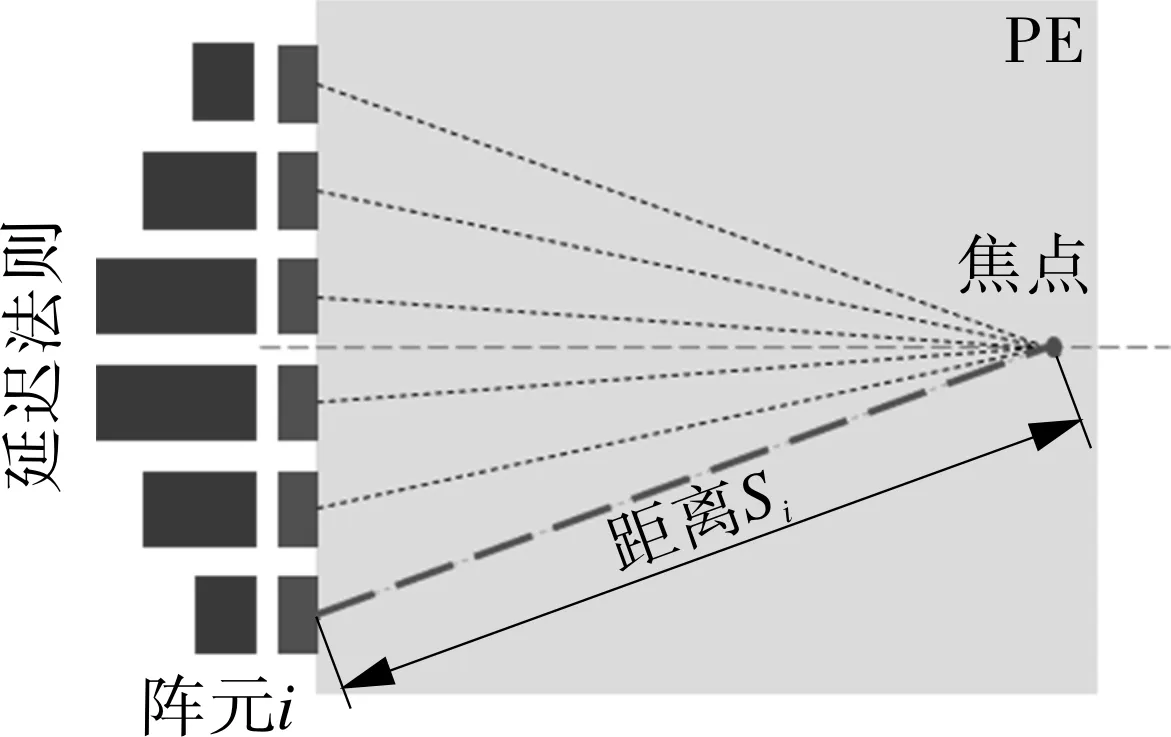
(a)延时聚焦

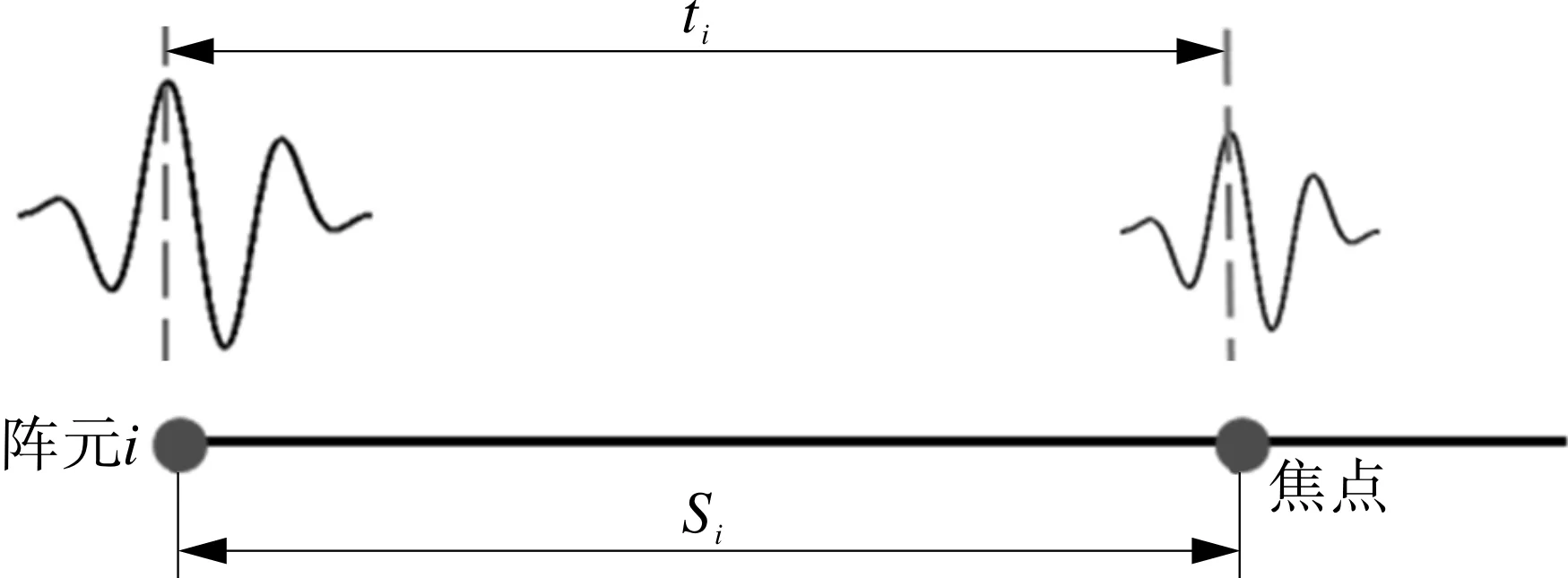
(b)一维模型图7 改进延时法则计算Fig.7 Improved delay rule calculation

4.2 厚壁HDPE管道检测效果验证

为验证模型有效，将改进的延时法则应用于实际检测，如图8所示。使用SIUI相控阵检测设备和2.0L32-1.0-10相控阵探头，对外径为813 mm,壁厚为74 mm的PE管检测，相控阵聚焦半径与管道壁厚相同。

图8 大壁厚PE管超声相控阵检测Fig.8 Ultrasonic phased array detection of large wall-thickness PE pipe

在相同检测环境下，分别使用通用的延时法则和改进的延时法则，对大壁厚PE管进行超声相控阵检测。比较聚焦区域和非聚焦区域的缺陷回波信号幅值来分析两种延时法则对检测结果的影响。为消除信号不稳定引起的误差，对多组检测数据中的缺陷回波信号幅值进行显著性分析，发现在显著性水平为0.05的情况下，改进的延时法则可使聚焦区域的内壁面回波信号增强5.1%，使非聚焦区域的缺陷信号增强6.1%，如图9所示。

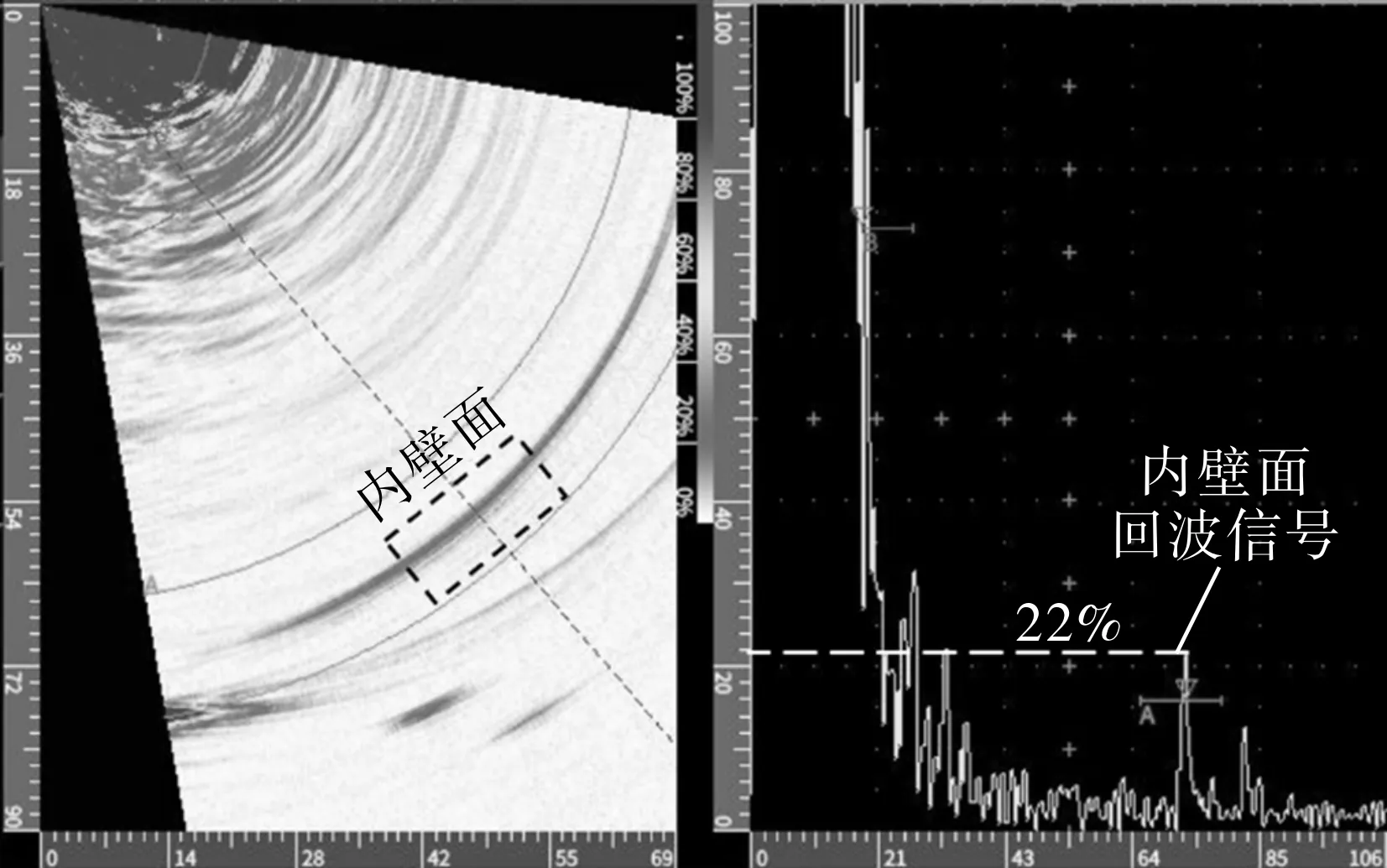
(a)通用的延时法则(内壁面回波信号)

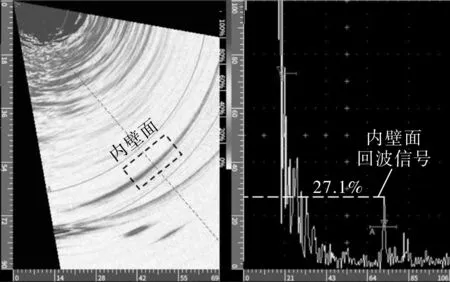
(b)改进的延时法则(内壁面回波信号)

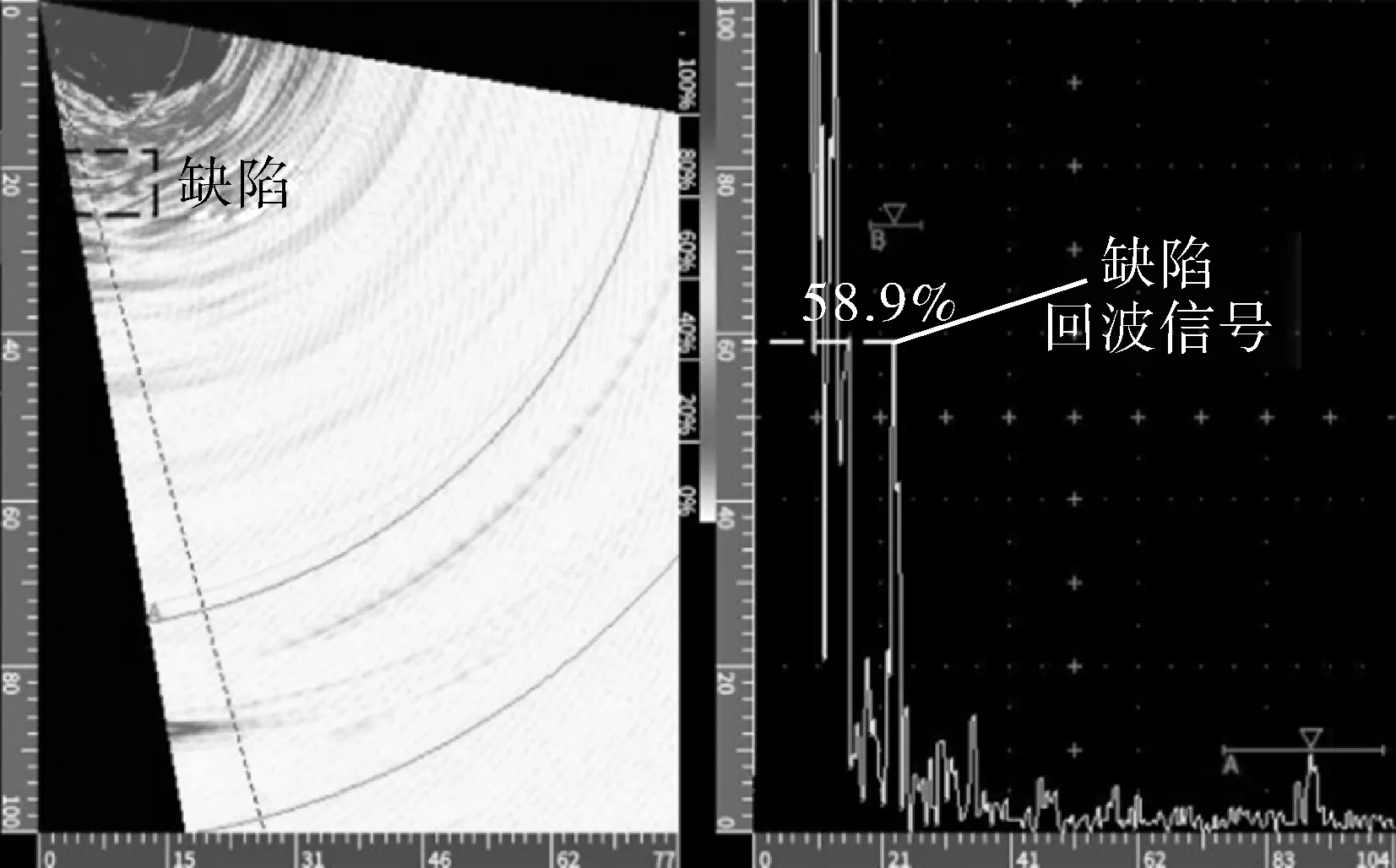
(c)通用的延时法则(缺陷回波信号)

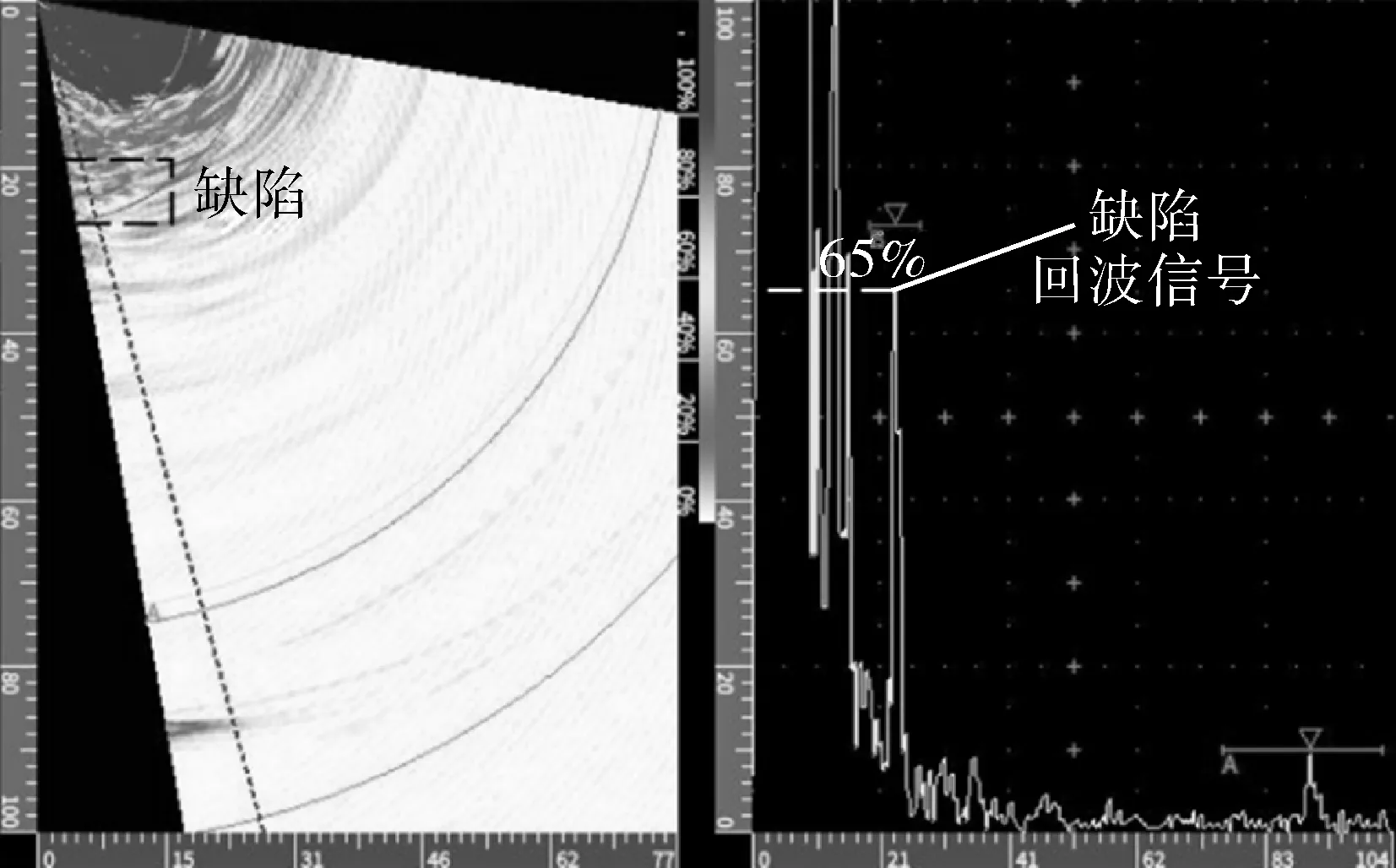
(d)改进的延时法则(缺陷回波信号)图9 改进的延时法则和通用的延时法则应用效果对比Fig.9 Comparison of application effects between improved delay rule and general delay rule

5 结语

(1)本文在理想波动声学方程的基础上，考虑声衰减和声频散的影响，提出了复合频率超声信号分解为多个单频信号的数值处理方法，计算并叠加各单频信号的传播规律，建立复合频率超声信号传播模型。

(2)结合实际检测结果，对比分析了不同频率组分的声衰减系数和相速度为变量、声衰减系数和相速度为常量两种情况下缺陷模拟结果的差异，结果表明，当模型考虑PE声衰减和声频散特性时，模拟结果与试验检测结果更接近，焦点所在深度的孔洞缺陷信号幅值偏差为11.77%。

(3)基于复合频率超声信号传播模型，考虑复合频率超声信号传播的群速度随检测深度变化规律，改进超声相控阵检测的延时聚焦法则，并将其应用于大壁厚PE管超声相控阵检测，检测结果表明，聚焦区域的内壁面回波信号增强了5.1%，非聚焦区域的缺陷信号增强6.1%。