基于状态重构器的顶驱控制方法

姜浩，牛学斌，张立军，尹文波，张丙辉，徐文凯

(1.中国石油大学(华东) 机电工程学院，山东青岛，266580；2.中石化胜利石油工程有限公司钻井工艺研究院，山东东营，257000)

钻柱的黏滑振动是井底钻头摩擦引起的一种“黏滞—滑脱—黏滞”的特殊转动形式。随着油气开发由浅层转向深层，钻井深度增加，钻柱的等效刚度降低，传递的扭矩不足以克服钻头和地层之间的摩擦力，从而产生黏滑振动，导致钻具的振动加剧，容易发生钻井事故，增加钻井成本[1]。

HONG 等[2]提出了利用Kalman 状态估算的方法计算井下钻头的位置与速度，利用数值方法分析控制性能，识别钻头的黏滑振动，估算钻头处的摩擦扭矩；黄根炉等[3-5]建立单自由度扭转模型，分析了大位移井钻柱黏滑振动机理，阐明了顶部转矩负反馈减振方法；汤历平等[6-7]建立了钻柱系统的黏滑振动力学模型，研究了黏滑振动的自激振动特性，分析了不同初始条件下钻头的相轨迹及钻头处所受的摩擦扭矩；NAVARRO-LOPEZ等[8]提出了动态滑模控制策略来控制钻柱系统的黏滑振动，结合相应参数，对比分析了不同控制方法的稳定性和鲁棒性；付蒙等[9-11]基于二自由度集中质量模型，建立了状态反馈和扭矩前馈振动控制方法。

我国对于钻柱黏滑振动研究相对国外起步较晚，对于减小钻头黏滑振动的控制算法研究较少。基于上述学者的研究成果，本文作者建立钻柱系统模型，分析黏滑振动特性，进行控制算法的仿真及实验研究，验证了井下参数重构算法的有效性，这对提高钻井效率减少事故发生具有重要意义。

1 数学模型建立

钻柱系统是整个钻井设备中的重要组成部分，图1所示为钻柱系统结构图，钻柱系统结构主要由4个部分即顶驱、钻杆、钻铤和钻头构成。

图1 钻柱系统结构图Fig.1 Structure diagram of drill string system

将顶驱，钻杆，钻铤和钻头视为等效的质量集中块，考虑到在实际的钻井工艺中，钻铤和钻头之间的刚性非常大，将钻铤和钻头视为一个等效集中质量刚体，将钻杆视为仅有扭转刚度而无惯性的弹簧，将钻井液对系统运动的影响视为黏滞阻尼，建立三集中质量钻柱系统运动模型[12]，如图2所示。

图2 钻柱系统运动模型Fig.2 Diagram of drill string system movement model

根据刚体运动学定律，分别对等效质量块进行运动学分析，顶驱运动方程如下：

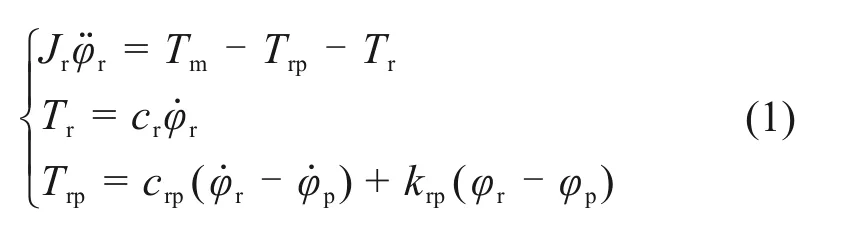
式中：Jr为顶驱的转动惯量；cr为顶驱的阻尼系数；φr为顶驱的旋转角位移；crp为顶驱和钻杆之间的等效阻尼系数；krp为顶驱和钻杆之间的等效扭转刚度系数；Tm为顶驱的驱动力矩；Trp为顶驱与钻杆之间的合力矩；Tr为顶驱的阻力矩。

中间钻杆等效质量刚体运动方程如下：

式中：Jp为钻杆的转动惯量；φp为钻杆的旋转角位移；φb为钻头处的旋转角位移；Tpb为钻杆与钻头之间的合力矩；cpb为钻杆和钻头之间的等效阻尼系数；kpb为钻杆和钻头之间的等效扭转刚度系数。

底部钻头等效质量刚体运动方程如下：

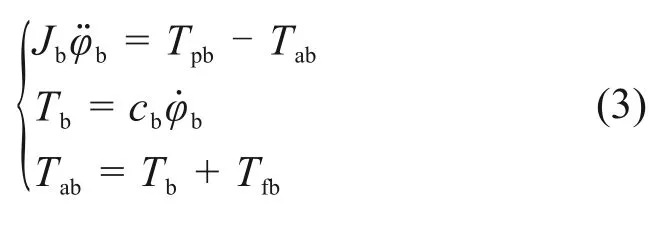
式中：Jb为钻头的转动惯量；cb为钻头的流体阻尼系数；Tab为钻头所受的合阻力矩；Tb为钻头的流体阻力矩；Tfb为钻头与地层之间的摩擦力矩。

综合式(1)～(3)可得三集中质量钻柱系统数学模型运动方程：

由黏滑振动引起Tfb属于非线性摩擦，其可采用Karnopp非线性摩擦模型进行分析。定义一个极小的速度极限Dv，当速度位于[-Dv，Dv]区间内，可认为速度v为0，此时，摩擦力是静摩擦力，它与系统所受其他合力相平衡，直到它超过最大静摩擦力时，系统进入滑动阶段，所受摩擦力与速度有关。Karnopp非线性摩擦模型表达式如下：

式中：v为系统运动速度；fs为最大静摩擦力；fe为外力合力；fc为库仑摩擦力；fv为摩擦黏性系数；vs与δ均为Karnopp摩擦模型经验常数[13]。

对式(4)所示钻柱运动数学模型选取状态变量：

式中：Δφrp=φr-φp；Δφpb=φp-φb。将式(4)写成状态空间方程：

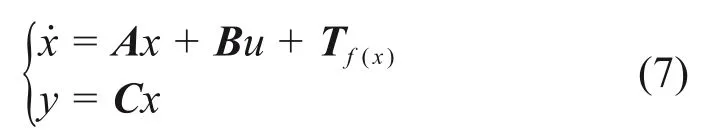
式中：A为系统的状态矩阵；B为系统的输入函数矩阵，u=Tm；C为系统的输出函数矩阵。各控制矩阵分别为：

2 控制方案设计

在实际钻井过程中，井下高压高温的工况条件及泥浆岩屑运移等导致难以直接获得井下数据，影响到井下工况的实时判断和对钻柱系统的实时控制，井下黏滑振动难以抑制。本文提出建立龙伯格状态重构器，依据地上顶驱转速ωr和扭矩Tm，估算钻柱系统进行控制所需要的井下状态变量[14]，设计了基于状态重构器的PID控制器。给定钻柱系统期望转速ωref，通过调节顶驱转速ωr和扭矩Tm，实现井下钻头实际转速ωb与期望转速ωref保持一致，完成钻柱系统黏滑振动的抑制，控制系统方案见图3。

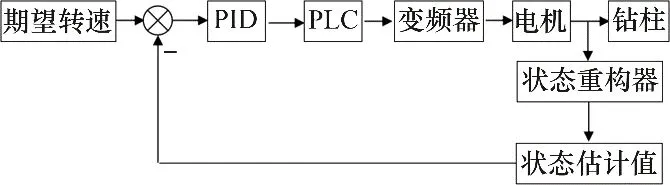
图3 控制系统方案图Fig.3 Scheme diagram of control system

2.1 状态重构器设计

式(7)所示的钻柱系统状态空间方程中x为5维空间状态变量，u为系统的输入量，y为系统的输出量，Tf(x)为摩擦干扰输入量，而A，B和C均为确定维数的系统矩阵。在通常情况下，式(7)对应的龙伯格状态重构器为

由于非线性摩擦干扰Tf(x)的存在，无法估算井下未知状态参量，故需对状态重构器进行修正，增加摩擦干扰估算项并通过估算值的误差积分[15]予以调整，调整后的龙伯格状态重构器[16]表示为

式中：为系统状态的估算值；为摩擦干扰输入估算值；Ga和Gb为相应的增益矩阵。根据系统的状态方程，以顶驱转速ωr和输入扭矩Tm为重构器输入量，以状态变量x和摩擦力矩Tf(x)为估算变量，进行如下代换：

将式(14)代入式(13)状态重构器，可得如下方程：

式中：G1，G2，G3，G4，G5和G6为增益比例系数。为了选定合适的增益比例系数，采用最优阻尼原理[17]确定参数。假设式(15)对应的状态矩阵为M，根据|sE-M|=0 可求出状态重构器的特征方程式(E为6 阶单位矩阵)。最优阻尼原理是将确定形式的控制器或者重构器和被控对象结合成整体系统，根据系统的传递函数整理成为最优阻尼特征多项式形式，从而得到与之相匹配的未知参数。式(15)对应的最优阻尼特征多项式为

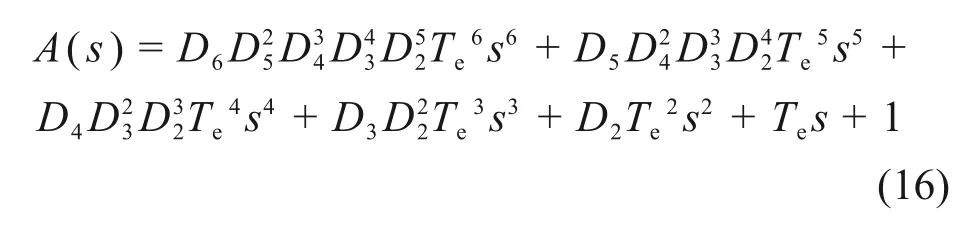
式中：D1，D2，D3，D4，D5和D6为系统阻尼比，根据最优阻尼原理，所有系统阻尼比均取0.5；Te是系统的时间常数，参考文献[18]，取0.3 s。通过将状态重构器的特征方程式化为6阶最优阻尼特征多项式的形式，对比参数方程组可获得比例增益系数G1，G2，G3，G4，G5和G6，经过计算可得比例增益系数分别为105.82，2.40×103，5.62×105，-7.31×104，1.25×107和-14.33，采用稳定判据分析可知状态重构器收敛、稳定。

2.2 PID控制器设计

根据式(15)可获得未知状态变量的估值，利用状态重构器与传统PID控制理论相结合，既增强了传统PID控制对非线性系统的抗干扰能力，又可根据状态重构器的估算数据为PID 算式提供校正信息。根据图3所示整体控制系统方案，采用MATLAB构建PID状态反馈控制器。PID控制系统的一般方程式如下：

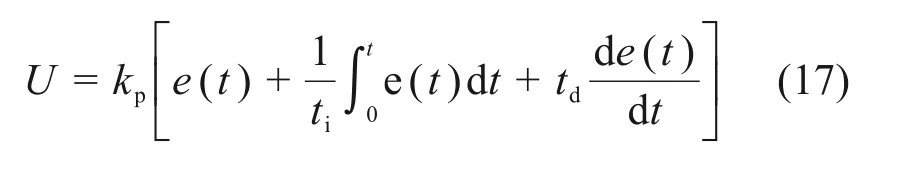
式中：kp，ti和td分别为比例系数、积分时间常数和微分时间常数。

PID控制系统通过调节井下转速和给定转速保持一致，从而消除钻柱的黏滑振动现象，故取e=ωref-ωb，其中，ωref为钻柱系统在输入驱动扭矩下的所期望的正常转速。由于井下转速未知，故取e=ωref-ωb_re，其中，ωb_re为钻头估算转速，从而得到关于输入扭矩Tm的控制方程式为

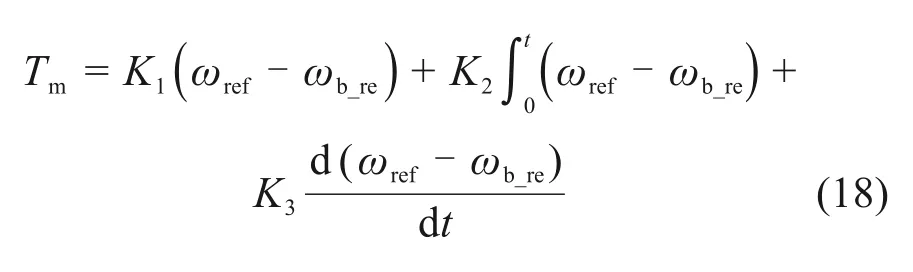
式中：K1，K2和K3分别为比例系数、积分系数和微分系数，经过调试，比例系数、积分系数和微分系数分别取14，32 和13。PID 控制器仿真模型见图4。

图4 PID控制器系统仿真模型Fig.4 Simulation model of PID controller system

3 仿真分析

为了验证控制方法对黏滑振动的抑制效果，搭建的三集中质量钻柱系统仿真模型和状态重构器仿真模型[19]见图5。仿真模型参数参考文献[20]，见表1。

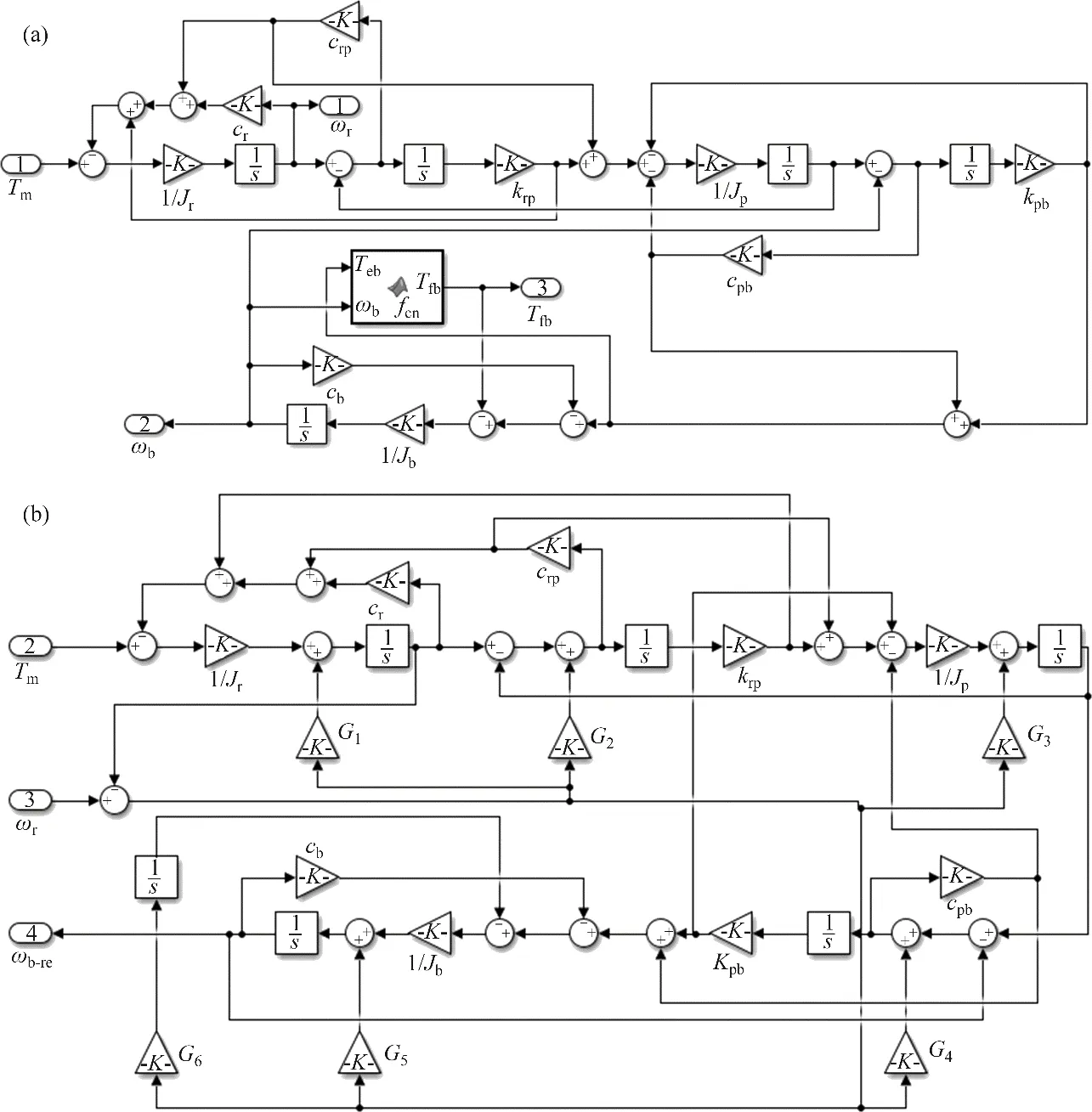
图5 钻柱系统和状态重构器仿真模型Fig.5 Simulation models of drill string and state reconstructor

在顶驱恒扭矩驱动模式下，可以得到不同顶驱驱动扭矩工况下顶驱转速ωr、钻头转速ωb以及摩擦力矩Tfb的时域分析图，根据表1给定的系统参数，设系统初始状态为0，获得的MATLAB/Simulink仿真结果见图6。

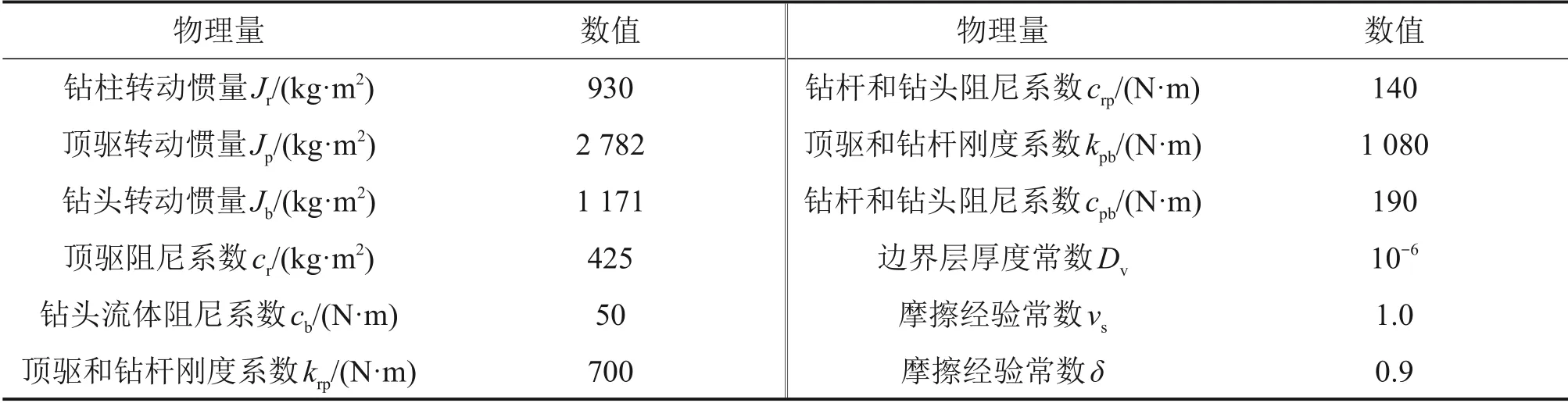
表1 钻柱系统数学模型参数Table 1 Related parameters of mathematical model of drill string system

由图6可知：当Tm为5 000 N·m 时，输入扭矩较小，顶驱传递到底部钻具的耦合力矩小于系统受到的静摩擦力矩，此时，驱动力矩不足以驱动井底钻具，ωb始终为0，ωr和Tfb经过短暂波动后保持不变，顶驱力矩与静摩擦力矩相互抵消，系统未出现黏滑振动现象；当Tm为10 000 N·m 时，钻柱系统出现明显的黏滑振动，井下钻具出现“黏滞—滑脱—黏滞”的周期性的交替运动，交替周期约为8 s，ωr波动范围为3～8 rad/s，而ωb波动范围在0～18 rad/s；底部受到的摩擦力矩Tfb也发生剧烈震荡，Tfb的波动范围为5 140～12 120 N·m，最大瞬时差值达6 976 N·m，Tfb的波动导致井下转速也出现巨大波动，ωb在极短时间内达到ωr的数倍；当Tm提升到15 000 N·m，起始状态顶驱转速和钻头钻速存在差异并呈现小幅波动，随着时间增加，系统黏滑振动逐渐消失，46 s后，ωr和ωb趋向稳定且两者数值相同，此时，井底钻具所受力矩为滑动摩擦力矩。

为模拟黏滑振动下状态重构器对状态变量的估算效果，根据图6所示仿真结果，取Tm=10 000 N·m，对状态重构器进行仿真验证，仿真参数同表2，仿真结果见图7。图7中,ωr_re和ωb_re分别为ωr和ωb的估算值。由图7可知：状态重构器对井下状态变量具有良好模拟性能，对ωr的估算误差趋近0。对于ωb的估算，在“黏滞”状态时存在较小估算误差，但在“滑脱”状态时其估算误差也趋近0，由此可知状态重构器可用于诊断黏滑振动的发生以及估算井下未知状态变量。

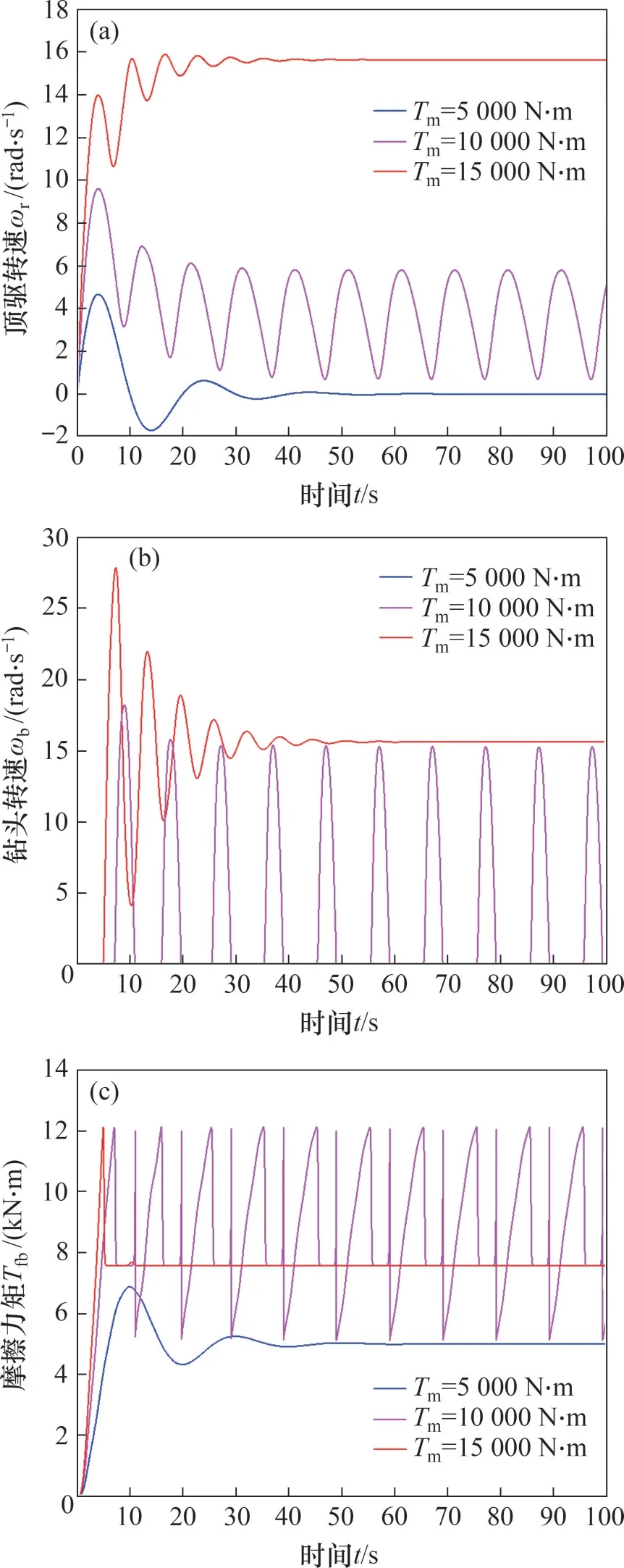
图6 不同扭矩下的转速和摩擦力矩时域分析图Fig.6 Time domain analysis diagrams of rotational speed and friction torque under different torques

图7 状态重构器效果时域分析图Fig.7 Time domain analysis diagrams of state reconstructor effect

为了不影响原有电控系统，采用PID控制系统对钻柱系统黏滑振动进行抑制，根据式(18)，在MATLAB/Simulink 中设定ωref为8 rad/s。为了对比PID控制系统对黏滑振动的抑制效果，在50 s处开启PID 控制，仿真结果见图8。由图8可知：未启动PID控制系统之前，钻柱系统持续性发生黏滑振动，50 s时开启PID控制系统，经过大约10 s抑制调整，井下钻具和顶驱转速ωr与ωb逐渐保持一致且与当前驱动扭矩下设定的稳态转速ωref一致。控制器在50 s 时进行控制切换，起始ωr与ωb会产生明显黏滞阶段，存在较大波动，在控制系统作用下，经过短时间超调后逐渐收敛至平稳。所设计的PID控制方法对黏滑振动具有良好控制作用。

图8 PID控制系统仿真时域分析图Fig.8 Time domain analysis diagram of PID control system simulation

4 实验验证

4.1 模拟试验台设计

为了进一步分析黏滑振动，验证控制方法对黏滑振动的控制效果，搭建了钻具黏滑模拟试验台，钻柱黏滑模拟实验装置原理图见图9。

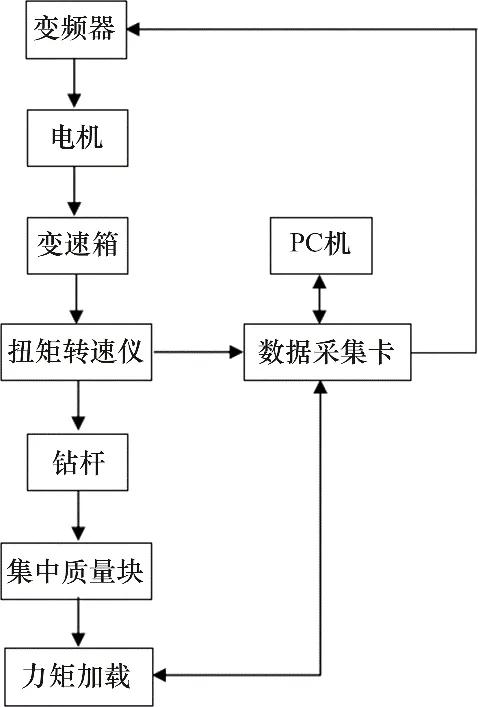
图9 实验装置原理图Fig.9 Schematic diagram of experimental device

试验台采用金属圆盘代表集中质量块，采用淬火钢杆连接件连接模拟钻杆与圆盘，电控系统驱动电机带动钻杆模拟装置转动，模拟钻进过程。试验台采用PCI数据采集卡采集驱动电机的实时转速和扭矩，将采集的转速和扭矩数据输入工控机，经控制算法处理后，输出控制信号控制电机转速，实现钻柱系统黏滑振动的抑制。

4.2 实验结果及分析

试验装置通过PID控制驱动变频器实现调速与扭矩输出，通过人机接口软件对试验装置的转速、输入扭矩、摩擦力矩等进行实时检测。为检验控制算法的控制效果及状态重构器的跟踪效果，分别将顶驱转速和钻头转速真实测量值与估算值进行实时对比，在模拟黏滑振动过程中启动控制器，获得的顶驱、钻头转速及重构器估算曲线见图10。

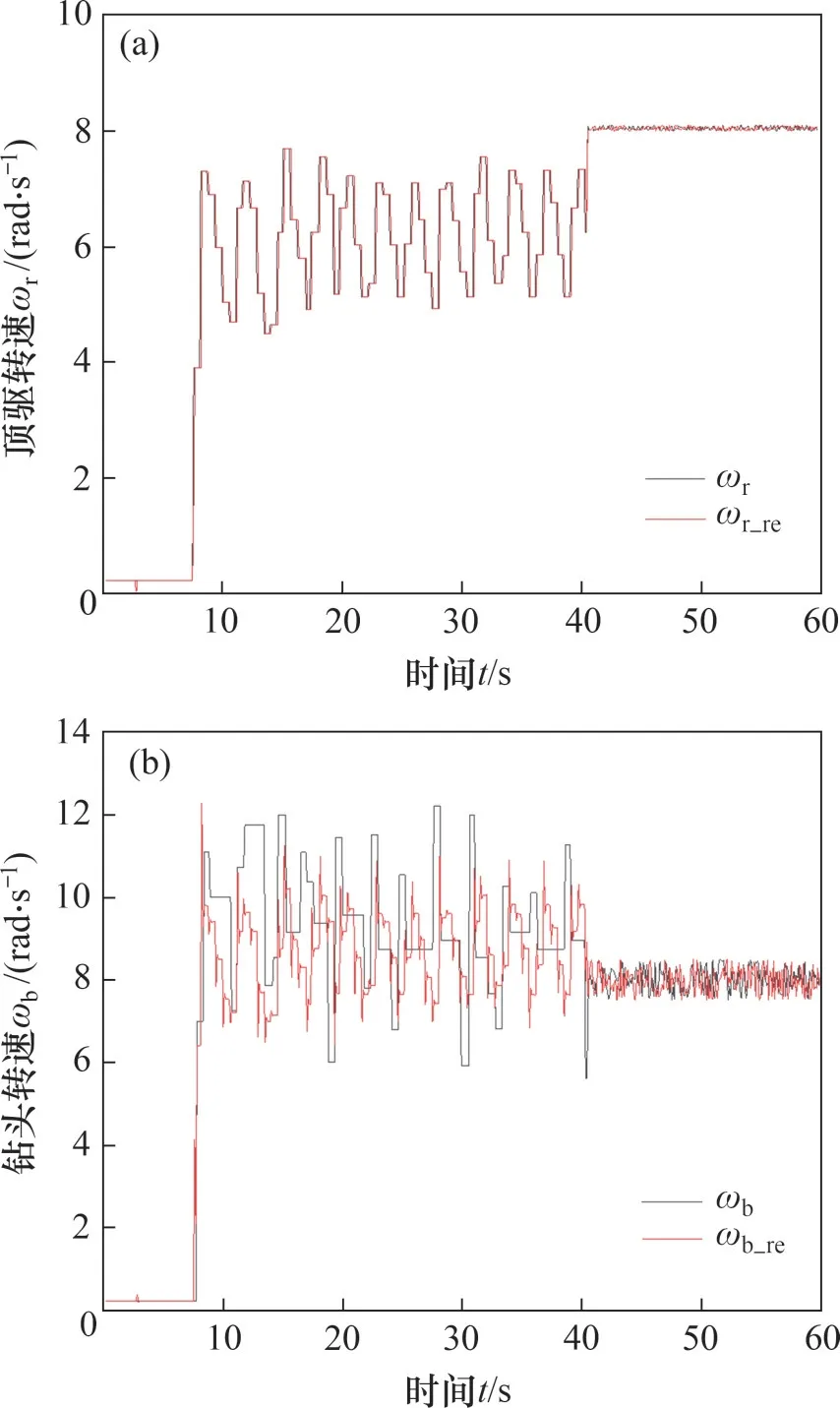
图10 试验台控制效果图Fig.10 Diagrams of experimental device control effect

黏滑振动模拟试验台启动后在7 s 时出现黏滑现象。从图10可以看出：未开启黏滑控制之前，系统出现明显的黏滑振动现象，顶部转速出现波动，底部转速振动程度相对较大；在40 s时开启黏滑控制算法，顶驱和钻头转速波动逐渐减小，转速趋于一致，保持在设定转速附近小幅度波动，黏滑振动控制性能如表2所示。

表2 黏滑振动控制性能Table 2 Control performance of stick-slip vibration

实验结果表明：黏滑抑制控制前后状态重构器对试验台顶驱转速估算相对误差均值分别为0.29%和0.01%，对钻头转速相对误差估算均值分别为7.0%和3.07%，当钻柱系统产生黏滑振动时，控制算法能够有效控制电机的转速。试验台模拟钻进时，由于模拟钻杆和台架支撑套之间不可避免地存在摩擦，测量仪表及加载装置也存在测量误差，故施加黏滑抑制控制后钻头钻速存在小幅波动，但在较大程度上抑制了井下黏滑振动，实验结果验证了控制算法的有效性。

5 结论

1)基于非线性摩擦理论，建立了三集中质量钻柱系统运动方程，采用最优阻尼参数，提出了基于龙伯格状态重构器的顶驱黏滑抑制控制算法。

2)设计了基于状态重构器的PID 控制算法，通过状态重构器对顶驱钻速和井下钻头转速进行估算，实现了闭环控制，解决了井下参数无法获取的难题。

3)设计的基于状态重构器的反馈控制算法可在10 s内完成黏滑振动的控制。

4)状态重构器对试验台钻头转速估算准确，控制算法对井下钻头黏滑振动有较好的抑制作用。