含水合物沉积物孔隙流动特性数值模拟

张吉东，刘晓惠，边培明，吴强，殷振元

(1.清华大学清华大学深圳国际研究生院，广东深圳，518055；2.山东科技大学能源与矿业工程学院，山东青岛，266590；3.深圳市百勤石油技术有限公司，广东深圳，518055；4.黑龙江科技大学安全工程学院，黑龙江哈尔滨，150022)

天然气水合物广泛分布于海底的沉积物层及永久冻土层中，储量丰富且具有高能量储存能力，燃烧时只释放CO2和H2O，是未来清洁能源的重要组成部分[1]。目前，中国[2]、日本[3]等国家均对天然气水合物进行了试采工作，但由于储层力学性质及其流动的复杂性，天然气水合物的商业化开采仍是世界性难题。在含水合物沉积物中，渗透率是流体流动性能的关键指标，决定了水合物的生长、分布及甲烷气体的开采效率。为此，了解流体在孔隙中的渗透特性对于准确预测产液行为至关重要。考虑到通过室内物理实验确定渗透率特性影响因素需要复杂的测试设备和精确控制的环境[4]，本文基于数值模拟手段研究含水合物沉积物储层的流动特性。

沉积物孔隙结构是控制渗透率演化规律的首要因素，而孔隙结构变化则受多种因素的影响，孔隙内固相水合物生成和分解是影响孔隙结构的重要因素。目前，学者们普遍将沉积物中的水合物的微观结构分为表层覆盖、颗粒胶结与孔隙填充等形态[5]；同时，伴随着水合物饱和度增加，水合物形态通常从表层覆盖与孔隙填充型逐渐向颗粒胶结型转化[6-7]。沉积物粒径是影响渗透率演化的另一因素，宋永臣等[8-9]开展的沉积物渗透率实验结果表明，沉积物的绝对渗透率随粒径增大而升高，但由于实验沉积物砂粒种类较少，并未全面分析黏土至粗砂多粒径范围内渗透率变化的差异。LIU等[10]发现南海神狐海域含甲烷水合物沉积物属于泥质细粉砂型储层。当前对真实储层粒径分布的含水合物非均质沉积物储层的渗透率演化规律研究较少，因此，有必要利用数值方法深入分析粒径导致的渗透率变化。张永超等[11]基于核磁共振(NMR)结果，发现水合物主要存在于孔径较大的孔隙中，水合物的生成具有明显的非均质性；蒋观利等[12]基于CT 实验，发现甲烷水合物生成早期结构非常疏松，呈絮状，后期逐渐密实；李晨安等[13]通过以Al2O3球为多孔介质的CT 扫描实验，发现水合物生成早期主要位于气-水界面，孔隙内水合物密度较低，随着水合物饱和度增加，多孔介质孔隙结构完全被水合物占据，整个生成过程中存在明显的非均质性分布。结合上述分析，当前人工合成的沉积物储层砂质颗粒粒径通常较单一，无法有效呈现真实含水合物沉积物粒径范围广、差异大的特点；同时，当前砂质颗粒空间非均质性对渗透率演化规律影响的研究较少，非均质性对渗透率变化的机理仍不明确。为此，本文在孔隙尺度探究水合物饱和度、砂质颗粒粒径和砂质颗粒空间非均质性3种因素对渗透率演化规律的影响。

当前格子玻尔兹曼方法(LBM)、孔隙网络模型(PNM)和有限单元法(FEM)是研究水合物生成过程中的渗透率演化规律中常用的方法。HOU 等[14]基于LBM 方法从水合物饱和度、矿物颗粒排列、水合物生长及分布形态等方面分析了水合物对多孔介质渗透率变化的影响；ZHANG等[15]基于LBM方法建立了考虑分解动力学、气体流动和传热机理的孔隙尺度框架模型，研究了甲烷水合物分解过程中非等温多重物理化学过程。但LBM 方法无法表征砂粒粒径，并不能有效分析粒径因素对渗透率演化规律的影响。MAHABADI 等[16]建立了孔隙网络模型，模拟在初始饱和度为10.0%～60.0%时的水合物分解，计算相对水渗透率和相对气渗透率，并修正了STONE方程的拟合参数。虽然PNM方法可以很好地描述多孔介质宏观尺度属性，但由于简化了多孔介质，因此丢失了一些水合物分布形态的信息。由于上述2种方法并不能有效研究砂质颗粒粒径及水合物形貌对含水合物沉积物渗透率变化的影响，而基于有限单元法的COMSOL Multiphysics 在含水合物沉积物砂质颗粒和水合物形貌构建方面更为有效，本文采用基于有限单元法的COMSOL Multiphysics模拟器，求解含水合物沉积物渗透率演化。

本文重点讨论砂质颗粒粒径、水合物饱和度和砂质颗粒空间非均质性对含水合物沉积物渗透率的影响。首先，采用基于有限单元法的COMSOL Multiphysics分析上述因素对渗透率演化规律的影响，其中，非均质几何模型颗粒及位置遵循正态分布并通过MATLAB 程序生成；其次，为验证模型的正确性，将数值模拟结果与实验数据进行对比分析，并通过修正Tokyo模型对本文数值模拟结果进行拟合，分析均质模型与非均质模型下修正Tokyo模型参数的差异。

1 几何模型及计算方法

1.1 砂质颗粒粒径划分

为研究砂质颗粒粒径对水合物沉积物渗透率的影响，参考文献[17]，将几何模型颗粒划分为4种不同范围的粒径尺寸，并选择范围上限作为模拟粒径，如表1所示。

表1 砂质颗粒粒径划分[17]Table 1 Sand particle size classification[17]

1.2 含水合物沉积物几何模型

在含水合物沉积物储层中，天然气水合物呈现3种不同的形态：表层覆盖、孔隙填充和颗粒胶结。图1所示为含水合物沉积物CT 图像。由图1(c)和(d)可见，表层覆盖水合物通常在实验前期即在孔隙中生成；由图1(b)可知孔隙填充和颗粒胶结水合物主要在实验中后期被观察到，且为水合物存储的主要形态。本文主要研究孔隙填充型水合物的生成对渗透率演化规律的影响，同时，数值模拟均以球形表征沉积物固体颗粒和孔隙填充型水合物形状。在模型中，将砂质颗粒包裹，且将未被水合物填充的空间定义为孔隙，砂质颗粒间相互连通相对狭窄的空间定义为孔喉。

图1 含水合物沉积物CT图像[18]Fig.1 CT images of hydrate-bearing sediments[18]

为探究砂质颗粒空间非均质性对渗透率演化规律的影响，分别建立均质几何模型与非均质几何模型，如图2所示。由图2(a)可见：砂质颗粒(深灰色)与水合物(红色)均匀分布，砂质颗粒间距ds=a×D50/2，其中a为砂质颗粒粒径与颗粒间距的比。由于模型砂质颗粒及水合物几何关系的限制，当球形水合物直径与砂质颗粒间距相等时，水合物饱和度达到最大值，但由于孔隙未被完全填充及孔喉部分无水合物的原因，本文水合物饱和度SH最大值为50.0%。由图2(b)可见：沉积物中D50=125.0 μm颗粒(深灰色)体积占全部颗粒的体积分数为70.0%，D50=62.5 μm颗粒(浅灰色)体积占全部颗粒体积的30.0%，D50=5.0 μm 水合物(红色)体积占孔隙体积定义为饱和度SH，2种砂质颗粒粒径及水合物尺寸均遵循正态分布，位置则是在保证互不重叠基础上的随机分布；非均质几何模型初始孔隙度φ及边界长度L与D50=125.0 μm 的均质几何模型的一致：φ=35.0%，L=0.89 mm，W=0.38 mm。

图2 基于CT图像重构的空间均质与非均质几何模型(孔隙填充型)Fig.2 Constructed homogeneous and heterogeneous geometric models(pore-filling type)

1.3 计算方法

本文模型采用二维模型，其中几何模型面积S1表示为

式中：L和W分别为模型的长度和宽度，μm；nx和ny分别为几何模型x和y方向的颗粒数目；D50为砂质颗粒直径，μm；ds为砂质颗粒间距，μm。

沉积物颗粒面积S2及水合物面积S3均基于COMSOL Multiphysics中的域积分求得，因此，含水合物几何模型初始孔隙度φ0及饱和度SH分别表示为：

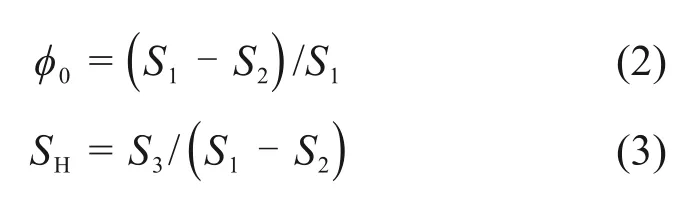
数值模拟中将含水合物沉积物砂质颗粒、水合物颗粒表面及模型上下边界均设置为无滑移边界，即|u|= 0。同时在模型的左边界设置入口压力Pu；右边界设置出口压力Pd。模型中的流动区域基于网格划分中的边界层来划分，模型网格采用超细化单元，模型边界条件及网格示意如图2(a)所示。在上述模型中，进行如下假设：

1)流体为不可压缩流体；

2)流体流动是由压差驱动的单相流动；

3)忽略重力的影响。

根据达西定律，COMSOL Multiphysics计算流体渗透率的表达式为：

式中：k为渗透率，m2；μ为黏度，Pa·s；Qg为气体流量，m3/s；A为样品横截面积，m2；Pu和Pd分别为上游压力和下游压力，Pa。为确保几何模型流体流态为层流，数值模拟采用的上下游压差为500.0 Pa，雷诺数Re为1.27。同时，流速u=Qg/A，表示为几何模型出口端的平均速度。数值模型输入参数及数值模拟的计算流程分别如表2和图3所示。

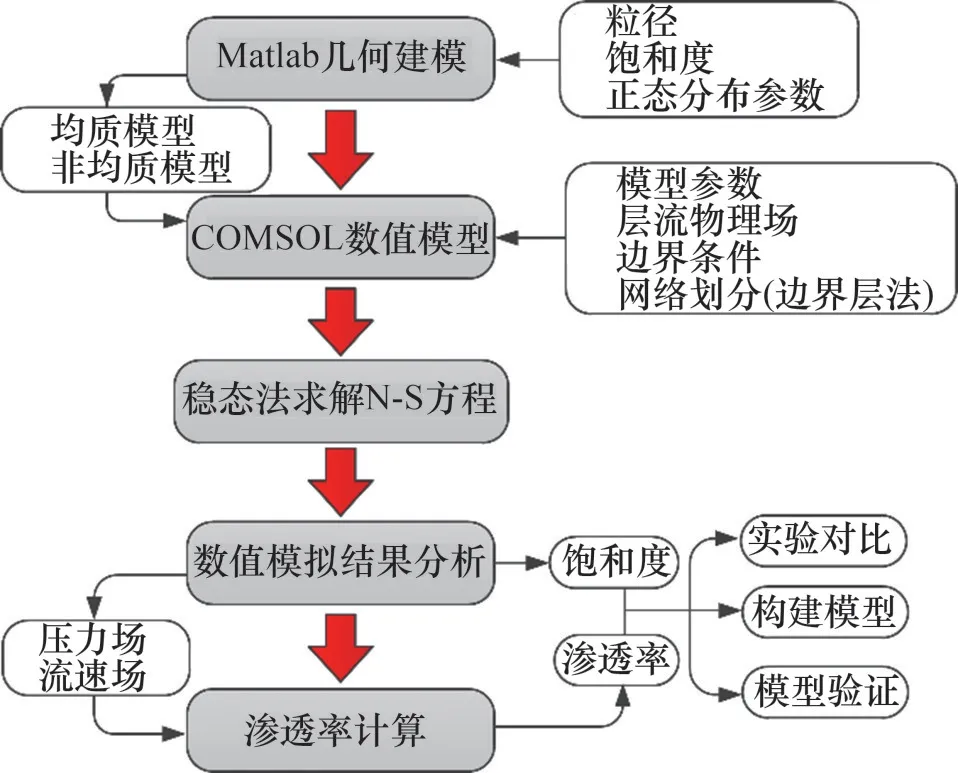
图3 数值模拟计算流程Fig.3 Flow chart of numerical modelling process

表2 数值模拟参数Table 2 Parameters of numerical simulation

2 含水合物沉积物渗透率的影响因素

基于建立的几何模型与数值模拟计算流程，探究砂质颗粒粒径、水合物饱和度及砂质颗粒空间非均质性3种因素对含水合物沉积物渗透率演化的影响。

2.1 砂质颗粒粒径

不同粒径下含水合物沉积物绝对渗透率与饱和度的关系如图4(a)所示。由图4(a)可见：在无水合物情况下，黏土颗粒至中砂颗粒4种沉积物绝对渗透率分别为1.06×10-16，1.04×10-13，1.65×10-12和6.41×10-12m2，颗粒粒径对渗透率变化影响显著，中砂型(D50=500.0 μm)水合物沉积物绝对渗透率是黏土型(D50=2.0 μm)沉积物的6×104倍；为量化粒径对渗透率的影响，将饱和度SH=41.1%时的各粒径含水合物沉积物绝对渗透率与相对渗透率进行对比分析，如图4(b)所示。由图4(b)可见：在一定饱和度下，随着沉积物颗粒粒径增长，沉积物绝对渗透率呈非线性上升趋势，不同粒径间的相对渗透率差异很小；其中粉砂型(D50=62.5 μm)沉积物渗透率至中砂型(D50=500.0 μm)沉积物绝对渗透率以3.0～4.0 倍的增长率逐渐上升，而黏土型(D50=2.0 μm)与粉砂型(D50=62.5 μm)沉积物绝对渗透率则相差962 倍，D50=62.5 μm 时相邻粒径渗透率变化加剧，因此，粉砂(D50=62.5 μm)为影响渗透率变化速率的拐点粒径。

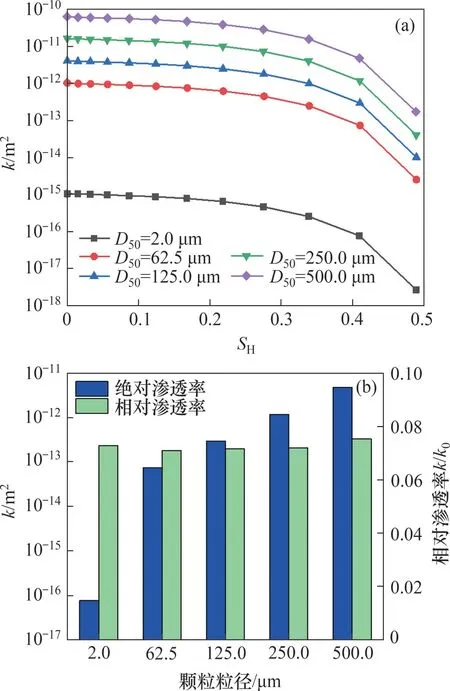
图4 颗粒粒径对水合物沉积物渗透率演化规律的影响Fig.4 Effect of particle size on permeability of hydratebearing sediments

上述结果表明，沉积物中的黏土体积分数对水合物储层的渗透率有较大影响，储层黏土体积分数将会直接影响到水合物开采的效率。根据文献[19]，我国南海神狐海域某区块沉积物颗粒属于泥质粉砂型[20]。

2.2 水合物饱和度

为量化研究饱和度对渗透率的影响，以各粒径无水合物时的渗透率作为初始渗透率，对不同粒径下的渗透率进行归一化处理，如图5所示，由图5可见：相对渗透率均随饱和度呈非线性下降的趋势；随着粒径增加，不同饱和度间的渗透率差异不大，这也许是均质模型本身的局限性(如随饱和度增加，迂曲度变化较小等)导致的，同时，本文模拟结果与XU 等[21]的模拟结果一致。从图5可以看出：随着饱和度增加，渗透率间的差异逐渐增大；当饱和度介于0～33.9%时，含水合物沉积物渗透率随饱和度呈线性降低近1个数量级，而当饱和度高于33.9%时，含水合物沉积物渗透率则呈指数快速下降近3个数量级。因此，SH=33.9%为饱和度对渗透率影响的拐点，当饱和度高于此拐点时，含水合物沉积物渗透率将快速下降。

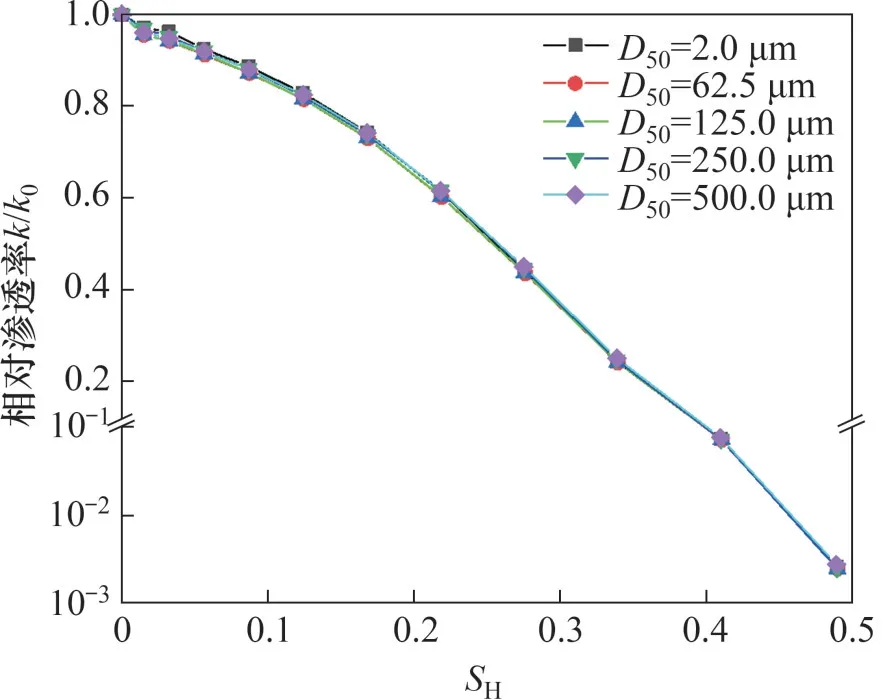
图5 饱和度对水合物沉积物渗透率演化规律的影响Fig.5 Effect of hydrate saturation on permeability of hydrate-bearing sediments

为探究饱和度对渗透率的影响，绘制不同饱和度下几何模型的流速场，如图6所示。由图6可见：随着水合物饱和度逐渐增加，沉积物颗粒与水合物间通道逐渐变窄；当饱和度从12.5%增至41.1%时，沉积物颗粒与水合物间孔喉半径R1与沉积物颗粒间孔喉半径R2的比(Rr=R1/R2)从1.64 降至0.35，含水合物沉积物流动通道堵塞并生成新的孔喉通道，致使沉积物孔隙通道流速降低。随着饱和度逐渐增加，两孔喉流速的比值(vr=v1/v2)从0.64(SH=12.5%)升至3.12(SH=41.1%)，孔喉半径R1逐渐成为流速控制的孔隙通道，这种流速与孔喉呈非线性下降趋势，导致饱和度SH高于33.9%时，沉积物渗透率急剧下降。

图6 不同水合物饱和度下孔喉及孔喉流速场演化规律Fig.6 Evolution of pore throat and associated flow field against hydrate saturation

基于上述现象，我们推断在水合物沉积物生成过程中，若前期表层覆盖型水合物率先生成，孔喉通道被迅速堵塞。储层渗透率将快速下降，导致生成水合物饱和度较低。而当孔隙填充型水合物占主导地位时，储层渗透率下降较慢，储层水合物饱和度较高；最后，当孔隙填充型水合物逐渐生长而与颗粒间生成新的孔喉时，渗透率将进一步降低。因此，含水合物沉积物储层渗透率的演化规律与水合物生长模式密切相关。

2.3 砂质颗粒空间非均质性

基于图1(a)的CT 图像可以看出，储层颗粒及水合物粒径及位置均为随机分布。为更加准确地描述水合物生成过程中储层渗透率的演化规律，以D50=125.0 μm 的颗粒体积分数为70.0%，D50=62.5 μm 的颗粒体积分数为30.0%组成非均质几何模型，并将其与D50=125.0 μm的均质几何模型进行对比分析，探究储层颗粒、水合物分布非均质性对渗透率演化的影响，其中，均质几何模型初始渗透率k0=3.96×10-12m2，非均质几何模型初始渗透率k0=1.35×10-12m2，2 种模型的相对渗透率结果如图7所示。

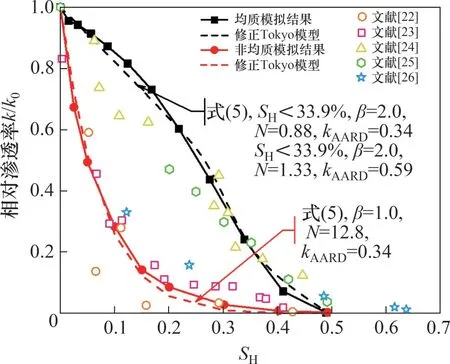
图7 水合物沉积物(空间均质与非均质分布)渗透率随饱和度演化规律及模型验证Fig.7 Relationship between relative permeability of hydrate-bearing sediments with hydrate saturation and model validation

从图7可以看出：2 种模型的渗透率变化速率有很大差异，非均质模型在随饱和度增加过程中变化速率逐渐减小，当SH=20.0%时，相对渗透率已有一个数量级的变化；均质模型渗透率变化速率则随饱和度增加逐渐增大，当SH=38.1%时，相对渗透率降低1个数量级。上述结果表明：非均质性会显著降低初始渗透率且渗透率对饱和度变化更加敏感。同时，将MINGAWA 等[22]、LIANG等[23]、DELLI等[24]、KUMAR等[25]、LEI等[26]的实验数据与数值模拟结果进行对比，发现相对渗透率实验数据位于2条曲线之间，其中，均质模型曲线为上边界，非均质模型曲线为下边界。

本文中，由于均质几何模型最大饱和度有一定适用范围(SHmax=50.0%)，根据图6所示流速场可以看出，当SH=41.1%时，流动通道几乎被完全堵塞，而孔隙内仍有部分空间未填充水合物；同时，其他学者实验数据中水合物最大饱和度约为60.0%[25]。因此，对Tokyo 模型中SH项添加系数β来量化实际饱和度与理想化SH=100.0%间的差异，修正后的模型表示为

采用绝对平均相差偏差kAARD评价修正的Tokyo模型与数值模拟拟合相对渗透率(k/k0)的效果，kAARD表示为

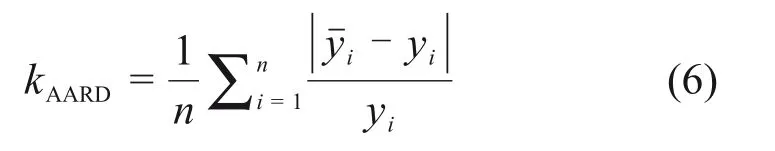
式中：为修正Tokyo 模型计算值；yi为数值模拟计算值。

在均质模型中，随水合物饱和度增加，当饱和度高于33.9%时含水合物沉积物绝对渗透率有突变的现象，如图5所示。为此，以SH=33.9%为分界点，利用式(5)进行分段拟合。由于水合物分布形态的差异，非均质模型中并未出现渗透率突变的现象，为此，非均质模型曲线未进行分段拟合，2 个模型的拟合结果如图7所示，均质与非均质Tokyo模型参数如表3所示。

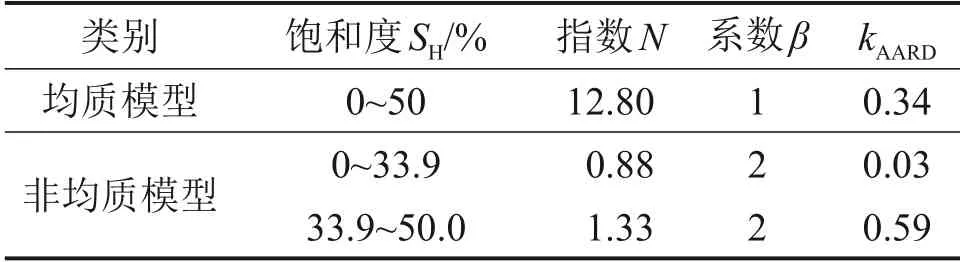
表3 修正的Tokyo模型拟合参数Table 3 Fitting parameters of corrected Tokyo models

由于非均质模型中孔隙填充水合物粒径仅5 μm，且位置随机分布，无限定饱和度适用范围，Tokyo模型拟合效果良好，而均质模型由于几何模型最大饱和度有一定适用范围，设定β=2的修正模型拟合效果更好。当考虑水合物在孔喉处生长时应适当增加N，但原因仍不明确。在本文中，非均质模型中N高于均质模型，因此，除水合物在孔喉处生长外，N升高与模型的非均质性有关。

3 结论

1)含水合物沉积物颗粒粒径是影响渗透率演化的重要因素，中砂型(D50=500.0 μm)与黏土型(D50=2.0 μm)沉积物绝对渗透率相差5 个数量级；在一定饱和度下，沉积物绝对渗透率随砂质颗粒粒径增大呈非线性上升趋势，且不同粒径间的相对渗透率差异很小；砂质颗粒粒径下降至拐点(D50=62.5 μm)后，绝对渗透率急剧下降，粉砂水合物沉积物绝对渗透率是黏土水合物沉积物的962倍(SH=41.1%)，储层黏土体积分数将会直接影响到水合物开采的效率。

2)含水合物沉积物相对渗透率均随饱和度呈非线性下降的趋势，储层流动通道逐渐变窄，两孔喉流速比vr与孔喉半径比Rr呈非线性下降的趋势，SH=33.9%为饱和度对渗透率影响的拐点，当饱和度高于此拐点时，含水合物沉积物渗透率快速下降。

3)模型非均质性会显著降低渗透率且渗透率变化对饱和度更加敏感，非均质模型中修正Tokyo模型的指数N比均质模型的大，N升高与非均质性有关；现有的相对渗透率实验数据通常位于2条曲线之间，其中均质模型曲线为上边界，非均质模型曲线为下边界。

4)由于实验测试结果间相差较大，后续将进行实验探究，进一步分析均质几何模型与非均质几何模型的差异。