基于有限元和数据重构的连续梁移动荷载识别研究

胡 烁， 任剑莹,2， 张 宇,2， 李俊良

(1.石家庄铁道大学 工程力学系，河北 石家庄 050043；2.石家庄铁道大学 省部共建交通结构力学行为与系统安全国家重点实验室，河北 石家庄 050043；3.石家庄铁道大学 工程训练中心，河北 石家庄 050043)

胡烁，任剑莹，张宇，等.基于有限元和数据重构的连续梁移动荷载识别研究[J].石家庄铁道大学学报(自然科学版),2022,35(1):7-12,91.

0 引言

移动车辆荷载的准确识别是桥梁结构健康监测与安全评估的重要内容，也是发现超载车辆的重要方法，对保障公路桥梁的安全运营具有重要的意义。O’Connor et al[1]提出了可以得到荷载时间历程的识别方法——解析法Ⅰ;Law et al[2]在时域内采用卷积方法对移动荷载进行了识别;Chan et al[3]使用了梁的欧拉方程模拟桥面，进而对移动荷载进行识别;卜建清等[4]采用广义正交函数对桥梁应变进行拟合，利用正则化技术得到识别结果;赵煜等[5]基于反向传播神经网络方法，分析了输入参数对荷载识别精度的影响。移动荷载识别主要是通过模态叠加法[2, 3, 6, 7]或有限元法[1, 8-10]，得到系统的振动方程，采用不同的逆求解方法，识别出移动荷载。连续梁桥[11]的移动荷载识别大多采用模态叠加法，而采用有限元法进行移动荷载识别的研究相对较少，因此，本文采用有限元法对连续梁桥进行移动荷载识别研究，并分析荷载移动速度、切比雪夫多项式项数、荷载大小和连续梁跨数等对移动荷载识别结果的影响。

图1 两跨连续梁计算模型

1 连续梁在移动荷载作用下的动力响应

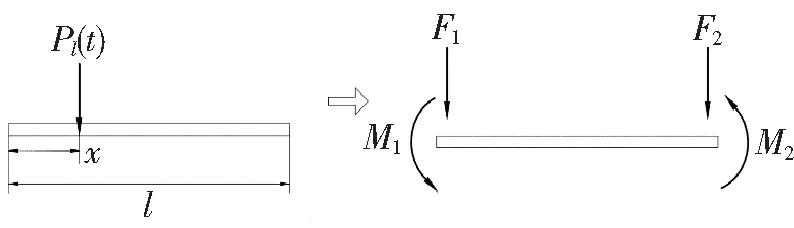
图2 等效节点荷载模型

图1所示为2个间距不变的移动力P1(t)和P2(t)，从左向右以速度v在一座两跨连续梁上匀速移动时，连续梁计算模型示意图。L为桥梁总长，x1(t)、x2(t)分别表示P1(t)、P2(t)的作用位置，a为P1(t)和P2(t)的间距。桥梁为等截面直梁(不考虑轴向变形的影响)，将桥梁离散为m个单元，共有m+1个节点。

图2为将作用在第j个梁单元上任意位置的荷载，等效为节点荷载的模型。l为单元长度，x为载荷位置，关系式

(1)

式中，Pl(t)(l=1,2)为移动荷载；l为连单元的长度；F1、M1、F2和M2为等效节点荷载；Hj为第j个梁单元的形函数，表示为

(2)

桥梁的运动方程表示为

(3)

最后，采用Newmark直接积分法求解式(3)得到桥梁的位移响应。

对于复杂连续梁桥在移动车辆荷载作用下的动力响应[12-13]计算，也可以采用有限元软件建模计算。为了便于分析，基于上述有限元理论，编制了连续梁在2个移动荷载P1(t)、P2(t)作用下动力响应的计算程序。

2 移动荷载识别方法

由于在实际工程应用中，同时测量位移、速度和加速度响应，费时费力，且误差较大，因此仅采用位移响应来进行移动荷载的识别。

基于式(3)计算或测得桥梁位移响应，采用切比雪夫多项式[14]拟合位移响应函数和曲线

(4)

式中，Ti(t)为切比雪夫正交多项式；Nf为切比雪夫正交多项式的项数，需小于位移响应的数据量；Ci(x)为展开式中的系数；R1为拟合后的桥梁位移响应。

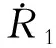
(5)

(6)

(7)

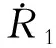
U=HCP识别

(8)

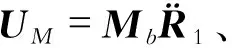
(9)

为了求解式(9)，引入Tikhonov泛函

Fδ(x)=‖HCP识别-U‖2+λ‖P识别‖2

(10)

由L-曲线方法和广义交叉检验[8]可以确定参数λ。

采用最小二乘法求解式(10)得到移动荷载

(11)

式中，I为单位矩阵。

3 数值模拟

3.1 桥梁动力响应

以河北省境内跨冶河的某连续梁桥为例进行数值模拟计算。其中，桥梁参数见表1。

表1 连续梁桥参数

移动荷载采用文献[8]中的2个间距不变的时变集中力

(12)

根据式(11)计算得到识别结果，计算荷载识别的相对误差(relative percentage error，简称RPE)

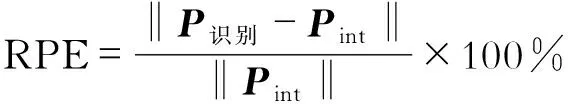
(13)

式中，‖·‖为矩阵范数；P识别为识别结果。

当Pint以15 m/s的速度在连续梁上移动时，计算得到该两跨连续梁各节点的位移响应，图3(a)为第一跨(图1中左边跨为第一跨)跨中的竖向位移时程曲线计算值和采用切比雪夫多项式拟合重构数据的对比图，图3(b)、图3(c)分别为第一跨跨中速度和加速度的计算值和采用Newmark方法得到的重构数据的对比图。计算相对误差(RPE)

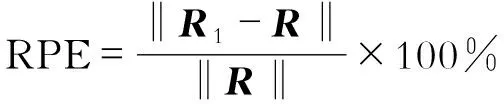
(14)

式中，‖·‖为矩阵范数;R1、R分别为重构结果、实际结果。

图3 两跨连续梁第一跨跨中位移、速度、加速度响应计算值与重构值对比图

图4为切比雪夫多项式的项数对位移、速度和加速度重构的相对误差的影响情况。

图4 多项式项数对两跨连续梁第一跨跨中位移、速度、加速度拟合误差的影响

由图3、图4可以看出位移、速度、加速度的拟合曲线与计算曲线吻合较好，相对误差都是随着项数的增加而变小，位移的拟合效果最好，相对误差都在1%以下。当切比雪夫多项式达到500项时，位移、速度和加速度的拟合误差分别为0.001 6%、0.095%和2.28%，且项数大于500后，位移、速度和加速度的拟合误差保持稳定且很小，为了提高计算效率，选择500项切比雪夫多项式进行位移响应的拟合。

3.2 荷载识别

位移、速度、加速度重构后，由式(11)进行荷载识别。图5、图6分别为2个移动荷载的识别结果Pi1、Pi2。

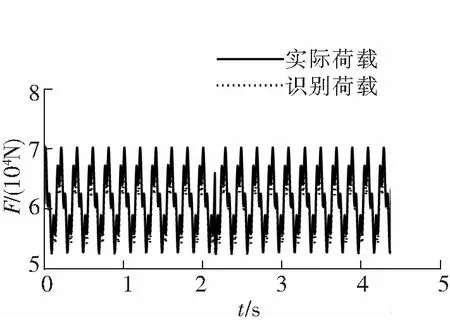
图5 两跨连续梁识别结果Pi1

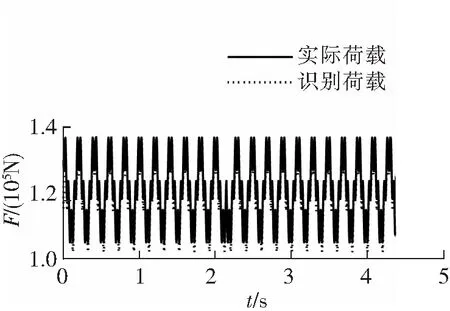
图6 两跨连续梁识别结果Pi2

由图5、图6可以看出，识别荷载与实际荷载很接近。Pi1、Pi2的相对误差分别为1.94%、5.40%，相对误差都在10%以内。

4 荷载识别的影响因素

4.1 位移、速度和加速度对荷载识别结果的影响程度分析

由式(9)可知，荷载识别是通过位移、速度和加速度三者对应的弹性力、阻尼力和惯性力叠加后，进行荷载识别的。下面分析三者对移动荷载识别结果的影响程度。分别将弹性力UK、阻尼力UC和惯性力UM单独代入式(11)中，得到分别仅由弹性力、阻尼力和惯性力识别的移动荷载PK、PC和PM。图7为识别荷载与实际荷载对比图。

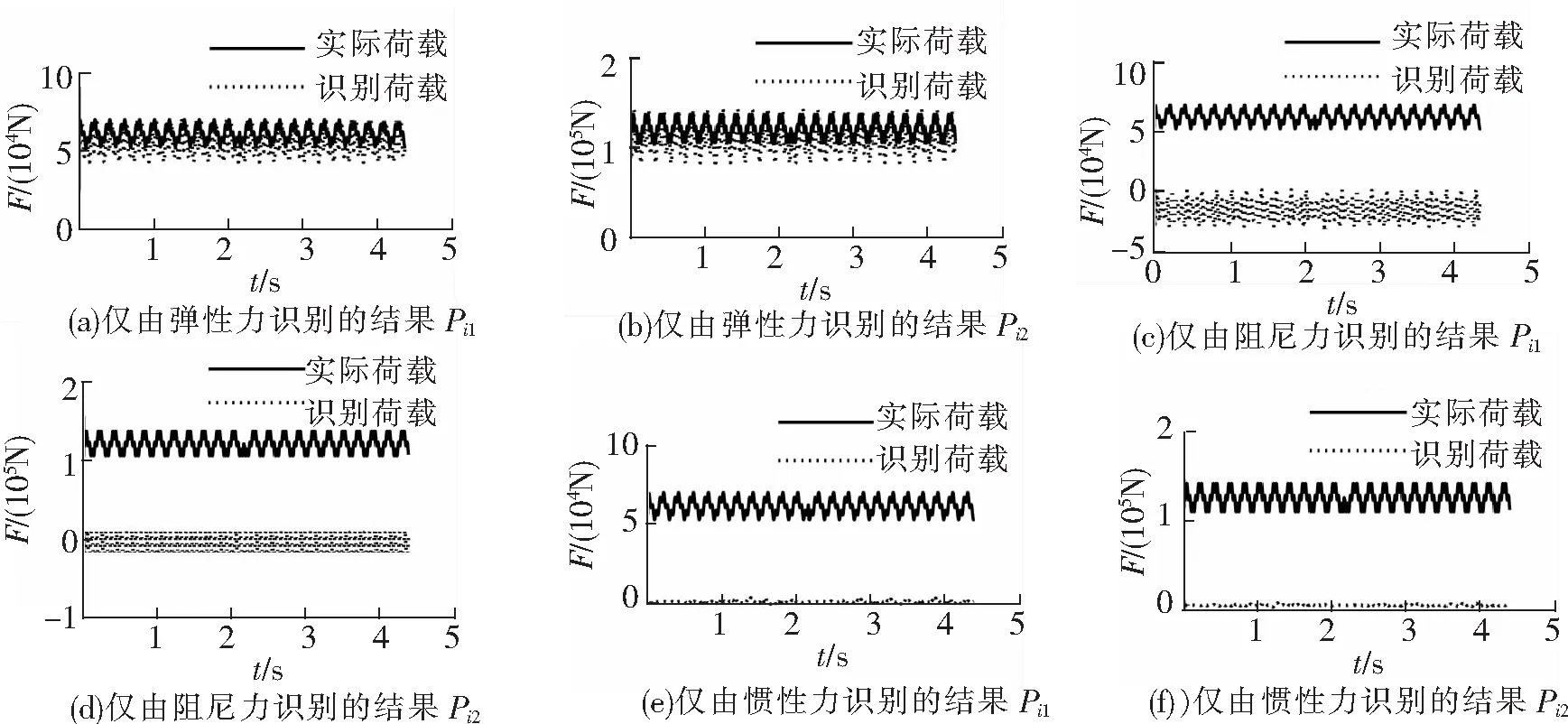
图7 识别荷载与实际荷载对比图

计算弹性力、阻尼力和惯性力在移动荷载识别中所占的比重w，计算结果如表2所示。

(15)

由表2可以看出，弹性力对荷载识别结果的影响最大，约占90%;其次是阻尼力，占10%左右;惯性力对荷载识别的影响最小，只有0.04%左右。实际应用时可以不考虑加速度的影响，以提高荷载识别效率。

表2 弹性力、阻尼力和惯性力在移动荷载识别中所占的比重w %

4.2 荷载移动速度的影响

荷载分别以15、20和25 m/s速度移动时，荷载识别结果与图5、图6相似，由于篇幅有限，此处不再赘述。表3为不同车速对应的两跨连续梁荷载识别误差。

表3 两跨连续梁在不同速度下的识别误差

由表3可以看出，随着移动荷载速度的增大，荷载识别误差也相应地在增大，同时随车速的增大，Pi1和Pi2识别误差增长也越来越快，Pi1最大识别误差仅为1.94%，Pi2最大识别误差仅为5.30%。

4.3 荷载大小的影响

当移动荷载以15 m/s的速度在两跨连续梁上移动时，P1(t)和P2(t)在式(16)的3个力中选取，表4和表5中简写为6 268、12 332和15 000。表4为不同移动荷载作用下的Pi1的识别误差，表5为不同移动荷载的作用下Pi2的识别误差。

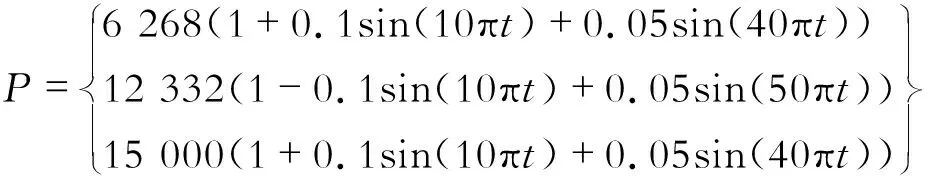
(16)

表5 不同移动荷载的作用下Pi2的识别误差表

由表4可知，Pi1的识别误差几乎不受2个移动荷载大小的改变而改变。由表5可以看出，当P1=P2时，Pi2的识别误差均为1.89%；当P2不变时，Pi2的识别误差随着P1的增大而减小；当P1不变时，Pi2的识别误差随着P2的增大而增大。只有当P1、P2的组合为(12 332、6 268)和(15 000、6 268)时，Pi2的识别误差小于Pi1的识别误差；其他荷载组合时，Pi2的识别误差均大于Pi1的识别误差。因此，Pi1的识别误差稳定，Pi2的识别误差对荷载大小比较敏感，原因可能是由于识别Pi2的动力响应是P2和P1共同作用时动力响应的叠加，造成Pi2的识别误差受荷载大小的影响较大。

4.4 连续梁跨数的影响

仍采用表1所示的参数，只将跨数分别改为3、4时，分析跨数对荷载识别结果的影响情况。表6为不同跨数连续梁的荷载识别误差。

表6 荷载移动速度为15 m/s时，不同跨数连续梁的荷载识别误差 %

由表6可知，随着连续梁跨数的增多误差也在增大，Pi1最大识别误差仅为2.11%，Pi2最大识别误差仅为6.38%。

5 结论

(1)当切比雪夫多项式的项数达到一定值以上时，位移、速度和加速度响应的重构误差均较小，且趋于稳定，采用重构的动力响应可以准确识别出连续梁上的2个移动荷载，Pi1的识别误差小于Pi2的识别误差。

(2)加速度响应对荷载识别结果的贡献很小，工程实际应用时，可只采用位移和速度响应进行连续梁的移动荷载识别。

(3)Pi1的识别误差几乎不受2个移动荷载大小的影响；当P1不变时，Pi2的识别误差随着P2的增大而增大；当P2不变时，Pi2的识别误差随着P1的增大而减小。

(4)移动荷载的识别误差随着荷载移动速度的提高和连续梁跨数的增多而增大。