面向吊索损伤识别方法研究的拱桥实验模型设计

王微微， 苏木标， 杨彦霄， 王 闯

(1.石家庄铁道大学 土木工程学院，河北 石家庄 050043；2.石家庄铁道大学 大型结构健康诊断与控制研究所，河北 石家庄 050043)

王微微，苏木标，杨彦霄，等.面向吊索损伤识别方法研究的拱桥实验模型设计[J].石家庄铁道大学学报(自然科学版),2022,35(1):1-6.

大型桥梁结构的损伤识别，虽然可以通过有限元模拟来研究，但是单纯通过数值模拟进行研究往往有一定的局限性[1-2]。一般也不可能在实际运营的桥上进行损伤模拟实验，除非是准备拆除的废旧桥梁[3]。然而，局部损伤导致的桥梁整体结构力学行为变化也难以通过局部构件实验来模拟。因此，整桥模型实验在桥梁结构损伤识别研究中具有重要意义[4]。根据实验目的的不同，整桥模型实验可分为面向设计研究、面向施工研究、面向结构力学性能研究和面向健康监测与损伤识别研究4种类型。

面向桥梁设计理论研究的整桥模型实验，多为验证设计理论和计算方法的正确性及结构设计的合理性。例如，大连市泉水4号桥设计，由于其矢跨比(1/12)远小于常规拱桥的矢跨比，黄海新等[5]为了验证该桥结构设计的安全性，用有机玻璃制作了该桥的缩尺全桥模型，对其空间力学特性进行了实验研究。李勇等[6]对中承式单拱肋半飘浮体系的伊通河大桥进行了缩尺模型的静动力实验研究，目的是验证有限元数值模拟结果与实际结构力学行为的一致性。面向施工研究的整桥模型实验多为检验施工阶段结构性能的可靠性和施工过程的安全性。例如，李乔等[7]为检验结构在施工及运营阶段能否满足高速铁路桥梁的功能要求, 对九曲河大桥进行了全桥模型实验研究。面向力学性能研究的整桥模型实验，陈宝春等[8]以福建省福鼎市山前大桥为原型，设计制作了一座钢管混凝土(单圆管)单肋拱空间受力实验模型，对拱空间受力全过程进行了整桥模型实验研究。上述整桥实验模型设计的特点是，模型多与某实际桥梁相似，尽量保证模型与实桥二者的受力特点和力学行为的高度一致，要求模型按照相似原理进行设计。而面向损伤识别方法研究的整桥模型实验，由于其测试允许误差的限制和损伤模拟等要求不同，使得该类实验模型设计的特点和要求也将有所不同，此类模型实验鲜见报道。本文以研究基于系梁挠度的吊索损伤识别方法为目的，探求面向损伤识别研究的整桥实验模型设计的原则、思路和方法。

1 模型设计与制作

1.1 设计依据与设计原则

面向损伤识别方法研究的整桥模型实验，其目的是通过模拟结构的不同位置发生不同程度的损伤，测试损伤前后桥梁结构某些响应量的变化，从而验证损伤识别理论和方法的正确性。此类模型实验，不是针对某座具体的实际桥梁，而是针对某种类型的桥梁开展损伤识别方法研究。因此，面向损伤识别方法研究的整桥实验模型不同于以往用于其他目的的模型，它不代表任何一座实际的桥梁，只是着力表现某类桥梁(比如系杆拱桥或斜拉桥等)的主要受力特点。

实验模型主要是为系杆拱桥吊索损伤识别方法研究而设计的，其主要设计依据是拱桥设计规范，再根据室内实验条件、实验目的和测试精度要求，确定实验模型各构件的基本尺寸及荷载等相关参数。该实验模型其实就是依据设计规范为满足实验要求而设计的一座适合室内实验研究的小型系杆拱桥，其设计原则：

(1)满足设计规范要求。

(2)参考相似原理，参照某实际拱桥，确定合适的外形尺寸及相应的细部构造，满足室内实验条件(包括场地及测试精度)要求。

(3)保证实验模型能够准确模拟系杆拱桥不同位置吊索发生不同程度的损伤，并能精确测出有关参数在吊索损伤前后的变化量值。

1.2 确定模型设计基本参数

虽说该实验模型不代表任何一座实际的系杆拱桥，但为了着力表现系杆拱桥的主要受力特点，设计中以某实际公路钢管混凝土下承式系杆拱桥作为参考，尽量按照相似理论进行缩尺，并根据室内实验条件作适当调整，确定模型外形尺寸及相应的细部构造。

参考的原型钢管混凝土下承式系杆拱桥：计算跨径为90 m，桥梁总宽度17.6 m，矢高15 m。

拱轴线为抛物线；拱肋采用双肢钢管，中间用腹杆连接，钢管直径800 mm，管壁厚12 mm，钢管内填C50混凝土；两拱肋肋间设置5道K式横撑，拱脚间采用矩形钢箱梁作为系梁，两侧系梁间采用工字形横梁连接；吊索为55Φ7高强钢丝(极限强度为1 670 MPa)，吊索间距7.5 m。

考虑到模型实验要模拟环境温度变化对吊索损伤识别结果的影响，实验要在温箱里进行，要求模型长度应小于4 m，因此，选定系杆拱桥实验模型跨径为3.6 m，桥面总宽度为0.6 m，矢高0.8 m，拱肋线形为二次抛物线，拱轴线方程为

(1)

即实验模型的基本结构尺寸大致按照1∶25的缩尺比例参考上述原型拱桥确定，如图1所示。

1.3 模型构造与制作

实验模型各构件均采用钢材进行独立加工，然后通过螺栓或焊接等方式进行连接，以方便实验过程中能够模拟不同拱梁刚度比、系杆拱桥不同位置的吊索发生不同程度的损伤。实验模型见图2，其中各构件设计制作的具体细节如下。

1.3.1 吊索的设计与制作

以往研究者多采用松动吊索端锚具、减小吊索横截面面积或减小材料弹性模量的方式来模拟吊索损伤[9]。但这些方法实际操作时，不仅无法精确控制吊索的预设损伤程度，操作极不方便，材料也不能重复利用。最重要的是，吊索损伤后导致吊索下锚固点系梁的挠度变化量比较小，环境和测试条件带来的测量误差会对实验结果有较大的影响。所以，为了方便精确模拟吊索发生不同程度损伤，同时增大吊索损伤前后系梁(在吊索与系梁锚固点处)的挠度变化值，将吊索设计成主要由2部分串联而成，其上端是7股钢丝捻制而成的直径为3 mm的钢芯钢丝绳，下端为由8根刚度相近的弹簧并联而成的吊索损伤模拟装置。吊索上同时还串联了其他附件，包括S形拉力传感器(用于测量索力)和法兰螺栓(用于调整系梁线形和索力)，如图3所示。这样设计的吊索，其整体刚度主要由8根并联弹簧决定，可以用减少弹簧数量的方式精确模拟吊索发生不同程度的损伤，并且吊索损伤后的变形也主要由弹簧的变形决定。此外，设计此吊索时应注意每根弹簧的刚度要合适，既要保证吊索损伤前后系梁的挠度有明显的变化(可精确测量)，还要保证吊索损伤(弹簧数量减少)后其变形满足线弹性要求。

1.3.2 拱肋及系梁的设计与制作

为了验证吊索损伤识别方法对不同拱梁刚度比系杆拱桥的适用性，实验模型设计了2套刚度不同的拱肋和3套刚度不同的系梁。2套拱肋分别是外径为60 mm(壁厚为5 mm)和外径为50 mm(壁厚5 mm)的圆形钢管；3套系梁分别为3 mm、4 mm、5 mm厚(宽度为600 mm)的钢板。不同的拱梁组合可做成拱梁刚度比不同的系杆拱桥。系梁既承担两端拱脚处的水平推力，又作为桥面板承担桥面的竖向荷载。当需增大系梁(钢板)的抗弯刚度时，可在其原两侧再用螺栓分别加上1根40 mm×40 mm×4 mm等边角钢。

1.3.3 横梁的设计与制作

横梁采用40 mm×40 mm×4 mm等边角钢，全桥共设11根横梁，分别在11对吊索与系梁连接处通过螺栓与系梁连成一体，横梁两端与吊索之间用法兰螺栓连接，承托系梁并将系梁承担的荷载通过吊索传递给拱肋。系梁上的配重均匀分散悬挂在各横梁两端。

1.3.4 拱肋与系梁之间连接装置的设计与加工

为了保证拱肋与系梁之间连接成为刚接，专门设计加工一套(4个)刚度较大的连接装置。该装置采用钢板焊接而成，分别与拱肋和系梁通过螺栓连接。拱肋与系梁通过连接装置用螺栓连成一体，便于不同刚度的拱肋和不同刚度的系梁组合成拱梁刚度比不同的系杆拱桥。

1.3.5 拱肋之间的横撑设计

横撑主要起横向稳定作用，保证两侧拱肋形成空间结构体系，以便共同承担横向荷载。为加工方便，全桥在跨中附近共设置4道间距为0.3 m的横撑。2套拱肋的横撑均采用外径为50 mm(壁厚为5 mm)的钢管，拱肋与横撑之间以焊接方式连接。

1.4 模型配重设计

因为模型各结构构件均拟采用钢材加工制作，单纯按照前文提出的设计准则设计的模型质量太小，又因为模型实验是以研究基于系梁挠度的吊索损伤识别方法为目的，当属静力实验范畴。如果模型的质量太小，恒载引起的结构内力和变形太小，无法准确量测实验模型因吊索损伤而引起的内力和变形的变化量值。因此，需要对模型系梁进行适当的配重。通过有限元计算，为使得模型系梁在吊索发生最小损伤(模型可模拟的最小损伤是吊索刚度降低12.5%)时，损伤吊索与系梁锚固点处挠度差在0.2 mm以上，且综合考虑实验条件的限制，最终决定按照系梁质量的6.75倍对系梁进行配重,并根据实验目的要求，将配重集中加载在系梁上。

2 实验模型适用性检验

为检验实验模型对吊索损伤识别方法研究的适用性，先对实验模型进行有限元分析，通过改变吊索刚度模拟不同位置吊索发生不同程度损伤，分析吊索损伤前后系梁挠度变化规律，再用实验模型实际模拟不同位置吊索发生不同程度损伤，测量吊索损伤前后系梁挠度变化量值。

有限元分析时，拱肋、横梁、系梁、加劲角钢、横撑均采用梁单元，吊索采用只受拉不受压的桁架单元和弹簧单元串联的方式进行模拟，系梁(即桥面板)采用四节点壳单元，拱脚与系梁之间为固结，整桥与基础之间的约束两端均为铰支。根据实验模型摆放位置(东西向)，为说明问题方便，北侧吊索编号从东到西分别为：N1、N2、N3、N4、N5、N6、N7、N8、N9、N10、N11；南侧吊索编号从东到西分别为：S1、S2、S3、S4、S5、S6、S7、S8、S9、S10、S11。实验模型可模拟多种拱梁刚度比，篇幅所限，仅列出其中一种的验证结果。实验之前，先进行调索(包括索力和线形)，调整后的吊索索力如表1所示。由表1可知，调整后的初始索力分布均匀，且与有限元结果吻合良好，可以此为系杆拱吊索未发生损伤的初始状态。同时在各吊索与系梁连接点处安装激光位移传感器测量系梁各点挠度的变化值，传感器布设见图2。

为验证实验模型在吊索损伤前后系梁挠度差(即系梁与各吊索连接点处的挠度改变量)对吊索损伤反应的灵敏性，设置了24种吊索损伤工况。前12种为单根吊索损伤工况，依次设置损伤吊索为N3、N4、N6,并分别考虑损伤程度β为12.5%、25%、37.5%、50%；工况13～24为2根吊索同时损伤，依次设置损伤吊索为N5&N6、N5&N7、N4&N8和N6&S6，详见表2。

表2 损伤工况

实验时对应去掉1～6根弹簧，模拟吊索刚度损伤程度β分别为12.5%、25%、37.5%、50%、75%，并用激光位移计测量各吊索与系梁连接点处系梁的挠度差，与各损伤工况下数值模拟的结果进行对比分析。因篇幅所限，仅给出工况9、12、13、14的结果图，其中前2种为单索损伤，见图4；后2种为双索同时损伤，其结果见图5。其他工况仅将损伤吊索与系梁锚固点处的挠度差提出，列于表3与表4之中。

图4 N6(吊索)发生不同程度损伤对应的系梁挠度差分布曲线

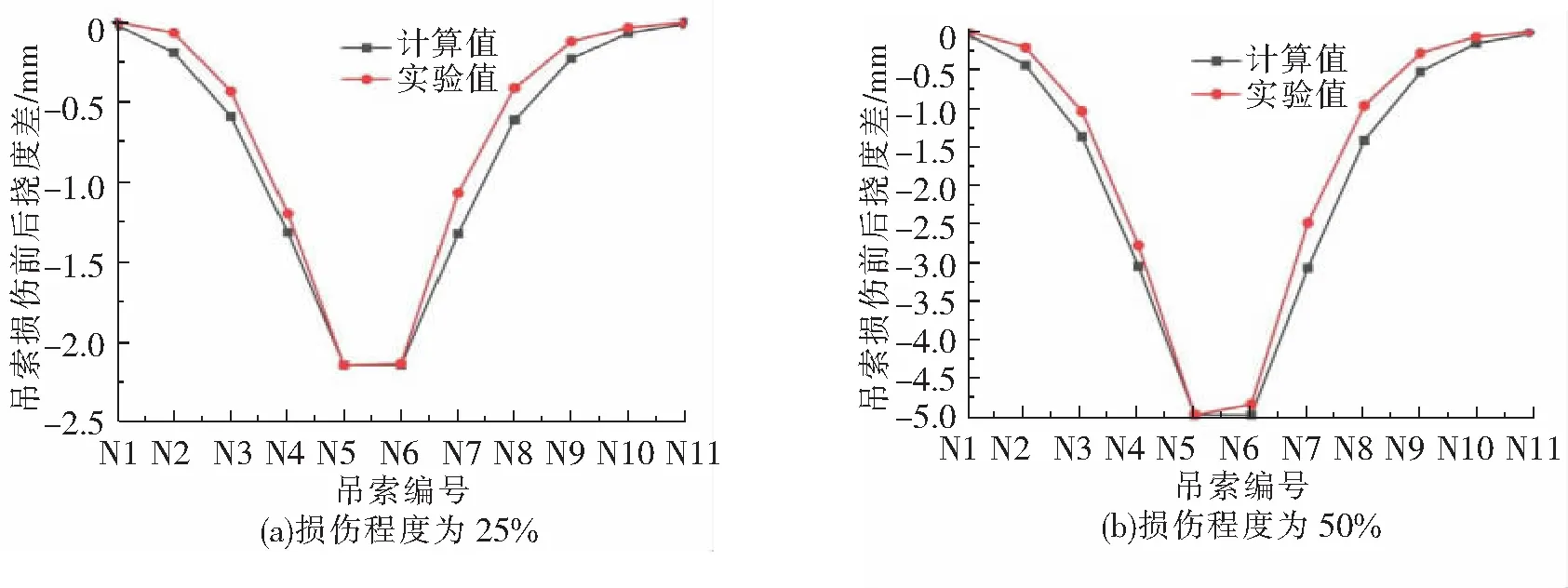
图5 N5& N6(双索同时损伤)不同程度损伤对应的系梁挠度差分布曲线

表3 单索不同损伤程度对应的系梁挠度差

表4 2根索同时损伤(不同损伤程度)对应的系梁挠度差

由图4和图5可以看出，无论单索还是双索损伤，实验结果均与数值结果吻合良好。且从表3及表4可以看到，实验结果与数值结果在单索损伤时最大误差为5%，2根索同时发生损伤时最大误差为4.8%，即使当吊索发生的损伤比较小(如12.5%)时，系梁的挠度差也可较准确测得。由此可见,该实验模型完全可以满足基于系梁挠度的吊索损伤识别方法研究的各项实验要求。

3 结语

根据基于系梁挠度的拱桥吊索损伤识别方法研究模型实验的目的，分析了面向吊索损伤识别方法研究的实验模型的特点和要求，设计了一套系杆拱桥实验模型。该拱桥模型既不同于以往用于其他目的的实验模型，也不代表任何一座实际的拱桥，只是着力表现系杆拱桥(此类桥梁)的主要受力特征，并便于实验过程中各种实验数据的精确测量。

该实验模型设计的主要依据是拱桥设计规范，并根据室内实验条件、实验目的和测试精度要求确定实验模型各构件的基本尺寸及荷载参数。设计的关键是要保证模型能够准确模拟系杆拱桥不同位置吊索发生不同程度的损伤，并能精确测量出系梁挠度和索力在吊索损伤前后的变化量。实验对比分析结果表明，该实验模型完全可以满足基于系梁挠度的吊索损伤识别方法研究的各项要求，其设计思路和方法对其他桥梁损伤模拟实验研究具有参考意义。