登陆台风近地面环境压力分布实测与建模

艾祖斌， 李文强， 侯圣均， 贾帅动, 张芳馨

(1.中电建路桥集团有限公司，北京 100048；2. 同济大学 土木工程防灾国家重点实验室，上海 200092)

艾祖斌，李文强，侯圣均，等.登陆台风近地面环境压力分布实测与建模[J].石家庄铁道大学学报(自然科学版),2022,35(1):113-119.

0 引言

近年来，中国沿海地区台风频发，而不断兴建的大跨、高耸结构对于使用寿命期内的极大风速作用十分敏感，有必要合理预测目标重现期内台风极值风速，为建筑结构的安全设计与风险评估提供合理依据。运用成熟的台风数值模型预测台风极值风速是国际上普遍认可的做法。

在台风极值风速的预测以及台风灾害的评估中，台风径向风速剖面的精确计算至关重要。大多数学者都是基于实测数据进行统计拟合，给出台风径向风速剖面的经验公式，如Schloemer[1]，Atkinson et al[2]。1980年， Holland[3]做了创新的改变，首次将Atkinson et al[2]和Dvorak[4]得出的台风风压分布经验函数与台风气旋径向压力梯度平衡方程结合，得出台风径向风速分布函数解析模型。该解析模型的优点是仅含单一参数，即台风径向风压分布系数β，但仍需用实测数据进行系数β值的估算。应用Holland解析模型对大西洋和澳大利亚地区的台风进行数值模拟计算，发现拟合结果比其他经验函数模型具有更高的精度。

基于敏感度分析方法的研究结果表明[5-6]，台风风压分布系数β对于确定工程场地重现期设计风速具有较大影响。为此，利用浙江省内数百个近地站点实测气压数据，提出了一种基于近地面多点压力分布实测的台风风压场研究方法，以对风压分布系数β进行相关研究。

1 台风气压场分布模型

台风的径向风压分布，国外较早就做了大量的实测，得到了较多的实测数据资料。为了消除不同台风中心和不同大气压对实测结果变异性影响，对台风风压实测数据进行标准化处理

Φ=(Pr-Pc)/(Pa-Pc)

(1)

式中,Pr为距离台风中心r处的风压;Pc为台风中心气压;Pa为自然大气压，理论上是r无穷大处的气压。

在实测数据基础上，许多学者如Depperman[7]、Schloemer[1]的研究结果表明台风的径向风压分布服从幂指数关系，Holland统一用函数式表示

(2)

式中，ΔP为台风中心低压差，ΔP=Pa-Pc;Rmax为最大风速半径；β为风压分布系数，即Holland参数，当β=1时，就是Schloemer等式。

台风气旋径向压力梯度平衡方程

(3)

式中,ρA为空气密度;Pr为风场压力分布函数;r为距离台风中心的半径;v为空气微团距离台风中心r处的切向平均风速;f为Coriolis参数，f=2ΩsinΨ，Ω为地球转动速度，Ψ为空气微团所处的纬度。由式(3)得到

(4)

(5)

(6)

式中,e为自然对数的底数，e=2.718 28;[100]表示将hPa转换成Pa。

2 径向压力分布系数

风压分布系数β的取值影响台风的数值模拟精度，估计风压分布系数β主要有2种方法：一种方法是对地面气压数据进行回归分析得到参数的估计值；另一种方法是通过气压梯度平衡方程得到梯度风速，再通过与上部摩擦层的风速数据进行比较。Vickery et al[8]对这2种方法进行了比较。采用第一种方法，在台风发展的不同阶段，风场的不同地点，参数β都是变化的，因此很难获得Holland参数β的确定值，但是这种方法却在一定程度上反映了Holland参数β的变化规律。采用另一种方法，Holland参数β可以表示为中心气压差和最大风速半径的函数。Love et al[9]、Hubbert et al[10]、Holland et al[11]、Jakobsen et al[12]、Fema[13]、Holland[14]都曾提出计算台风风压分布系数β的方法。

2008年，Holland提出风压分布系数β新的计算公式，认为影响参数β的因素很多，包括台风中心气压及其随时间的变化、台风移动速度、台风风速剖面、台风中心经纬度，计算表达式如下

(7)

(8)

x=0.6(1-ΔP/215)

(9)

式中,ΔP为中心压差；∂pc/∂t为中心气压强度的变化；ψ为台风中心纬度绝对值；vT为气旋移动速度;vmg/vm为梯度风到海面风的转换因子。

3 近地面多点压力分布实测的台风风压场研究方法

国外学者很早就利用探空雷达、飞机飞行等气压实测数据，获得了台风径向风压分布系数β的计算方法，而国内基于气压实测数据获得台风径向风压分布系数β计算方法的相关研究尚未有可借鉴的工作，这一领域的空白有待填补。为对风压分布系数β进行相关研究，提出了一种近地面多点压力分布实测的台风风压场研究方法。

3.1 浙江省内观测站点气压数据介绍

在浙江省气象局的帮助下，收集到中国沿海及内地上千个近地观测站点对台风卡努(Khanun 0515)、韦帕(Wipha 0713)、罗莎(Krosa 0716)、莫拉克(Morakot 0908)等4个台风登陆及移动过程中实测到的气压数据，浙江省有观测记录的观测站点地理位置分布如图1所示。台风观测记录数据包含观测时间、观测站点名称、经纬度、海拔高度、温度、气压等数据信息，以台风韦帕(Wipha 0713)为例，其路径及中国沿海与内地大量近地观测站点地理位置分布如图2所示。

图1 浙江省有观测记录的观测站点地理位置分布图

图2 台风韦帕(0713)路径和近地观测站点位置选取、处理示意图

3.2 基于近地面环境压力分布实测的台风风场研究方法

由大气压相关研究资料和相关规范可知，地表某一点的大气压值主要由该点的海拔高度、大气温度决定，受该点所处的地表类型、地貌特征影响甚微，且已知该点的海拔高度、大气温度，可以将该点的大气压值换算到该点海平面气压值。假定某一台风影响范围内有足够多的近地观测站点实测气压数据，利用上述特性，可以对该台风的海平面风压场进行重构并对气压场分布特征进行研究。基于收集到的4个台风的近地观测站点实测气压数据，提出了基于近地面环境压力分布实测的台风风压场研究方法，详述如下。

波特兰国家航天协会(Portland State Aerospace Society，PSAS)于2004年给出大气压随海拔高度和大气温度变化的修正公式

(10)

T0=T+Lh

(11)

式中,PSLP为海平面气压；P为观测站点气压；h为观测站点海拔高度；L为大气温度随海拔上升的下降率，L=0.006 5 K/m；g为重力加速度；M为大气摩尔质量，M=0.028 964 4 kg/mol；R为大气摩尔常量，R=8.314 47 J/(mol·K)；T0为海平面大气温度；T为观测站点温度。利用大气压随海拔高度和大气温度变化的修正公式，将收集到的近地观测站点在不同位置、不同海拔和不同温度条件下实测到的气压数据统一修正为海平面气压。

计算台风风压分布系数β时，需引入台风最大风速半径Rmax，而实测资料和热带气旋年鉴资料[15]并未提供台风最大风速半径Rmax的实测值，因此可参考Yasui et al[16]由台风实测记录拟合得到的台风中心压差与最大风速半径之间的经验函数关系式，确定Rmax的取值，并给出经验公式的适用条件：

(1)台风中心气压低于980 hPa。

(2)台风中心距离工程场地100～500 km。

(3)工程场地地表气压低于1 000 hPa。

E(Rmax)=2.06×104ΔP-1.27

(12)

σ(Rmax)=4.4×104ΔP-1.76

(13)

式中,E(Rmax)、σ(Rmax)分别为Rmax的均值和方差。

台风的径向风压和风速分布是指过台风中心某一剖面上的风压和风速与离台风中心距离的函数关系。实际中，由于近地观测站点不可能分布或集中在台风空间结构中的一个径向剖截面上，考虑到台风空间结构，在近地观测站点风压数据处理过程中，认为距离比较近的2个平面间区域内的近地观测站点风压数据是台风一个径向剖截面上的点风压数据。在近地观测站点风压数据处理和计算过程中，台风影响范围半径取为350 km，2个平面间的距离取为30 km。

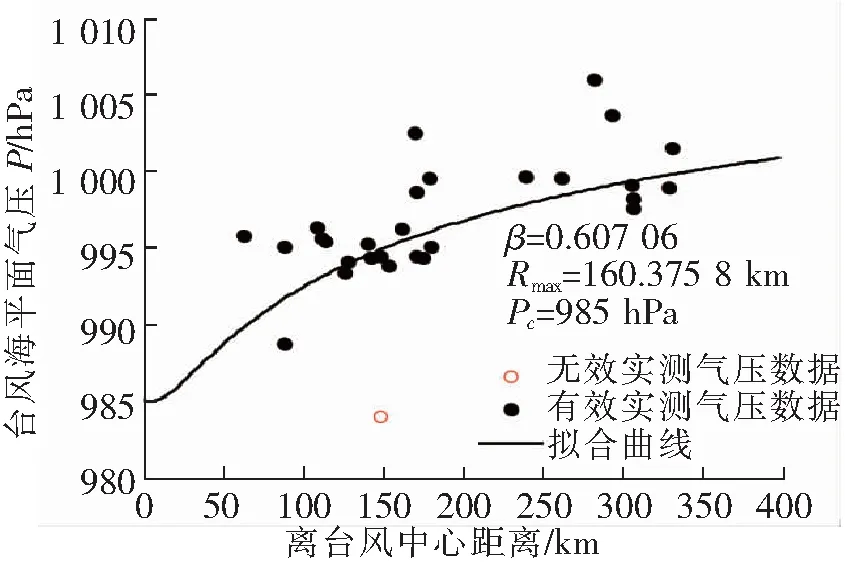
图3 台风韦帕(0713)近地观测站点海平面气压数据处理结果

利用上述选取近地观测站点的方法，获得该时刻含近地观测站点最多方向上的台风径向剖截面上的海平面气压数据，结合《热带气旋年鉴》提供的台风中心气压数据资料，利用Holland台风气压场分布模型和本文提出的台风最大风速半径Rmax计算方法，获得台风韦帕2007年9月19日09时的径向风压分布曲线和风压分布系数β的值，结果如图3所示。

既有研究结论表明，台风是个非对称结构，不同方向的径向风压与风速分布不同，有必要对台风不同方向的径向风压分布进行研究。图4是基于台风韦帕(Wipha 0713)2007年9月19日11时的近地观测站点实测气压数据，利用近地面多点压力分布实测的台风风压场研究方法，结合Holland台风气压场分布模型和本文提出的台风最大风速半径Rmax计算方法，拟合得到不同方向上的风压分布系数β的值。从图4来看，不同方向上的风压分布系数β的值不同，即不同方向上的径向风压分布不同；16个标准方向中，西南方向(SW方向)的风压分布系数β的值最小，为0.059 7；东北偏北方向(NNE方向)的风压分布系数β的值最大，为0.218 2；16个方向的风压分布系数β的平均值为0.132 0。

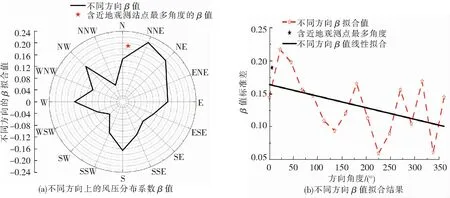
图4 台风韦帕(Wipha,0713,2007年9月19日11时)不同方向的β值示意图

图5 台风韦帕(0713)中心气压及风压分布系数β值及标准差变化示意图

图5展示了台风韦帕2007年9月16日08时到2007年9月20日13时的中心气压和2007年9月18日13时到2007年9月20日10时的台风风压分布系数β值及标准差变化。

从图5来看，在台风韦帕(0713)登陆过程中，台风风压分布系数β的值随台风韦帕强度的减弱而迅速减小；风压分布系数β值标准差在台风强度减弱的过程中有轻微波动但基本保持稳定。

3.3 参数对台风风压分布系数β的影响

根据国外学者研究资料，台风风压分布系数β的值与台风最大风速半径、台风中心压差、台风中心所处纬度及海平面温度有关。获得台风中心压差ΔP、最大风速半径Rmax和台风中心位置北纬纬度Ψ对风压分布系数β的影响，结果如图6～图8所示。

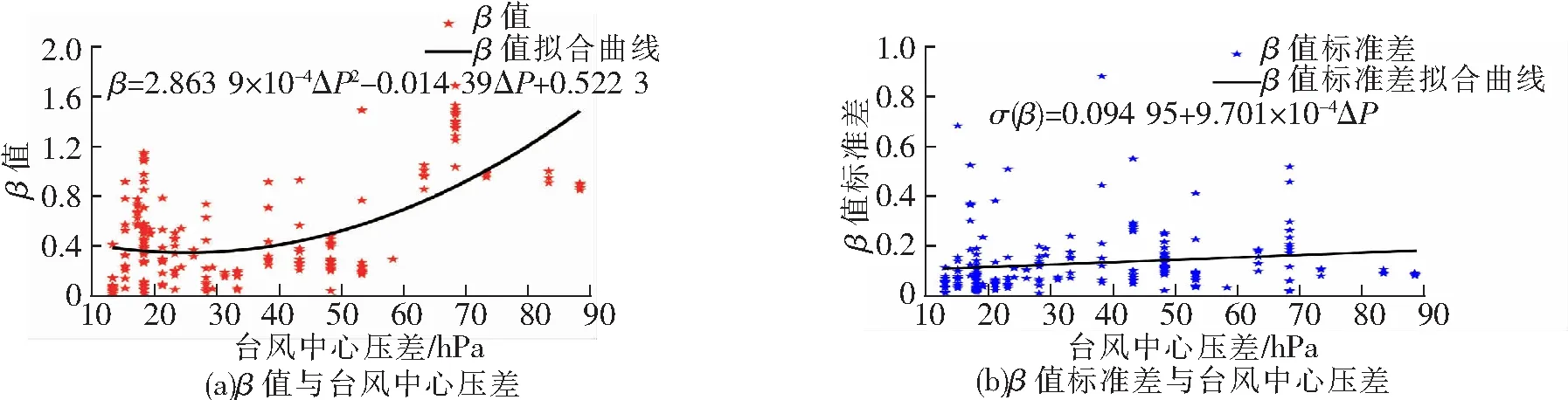
图6 台风中心压差对风压分布系数β值及其标准差的影响

图7 台风最大风速半径对风压分布系数β值的影响

图8 台风中心北纬度对风压分布系数β值及其标准差的影响

从图6～图8来看，台风中心压差ΔP和最大风速半径Rmax对风压分布系数β的值及其标准差影响较大，台风中心北纬度Ψ对风压分布系数β的值及其标准差影响较小。综上，只考虑台风中心压差ΔP和最大风速半径Rmax对风压分布系数β值的影响，采用最小二乘法拟合得到风压分布系数β值及其标准差与台风中心压差ΔP和最大风速半径Rmax的函数关系式

β=4.102 5×10-5(ΔP)2+0.029 3×ΔP+0.0795 9×ln(Rmax)-4.601 0

(14)

σ(β)=-0.002 7×ΔP-0.131 1×ln(Rmax)+0.881 5

(15)

利用由最小二乘法获得的风压分布系数β及其标准差计算公式(式(14)和式(15))分别对卡努、韦帕、罗莎、莫拉克4个台风移动过程中的风压分布系数β的值进行计算，计算结果如图9所示。

图9 台风中心气压及风压分布系数β值拟合曲线示意图

从图9来看，台风风压分布系数计算方法获得的系数β的值与由实测数据拟合得到的某个时刻β的值有一定偏差，从卡努、韦帕、罗莎、莫拉克4个台风整体效果来看，引入标准差后β的值取值范围基本涵盖由实测数据拟合得到的不同时刻β的值。

4 结论

通过剖析Holland台风径向风速和风压分布函数模型和基于Holland台风风速和风压分布函数、Yasui确定Rmax的经验函数和实测数据，对比目前各学者提出的台风风压，提出了一种基于近地面环境压力分布实测的台风风压场研究方法，得到以下结论：

(1)Holland模型引入的台风风压分布系数β的取值对计算结果影响较大，有必要根据实测数据统计和分析出工程场地处台风径向风压分布系数β的取值。

(2)台风中心压差ΔP和最大风速半径Rmax对风压分布系数β的值及其标准差影响较大，台风中心北纬度Ψ对风压分布系数β的值及其标准差影响较小。

(3)台风风压分布系数计算方法获得的系数β的值与由实测数据拟合得到的某个时刻β的值有一定偏差，引入标准差后的β的值取值范围基本涵盖由实测数据拟合得到的不同时刻β的值。