探析2021年高考中的数列最值问题
李富春
(云南省玉溪第一中学,653100)
我们知道数列是定义域为正整数集的函数,因此,在处理数列最值问题时,函数方法仍然是最基本也是最重要的方法[1].但是,在2021年高考中,涌现出的数列最值问题,仅用函数方法是不能解决的,这就给考生提出了新的挑战.为此,笔者以2021年高考中的数列最值(取值范围)问题为例,就怎样求解进行一些归纳、总结、探析,以飨读者.
一、 先计算后检验
先计算后检验也叫先猜后证,在这里是指先猜想出符合题意的一个数列,通过计算,然后代回检验,便可得出答案.
例1(2021年北京高考题)设数列{an}是递增的整数数列,若a1≥3,a1+a2+…+an=100,则n的最大值为( )
(A) 9 (B) 10 (C) 11 (D) 12


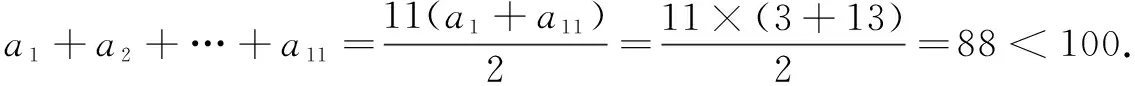
故选C.
评注先猜后证是探究数学问题的一种常用策略.
二、先放缩后求和
若要求一个数列{an}的前n项和Sn的最值(取值范围),但又不能用常规方法求出Sn,要转化为求函数的最值(取值范围)问题,可通过先放缩后求和的方法联系裂项法或等差、等比数列解决问题.

(B) 3 评注放缩后求和,要考虑放缩的程度且便于用常规方法求和. 先分类讨论,求出数列的项的取值范围或值,然后求出数列的前n项和,再比较前n项和的大小,使问题获解. 例3(2021年上海高考题)已知ai∈N*(i=1,2,…,9),对任意的k∈N*(2≤k≤8),ak+1=ak+1和ak-1=ak-1有且仅有一个成立,a1=6,a9=9,则a1+a2+…+a9的最小值为______. 解因为ak+1-ak=1和ak-ak-1=1有且仅有一个成立,令bk=ak+1-ak,则bk=1和bk-1=1有且仅有一个成立,即bk和bk-1中仅有一个为1. 又2≤k≤8(k∈N*),所以b2和b1中仅有一个为1;b3和b2中仅有一个为1;b4和b3中仅有一个为1;b5和b4中仅有一个为1;b6和b5中仅有一个为1;b7和b6中仅有一个为1;b8和b7中仅有一个为1. 若b1=b3=b5=b7=1,则由a1=6,可得a2=a1+1=7.进而a3≥1(因为a3是正整数),得a4=a3+b3=a3+1≥2;进而a5≥1(因为a5是正整数),得a6=a5+b5=a5+1≥2,进而a7≥1(因为a7是正整数),得a8=a7+b7=a7+1≥2.又a9=9,所以a1+a2+…+a9≥6+7+1+2+1+2+1+2+9=31. 若b2=b4=b6=b8=1,则由a9=9,可得a8=a9-1=8.由a1=6,可知a2≥1(因为a2是正整数),a3=a2+b2=a2+1≥2;故a4≥1(因为a4是正整数),得a5=a4+b4=a4+1≥2;故a6≥1(因为a6是正整数),得a7=a6+b6=a6+1≥2.所以此时a1+a2+…+a9≥6+1+2+1+2+1+2+8+9=32. 综上,a1+a2+…+a9的最小值为31. 评注解答此题的关键是读懂题意.题设条件ak+1=ak+1和ak-1=ak-1有且仅有一个成立是什么意思?如何运用这个条件?由此可推出什么结论? 同学们,若能理解掌握上述解答思路和文[1]给出的5种数列最值的探究策略,可以说无论数列最值问题怎么变化、怎么翻新、怎么创新、怎么新颖、怎么新特,解决数列最值问题都没有困难了.
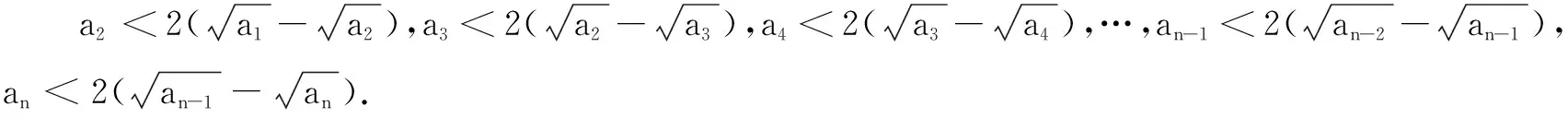

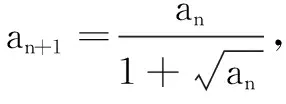


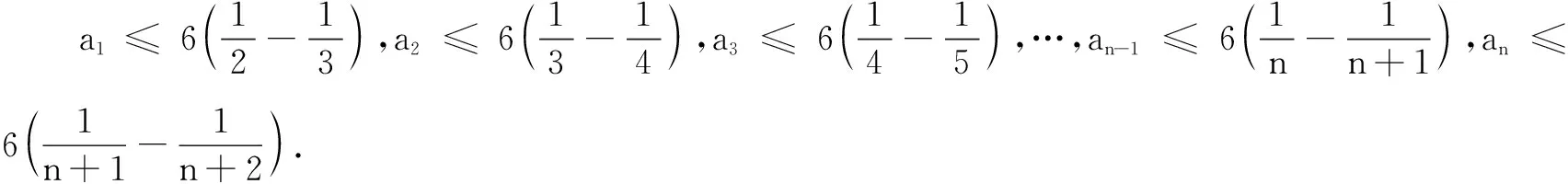

三、先分类讨论,再求和比较

