利用三射线定理巧求空间角
姚素娟 蔡建华
(江苏省常州市第三中学,213000)
一直以来,学生求解空间角的大小一般有两种方案:一是利用综合法求解,二是利用空间向量求解.前者偏纯几何,利用线面、面面、线线间的判定定理、性质定理,利用线面角,二面角的平面角等概念的定义,通过“一作、二证、三求”得出相关空间角的大小,对空间想象能力要求较高;而后者偏纯代数,建立空间直角坐标系,利用空间向量研究线面、线线、面面间的大小与关系,对计算能力要求较高.本文介绍求解空间角大小的第三种途径,即利用三射线定理(也称为三面角的余弦定理),这是一种介于几何与代数之间的一种解题方式,相较前两种方式,过程较为简单便捷.
一、三射线定理及其证明
三射线定理如图1,PA,PB,PC是从点P出发的三条射线,∠APC,∠BPC,∠APB分别为α,β,θ,则二面角A-PC-B的大小φ满足
cosθ=cosαcosβ+sinαsinβcosφ,

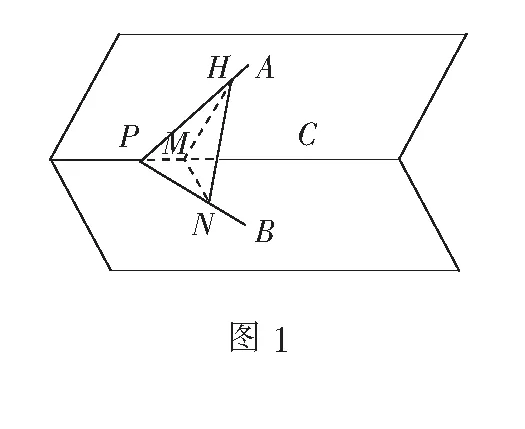
证明如图1,过PC上一点M作二面角A-PC-B的平面角∠HMN,点H,N分别在射线PA,PB上.
证法1利用空间向量

证法2利用余弦定理

cosθ=cosαcosβ+sinαsinβcosφ.

二、应用举例
例1(1982年美国数学会试题)一个正四面体和一个正四棱锥的所有棱长都相等,将正四面体的一个面和正四棱锥的一个侧面紧贴重合在一起,得到一个新的几何体.试问该新的几何体有几个面?
分析如图2,探索新的几何体有几个面,实际上就是探索新的组合体中面FCA与面DAC是否在同一个平面,也就是证明二面角F-AC-B与二面角B-AC-D的平面角之和是否为π.若其和为π,则点F,A,D,C共面.
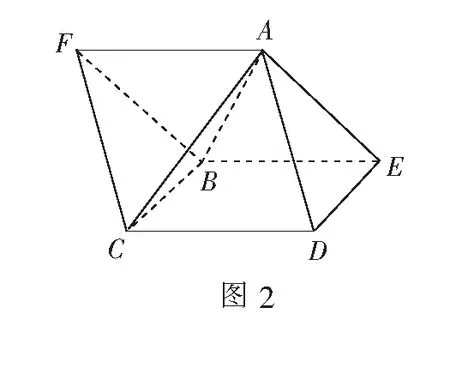
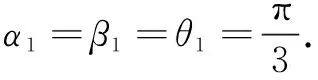

因为cosφ1+cosφ2=0,所以φ1+φ2=π,即F,A,D,C四点共面.同理F,A,E,B四点共面,故新的几何体共有5个面.
评注利用三射线定理求解本题,既不用为如何作出二面角的平面角煞费苦心,也不用为求平面的法向量而穷苦计算,需要的仅仅是找准相关的角,代入公式进行计算并不繁琐.
例2(2020年全国高考题)如图3,在长方体ABCD-A1B1C1D1中,点E,F分别在棱DD1,BB1上,且2DE=ED1,BF=2FB1.
(1)证明:点C1在平面AEF内;
(2)若AB=2,AD=1,AA1=3,求二面角A-EF-A1的正弦值.

分析第(2)问若利用三射线定理,需求出斜角∠AEA1的余弦值,陪角∠AEF,∠A1EF的正余弦值,便可求出正角A-EF-A1的大小.
解(1)略.
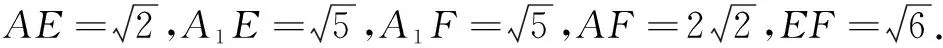


评注本题中的空间图形是长方体,建立空间直角坐标系并利用空间向量解决也不复杂,需要的就是耐心计算两个平面的法向量.考试时可利用空间向量书写,在草稿纸上用三射线定理来验证,这样既避免丢分也能做个检验.
例3(2017年全国高考题)已知a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转.现有下列结论:①当直线AB与a成60°角时,AB与b成30°角;② 当直线AB与a成60°角时,AB与b成60°角;③ 直线AB与a所成角的最小值为45°;④ 直线AB与a所成角的最大值为60°.其中正确的是______.(填写所有正确结论的编号)
分析平移a,b与AC交于点C(平移直线记为a′,b′),由题意可构建以a′,b′,AC分别为x,y,z轴的空间直角坐标系,设a′,b′与AB所成角为α,β,两次利用三射线定理,找到α,β之间关系,从而对相关选项作出判断.
解如图4,过点C作直线a′∥a,b′∥b,作BN⊥a′,BM⊥b′,点N,M为垂足.分别连结AN,AM,设∠ABM=α,∠ABN=β,则由异面直线所成角的定义,可知AB与a所成角即为α,AB与b所成角即为β.
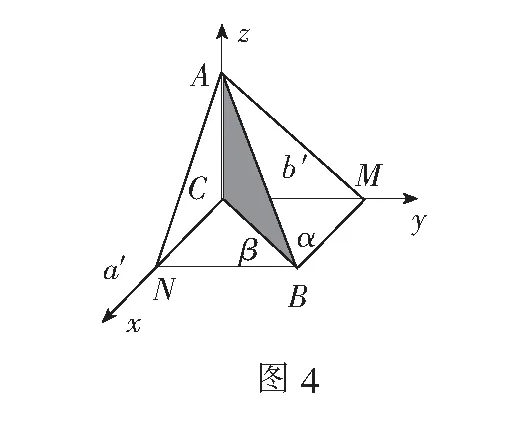




评注本题中三射线定理实则是退化的三余弦定理,采用该解法能方便地找到α,β之间的内在关系.如果该题采用常规几何方法,因为线段AB在旋转,一些数量,角度不便求出,相对来说更考验空间想象能力,有较大难度.
三射线定理虽好,使用时却有两点提醒:一是定理涉及的角较多,且兼有正弦与余弦函数,记忆起来有一定的难度,使用时一定要将公式记牢,不同的角加以命名区分;二是该定理属于课外补充知识,在高考解答题中切不可直接使用,可利用该定理解决选择与填空等客观题,或用来验证解答题答案的正确与否.求解解答题的过程中在避免不了使用时可先证明再使用.学生了解此法在解题时便会多一种路径,有利于求异思维与创新思维的培养.

