妙用反函数性质求解相关综合问题
熊 伟
(安徽省芜湖市汤沟中学,241000)
指数函数y=ax(a>0,a≠1)与对数函数y=logax(a>0,a≠1)互为反函数,二者的定义域和值域互换,且图象关于直线y=x对称.灵活利用反函数关系解题,既可以加深对概念、性质的理解和掌握,又能提高运用函数思想方法分析和解决问题的能力.下面举例说明反函数法在求解有关指数、对数函数的综合问题中的应用.
一、求表达式的值
例1已知曲线y=lnx在A(x1,y1),B(x2,y2)两点处的切线分别与曲线y=ex相切于C(x3,y3),D(x4,y4),则x1x2+y3y4的值为( )


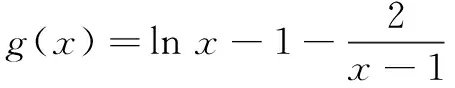

解法2因为函数y=lnx与y=ex互为反函数,所以曲线y=lnx与y=ex关于直线y=x对称.不妨取点A(x1,y1)与D(x4,y4)关于直线y=x对称,则y4=x1,同理y3=x2.

所以x1x2+y3y4=x1x2+x2x1=2,选B.
评注本题是单选题,对比以上两种解法,可见应用y=lnx与y=ex互为反函数的图象对称关系,借助于特殊点能大大简化解题过程,巧求定值.
二、判断大小关系
例2已知直线y=-x+2分别交函数y=ex和y=lnx的图象于点A(x1,y1),B(x2,y2),则下列结论正确的是( )
(A)x1+x2=2
(C)ex1+ex2>2e
(D)x1lnx2+x2lnx1<0
解由y=ex与y=lnx互为反函数,得y=ex与y=lnx的图象关于y=x对称.

由y=-x+2分别与y=ex与y=lnx的图象交于点A(x1,y1),B(x2,y2),作函数的图象如图1,则线段AB的中点坐标为(1,1).
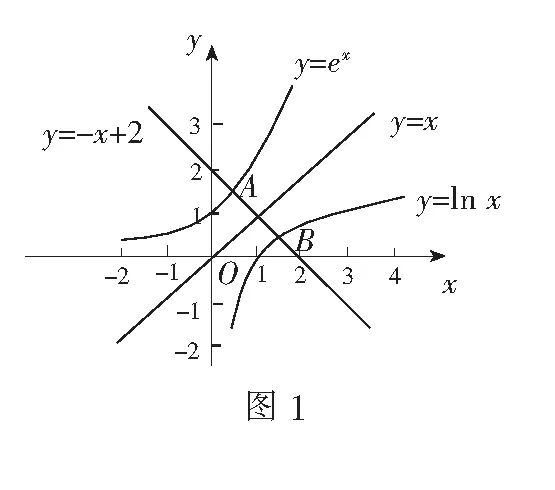
对选项B,将y=-x+2与y=ex联立,可得-x+2=ex,即ex+x-2=0.

综上,选ACD.
评注本题首先应用y=ex与y=lnx互为反函数的图象关系得出AB的中点坐标,再利用函数与方程思想、零点存在定理,结合基本不等式和对数的运算性质等知识作出判断,体现了反函数法与其他知识的综合应用.
三、求参数的取值范围







解法2由函数y=lnx+lna+2的图象在直线y=x的下方,得lnx+lna+2≤x恒成立,即lna+2≤x-lnx恒成立.
设h(x)=x-lnx,则lna+2≤h(x)min.




