基于S 变换行波能谱矩阵相似度的柔性直流单端保护方案

权文杰，童晓阳，张广骁

（西南交通大学电气工程学院，四川省 成都市 610031）

0 引言

柔性直流电网能解决传统直流输电换相失败、谐波含量较高等问题，成为未来构建全球能源互联的关键［1-2］。但柔性直流电网在直流侧发生故障时，其故障电流具有上升速度快、幅值大的特点，在数毫秒之内危及整个电网，主保护需要在2～5 ms 内实现准确的故障识别［3］，保证系统安全运行［4］。

国内外学者已针对柔性直流线路保护提出许多保护方案。根据是否需要信道通信，分为双端量保护和单端量保护。文献［5］根据区内、区外故障时线路两端电流突变方向的不同，构建以电流突变量夹角余弦值为判据的纵联保护，原理简单，计算量小。文献［6］根据故障过程中注入线路的电荷量极性，构建保护判据，不受线路参数影响，但采集时间窗太长，速动性难以保证。文献［7］应用行波差动电流构建保护判据，克服差动电流在区外故障后短时波动引起的延时问题，提高动作速度。文献［8］通过动态时间弯曲距离（dynamic time warping，DTW）算法衡量两侧波形相似度，作为保护判据。考虑到远距离通信时延，双端量保护无法满足柔性直流电网保护速动性要求，所以单端量保护仍是柔性直流保护的首选。

单端量保护算法大多利用限流电感电压变化及其对高频分量的衰减原理构建保护方案［9］。文献［10］提出基于故障极限流电感电压的保护方案，但是对区外双极短路和区内高阻接地故障存在误判现象。文献［11］利用正负极限流电感的电压之和检测故障，但是受限流电感值的影响大，限流电感较小时，保护可能会出现误动。文献［12-13］均提出基于直流电压变化率的保护方案，但是保护动作时间较长，受过渡电阻影响较大，无法实现柔性直流电网母线故障和线路故障的区分。文献［14］运用边界限流电感两侧的暂态能量比识别故障线路，耐受过渡电阻能力强且具有较好的选择性。文献［15］分析行波的时频相关性和差异性，提出单端行波保护方法，有效克服局部信息导致保护可靠性不高的缺陷，但是数量较多的高维矩阵匹配影响了保护速度，未考虑雷击干扰。

雷击干扰作为一种短时高频干扰，可能会使保护方案失效。目前国内外针对柔性直流电网雷击识别的研究较少。文献［16］基于小波变换，计算高频能量与低频能量比值有效识别雷击干扰，但是采样率较高。文献［17］利用差分电流幅值最大值构造雷击干扰判据，虽然能够准确区分线路故障和雷击干扰，但是整定方法较为复杂。

本文首先对柔性直流电网中故障电压行波进行时频分析，其次运用S 变换构造故障样本矩阵，通过主成分分析法（principal components analysis，PCA）降维处理，建立各线路的故障样本矩阵库。采用归一化互相关系数计算故障特征矩阵与故障样本矩阵的相似度，判别区内、区外故障。考虑雷击干扰对保护的影响，利用S 变换能谱矩阵，计算S 变换能量熵，由熵值变化识别雷击干扰。

1 柔性直流电网拓扑与行波特性分析

1.1 柔性直流电网拓扑

图1 为四端±500 kV 柔性直流电网某条直流线路模型，采用真双极拓扑结构［18］，其参数见附录A表A1。图1 中：L 为限流电感；P 为保护测量装置；MMC1 至MMC4 为换流站。区内故障F3包含正极接地短路、负极接地短路、双极短路；F4代表雷击干扰。区外故障分为F1、F2、F5，其中F1代表交流侧故障，F2代表母线故障，F5代表区外故障。本文规定从母线指向线路方向的行波为前行波，反之则为反行波。

图1 柔性直流电网拓扑Fig.1 Topology of flexible DC grid

1.2 行波特性分析

直流输电线路故障时由于正负极线路之间存在耦合，采用凯伦贝尔变换进行解耦，得到线模电压uF1、地模电压uF0、线模电流iF1、地模电流iF0，公式详见附录B 式（B1）。图1 中故障分量是由故障附加电源UF产生，RF为过渡电阻，计算线模电压反行波uf1、地模电压反行波uf0［19］为：

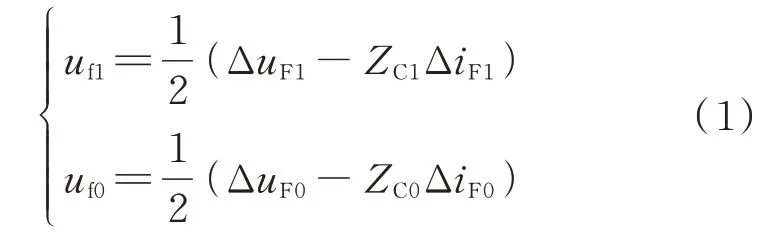
式中：ΔuF1、ΔiF1分别为线模电压和线模电流的故障分量（当前变量减去5 个周期前的稳态量）；ΔuF0、ΔiF0分别为地模电压和地模电流的故障分量；ZC0、ZC1分别为直流线路的地模波阻抗和线模波阻抗。

由于地模行波的色散比线模行波的色散严重，且双极短路故障时不存在地模行波，所以选择线模电压行波作为源信号。

根据故障网络边界条件［19］，采用凯伦贝尔变换，求出区内故障F3的初始线模电压幅值UR1，发生单极接地短路、双极短路的初始线模电压行波幅值为UR1，F3，S、UR1，F3，D（推导过程详见附录B）：

保护测量装置测得线模电压反行波UR1，P与xl处的初始线模电压幅值UR1的关系式如下：

2 故障行波时频特征分析

2.1 S 变换及能谱矩阵

2.1.1 S 变换

S 变换是一种可逆的局部时频分析方法，在连续小波变换和短时傅里叶变换基础上改进而来。相比连续小波变换，S 变换避免了基函数的选取，其高斯窗随频率自适应变化，解决了短时傅里叶变换时间分辨率和频率分辨率精度不能同时满足的问题。由于测量保护装置采集的是离散信号，S 变换的离散表达式如下［20］：

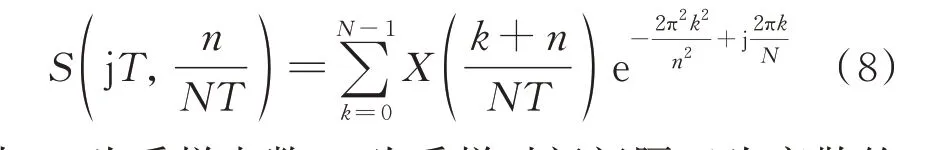
式中：N 为采样点数；T 为采样时间间隔；k 为离散的时间点，k=1，2，…，N-1；n 为频率采样点，n=1，2，…，N/2。

2.1.2 S 变换能谱矩阵

对采集的离散信号采用式（8）进行S 变换，得到（N/2+1）×N 复时频矩阵S，频率序号以行表示，离散时间点用列表示。对S 中各元素求模值，得到模时频矩阵D；对D 中第i 行第j 列即第i 个频率下第j个采样时刻的元素D（i，j）求平方，得到第i 个频率下第j 个采样时刻的信号能量谱密度E（i，j）为：

式中：fs为采样频率。

能谱矩阵可直观反映行波信号不同频段的能量随时间的分布或不同时间段上各频率的幅值。

2.2 区内故障分析

为模拟区内不同故障位置的正极短路故障，在线路上分别设置距离保护测量装置20、25、180 km的正极接地短路故障。通过行波网格图，对各故障点反行波传播过程进行分析，分析过程详见附录C。由分析可知，当直流输电线路发生区内故障，故障类型相同且故障位置较近时（如20、25 km），它们的线模电压反行波波形较相似，经S 变换构造的能谱矩阵可知，在时频空间的能量分布特征呈现较高的相似度，这是本文进行故障匹配的出发点。

2.3 区外故障分析

图1 中MMC1 换流站的保护测量装置对线路L1区内末端故障和正向区外近端故障最难区分，它们的行波时序特征相似，但由于区外故障电压反行波受到限流电感的平滑作用，有必要分析限流电感对线模电压反行波频域特性的影响。

由附录C 图C5 所示的线路远端区内、区外故障下函数G（jω）的幅频曲线，可分析得到频域幅值难以区分出区内远端高阻故障和区外故障，可能造成保护误动或拒动。

为解决此问题，本文分别计算区内、区外故障的线模电压反行波的S 变换能谱矩阵，绘制它们的能量谱密度图，如图2 所示。从图2 可看到，在故障发生后暂态时间内，区内故障的高频段幅值远大于区外故障，比单靠频域幅值区分故障的效果更优。去除S 变换在时间轴上开始一段和结束一段时间的边界效应，区内、区外故障在时频空间的能量分布特征呈现很大的差异，这是构造单端保护判据的依据。

图2 区内、区外单极接地短路故障能量谱密度图Fig.2 Energy spectral density diagram of internal and external single-phase-to-ground short-circuit fault

3 雷击干扰分析及识别判据

3.1 雷击干扰分析

雷击传输线路的概率非常低，且雷电流幅值一般不超过20 kA。雷电放电多为负极性脉冲波，约占总的雷电放电的75%～90%，本文仅针对正极线路的雷击干扰进行研究。雷电流模型采用1.2/50 μs的双指数模型，其函数表达式Is为［21］：

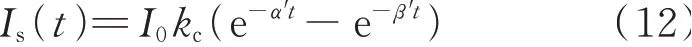
式中：I0为雷电流幅值；kc为波形校正系数；a＇、β＇分别为雷电流的波前、波尾衰减系数。

由雷电波频谱分析，雷电波主要频率集中在0～20 kHz［21］。根据香农定理，本文选择50 kHz 的采样频率，可采集到的最高频率为25 kHz，确保可采集到雷电波的主要频率。为对比雷击干扰和正极接地短路各自低频段与高频段的能量变化情况，将频段划分为0～1 kHz 低频段、1～25 kHz 高频段，在线路L1设置典型的雷击干扰、正极接地短路故障，通过S 变换对2 种故障的线模电压反行波进行分析，计算各频段2 ms 内的总能量。以0.5 ms 为时间间隔，计算各频段在各时间间隔内的能量与总能量的比值，雷击干扰和正极接地短路下各频段能量占比如表1 所示。

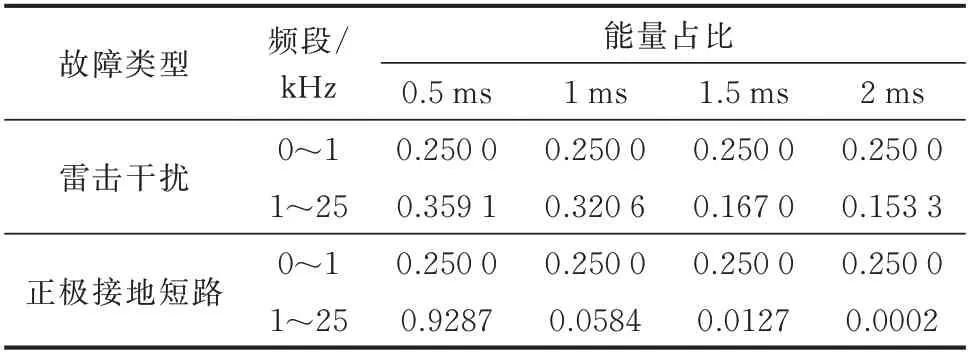
表1 雷击干扰和正极接地短路下各频段能量占比Table 1 Proportion of energy in each frequency band with lightning interference and positive grounding short circuit

由表1 可知，雷击干扰下0～1 kHz 低频段的能量分布均匀，1 kHz 以上的频段能量衰减缓慢。这是由于雷击干扰后不存在接地通路，电压行波的高频能量只能通过线路传播衰减，所以衰减缓慢。正极接地短路下0～1 kHz 低频段的能量分布均匀，但1 kHz 以上的频段能量衰减迅速，在1 ms 后基本衰减至0。这是由于正极接地短路存在接地通路，电压行波的高频能量快速消失。利用以上特性可有效区分雷击干扰和正极接地短路。

3.2 雷击干扰识别判据

由上节分析，雷击干扰、正极接地短路故障的行波信号在1～25 kHz 频段的能量衰减速度不同，即信号的紊乱程度不同。信息熵能够定量分析信号的紊乱程度［22］。引入S 变换能量熵，构建雷击干扰识别判据。计算故障时刻后第1 个采样时间窗的线模电压反行波，进行S 变换，根据2.1.2 节构造能谱矩阵E，求出第i 行对应频率的能量和Ei：

采样时间窗内的能量分布越复杂，WSEE熵值越大，反之熵值越小。随采样时间窗的移动，可得到随时间变化的能量熵。本文选择50 kHz 的采样频率、2 ms 的采样时间窗。分别设置在2 ms 时发生雷击干扰和正极接地短路，绘制对应的故障时刻前后2 ms 的S 变换能量熵曲线，如图3 所示。

图3 雷击干扰与正极接地短路下S 变换能量熵曲线Fig.3 Curves of S-transform energy entropy with lightning interference and positive grounding short circuit

利用最小二乘法，拟合出突变时刻后的S 变换能量熵曲线的斜率，由图3 可观察到正极接地短路对应曲线斜率绝对值大于1，而雷击干扰对应曲线斜率小于1。为了扩大两者差异，对曲线斜率求平方，作为衰减速率R，从而建立雷击干扰识别判据：

式中：Rset为雷击干扰识别阈值。

Rset根据区内正极接地短路故障时可能出现的衰减速率最小值Rmin进行整定，Rset=Rmin/Krel，其中可靠系数Krel的取值范围为1.2～1.4。

当判据式（15）成立时，判断为雷击干扰，否则判断为接地故障。

4 基于S 变换能谱矩阵相似度的单端保护

4.1 单端保护特征矩阵构造

为降低高维矩阵的维数，采用PCA，它是一种多元统计分析方法，原理是分析主成分，去除维度之间的相关性，使线性相关的向量组变成线性无关的向量组，将高维向量映射到低维空间。当直流输电线路发生故障时，采用PCA，对能谱矩阵E 去中心化处理，求出协方差矩阵C 及其特征值矩阵λ 与特征向量矩阵μ。主成分矩阵P 为能谱矩阵E 与特征向量矩阵μ 的乘积：

根据大量仿真实验，z 取2 时累计贡献率Y 可达到95%以上，所以提取主成分矩阵P 的前2 列作为故障特征矩阵Ef。PCA 处理不仅能减少故障样本矩阵库的存储空间，而且明显缩短了故障特征矩阵与样本库中各故障样本矩阵的匹配时间。

4.2 故障样本矩阵库构建

针对图1 所示的柔性直流电网模型，以全长为200 km 的L1线路为例，从线路首端0 km 开始，每隔10 km 设置一个故障点，故障点故障类型包含正极接地短路、负极接地短路、双极短路，计算故障时刻后第1 个采样时间窗的线模电压反行波，分别计算各故障位置点的正极能谱矩阵EP、负极能谱矩阵EN、双极能谱矩阵ED，建立该线路在3 种故障类型下的故障样本矩阵库，双极短路故障样本矩阵库包含20 个故障样本矩阵（双极金属性短路）；正极接地短路、负极接地短路故障样本矩阵库分别包含40 个故障样本矩阵（通过大量仿真选择间隔10 km，过渡电阻分别为0 Ω 和150 Ω，取值依据见附录D）。

4.3 基于归一化互相关系数的矩阵相似度计算

借助图像匹配的相似度计算原理，引入归一化互相关系数（normalized cross-correlation coefficient，NCC），计算故障特征矩阵Ef与第s 个故障样本矩阵Es之间的相似度，Ef与Es均为M×N 矩阵。运用归一化互相关系数，计算得到故障特征矩阵Ef与故障样本矩阵Es之间的相似度ρfs如式（18）［24］所示。

归一化互相关系数在［-1，1］内，衡量2 个矩阵之间的相似性，ρfs值越接近于1，两者越相似。

4.4 保护启动判据

为了避免保护因电压波动而造成频繁误动，采用S 变换能量熵变化量，构建快速启动判据。由图3可看出，线路正常运行时，S 变换能量熵变化量稳定在1 以下；线路故障时，S 变换能量熵变化量大于1。以检测到第1 个S 变换能量熵突变值的时刻作为故障发生时刻，保护装置启动。

构造S 变换能量熵变化量ΔWSEE(m)为：

式中：Δset为保护启动阈值，取值为2。

熵值大小只与信号的波动程度有关，与信号幅值大小无关，采用S 变换能量熵变化量作为启动判据，既具有较强的耐噪声能力，又能在高阻故障情况下使保护可靠启动。

4.5 故障极识别

柔性电网模型为真双极结构。当发生正极故障时，负极电压在额定电压附近波动，会产生大小为负的地模电压；当发生负极故障时，产生大小为正的地模电压；当发生双极短路故障时，正极电压、负极电压的变化趋势相同，理论上地模电压为零。因此，通过地模电压进行故障极识别。计算地模电压uF0在采样时间窗的地模电压总和A 为：

建立故障极识别判据如下：

式中：Aset为故障选极的阈值，经过大量仿真选择设置为10。

4.6 单端行波保护判据

根据故障极判据得到故障类型，将故障特征矩阵与对应故障类型的各故障样本矩阵一一进行相似度计算，取其中最大相似度作为线路故障度F，柔性直流线路的单端保护判据如下：

式中：Fset为保护阈值。

Fset根据区内故障下可能出现的相似度最小值Fmin进行整定，Fset=Fmin/Krel，可靠系数Krel取值范围为1.2～1.4。

4.7 柔性直流电网单端保护算法

1）针对每条线路，建立该线路的3 种故障类型的故障样本矩阵库。

2）在测量保护安装处实时计算线模电压反行波uf1、地模电压uF0，计算线模电压反行波的S 变换能量熵变化量ΔWSEE，将它与保护启动阈值比较，判断保护是否启动。

3）当保护启动后，计算地模电压uF0之和A，判断故障类型。

4）如果判断为单极接地短路，则计算衰减速率R，当R 满足雷击干扰识别判据时，则判断为雷击干扰，否则为单极接地短路。

5）若非雷击干扰，则计算故障特征矩阵Ef，计算Ef与对应故障类型的故障样本矩阵库中第s 个样本矩阵Es之间的相似度，取其中相似度最大值为线路故障度F。若F 满足保护判据，则判断为区内故障，保护动作，否则，保护复归。

基于S 能谱矩阵相似度的单端保护算法流程图如图4 所示。

图4 基于S 变换能谱矩阵相似度的单端保护算法流程图Fig.4 Flow chart of single-end protection algorithm based on similarity of S-transform energy spectrum matrix

5 仿真分析

参考中国张北柔性直流电网系统拓扑及有关参数，利用PSCAD/EMTDC 软件搭建±500 kV 四端柔性直流电网模型。除线路L4长度为50 km，其余线路均为200 km。采样频率为50 kHz，设柔性直流电网在2.0 s 时发生故障，故障持续0.1s，选取2 ms的采样时间窗，为避免S 变换的边界效应及线路对高频分量衰减的影响，剔除能量谱矩阵中0～0.2 ms，1.4～2.0 ms 的数据，去除0 Hz 和500 Hz 的低频分量。分别设置不同故障类型的区内、区外故障，数据中包含一定的噪声。

5.1 区内故障

为检验柔性直流电网发生区内故障时保护方案是否存在死区，在线路L1的首端、中端、末端分别设置故障，考虑到最不利情况为2 个相邻故障所在位置的中间点发生故障，分别设置5、105、195 km 处正极接地短路、负极接地短路、双极短路故障。过渡电阻分别为0.01 Ω 和350 Ω，添加30 dB 高斯白噪声进行对比，仿真结果如表3 所示。

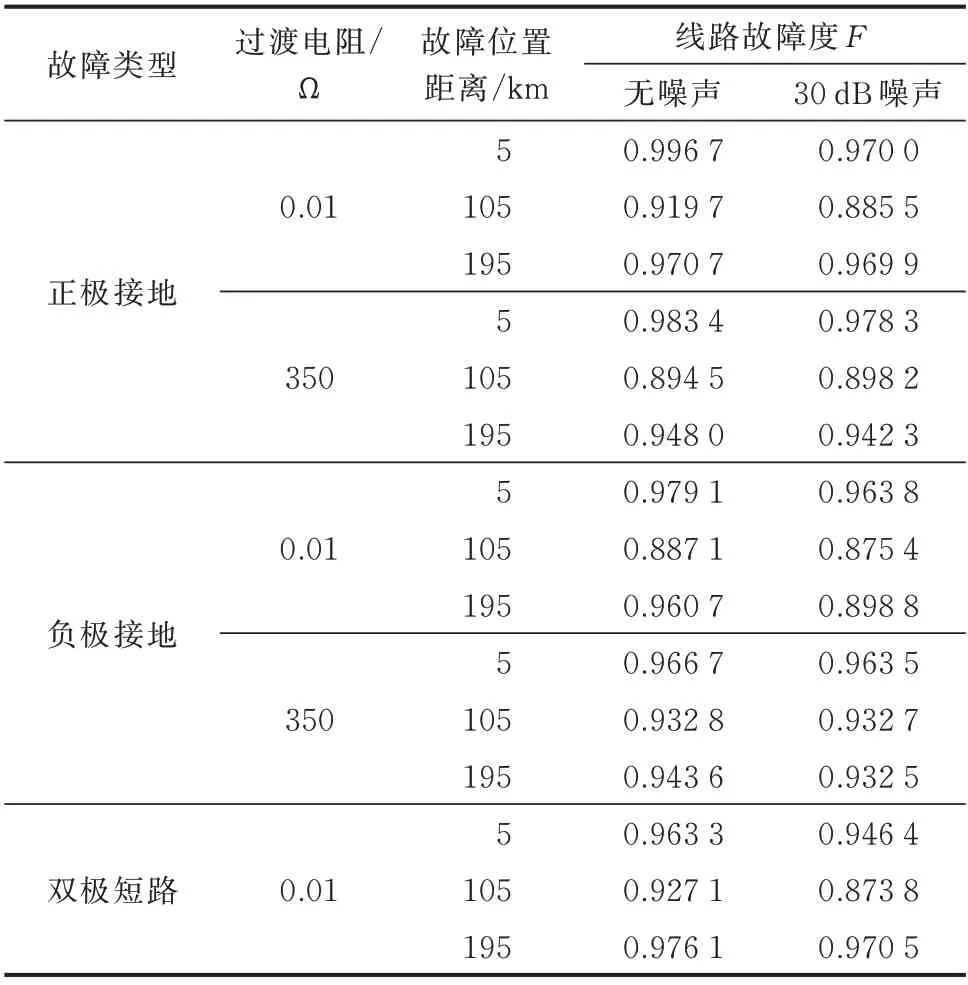
表3 线路L1区内故障的仿真结果Table 3 Simulation results of internal fault on line L1

如表3 所示，该保护方案能够有效识别出区内不同故障位置的故障，不存在保护死区。在线路末端高阻350 Ω 和30 dB 噪声干扰的综合作用下仍可准确识别区内故障。在最不利情况即线路中点105 km处发生双极短路并含信噪比为30 dB 的噪声时，故障度0.873 8 为最小。为保证保护的可靠性，设置可靠系数为1.25，保护阈值Fset=0.873 8/1.25=0.7。

5.2 区外故障

为得到区外故障最不利情况，所有区外接地短路均设为金属性接地短路。对于区外直流输电线路故障，同样考虑添加30 dB 高斯白噪声进行对比，得到线路区外故障仿真结果，如表4 所示。

如表4 可见，区外故障的故障度最高为0.277 2，大多数相似度在0 附近，保护可靠不误动。区外母线故障、区外交流侧故障保护均能可靠不误动。保护算法受限流电感值的影响很小，在100～300 mH的限流电感情况下均能可靠动作。本文所提方法还与文献［25-26］保护方法进行了性能对比，在耐受过渡电阻、识别雷击干扰及保护动作时间上具有明显优势，仿真结果见附录E。

表4 输电线路L1区外故障的仿真结果Table 4 Simulation results of external fault of line L1

5.3 雷击干扰

为检验雷击干扰判据能否可靠区分雷击干扰和正极接地短路，在线路L1的首端、中端、末端分别设置故障，正极接地短路过渡电阻分别设置为0.01 Ω和350 Ω。仿真结果如附录F 表F1 所示。考虑故障后高频分量在线路上衰减，最不利的情况为L1线路中点100 km 处发生经350 Ω 过渡电阻的正极接地短路，L3线路衰减速率为1.244 1（最低）。为保证保护的可靠性，设置可靠系数为1.25，雷击干扰识别阈值Rset=1.244 1/1.25≈1。

附录F 表F2 为不同雷击位置和雷电流幅值下的仿真结果，表F3 为雷电流波形对雷击干扰判据影响的仿真结果，均能可靠识别雷击干扰。表F4 限流电感对雷击干扰判据影响的仿真结果表明，雷击干扰判据受到限流电感影响很小，可耐受100～300 mH 的限流电感。

5.4 保护动作速度和计算耗时分析

为检验算法是否满足柔性直流保护对速动性的苛刻要求，对本文算法的耗时进行统计。计算机配置：i5-3230M CPU 型，主频2.6 GHz，内存4 GB。

对未经PCA 和经过PCA 处理的匹配过程分别进行统计，未经PCA 和经过PCA 处理的平均每次匹配时间分别为0.9 ms、0.035 ms，总匹配时间分别为36 ms、1.4 ms。可见，经过PCA 处理大大缩短了匹配时间，能够满足速动性要求。

在保护启动后一个时间窗后，PCA 处理时间t1约为0.6 ms；故障匹配时间t2为1.4 ms；考虑光电转换延迟、测量延迟、启动延迟等均为微秒级，总延迟时间t3约为0.1 ms。本保护方案计算时间Tc=t1+t2+t3=2.1 ms。保护启动后经1 个时间窗2 ms 数据采集，加上计算时间Tc，本保护方案总处理时间为4.1 ms，小于5 ms，满足柔性直流电网保护的速动性要求。

6 结语

针对柔性直流电网，本文通过时频变换分析电压反行波在区内和区外故障的特性，采用S 变换建立能谱矩阵，根据矩阵的相似度，提出一种柔性直流线路单端保护方案，得到如下结论：

1）本保护方案只需利用单端行波，采用S 变换构造能谱矩阵，能够区分出区内、区外故障，对含有一定噪声干扰的测量数据具有良好的耐受能力，不会出现保护误动，并具有一定的抗过渡电阻能力。

2）本保护方案速动性高，通过PCA 减少了96%存储空间，使故障特征矩阵与故障样本矩阵库中所有样本矩阵的总匹配时间缩短至1.4 ms，能够满足柔性直流保护2～5 ms 动作的苛刻要求。

3）考虑雷击干扰对本保护的影响，可确保雷击干扰时保护可靠不动作，提高了保护的可靠性。

本保护方案尚未考虑雷击故障对保护算法的影响，故障样本矩阵库中的样本数较多。如何识别雷击故障并减少样本数是进一步研究的方向。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。