基于统一潮流大数据的综合能源系统薄弱点辨识方法
王 波,王红霞,朱丹蕾,董旭柱,马恒瑞
(1. 武汉大学电气与自动化学院,湖北省 武汉市 430072;2. 长江勘测规划设计研究有限责任公司,湖北省 武汉市 430010;3. 青海大学新能源光伏产业研究中心,青海省 西宁市 810016)
0 引言
随着化石能源日益稀缺和环境逐渐恶化,通过综合能源系统(integrated energy system,IES)实现对电、热、气等多种能源的统一规划设计和运行优化,并提高能源综合利用效率,已经成为人类社会能源领域变革的必由之路[1-2]。但是,IES 中多种能源系统紧密耦合,任一子系统内的扰动都可能通过耦合元件扩散到其他子系统,从而引起整个综合能源系统状态的变化,且越薄弱的环节,其异常对系统的状态影响越大。因此,快速识别IES 中对系统状态影响较大的薄弱环节,并对其进行必要的监控,具有重要的理论和应用研究价值。
针对单一的电力系统,文献[3]基于系统内节点和边的关联关系,采用功率变化度评估节点功率变化对系统的影响,并基于此进行薄弱环节识别。文献[4]同时考虑潮流状态和拓扑结构,通过对负载潮流熵、支路开断熵以及加权综合熵指标的排序筛选实现支路脆弱性辨识。但以上方法难以应对IES 节点众多、关联关系复杂的情况。而IES 的薄弱环节辨识仍处于初步探索阶段:文献[5]考虑综合能源系统中孤岛存在的可能性,构建了包含电-气-热的相互依存网络,并使用树核度指标进行脆弱性评估,但其仅考虑了IES 的静态结构特性,对动态交互影响特性考虑不足;文献[6]基于灵敏度指标分析电网节点注入功率对燃气压力的影响,实现电-气耦合IES的脆弱性分析,但面对大型或含更多能源的耦合系统时,该方法因潮流模型复杂,难以实现快速响应。
随机矩阵理论(random matrix theory,RMT)是一种基于统计的大数据分析方法,目前已被应用到电力系统的静态和暂态稳定性分析[7-8]、输变电设备的状态评估[9]以及智能电网的窃电检测[10]等多个领域。文献[11]基于随机矩阵理论和熵理论,建立了电力系统薄弱点辨识模型,并验证了随机矩阵在电力系统薄弱环节识别中的有效性。文献[12]在此基础上,结合多种极限谱分布函数,提出了改进的薄弱点辨识方法,避免了利用单一指标进行分析带来的误差。可见,随机矩阵理论能够将复杂系统的特性映射至数据变化中,从数据的关联和交互影响特性中提取薄弱点信息,对难以建模的复杂系统具有良好的适应性。而IES 中各异质子网络相互耦合,多种能量形式相互转换,多个环节动态交互,难以进行有效建模,更难以基于统一标准进行薄弱点辨识。因此,采用随机矩阵理论进行IES 的薄弱性辨识,具有一定的优势。
基于此,本文提出一种基于随机矩阵理论的电-热-气IES 薄弱点辨识方法。首先,分别建立电、热、气系统的单个潮流模型,并基于其耦合关系建立IES 统一潮流模型;然后,利用统一潮流模型中可表征IES 状态的不平衡量初值构建高维状态矩阵,并基于M-P 律、圆环律分析系统状态变化与不平衡量数据波动的关系;最后,计算平均谱半径和状态矩阵的最大特征值,结合熵理论计算节点薄弱评价值,并基于评价值排序进行薄弱点辨识。
1 IES 统一潮流模型
1.1 电-热-气IES
如图1 所示,含电、热、气的IES 由电力、热力、天然气系统及耦合环节组成[13]。耦合环节包括热电联产(combined heat and power,CHP)机组、燃气锅炉、电锅炉等设备,可实现不同能源之间的转换。

图1 IES 结构Fig.1 Structure of IES
1.2 电力系统模型
IES 中电力系统的节点功率表达式为:
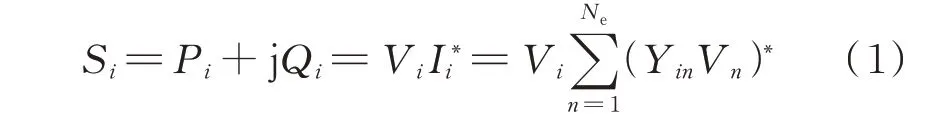
式中:Ne为电力网节点总数;Vi为节点i 的电压;Ii为节点i 的电流;Yin为节点导纳矩阵Y 第i 行第n 列元素;Si为节点i 的复功率;Pi为节点i 的有功功率;Qi为节点i 的无功功率。
1.3 热力系统模型
1)水力系统模型
水力系统模型中节点满足流量连续性方程[14],即节点所有注入流量之和与该节点流出流量相等:

式中:Bh为水力系统回路-支路关联矩阵;hf为压头损失向量。

1.4 天然气系统模型
天然气模型与热力网络水力模型相似[15],满足流量连续性方程:

式中:Kg为管道阻力系数矩阵;k 为指数,与天然气系统压力水平有关,本文k 取2。
1.5 耦合元件模型
CHP 机组[16]利用燃气的高品位能量发电、低品位能量供热和供冷,使得用能效率达80%以上。含CHP 机组的耦合环节为:


1.6 统一潮流模型构建
综合上述对电力、热力和天然气系统及耦合环节的模型分析,构建IES 模型如式(12)所示。
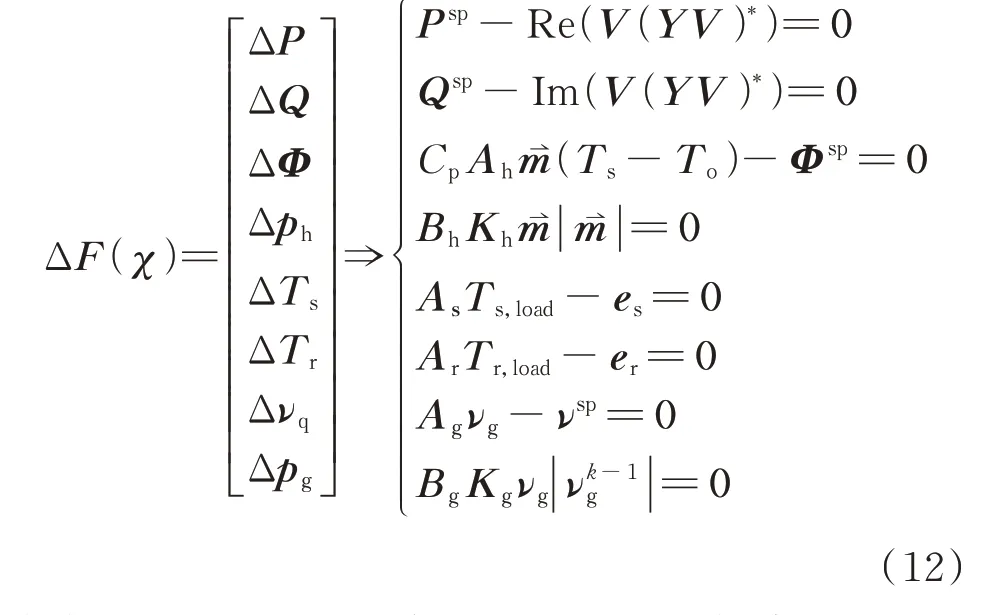
式中:ΔF(χ)为不平衡量;ΔP 和ΔQ 分别为电力系统的有功功率和无功功率偏差向量;ΔΦ、Δph、ΔTs、ΔTr分别为热力系统的热功率、回路压降、供热温度、回热温度偏差向量;Δνq和Δpg分别为天然气系统的管道流量和回路压降偏差向量;Psp、Qsp、Φsp、νsp分别为相应变量的给定值;V 为电力系统节点电压向量;Ts和To分别为热力系统各负荷节点的供热和输出温度向量;Ts,load和Tr,load分别为热力系统热负荷节点的供热温度和回热温度向量;As和Ar分别为与供热、回热网络结构和管道流量有关的矩阵;es和er分别与供热、回热温度有关的列向量,计算方法详见文献[17];χ=[θ,| |V ,m⇀,Ts,Tr,νg]T,为IES 的状态变量,其中Tr为热力系统回热温度向量,θ 为电力系统节点电压相角向量。
利用牛顿拉夫逊方法,可同时求解IES 的不平衡量和状态变量:)
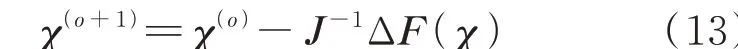
式中:o 为迭代次数;J 为雅可比矩阵,其计算方法详见文献[18]。
2 随机矩阵理论
随机矩阵理论是面向高维数据矩阵的统计分析方法,主要包括渐近谱分布理论、自由概率理论、副本方法等[19]。其中,渐近谱分布理论主要分析经验谱分布函数在一定条件下的特殊收敛性质,已在无线电、金融、电力系统等领域得到了较好的应用。
经验谱分布函数是矩阵常用的概念,对于一个N×M 的矩阵XT,其样本协方差的特征值为λj,XT( j=1,2,…,N )。若所有特征值都是实数,则定义经验谱分布函数GX(x)为:
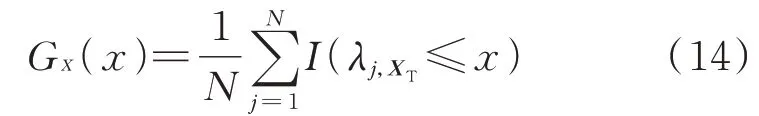
式中:I(·)为示性函数;x 为自变量。
当矩阵XT的维数趋于无穷且矩阵中的元素符合独立同分布时,其经验谱分布将收敛至M-P 律和圆环律[20-21]。
本章首先对随机矩阵理论中的M-P 律、圆环律以及平均谱半径等概念进行介绍,然后基于此对其在IES 中的应用基础进行说明。
2.1 M-P 律
对于N×M 非Hermitian 矩阵XT,其样本协方差矩阵为Ψ=XTXTT/N。 当矩阵的维度满足N →∞和M →∞,d=N M ∈(0,1],且矩阵中的元素符合独立同分布条件,并满足均值μ=0、方差σ2<∞时,其协方差矩阵的经验谱分布收敛于M-P律,密度函数fESD(λ)表示为:

当矩阵中元素符合独立同分布条件时,其经验谱分布函数与M-P 律的契合度高,特征值均分布在[a,b]之间;反之,当其偏离独立同分布条件时,经验谱分布函数偏离M-P 律,且出现大于b 的特征值。
2.2 圆环律

该定理表明,当矩阵中元素符合独立同分布条件时,Z 的特征值分布在复平面上内环半径为(1-d)O2、外环半径为1 的圆环内。
平均谱半径(mean spectral radius,MSR)可用来反映特征值的统计特性,其为复平面上所有特征值距离圆心的平均值。当矩阵中元素均符合独立同分布条件时,MSR 处于内外环半径之间;反之,当其偏离独立同分布条件时,MSR 跌落至内环半径以

2.3 随机矩阵理论在IES 中的应用基础分析
当IES 处于平衡稳定状态时,各节点的量测数据(如电力系统中的电压数据、热力系统管道流量、天然气系统管道流量等)在某一固定值附近,仅仅由于测量误差、小扰动或外界的干扰而有小的浮动,可用高斯白噪声模拟,此时系统的量测数据符合独立同分布条件,因此符合随机矩阵理论的相关定理,即状态矩阵的特征值均分布在[a,b]内,MSR 在内外环之间;反之,当IES 出现负荷突变、故障等大扰动时,部分节点的量测数据会出现相应的变化,数据之间存在关联性,不再满足独立同分布条件,故不再满足随机矩阵理论的相关定理,即状态矩阵出现大于b 的特征值,MSR 跌落至内环半径以内,且所受扰动的程度越大,偏离随机矩阵理论的程度越大。
综上,IES 中的运行数据能够表征其运行状态,且满足采用随机矩阵理论分析数据的条件,具有进行薄弱点识别的基础。
3 IES 薄弱点辨识方法
3.1 IES 薄弱点概念
IES 中,单个能源子系统内某一环节一旦发生扰动,其冲击会通过耦合元件扩散到整个多能系统,并引起相应的变化,这是一种使系统“薄弱”的现象,即薄弱是指当系统某一环节发生改变从而引起整个系统状态变化的能力[22-23]。不同节点发生同一异常(如故障或扰动等)时,会引起整个系统状态的不同程度变化。越薄弱的节点,其发生异常时对整个系统的状态影响越大。在同一个IES 中,节点的薄弱性是相对的,即分别对每个节点求薄弱性,然后根据薄弱性指标值的排序确定系统中各环节的相对薄弱性。
本文首先用不同子系统中的量测数据构造高维状态矩阵,然后在不同节点设置相同类型的异常,并分析相应条件下系统的状态变化情况。越薄弱的节点,其异常引起系统的状态变化越明显,评估某一节点i 的薄弱性时,基本步骤如下:
1)将节点i 设置为异常状态;
2)建立IES 统一潮流模型,采集ΔF(χ)的历史数据和实时数据,利用实时分离窗技术构建状态矩阵XT;
3)对XT进行标准化预处理;
4)基于M-P 律和圆环律,分析高维数据矩阵的特征值分布随系统状态的变化过程,对IES 进行异常状态识别;
5)分别对每个节点构建增广矩阵,并计算其在当前异常情况下的状态变化程度;结合熵理论计算薄弱评价值W,并基于W 评估异常情况对整个系统的状态影响,W 越大表示该节点越薄弱。
3.2 IES 随机矩阵构建
本文首先搭建IES,然后模拟IES 中的电力系统计量装置、热力系统热力表计、天然气系统气表计等量测装置,对电、热、气系统能源运行数据进行测量,在仿真中采用潮流计算结果,并基于此构建大数据矩阵,实现其薄弱点识别。根据2.3 节中分析,本文选取IES 统一潮流模型下的不平衡量初值ΔF(0)(χ)构建随机矩阵。不平衡量ΔF(χ)包含电力系统的有功功率、无功功率,热力系统的管道流量、节点供热、回热温度,天然气系统的管道流量等关于节点和支路的多种重要信息。由于IES 潮流模型复杂、迭代次数多,因此选取ΔF(χ)在第0 次迭代的初值ΔF(0)(χ)构建随机矩阵,无须进行潮流模型计算,避免了对IES 进行建模的过程,大大缩短了运行时间。
确定随机矩阵的数据选取后,在某一采样时刻t,N 个测量数据x1,t,x2,t,…,xN,t可构成一个列向量xt:
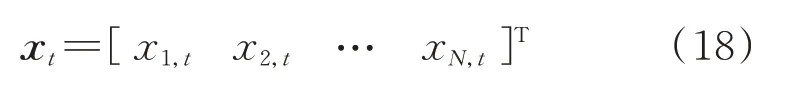
本文基于连续潮流法[7-8]对IES 历史数据进行模拟构建。首先令系统运行在稳定状态,然后,在某一时刻给定一个扰动,让系统从稳定状态过渡到不稳定的状态。随着时刻的增加,系统潮流状态的数据不断被刷新。本文把这些大量历史数据和实时数据保留下来,添加高斯白噪声,来模拟IES 实际运行获得的数据构建矩阵X:
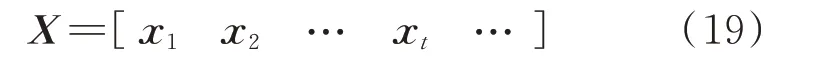
为了充分考虑矩阵X 中包含大量的历史样本数据,本文采用实时分离窗技术[12]得到N×M 矩阵XT,其中,N 表示IES 的节点数,M 表示分离窗的宽度,本文根据d=0.75 选择分离窗的宽度。

采集第t 时刻及该时刻之前长度为M-1 的数据,共同构建随机矩阵。
3.3 IES 随机矩阵预处理
对于原始矩阵XT,首先把所有元素进行标准化处理,即去量纲化和对数值进行归一化,使各个指标具有可比性,归一化后的XT表示为X̂。
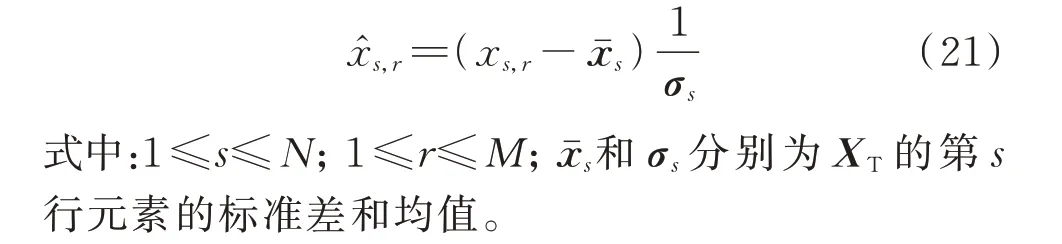
3.4 IES 异常状态识别
在与M-P 律进行对比时,需计算样本协方差矩阵的特征值,并依据下式对特征值分布进行非参数估计[24]:

式中:zs=[ zs,1,zs,2,…,zs,N],为Z 的行向量;σzs为zs的标准差;z͂s为zs标准化后的向量。
将z͂s的特征值画在复平面上,若所有特征值都分布在式(16)所示的内外环之间,则系统没有异常;若仅有极少特征值落在圆环外,则认为是统计误差。反之,当出现数量可观的特征值落在内环时,可判断系统出现异常。基于MSR 可对复平面上的特征值进行统计特性分析,MSR 跌落程度越大,说明系统偏离稳定性程度越大,并对系统的影响也越大。
3.5 IES 薄弱点辨识

增广矩阵使被复制数据在矩阵中的权重增大,MSR 结果偏向于该节点的数据特征,进而分析该节

式中:μi为节点i 的MSR 概率化数值。
计算第i 个节点的评价值Wi:

由式(15)及2.3 节分析可得,当IES 处于平稳状态时,其状态矩阵的特征值将分布在[a,b]范围内,最大特征值接近于b;反之,当IES 处于异常状态时,其状态矩阵的特征值分布将会超出[a,b]范围,且IES 偏离正常状态的程度越大,最大的特征值偏离b的程度也越大。
Wi表征了节点i 处异常对系统的影响程度,Wi值越大,则对应节点状态变化对系统状态影响越大,节点薄弱程也度越大。

4 算例仿真
4.1 算例系统潮流模型
本文以文献[18]的实际IES 为基础,对其进行改造,构建了IES 算例,网络拓扑如图2 所示。图中:CHP1 和CHP2 分别表示第1 台和第2 台CHP 机组;EB1 至EB12、HB1 至HB11、GB1 至GB6 分别表示电、热和气节点。该算例系统的应用场景为:电力系统为并网模式,EB13 连接大电网,是电力平衡节点,EB11、EB12 为光伏节点。热力系统以连接CHP2 的HB13 作为平衡节点,HB12 和HB13 为热源节点。天然气系统中,GB1 连接天然气站作为平衡节点,GB5 和GB6 除自身负荷外,还需为电力和热力系统提供CHP 机组的耗气量。算例系统参数详见附录A。
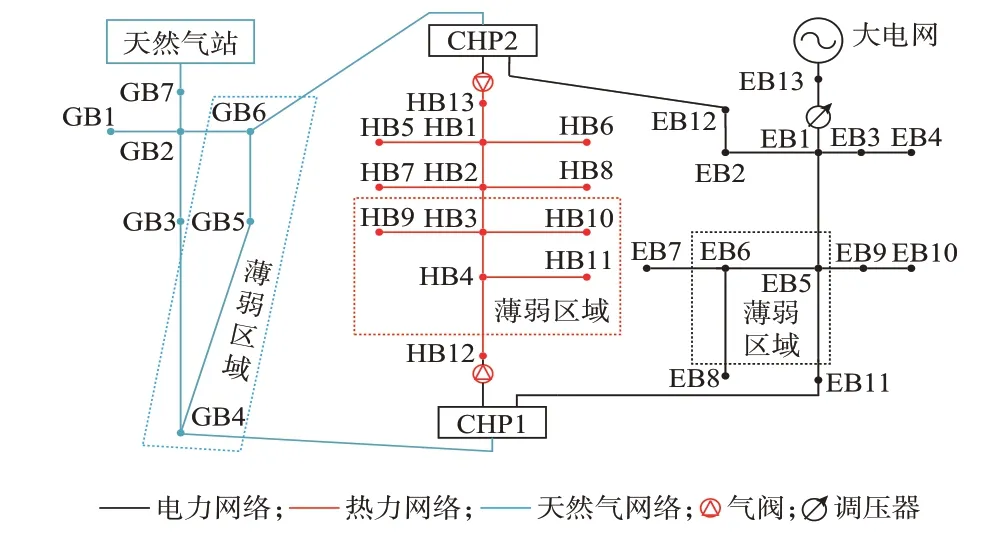
图2 IES 模型Fig.2 IES model
经过10 次迭代,IES 统一潮流计算完成,计算结果如附录B 所示。由附录B 可知,电力系统各节点电压均在0.94~1.06 p.u. 范围之内,没有越限。EB10 负荷较大且离电源较远,因此其电压最低。热力系统有3 个热源,供热温度最低的是热力系统拓扑结构中间的HB7。天然气系统GB4、GB5 的耗气量由2 台CHP 机组决定。
4.2 异常状态识别
应用实时分离窗技术,在系统中某节点设置逐渐增加的负荷,并基于系统不同状态下不平衡量初值来观察M-P 律和圆环律。
如图3 所示,系统处于初始的正常稳定状态时,核密度与M-P 律契合度较高,状态矩阵的最大特征值接近b 但小于b;随着系统中负荷的逐渐增加,核密度与M-P 律的契合度逐渐下降,状态矩阵的最大特征值大于b,且系统状态越不稳定,最大特征值偏离b 的程度越大。

图3 系统不同状态下的M-P 律Fig.3 M-P law of system under different states
如图4 所示,系统处于初始的正常稳定状态时,复平面上的特征值分布在内环与外环之间,MSR 大于内环半径;系统负荷开始逐渐增加时,复平面上的特征值逐渐向圆心聚拢,MSR 开始跌落至内环半径以内,且系统不稳定的程度越高,复平面上的特征值向圆心聚拢的程度越大,MSR 越小。

图4 系统不同状态下的圆环律Fig.4 Ring law of system in different states
可见,M-P 律和圆环律均能表征IES 系统在扰动下的状态变化,用其构造节点的薄弱性指标具有可行性。
4.3 算例薄弱点辨识
基于所提指标,对IES 薄弱点进行辨识。在薄弱性评估过程中,本文在每个节点均设置相同增长率的负荷,并结合熵理论计算Wi值,按薄弱程度排序得到表1。表1 中Wi值反映了各节点异常对系统的影响程度,Wi值越大表明对系统的影响越大,系统状态越不稳定,则对应节点越薄弱。电力系统与外部大电网相连,系统内电功率的波动由大电网平衡,天然气系统同理;热力系统仅由CHP 机组提供热功率,系统内波动仅通过自身平衡,一旦热力节点发生异常,其余节点状态容易改变,Wi值较大,因此热力节点相对电力节点、天然气节点更薄弱。
结合表1 中的各节点电压和IES 拓扑结构(如
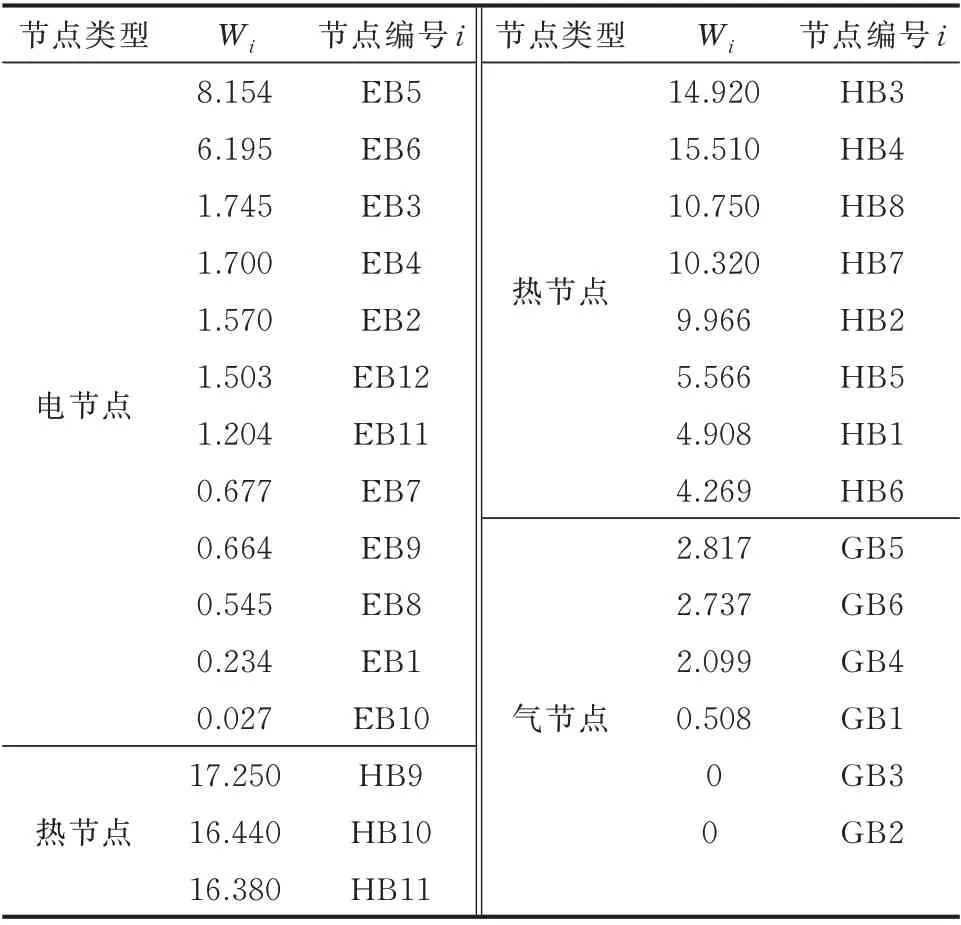
表1 IES 薄弱节点辨识结果Table 1 Identification results of weak nodes in IES

为进一步验证所提方法的有效性,本文将IES中的电力系统独立出来,并对独立的电力系统节点薄弱性进行分析,在每个节点上设置的增长负荷与上文相同,薄弱性评估结果如表2 所示。
由表2 可知,靠近大电网的节点由于电力系统的调节能力较强,其薄弱性较低,远离大电网、连接节点多的节点更薄弱,与实际情况相符合。同时,单独的电力系统中节点的薄弱性与电-气-热耦合的IES 中电气节点的薄弱性有差别,这进一步说明了IES 薄弱环节受不同能量系统耦合的影响,传统适用于电力系统的薄弱性评估方法无法适用于IES。

表2 电力系统薄弱节点辨识结果Table 2 Identification results of weak nodes in power system
5 结语
本文以IES 统一潮流模型下的不平衡量初值为基础数据,提出了基于随机矩阵理论的IES 薄弱点辨识方法。随机矩阵理论能将IES 的状态映射到其运行数据变化中。基于此,本文考虑IES 中各节点的差异性,将平均谱半径、状态矩阵的最大特征值与熵理论相结合,构造了薄弱性评估指标,其从多个角度反映了节点异常对IES 状态的影响程度,并通过对各节点的薄弱性值进行排序实现系统的节点相对薄弱性分析。所提方法以数据驱动方式分析系统运行状态,并将系统状态映射至节点薄弱性中,避免了对复杂系统的建模,为综合能源薄弱环节辨识提供了新思路。未来,将进一步考虑IES 中各节点的用能需求,对薄弱性进行精细化的分析研究。
本论文受到国家自然科学基金(51907096)资助,特此致谢。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。

