计及相关性影响的增强台风灾害下配电网韧性灵活性资源规划

马丽叶，王海锋，卢志刚，郑聃杰

（1. 电力电子节能与传动控制河北省重点实验室（燕山大学），河北省 秦皇岛市 066004；2. 燕山大学电气工程学院，河北省 秦皇岛市 066004；3. 莆田市供电服务有限公司仙游分公司，福建省 莆田市 351200）

0 引言

近年来随着全球气候变化加剧，由极端灾害引起的大规模停电事件频发，造成了严重的经济损失［1］。以强台风为例，通常会造成杆塔倒塌和配电线路断裂导致负荷停电，影响正常的生产生活。灵活性资源可以在故障期间尽可能多地为故障区域内的失电负荷提供供电支撑，从而减少系统失负荷量，提升配电网韧性［2-3］。因此，针对灵活性资源的韧性规划具有重要意义。

目前，已有学者对如何提升系统韧性进行了探讨。在台风灾害下的配电网故障率建模方面，文献［4］综合考虑故障发生频率、停电时长和缺供电量等指标，对配电网风险等级进行划分，并与天气因素进行关联分析，但未考虑提升韧性的措施。文献［5］采用5 种机器学习算法建立了配电网的杆塔受损空间分布预测模型，实现了对预测结果可视化，但未考虑杆塔之间连接的相关性。文献［6］建立了数据-机理联合驱动的台风配电网故障率模型，同时考虑台风和暴雨灾害，但文中缺少对韧性与经济性之间的主次划分。文献［7］根据气象地理特征建立了自然灾害电网故障率时空预警框架，对台风和暴雨灾害预警具有自适应能力，但模型过度依赖于历史数据，未与机理模型相结合。

在台风灾前部署和规划方面，文献［8］通过对配电线路的加固，考虑了台风行驶轨迹和风速不确定性，但线路加固方法成本高，且线路故障具有不确定性导致费用损失率高。文献［9］以最小化加固成本、储能成本、切负荷成本为目标建立鲁棒优化模型，提高了对关键负荷的供电能力，但仅考虑了单一灵活性资源配置措施。文献［10］提出一种内外双层循环算法对综合能源系统韧性进行优化，但韧性提升措施仅考虑了线路加固对失负荷成本的影响，未考虑综合成本。文献［11］计及分布式电源出力的不确定性，建立了防御-攻击-防御（defender-attackerdefender，DAD）3 层优化框架进行韧性规划，但文中未考虑极端天气对风电、光伏出力的影响。

综上所述，针对传统配电网故障率模型未计及相关性影响、气象和地理信息刻画难度高以及在韧性规划时规划对象较为单一，未考虑韧性与经济性主次关系的问题，本文采用PageRank 算法构建了计及相关性影响的台风灾害下的配电网故障率模型；在该模型中引入信息扰动系数μ，通过径向基函数（radical basis function，RBF）神经网络建立非线性映射，形成代理模型；提出了一种新的韧性量化指标，该指标可体现单个负荷以及灵活性资源对电网韧性的影响，以该指标最优和经济性最大化为上下层目标函数，构建了台风灾害下的灵活性资源选址定容双层规划模型，通过协调规划，使得配电网在韧性提升的同时实现了经济性最优。

1 韧性规划概述与思路框架

目前，对电力系统韧性的研究仍处于起步阶段。电力系统韧性可被定义为电网在极端灾害或者人为破坏的影响下，通过主动措施保障重要负荷供电，并快速恢复到正常运行状态下的能力。韧性提升的方法主要通过灾前预警、灾前规划和灾后调度来实现。灾前预警通过对配电网进行灾害下故障率建模以实现对后续决策的支持；灾前规划是通过对储能等一些灵活性资源进行合理配置来提升系统自身抵御灾害的能力；灾后调度主要通过对物资或者维修人员的规模和路线制定应急调度策略以保证最快时间恢复停电负荷。本文从灾前的角度对配电网韧性提升进行规划。

目前，在灾前预警和规划过程中存在以下问题：

1）灾前预警环节中，台风灾害下配电网故障率模型中一般将断线故障和倒塔故障看做是2 个互不影响的独立事件进行处理，但实际上断线和倒塔具有相关性，一个杆塔的倒塌会影响与之通过线路相连的相邻杆塔，使该相邻杆塔的故障概率增加，进而使另一个与之相连的杆塔故障概率增加，即故障具有传递性。因此，有必要在配电网故障率建模中考虑相关性影响；

2）故障率模型中一般仅考虑台风这一因素，实际上复杂的地理因素也会对模型产生影响，故考虑地理因素是有必要的；

3）灾前规划过程中，常规的韧性量化指标不能表示单个负荷变化对指标的影响，也不能体现灵活性资源供电支撑对系统韧性的影响，需要对指标进行改进来适应本文模型。

针对上述问题，本文的整体规划思路如下：

1）建立计及相关性影响的台风灾害下配电网故障率模型，充分考虑杆塔连接的故障传递相关性；引入信息扰动系数μ，根据已有的气象、地理的样本历史数据，通过RBF 神经网络构建气象、地理因素与μ之间的输入-输出非线性映射关系，通过上述模型来近似代替难以求解的高精度原模型，即形成代理模型来表征其对配电网故障率的影响。由于μ 的取值与气象、地理的样本历史数据有关，故也可用于反映配电网故障的不确定性。

2）建立台风灾害下灵活性资源韧性规划模型，并提出一种新的韧性量化指标，既可以表达单个负荷变化对电网韧性的影响，又体现了灵活性资源的供电支撑对电网韧性的影响。模型上层以韧性量化指标最优为目标函数，下层以规划建设运维成本、失负荷成本最低为目标函数，通过求解器对模型进行求解。

根据上述思路得到本文整体框架如图1 所示。图中：Ti，D为灾害期间节点i 负荷的停电时间，节点i是否发生故障取决于故障率模型得到的配电网故障信息情况；Ti，FR为灵活性资源供给电能的时间。

2 计及相关性的台风灾害下配电网故障率模型

2.1 基于模型驱动的配电网故障率建模

2.1.1 台风风速模型

台风风速模型由气象模型和实际观测数据建立，采用Holland 模型［12-13］来描述。台风范围内各点与风速的函数关系为：

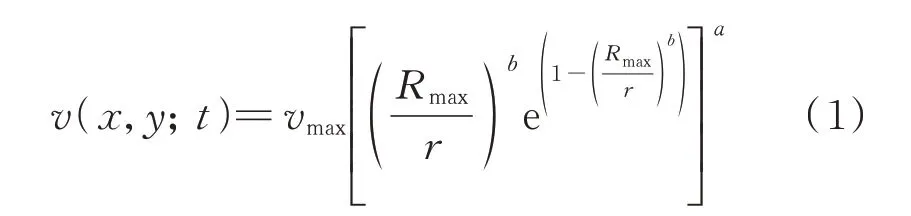
式中：vmax为最大风速；Rmax为最大风速半径；r 为线路位置(x，y)到台风中心的距离；a 为风廓线形状比例参数；b 为Holland 经验参数。

2.1.2 杆塔线路故障相关性建模

为考虑杆塔之间相关性对故障概率的影响，本文采用PageRank 算法［14］进行相关性建模。PageRank 算法是互联网中的一种网页检索排序方法，用Pr值来表征此网页被访问的概率，其值越高排名越靠前。因此，可以将相连杆塔之间的故障相关性看做页面之间的连接关系，当某一线路的第1个杆塔发生故障后，整个线路即视为故障，由于相关性的影响会导致该线路所有杆塔的故障率相较于传统模型整体升高，符合实际情况。

该算法的核心思想为：若一个杆塔连接着许多其他杆塔，说明这个杆塔较“重要”，该杆塔的Pr值会相对较高；若一个Pr值很高的杆塔A 连接着另一个杆塔B，则被连接的杆塔B 的Pr值也会相应提高。

第j 个杆塔的Pr值为：

式中：n 为区域内杆塔总数；μ 为信息扰动系数，μ=ργ，其中ρ 为气象扰动系数，γ 为地理扰动系数；α 为页面由一个网络节点传递到下一网络节点的概率，通常取0.85；Mj为与杆塔j（j=1，2，…，n）相连的杆塔；C(Mj)为第j 个杆塔的出链数目。

各个杆塔的Pr值可由一个n 维向量Pr来表示：

式中：nj和nl分别为与节点i 相连的杆塔数和线路数。

2.2 基于数据驱动的信息扰动系数计算

在数据驱动部分使用RBF 神经网络预测模型进行建模。RBF 神经网络由Broomhead 和Lowe 提出，因其建模过程简单、自适应性强、预测速度快，适用于对非线性模型的建模［15-16］。

杆塔的Pr值同时受气象、地理因素的影响，若一个杆塔相较于其他杆塔处于不利的气象或地理条件中，其倒塌的概率必然会增大，则该杆塔的影响力权重也会增加，使Pr值增加。因此，上文引入信息扰动系数μ 来表征气象、地理因素对杆塔Pr值的影响。

采用超拉丁立方抽样［17］对气象、地理信息样本数据进行采样，获得初始训练样本集为：

3 台风灾害下灵活性资源韧性规划模型

台风灾害发生时，分布式电源中的风电和光伏电站在极端天气下一般无法作为灵活性资源对电网提供供电支撑［18］。因此，对分布式电源的可控性有较高的要求，燃气轮机（gas turbine，GT）作为出力可控的分布式发电机可满足上述要求。本文选取的灵活性资源为：GT、电网侧电池储能电站（energy storage system，ESS）和电动汽车充电站（electric vehicle charging station，EVCS）。

本文采用双层规划模型：上层模型以韧性量化指标为最优决策灵活性资源的位置和容量、灵活性资源供电时间，并将上层规划结果以机会约束的形式传递到下层模型中；下层模型以总成本最低为目标，修正灵活性资源的位置和容量。

3.1 上层模型

EVCS 不同于ESS 与GT，在对EVCS 进行规划时，应优先考虑满足用户的充电需求［19］，其次才是作为灵活性资源对电网提供供电支撑，本文站在电网运营商的角度对EVCS 进行规划。假设规划区域内电动汽车总量为k，则EVCS 总容量NE为：

式中：fm，EV(t)为第m 个电动汽车充电容量变化曲线［20］；Emax为EVCS 所能配置的最大容量。

3.1.1 上层目标函数

上层目标函数为韧性量化指标R1。目前，在韧性指标的建立过程中常以配电网功能损失部分与时间轴的积分作为韧性量化指标［21-22］，如附录A 图A1和式（12）所示。

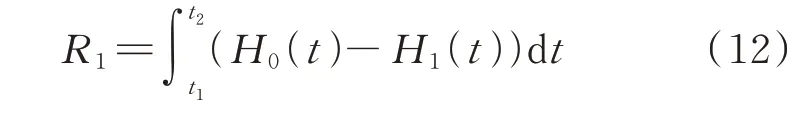
式中：t1和t2分别为灾害开始造成损失的起始时刻和系统刚好完全恢复到正常状态的时刻；H0(t)为正常场景下的系统性能运行函数；H1(t)为灾害场景下的系统性能运行函数。

指标R1虽然可以表示电网的整体韧性，但并不能表示单个负荷对韧性指标的影响，且该指标无法体现灵活性资源供电支撑对电网韧性的影响。因此，指标R1不适用于本文所述模型。

本文将整个灾害过程中所有负荷的正常运行时间与灾害持续影响时间的比值作为韧性量化指标R，即

式中：Ti，GT、Ti，ESS和Ti，EVCS分别为节点i 的GT、ESS和EVCS 供给电能的时间。

韧性指标R 既可以表达单个负荷对电网韧性的影响，又体现了灵活性资源对韧性指标的影响，适用于本文模型。

3.1.2 上层约束条件

上层约束包括配电网潮流约束和灵活性资源约束。

1）配电网潮流约束

功率平衡约束：

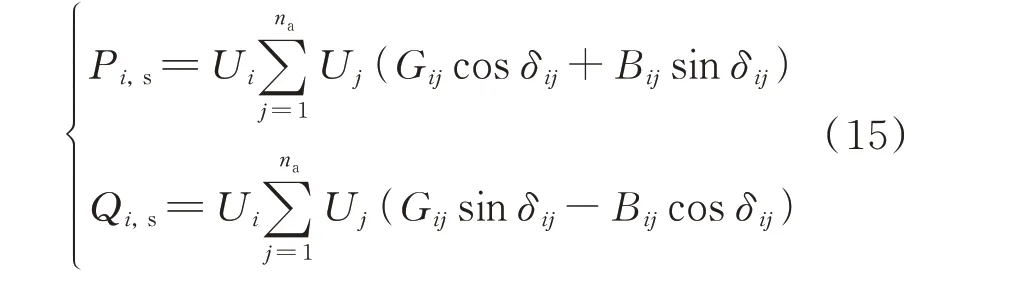
式中：Pi，s和Qi，s分别为节点i 的有功和无功注入功率；Ui和Uj分别为节点i 和j 的电压幅值；Gij、Bij和δij分别为节点i 与节点j 之间的电导、电纳和相角差。

电压偏差约束：

式中：E 为区域内充电桩所能提供的最大容量；ξEV为电动汽车充电负荷与充电桩所能提供的最大容量之比，取1.1。

3.2 下层模型

将电动汽车看做是一种储能设施，主要通过车辆入网（vehicle to grid，V2G）模式实现与电网间的双向电能流动。V2G 可以为电网提供调峰、调频及旋转备用服务［23］，本文主要考虑将电动汽车作为旋转备用资源为电网提供供电支撑。

3.2.1 下层目标函数

本文站在电网运营商的角度进行规划，将电网运营商作为ESS、GT 和EVCS 的投资主体，所需的总成本CCOM由配置运行ESS 和GT 成本、电动汽车的V2G 成本和失负荷成本构成，其表达式如下：

式中：KEV为投资等效系数；cEV为单位投资价格；ni，EV为节点i 的电动汽车充电桩的数量；v 为含电动汽车充电桩的节点集合；ρEV和uEV分别为EVCS 的造价和维护费用；cre和Pre分别为V2G 备用补偿费用和备用容量；cop和PV2G分别为V2G 备用容量费用和V2G 可用功率。

失负荷成本CLOSS为：

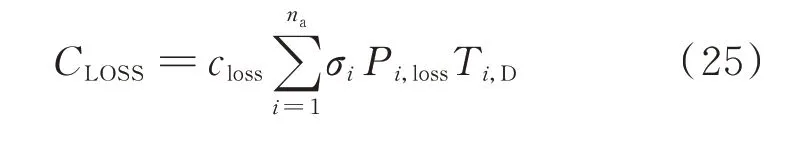
式中：closs为失负荷成本系数，与故障随机性相关，表达式见附录A；σi为节点负荷重要性权重；Pi，loss为节点i 失去的有功负荷。

3.2.2 下层约束条件

除上层规划的约束条件外，将上层规划结果以机会约束的形式添加到下层模型中。机会约束的表达式如下：

式中：Pr(·)为概率函数；EFR，Total为灵活性资源提供的供电电能；αr为置信水平。

3.3 模型求解

先将机会约束转化为线性约束，具体方法见附录B，线性化后利用MATLAB 工具箱中的YALMIP 调用商业求解器GUROBI 8.1.1 进行快速求解，并获得较为理想的结果。

4 算例分析

4.1 参数设定

本文采用改进的IEEE 33 节点配电网测试系统对上述模型进行仿真，该系统网架结构如附录C 图C1 所示。其中，电压基准值为12.66 kV，功率基准值为10 MW，系统负荷为（3 715+j2 340）kV·A。配电网架空线型号为LJ120，阻值参数为0.27 Ω/km。附录C 表C1 中给出了该配电网各个支路的电阻和长度，可知其空间范围规模约为40 km。

假设该配电网位于某近海岸处，台风相关参数设置如下：台风由坐标（45，0）向（0，30）方向移动，示意图见附录C 图C2；登陆时刻为08：00；移动速度为20 km/h；台风内部最大风速vmax=60 km/h；陆地最大风速半径Rmax=50 km；风廓线形状比例参数a=0.5；Holland 经验参数b=1.75。

根据配电网空间规模、台风移动速度和台风半径可知，由台风外径进入开始到台风外径完全离开结束，整个配电网受到台风影响的持续时间为7.7 h。为保留一定裕度，仿真模拟时间设为8 h，每20 min 检测一次配电网故障情况。

ESS 的单位功率成本系数为1 100 元/（kW·h）；贴现率为10%；运维成本系数为30 元/（（kW·h）·a）；总容量为2 MW；额定功率为150 kW。GT 的单位功率成本系数为200 元/（MW·h）；额定功率为150 kW；天然气单价取2.3 元/m3；机组发电效率为30%；天然气低热热值取9.5（kW·h）/m3。每个EVCS 含10 个充电桩，每台充电桩的V2G 功率为15 kW。失负荷成本系数为80 元/（kW·h）。

4.2 规划结果

文中收集了近3 年来登陆福建省的400 组台风历史样本数据，每组数据中包含台风期间最大风速、坡中朝向、坡中角度、坡中位置、下垫面、粗糙度、海拔高度7 种信息，原始数据来源于电力公司，有较高的可信度。

首先，对数据进行预处理，具体方法见附录D；然后，将采集的气象、地理样本数据进行批量学习训练，得到的学习训练结果如附录D 图D1 所示。随着训练次数的增加，训练集的学习精度指标减小，当训练到第88 次时出现最小误差，之后训练误差增加的原因是出现了过拟合现象，过拟合连续增加20 次后训练停止，即第88 次训练为最优结果，此时误差为6.082 7×10-8，接近于0，训练效果较好，对应的信息扰动系数μ 为1.744。

由于杆塔的数量较多且距离较近，采用平均值合并法对每个节点附近的杆塔进行合并，然后使用Z 分数进行检验筛选［24］。

根据第1 章的方法计算各节点处的Pr值，绘制各节点Pr值曲线，如图2 所示。

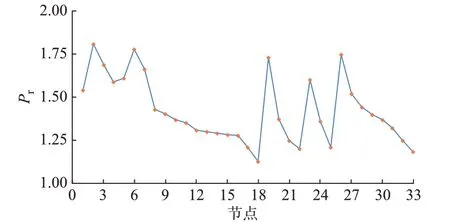
图2 各节点Pr 值曲线Fig.2 Pr value curve of each node

由图2 可知，连接架空线越多的节点的Pr值越大，而其临近节点的Pr值也会因该节点的相关性影响而增大。Pr值越大的节点，其发生故障失负荷的概率越高。

台风灾害结束后的配电网故障信息及分布情况如表1 和附录D 图D2 所示。

表1 故障发生时刻及受损线路Table 1 Fault moments and damaged lines

由上述数据可知，故障率较高的节点线路在台风灾害开始后的较早时段受到破坏，且故障规模较大。随着时间的推移，个别故障率较低的线路（9-10、14-15）也会发生故障，但其故障规模相对较小。

通过第2 章的模型对灵活性资源进行计及相关性影响的台风灾害下选址定容规划，规划结果如附录D 表D1、图D3 所示。由规划结果可知，通过灵活性资源的合理配置可节省失负荷成本39.09 万元，韧性指标也由0.593 2 提升至0.835 6。

通过规划还得到EVCS 在应急供电时的充放电曲线，如附录D 图D4 所示。由于EVCS 用于V2G的功率较低，可用容量较小，在对电网提供供电支撑的时间较短，相较于其他灵活性资源，将EVCS 的V2G 作为旋转备用对于灾害应急支撑的作用有限。因此，V2G 更适用于电力用户的分时电价管理，参与电能现货市场和调频市场，提供调峰、调频等辅助服务。

4.3 对比分析

4.3.1 配电网故障率模型

为验证本文配电网故障率模型的有效性，设置了如下3 种场景进行仿真对比分析：

1）场景1：即本文模型，计及相关性影响，使用数据-模型双驱动的方法建立配电网故障率模型进行灵活性资源规划。

2）场景2：未考虑相关性影响，去掉场景1 中的Pr值参数，使用数据-模型双驱动的方法建立配电网故障率模型进行灵活性资源规划。

3）场景3：计及相关性影响，将数据驱动部分的μ 值置为1，即仅使用台风机理对配电网故障率模型进行建模，然后进行灵活性资源规划。

上述场景得到的台风灾害下各节点故障率变化曲线如图3 所示。场景2 中未考虑相关性影响的台风灾害下配电网故障分布如附录D 图D5 所示。

图3 台风灾害下配电网各节点故障率变化曲线Fig.3 Failure-rate variation curves of each node in distribution network under typhoon disasters

由图3 和附录D 图D5 可知，与场景1 相比，由于场景2 未计及相关性影响，其故障率分布较为随机，导致预测的实际损坏线路分布随机性强，不符合配电网的实际受损情况。由附录D 图D2 与图D5 对比可知，较长线路配置的杆塔多，连接相关性强，使得该线路的故障率比邻近短线路的故障率高。文献［25］给出了台风灾害下某地区实际配电网故障率统计情况，满足上述相关性分布规律，与场景1 分布相同，同样证实了本文模型的有效性。场景1 与场景3 相比，故障率分布较为一致，但由于场景3 未采用数据驱动的方法，仅计及了相关性台风机理模型，未考虑气象、地理因素对配电网故障率的影响，导致各节点故障率值低了3.3%。

对上述3 种场景进行灵活性资源规划时，场景2由于损坏线路分布随机性强，EVCS 单位建设成本比ESS 和GT 低，模型中为综合成本考虑，会在分散的故障节点多配置5 个EVCS，而因为EVCS 作为旋转备用对配电网故障节点供电支撑能力有限，导致切负荷成本相较场景1 多出21.39 万元，所优化的韧性指标并不理想。场景3 中配电网整体故障率值低3%，所配置的灵活性资源容量较场景1 少13.71%，规划结果较为保守，由于场景1 考虑了气象、地理因素，需要多增加灵活性资源来应对实际更为严重的失负荷损失，从而保障配电网的韧性。

综上，计及相关性影响使配电网故障率分布更为合理，而考虑气象、地理因素使配电网故障率整体增加3.3%，约占总故障率的14%，不能忽略。因此，场景1 相比于场景2 和场景3 对配电网故障率的建模更为准确与合理。

4.3.2 优化模型

为验证本文灵活性资源选址定容双层规划模型的合理性，设置了如下3 种场景进行对比分析：

场景4：即本文模型，采用双层规划模型，上层模型以韧性指标最优为目标，将规划结果添加至下层模型的约束中，下层模型以经济性最优为目标，将规划结果反馈到上层模型中。

场景5：以韧性指标最大和经济性最优为目标建立灵活性资源多目标选址定容模型，通过模糊指派法对目标函数进行转化，采用非支配排序遗传算法-Ⅱ（non-dominated sorted genetic algorithm-Ⅱ，NSGA-Ⅱ）进行求解。

场景6：不计及经济性优化，仅考虑韧性指标最优化的灵活性资源单目标选址定容模型。

上述3 种场景目标函数的优化结果如附录D 表D2 所示。

根据优化结果可知，与场景4 相比，场景5 使用了较少的灵活性资源容量，但失负荷成本升高，最终总成本略低于场景4。尽管场景4 总成本略高，但该场景模型中优先考虑了配电网的韧性提升，对主次矛盾进行了划分，在成本提升的可接受范围内保证了配电网韧性，同时验证了本文模型的有效性。而场景6 未计及经济性优化，灵活性资源容量配置充足，使得当故障发生时灵活性资源可以提供足够的应急供应，直到转供电源介入时停止，从而保证负荷不会失电。但场景6 的规划方法所需成本较高，故在预算有限的情况下，本文的灵活性资源选址定容双层规划模型更为适用。

5 结语

本文计及了杆塔故障的相关性，基于数据-模型双驱动构建了计及相关性的台风灾害下配电网故障率模型；以韧性量化指标最优和经济性最大化为上下层目标函数，构建计及相关性影响的台风灾害下灵活性资源选址定容双层规划模型，并通过实际算例验证了模型的有效性。主要结论如下：

1）计及相关性的配电网故障率模型改善了传统故障率模型受损线路杆塔随机分布的缺点，更全面地反映了配电网的实际受损情况；

2）数据-模型双驱动的建模方法较好地解决了配电网故障率建模过程中样本数据较少和气象、地理因素模型复杂的问题；

3）灵活性资源可以在故障发生时为故障节点提供应急供电支撑，通过对灵活性资源进行合理的选址定容规划，可以在有限成本情况下有效改善配电网韧性，降低失负荷量；

4）EVCS 用于V2G 的功率较低，可用容量较小，对电网提供供电支撑的时间较短，相较于其他灵活性资源，将EVCS 的V2G 作为旋转备用用于灾害应急支撑的作用有限。

本文研究过程中，仅从灾前规划的角度对灵活性资源进行了选址定容规划，后续将会在本文的基础上对灾后资源进行动态调度以最大限度地保证配电网的韧性。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。