中国地方政府债务与国债间风险传导机制研究——基于新冠肺炎疫情冲击前后的联合动态建模

■ 朱广印，张胜全，刁伟涛，褚福崴

一、引言

新冠肺炎疫情作为突发公共事件对我国金融市场运行产生了重大影响。受共同风险敞口机制影响，金融体系较疫情前整体波动性明显加剧，系统性风险显著上升（方意等，2020）。市场不确定性和政策环境等多方面因素共同触发资产配置调整机制，大量资金由高风险市场转移至低风险市场。由于疫情初期大量避险资金涌入债市，导致利率债需求大幅上升，同时经济预期的不确定性也降低了市场的风险偏好，不同期限国债收益率均出现震荡下滑，地方债利差走势也趋于分化，短期信用利差下行，长期信用利差上行，共同推动地方债利差期限结构走阔。

2015 年新《预算法》实施，地方政府被赋予举债融资的法定权利。随着发债规模不断扩大，地方政府偿债压力逐步显现。截至2020 年底，我国地方政府债务余额总量达25.66 万亿元，较2014 年底增加了66.04%。存量债务日益积累，与经济下行压力加大，流动性风险显著攀升相互叠加，地方政府债务风险在不断积聚。如何治理地方债务风险这个“灰犀牛”问题，如何识别并防范地方债务风险可能引发的系统性风险，成为了亟待解决的重大问题。

本文基于我国地方政府债券的风险溢价以及对于国债定价和风险的影响这一角度，研究地方政府债务的系统性风险及其传导渠道。通过构建国债收益率与代表性地方债券风险因子的联合动态模型，试图探究如下相互联系但各有侧重的问题：（1）在中央财政和地方财政内在联系所导致的隐性担保和救助预期下，地方债务风险如何通过影响国债收益率因子和收益率曲线的动态变化，从而产生潜在的系统性风险？（2）作为反映宏观经济运行情况重要指标的国债收益率如何影响地方债务风险？（3）新冠肺炎疫情作为负面外生冲击，是否会影响这种传导机制？

二、文献综述

一是国债利率期限结构与宏观经济指标的相关研究。早期有关利率期限结构理论的研究主要侧重于如何提高收益率曲线的拟合效果。Nelson & Siegel（1987）最早提出 Nelson-Siegel（NS）模型，将债券收益率用四个具有经济含义的时间序列数据进行解释，拟合出不同形态的收益率曲线。目前为止拟合国债收益率曲线较为成熟的模型主要是动态NS 模型和无套利NS模型。孔继红和岳伟（2020）在对国债即期收益率进行研究时发现相较于无套利NS 模型，动态NS 模型在实证上表现更好，代价是存在无套利的理论缺陷。Ang&Piazzesi（2003）首次将宏观经济指标与国债收益率曲线进行联合建模，通过构建宏观金融模型探究国债收益率曲线与各种经济因素间的动态联系。帅昭文等（2017）将CPI 和工业增加值增长率引入无套利宏观金融模型中研究其与国债收益率曲线的关系，结果表明CPI 增长率通过影响短期国债收益率以影响国债收益率曲线，而工业增加值增长率则通过影响长期收益率影响收益率曲线。货币政策对不同期限国债收益率的影响效果不同，并且对短期利率的影响强于对长期利率的影响（关禹等，2019；唐博和张凌枫，2021）。

二是地方债务风险与系统性风险相关研究。牛霖琳等（2016）首次将城投债信用利差作为反映地方债务风险的指标引入宏观金融模型中，建立无套利NS 模型研究我国国债收益率与城投债利差因子的动态联系，发现城投债风险可能引发系统性风险，提高国债的风险溢价。Chen&Wang（2015）发现，如果政府的隐性担保被认为是可信的，那么其与发债主体的自身显性信用和投资预期收益都会影响中国城投债的利率高低。Ang et al.（2015）发现中国整体的债务风险和货币政策因素对城投债定价具有显著影响。毛锐等（2018）通过构建地方债务与金融风险间的迭代模型研究发现，中央对地方隐性担保率不断下降的同时，金融部门的系统性风险和持有地方债的风险将会对应上升。朱莹和王健（2018）在研究城投债风险溢价时引入市场约束，发现“自发自还”方式所产生的市场约束能显著降低城投债的风险溢价。目前相关研究大多以城投债为研究对象或衡量指标，用城投债信用利差来反映或代表地方债务风险。但是随着2015年新《预算法》赋予地方政府自主举债融资的权利，融资平台被逐步剥离政府融资职能，城投债的地方债务特征或地方政府信用背书逐步淡化，地方政府债券成为地方政府唯一的合法举债方式。

三是新冠肺炎疫情对金融市场冲击相关研究。蓝波和庄雷（2021）发现新冠肺炎疫情的传染性对货币市场的冲击具有阶段性影响，而对债券市场具有阶段反转性影响。方意等（2020）利用事件分析法量化新冠肺炎疫情对我国金融市场的冲击，发现不同市场风险溢出效应显著上升且存在较大差异，虽然冲击初期市场间替代效应和风向共振效应均有增强，但相对于其他市场，对债券市场的影响并非持续上升，而是间接上升的。

基于现有文献发现地方债券的研究基本是空白的，有关新冠肺炎疫情对我国金融市场影响的研究也往往侧重于整体。鉴于此，本文尝试从两方面对地方债务风险研究进行补充：一是借鉴国债宏观金融建模思路，将地方债券信用利差作为衡量地方债务风险的宏观经济指标融入DNS-VAR模型中，对国债和地方债进行整体性研究；二是对比新冠疫情外生冲击前后，国债收益率与地方债务风险间的联系与动态变化，并基于国债与地方债间的关联识别研究地方债务的系统性风险。

三、DNS-VAR模型的构建

为了避免内生性问题所导致的参数估计结果不一致性，本文使用动态的NS 模型。首先对国债收益率进行分解，将分解得到的具有不同经济含义的三个因子与地方债利差因子构建向量自回归模型，最后通过脉冲响应函数和方差分解识别因子间的相互作用效果。

动态的 NS 模型（Dynamic Nelson-Siegel，DNS）表达式为：

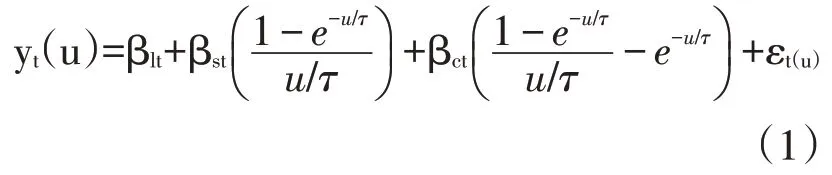
其中，y（u）表示t 时刻剩余期限为u 的国债即期收益率，β、β、β分别表示t 时刻剩余期限为u的国债收益率的水平因子、斜率因子和曲率因子，分别具有长期、短期和中期的含义。具体表现为当剩余期限u趋向于无穷大时，即期收益率y（u）趋向于水平因子β，此时y（∞）可以表示长期国债收益率；斜率因子β表示长短期利率之差，通常为负，表明收益率曲线具有单调上升的趋势；曲率因子β表示收益率曲线的弯曲程度。τ为衰减因子，用以刻画斜率因子荷载和曲率因子荷载随剩余期限u的衰减速度。

t时刻不同到期期限DNS模型测量方程为：

本文在已有研究的基础上对溃坝生命损失估算公式中的风险人口死亡率作了如下调整：式中，f0为我国风险人口死亡率取值参考文献；α为灾害严重性程度系数；m1为生命损失直接影响因素的灾难程度影响因子，m1＜1；m2为生命损失间接影响因素的灾难程度影响因子，m2＜1；k 为权重系数，0.5＜k＜1；β 为修正系数，β=1.4。

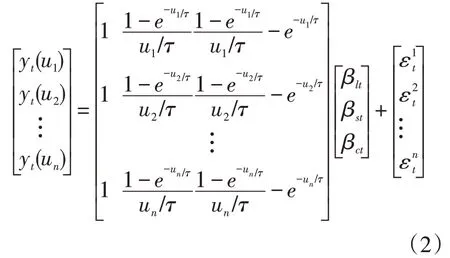
地方债务风险采用同时期、同期限地方债与国债的利差因子进行测度：

Sp表示t时刻剩余期限为u的地方债利差，Lb表示t时刻剩余期限为u的地方债收益率。

最后选取DNS模型中分解出的水平、斜率、曲率因子和地方债利差因子构建VAR（4，p）模型：

四、数据说明

（一）数据描述

本文选取银行间债券市场固定利率国债和地方债2015年1月至2020年12月每周最后一个交易日数据作为研究对象，设置13 个不同的固定期限，分别为1、2、3、6、9、12、36、60、84、108、120、180、360 个月，共3744 个观测值，数据来自Wind数据库。相关描述性统计见表1和表2。

表1 中国国债收益率描述性统计

2015—2019年2020年期限平均值之差1 2 3 6 9 1 2 36 60 84 108 120 180 360样本数261 261 261 261 261 261 261 261 261 261 261 261 261平均值2.415 2.466 2.516 2.637 2.697 2.743 3.029 3.183 3.360 3.361 3.363 3.736 4.057标准差0.480 0.471 0.469 0.482 0.473 0.474 0.390 0.373 0.339 0.336 0.336 0.338 0.321样本数52 52 52 52 52 52 52 52 52 52 52 52 52平均值1.627 1.735 1.844 2.081 2.141 2.187 2.524 2.724 2.981 2.985 2.989 3.510 3.834标准差0.367 0.407 0.455 0.553 0.518 0.507 0.477 0.378 0.276 0.247 0.239 0.243 0.211-0.788-0.730-0.672-0.556-0.556-0.556-0.505-0.459-0.378-0.376-0.373-0.225-0.222

表2 中国地方债收益率描述性统计

2015—2019年2020年期限平均值之差1 2 3 6 9 1 2 36 60 84 108 120 180 360样本数261 261 261 261 261 261 261 261 261 261 261 45 23平均值2.728 2.778 2.828 2.950 3.013 3.065 3.343 3.524 3.705 3.725 3.743 3.993 4.151标准差0.534 0.528 0.529 0.547 0.544 0.546 0.461 0.439 0.404 0.406 0.404 0.111 2.076样本数52 52 52 52 52 52 52 52 52 52 52 52 52平均值1.746 1.844 1.941 2.158 2.225 2.304 2.699 2.992 3.207 3.286 3.386 3.746 4.044标准差0.378 0.411 0.448 0.524 0.504 0.492 0.438 0.343 0.236 0.242 0.267 0.232 0.168-0.982-0.935-0.888-0.792-0.788-0.761-0.644-0.532-0.498-0.439-0.358-0.247-0.108

2020 年各期限国债平均收益率较2015—2019 年均有所下降，主要原因是受新冠肺炎疫情负面冲击，我国金融市场不确定性显著上升，中央银行为防范化解系统性风险，采用逆周期的货币政策，下调利率。市场不确定性加之投资者避险情绪，大量资金流入风险相对较低的债券市场，共同触发资产配置机制，从而导致作为安全资产的国债价格被抬升、收益率下降。另外，在疫情负面影响背景下，不同期限国债收益率对市场利率下降的敏感性也不同，其中，短期国债收益率波动尤为明显，下降幅度约在55bp-78bp，而决定长期国债收益率的因素更为复杂，因此长期国债收益率下降幅度较小，约为22bp-37bp。长短期国债收益率对疫情负面冲击的不同反应也共同推动了收益率曲线整体趋于陡峭。

由表2 可知地方债收益率与剩余期限呈同方向变化，体现为流动性溢价，另外其标准差与剩余期限呈反方向变化，表明长期地方债收益率较短期地方债收益率更为稳定。由图1看出，2020 年前各期限地方债利差分布较为集中，而自新冠肺炎疫情暴发后，各期限地方债利差走势开始分化，特别是疫情初期，资金出于避险目的，导致短期信用利差下行，长期信用利差上行，共同推动地方债利差期限结构走阔。

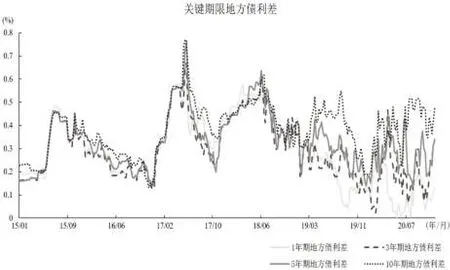
图1 关键期限地方债利差

（二）数据处理

本文使用卡尔曼滤波法拟合全参数DNS 模型估算得到的衰减因子17.98（1/τ=0.056），利用MATLAB对国债收益率曲线进行拟合，分解得到β因子，结果列于表3。

表3 DNS模型参数估计值

变量2015—2019 βl βs βc βl 2020 βs βc样本数261 261 261 52 52 52平均值3.940-1.431-1.179 3.700-1.895-1.300标准差0.296 0.421 0.753 0.139 0.353 0.987最小值3.184-2.861-3.273 3.341-2.772-3.689最大值4.605-0.336 0.918 3.883-1.433 0.269偏度-0.235-0.311 0.329-1.115-1.239-0.793峰度2.546 3.687 2.863 3.357 3.635 3.282

图2 国债收益率曲线三因子

2015年至今，地方债发行期限以1、3、5、7和10 年期为主，且5 年期占比最高，因此文章选取5 年期地方债利差作为地方债务风险的代表性因子。在5%的置信水平条件下对国债收益率因子和地方债利差因子的时间序列进行平稳性检验，对未通过ADF单位根检验的因子，进行一阶差分，结果列于表4。根据AIC 准则可以确定模型的滞后阶数为3阶，同时矩阵的特征根均落在单位圆内，模型通过稳定性检验。

表4 β因子与利差因子ADF单位根检验

年份P P 2015—2019参数D（βl）D（βs）参数βl βs βc Z（t）-15.617-14.845 0.0000 0.0000平稳性平稳平稳Sp βl 2020 βs βc D（Sp）D（βl）D（βs）D（βc）-14.972-7.322-5.292-7.975 0.0000 0.0000 0.0000 0.0000平稳平稳平稳平稳Sp Z（t）-2.089-2.764-4.381-2.523-1.954-1.401-1.764-3.241 0.2492 0.0637 0.0003 0.1099 0.307 0.5816 0.3983 0.001平稳性非平稳非平稳平稳非平稳非平稳非平稳非平稳平稳

五、联合动态分析

对通过平稳性检验的β因子和代表地方债务风险的5 年期地方债利差构建VAR（3，4）模型，根据脉冲响应图和方差分解结果识别冲击响应。

（一）脉冲响应分析

基于Cholesky 法分解得到的脉冲响应图可以识别随时间变化，国债收益率因子与地方债务风险因子间相互冲击的程度大小和持续时间长短。图3—4 中的实线表示脉冲大小均值，虚线表示置信水平为90%，横轴表示向后20 期（周）的冲击响应时间，因子间一单位正向冲击大小为冲击变量的一个标准差。

图3表示疫情冲击前，国债三因子和地方债利差因子间的脉冲响应图，其中一单位地方债利差因子对国债三因子的冲击大小约为12个基点，一单位水平、斜率和曲率因子对地方债利差因子的冲击大小约为29、42和75个基点。

图3-a 显示地方债利差因子的正向冲击会导致水平因子同方向变动、斜率因子反方向变动，在国债收益率曲线上反映为曲线长端上移，并且斜率增大。地方债利差因子的正向冲击通常是由于地方债务风险增大所导致的，具体表现为地方政府信用下降。因此当地方债务风险增大时，资产配置机制发挥作用，投资者选择持有信用水平更高且流动性更好的短期国债替代地方债，导致地方债利差上升的同时也压低了短期国债收益率，而资金的避险需求和长期再融资成本共同提高了长期国债收益率中的风险溢价。因此，地方债务风险加大，在导致短期国债收益率下降的同时，提升了长期国债收益率，从而推动国债收益率曲线斜率增大。

图3-b 显示地方债利差因子对水平因子和斜率因子的冲击更为敏感，即使曲率因子对其冲击达到峰值时，也仅为0.02-0.03 个单位（约为1.5-2.25bp）。这表明地方债利差的变动主要是由长短期国债收益率变动引起的，中期国债收益率的变动对地方债风险波动的解释程度并不显著。其中，水平因子对利差因子在中短期内表现为显著的正向冲击，短期内迅速上行，随后逐渐衰减，而斜率因子和曲率因子对利差因子的冲击短期内表现为正向，中长期逐渐转负。

图3 2015—2019年因子间的冲击响应

图4 为疫情冲击后国债三因子和地方债利差因子间的脉冲响应图，其中一个单位的地方债利差因子对国债三因子的冲击大小约为7 个基点，一个单位的国债收益率水平、斜率和曲率因子对地方债利差因子的冲击大小约为14、35和98个基点。

对比图3 和图4，国债收益率因子和地方债利差因子间的冲击方向在疫情前后基本一致，但冲击幅度有所增大、冲击时间也有所延长。这表明新冠肺炎疫情的冲击作用不但没有改变地方债与国债间的风险传导机制，反而增强了这种机制。原因可能是国债收益率作为其他固定收益证券和利率衍生品的定价基础，疫情期间地方债利差对其动态变化也更为敏感。但是值得注意的是，疫情带来的负面影响和宽松型货币政策等一系列利好信号的交互对冲决定了债券市场所受的影响并非持续上升，而是间歇性上升的，具体表现为地方债利差因子与国债收益率间的冲击呈波浪式上下震荡，因子间冲击存在多变性和滞后性。

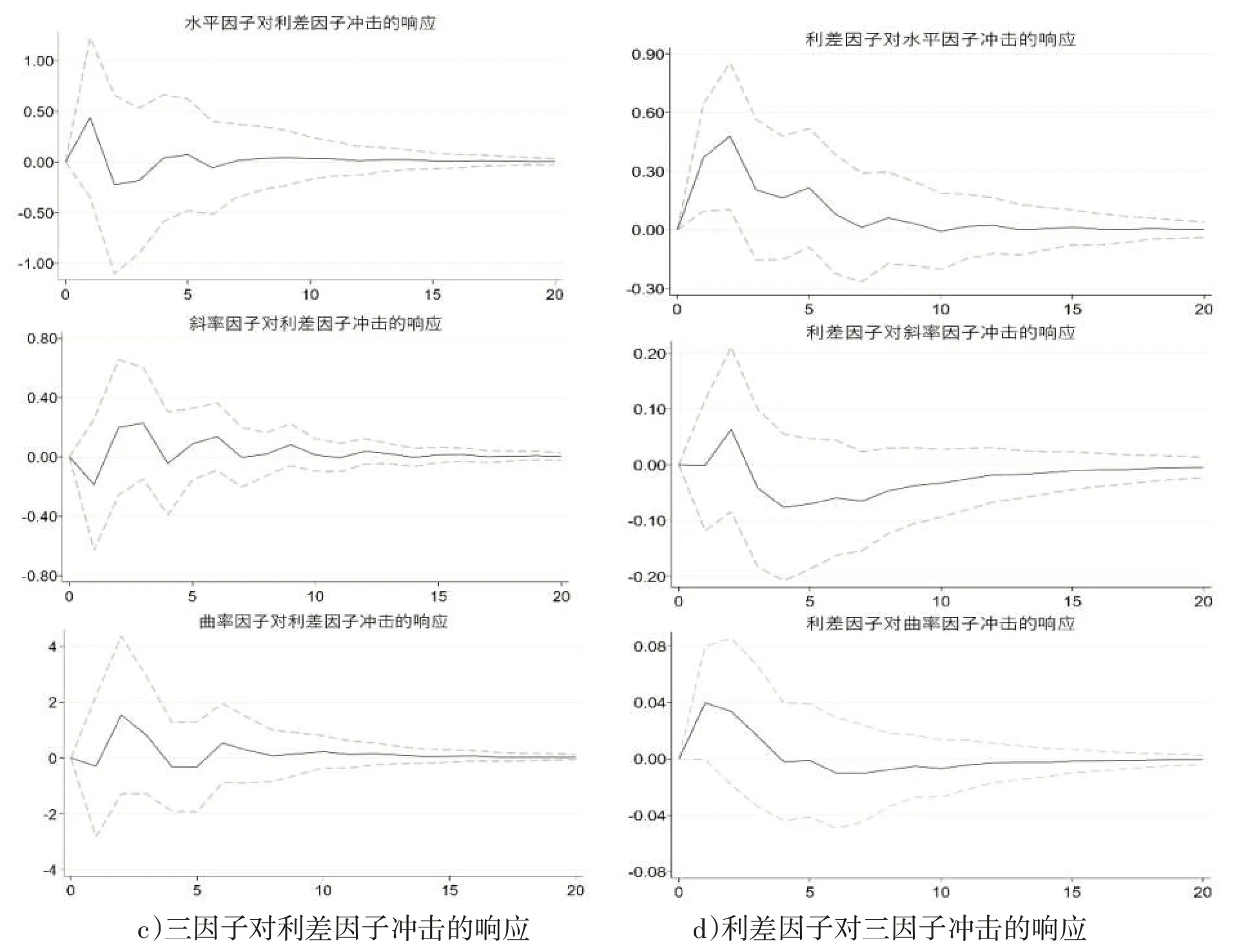
图4 2020年因子间的冲击响应

（二）方差分解分析

由表5 的国债收益率因子与地方债务风险因子方差分解结果可知，各因子方差波动主要受其自身冲击的影响。疫情期间除曲率因子外，其他因子对自身波动的解释程度均有所下降，而利差因子对收益率因子波动的解释程度有所上升，表明疫情期间收益率因子与地方债利差因子间冲击效应大于疫情前。

表5 因子间方差分解

注：此处的收益率因子β和地方债利差因子S均为表3中通过平稳性检验的序列。

因子向后预测2015—2019 2020 βs βc Sp βl βs βc Sp βl 3 9 1 βs 5 3 9 1 βc 5 3 9 1 Sp βl 5 3 9 1 5 98.91 97.77 97.65 0.92 1.50 1.56 27.82 27.72 27.71 3.37 3.38 3.38 0.42 1.14 1.22 98.48 97.33 97.21 30.03 28.93 28.85 6.41 6.42 6.42 0.56 0.98 1.03 0.57 1.11 1.20 42.13 43.33 43.41 0.32 0.34 0.33 0.88 0.87 0.87 0.12 0.12 0.12 0.04 0.00 0.06 89.88 89.85 89.85 80.67 79.17 79.00 5.26 8.19 8.20 26.78 27.08 27.03 21.96 21.96 21.95 10.91 10.44 10.41 65.93 62.36 62.32 18.49 18.39 18.40 1.18 4.32 4.72 6.26 6.41 6.41 26.88 27.33 27.33 52.79 52.04 51.99 2.83 4.21 4.66 2.16 3.98 4.18 1.93 2.12 2.15 1.94 2.49 2.58 74.03 69.51 68.67

六、结论和启示

本文将反映地方债务风险的5 年期地方债利差作为宏观变量引入利率期限结构模型中，通过对地方债务风险与国债收益率进行联合建模探究新冠肺炎疫情前后两者间的动态联系与风险传导机制。结果显示：地方债务风险通过两个渠道影响国债收益率，一方面地方债务风险增大使得短期国债收益率降低，说明资金出于避险目的，投资于风险更低的国债，从而推高国债价格并降低短期收益率；另一方面地方债务风险上升推动国债长期收益率上升，意味着地方债务风险传导至中央层面，即使存在中央政府救助兜底的市场预期，但形成的系统性风险仍然会推升中长期收益率的上升。另外，在新冠肺炎疫情冲击下，地方债务风险与国债收益率间的交互作用效果呈现“多变性”和“滞后性”的特点，这主要是由于市场系统性风险骤升与宽松型货币政策等一系列利好信号交互对冲的结果。

上述结论主要有如下两方面的启示：第一，虽然省级地方政府拥有了自主发债的权利，但是市场对于地方债券的定价仍然受隐性担保或救助预期的影响，地方债务风险传导到中央政府从而引发系统性财政金融风险的可能性仍然存在。因此，要以打破地方政府的预算软约束和救助预期为核心抓手和关键举措，来进一步提升地方债券定价的市场化水平，隔离地方与中央的债务风险。第二，地方债务问题既与财政体制有关，也与金融体系有关，因此地方债务风险的防范化解要充分加强财政政策与货币政策的协调配合。