过程控制系统中的双容水箱液位恒值控制研究

石博轩 王俊伟 娄凌浩

摘 要：过程控制实验系统在高校和科研中应用比较广泛，双容水箱液位控制系统具有单输入、单输出、非线性、时变和滞后性的特征，本文以天煌教仪THJDS3型过程控制实验平台中的双容水箱液位作为被控制对象，通过该系统建立双容水箱液位的传递函数数学模型，设计了PID控制器，并用MATLAB对上述控制系统进行了仿真研究，对实验结果进行了分析。

关键词：过程控制;双容水箱液位控制;数学模型;非线性;PID控制器

Research on Constant Liquid Level Control Algorithm

of Double Tank in Process Control System

Shi Boxuan Wang Junwei* Lou Linghao

Hetao University，College of Mechanical and Electrical Engineering Inner MongoliaBayannur 015000

Abstract：The process control experimental system is widely used in Colleges and universities and scientific research.The double tank liquid level control system has the characteristics of single input，single output，nonlinearity，timevarying and hysteresis.This paper takes the double tank liquid level in the thjds3 process control experimental platform of Tianhuang teaching instrument as the controlled object，and establishes the transfer function mathematical model of the double tank liquid level through the system，The PID controller is designed，the above control system is simulated with MATLAB，and the experimental results are analyzed.

Keywords：Process control;Liquid level control of double tank;Mathematical model;Nonlinearity;PID controller

1 概述

双容水箱液位控制系统在化工、电力和高等学校教学和科研中应用比较广泛，尤其是液位的恒值控制。通過在高校过程控制实验平台上模拟液位的控制为工业中的实际应用和培养学生工程实践能力奠定基础。

双容水箱液位恒值控制具有单输入、单输出、非线性、时变性和滞后性等特点[1]，被控对象双容水箱由上下两个水箱组成，被控对象双容水箱的控制输入为液体流量，输出量为液位，控制的难点是实现液位精确和快速控制。针对以上控制要求，孙明格等[2]开发了LabVIEW的双容水箱液位控制系统，具有一定的应用价值。孙悦等[3]通过比较方法，设计了PID控制、模糊控制和模糊PID控制的液位控制，通过比较得到模糊PID控制的最佳控制性能。李磊等[4]设计了量子群优化算法的PID双容水箱液位控制系统，控制性能优于传统PID控制器。李大字等[5]设计了双容水箱液位自抗扰控制系统（ADRC），并与传统PID控制进行了对比实验，ADRC调节时间短和调节速度快，但超调量较大。李辉等[6]将具有相轨迹云模型的控制器应用到三容水箱液位控制系统中，具有一定的创新性。Meng X等[7]针对四容水箱非线性和耦合性，提出了一种非线性扰动观测器（NDOB）来估计扰动并用于补偿控制，并与纯PID控制进行了对比实验，结果表明NDOB具有更好的控制性能。

本文是详细介绍了被控对象双容水箱的数学模型中的传递函数建立过程，并设计了传统的PID控制器实现了液位的恒值跟踪控制。

2 过程控制实验装置介绍

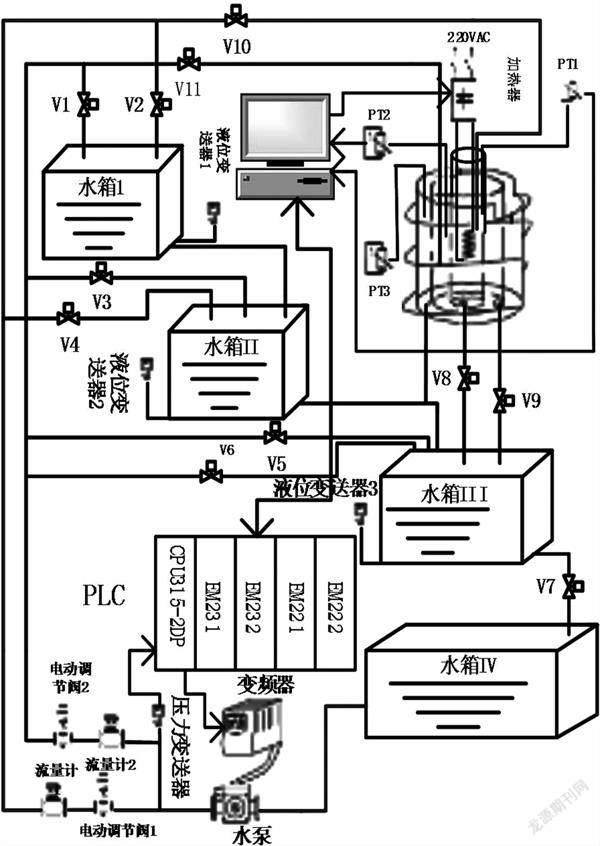
过程控制实验装置采用天煌教仪THJDS3型过程控制实验平台。实验装置如下图1所示。加热筒分为三层：内筒最高，通过V10手动调节阀门可以向内筒注水;中间筒低于内筒，通过V11可以向中间筒注水;外层筒环抱中间筒，其作用是当中间筒注水溢出的时候，可以将水再收集并回流到下面的大水箱中;压力变送器将水的压力（0～0.1MPa）转换为4～20mA的电流信号送给PLC;PLC作为PID运算控制器可以输出4～20mA电流信号，作为变频器输入信号，变频器的频率输出对应0～50Hz，不同的频率对应不同的水泵转速，从而实现电机变频调速和改变抽水的速度。压力变送器、水泵和PLC控制器构成闭环控制使水管内的压力值稳定在某一设定值，以实现变频恒压供水。

电动调节阀的输入信号是4～20mA，输出开度是0～100%，输入的电流信号不同，则调节阀的开度也不同，从而可以调节注水速度、压力和流量;内筒装有电阻加热器，加热器电压0～220V对应控制电流4～20mA。改变输入控制电流，可以调节加热器的加热电压，从而改变加热的速度。内筒加热可以同时升高内筒和中间筒的温度，同样改变中间筒注水的速度，也能同时降低内筒和中间筒的温度。本文控制的目的就是控制内筒的加热速度和中间筒的注水速度，使内筒和中间筒的温度分别稳定在不同的温度。设计水箱Ⅰ、水箱Ⅱ、水箱Ⅲ的目的是可以做双容水箱液位控制实验。

3 双容水箱模型

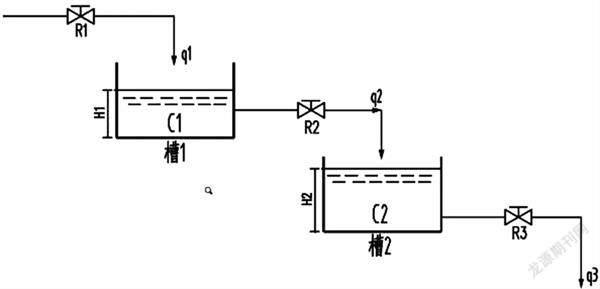
双容水箱结构图如图2所示，包括气动调节阀、电磁流量计、磁翻板液位计、压力变送器、上下水箱、电磁阀和抽水泵等。

其中R1、R2、R3表示管道液阻，q1、q2、q3表示流量，H1和H2表示液位高度。

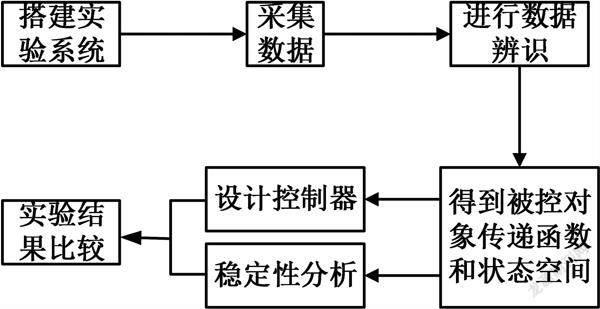
下面对双容水箱模型的传递函数进行建模，实验建模的流程图，如图3所示。实验重点是被控制对象数学模型建立、控制器的设计和控制算法的选择。

根据图2的双容水箱模型，根据物料平衡方程，可得如下微分方程：

q1-q2=AdH1dt（1）

q2-q3=AdH2dt（2）

其中A为两个双容水箱的底面积，对（1）和（2）式求拉氏变换得：

Q1（S）-Q2（S）=ASH1（S）（3）

Q2（S）-Q3（S）=ASH1（S）（4）

根据阀门液阻与液位高度关系，可得如下关系式：

Q2（S）=H1（S）R2（5）

Q3（S）=H2（S）R3（6）

分别联立（3）和（5）式，（4）和（6）式得到如下传递函数：

Q2（S）Q1（S）=1AR2S+1（7）

Q3（S）Q2（S）=1AR3S+1（8）

下面以Q1（S）為输入量，H2（S）为输出量，结合（6）、（7）、（8）式得到双容水箱的所对应的数学模型传递函数如下：

G（S）=H2（S）Q1（S）

=Q2（S）Q1（S）H2（S）Q3（S）Q3（S）Q2（S）

=1AR2S+11AR3S+1R3

=R3（AR2S+1）（AR3S+1）

考虑到双容水箱的滞后性，令T1=AR2，T2=AR3，K=R3，得到最终传递函数：

G（S）=K（T1S+1）（T2S+1）e-τS（9）

在图1的基础上，打开阀门V4和V7，使水箱Ⅱ和水箱Ⅲ构成双容水箱系统，Ⅳ水箱作为储水箱。其中V4全开，V7达到适当开度。在手动状态下，打开水泵，使气动调节阀1开度分别在10%、30%和60%三种情况下，每隔10s记录一次水箱Ⅲ液位数据和水箱Ⅱ输入流量数据，直到液位分别达到相应的平衡为止停止记录数据，共测量100组数据。

利用测量的100组数据，将数据导入MATLAB 2018b/System Identification工具箱中，对采集到的水箱液位高度数据进行模型辨识，最终得到的传递函数模型为：

H2（S）Q1（S）=5.8（122.1S+1）（132.2S+1）e-48.5s（10）

4 控制系统设计和仿真

根据建立的双容水箱数学模型，设计了如图4所示的控制系统，其中双容水箱液位模型如式（10）所示。

上述控制器中的PID三个参数分别设置为kp=150，ki=0.132，kd=2400，采用的PID算法是增量式PID算法，增量式PID算法如式（11）所示，其中u（k）为控制律，e（k）为液位偏差，液位设定值为100mm。

Δuk=u（k）-u（k-1）

=kpe（k）-e（k-1）+kie（k）+

kde（k）-2e（k-1）+e（k-2）（11）

控制系统的MATLAB仿真图，如图5所示。

结语

通过建立双容水箱的数学模型，并应用PID控制进行了液位的恒值控制，控制性能较好，为后续智能控制算法的改进奠定基础。

参考文献：

[1]周依涛，郑炜炀，项思哲，高金凤.基于滑模控制的双容水箱液位系统设计[J].国外电子测量技术，2021，40（06）：5458.

[2]孙明革，张嘉诚.基于LabVIEW的双容水箱液位控制系统研究[J].科学技术创新，2021（17）：184185.

[3]孙悦，恒庆海.基于DCS的双容水箱液位控制系统仿真[J].计算机仿真，2020，37（12）：219223.

[4]李磊，李俊红，顾菊平，华亮.双容水箱基于QPSO算法的PID控制研究[J].控制工程，2021，28（08）：15531558.

[5]李大字，李国强，张建青.双容水箱液位自抗扰控制系统稳定性分析及实验教学设计[J].实验技术与管理，2021，38（07）：6366+72.

[6]李晖，邢振登.一种基于相轨迹特征的云模型控制器设计[J].控制工程，2020（9）：14891494.

[7]Meng X，Yu H，Zhang J，et al.DisDisturbance observerbased feedback linearization control for a quadrupletank liquid level system[J].ISA Transactions，2021.

项目：内蒙古自治区国家级大学生创新创业训练计划项目（项目编号：202011631004）

*通讯作者：王俊伟（1985— ），男，内蒙古包头人，硕士，讲师，主要从事非线性控制、最优控制等方面的教学与科研工作。