针对锋电位的启发式阈值检测算法

王 洁，郭天翔，卢云山，赵 冰，熊 鹏，杜海曼

1.河北大学 电子信息工程学院，河北 保定 071000

2.康泰医学系统（秦皇岛）股份有限公司，河北 秦皇岛 066004

现代多模态颅内记录设备逐渐具备植入式脑机接口系统高时空分辨率的要求[1]，测量细胞活动的最流行技术之一是使用细胞外电极阵列。现有多电极技术已经能够同时记录数千个神经元锋电位（spike）的电活动[2-3]。与细胞内活动记录不同，这些细胞外记录不是直接接触神经元的，而是需要处理电极记录的信号来提取电极周围不同细胞发出的锋电位信号，锋电位信号的检测性能是随后信号特征检测及聚类等智能分析的基础和前提，在大脑探索及脑类疾病的预防检测中意义重大，应用范围从神经编码、脑类认知到军事医学等[1，4]。

锋电位检测的准确性影响着后续脑电信号特征提取和聚类精确度[5]。目前已有多名研究人员和团队在此领域做出贡献。上个世纪由Turin[6]最早提出的检测到锋电位的方法为匹配滤波，它能从单电极采集的信号中识别出神经元，匹配滤波的思想是将观察到的信号匹配到神经元锋电位模板，在误差范围内匹配的信号将被认为是锋电位。然而，该方法不适应现代多电极采集的锋电位信号检测，且检测精度较低。为了减少计算复杂性、节约时间并适应多电极针信号采集，文献[7]使用了振幅阈值法，即只有当振幅越过预定义的阈值时检测到的信号为锋电位信号，但是根据数据标准差公式或人工手动选择的阈值虽在高信比噪数据中有较高检测准确性，但其对于低信噪比数据检测精度仍有待提高。随着小波在锋电位检测中的使用，低信噪比下的锋电位检测精确度明显提升，但其在计算上要求很高，此外，小波检测算法的精度在很大程度上取决于其对母小波的选择。近年来，具有瞬时特性和较低计算资源需求优势的非线性能量检测算法（non-linear energy，NEO）在电信号的检测中也得到了广泛应用[8-9]，但当NEO应用于低信噪比植入式脑电数据时，检测精度不能满足信号分析的需求。文献[10]在NEO基础上提出了一种混合的神经元峰值检测算法——缩放性能量检测算法（scaled energy operators，SEO），虽降低了功耗，但其锋电位检测精度有待进一步提高。文献[11]提出了一种基于稀疏表示和形态成分分析的锋电位检测算法，加强了该算法的抗噪能力以及适应能力，但耗时长，需要提高求解速度。在文献[12]中，为提高锋电位信号的检测能力，提出了基于CUDA的实时锋电位分析系统框架[12]，但是其文献中假设的神经元信号和噪声都是高斯分布，对检测含不确定背景噪声的信号可能会有较高的错误率。文献[13]针多通道微电极阵列记录的锋电位的微弱性以及易受干扰特性，结合主成分分析（PCA）小波分析，提出PCA-小波（PCAW）与整体平均经验模态分解（EEMD）联合的去噪新方法（PCWE），但是该方法在低信噪比信号中表现较差，需加强该算法的鲁棒性。由此可见，根据以上文献所总结，锋电位检测的难点在于所提检测算法既要适应现代多电极针数据采集，锋电位波形随电极针位置或细胞内电流的类型以及空间分布造成的低幅值特点，也要在因背景环境干扰造成含不确定背景噪声数据中保持较高的检测精度。

综上所述，为了解决锋电位检测过程中因幅值较低和不确定背景噪声而出现的漏检、误检情况，本文提出了一种基于启发式阈值的锋电位检测算法。在该方法中首先对于一些低幅值锋电位信号，优化椭圆滤波器参数，降低有用信号衰减程度，保留原始信号中幅值较小的锋电位，然后使用启发式阈值检测公式，有效降低复杂采集环境中引入的混杂噪声干扰，实现脑电信号锋电位自动检测。

1 方法

本文在植入式脑电采集数据的锋电位的提取过程中，优化椭圆滤波器，保留了低幅值锋电位信号，同时结合针对不确定背景噪声的启发式阈值检测公式提出了一种新型锋电位检测算法，且对相关参数不断调整优化，将其应用在不确定背景噪声的猕猴肢体伸展抓握运动范式下获得的真实数据，以及具有低幅值锋电位信号的细胞外模拟记录数据中的5个不同信噪比数据中进行检测验证。

1.1 数据来源

实验数据部分主要由两部分组成：真实数据和模拟数据。真实数据来自于猕猴肢体伸展抓握运动范式，该范式中，猕猴需要伸手到指定目标位置处对目标物体进行抓握，在本次实验中，使用前2个通道的记录数据做相关分析。模拟数据来自英国莱斯特大学神经工程实验室提供的细胞外模拟记录数据[14-15]，该数据集源于真实的数据库及真实的模拟细胞外记录，团队根据噪声的振幅和频谱分布对背景噪声的模拟源于叠加大量不同振幅与频谱的锋电位信号，另外再在每个数据集中添加1个低信噪比、低幅值和高方差特性的多单元锋电位和2个频率较低但振幅相对较大的单单元锋电位。数据集中包含5个不同信噪比数据集，其信噪比按照给出的数据合成方式在该文献中分别标明为4，4，2，2，3[14]。

1.2 滤波

信号通常都有自身的幅频特性，且经由电极采集到的原始信号伴随噪声，考虑到锋电位信号本身特性，对于采集到的脑电信号要进行滤波操作。一般神经学定义突触间的电活动是低频慢波，称为局部场电位，通常在300 Hz以下。过高频率的波形都是噪声，一般在3 000 Hz以上。研究显示，数字滤波器的非线性相位响应可很大程度上扭曲锋电位形状[16]，且会改变信号伪影的外观，使其看起来与真实的脉冲类似，胞体的神经冲动都是比较高频的快波，故采用零相位滤波，使用300～3 000 Hz的带通椭圆滤波器对原始信号进行滤波，椭圆滤波器在通带和阻带内都是等波纹的逼近方式，相同阶数下相比于巴特沃斯、切比雪夫滤波器通带与阻带的逼近特性良好[17]。MATLAB的信号处理工具箱提供了设计椭圆滤波器的函数：ellip函数。

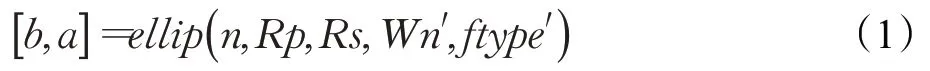
利用其可以设计高通（当ftype=high时）、或带阻滤波器（当ftype=stop，且Wn=[W1,W2]时）。参数n表示最小阶数，参数Rp表示通带最大波纹度（单位dB），参数Rs表示阻带最小衰减（单位dB），对于文中所评估的模拟数据，使用文献[18]所给的滤波器参数会导致一些在峰值较低且在阈值线的锋电位信号不能被检测，故将滤波器的Rp至1×10-6dB，有用信号尽可能无衰减的通过，保留原始信号中幅值较低信号的波形。

对来自莱斯特大学神经工程实验室的模拟细胞外记录数据集中的第3个数据集进行锋电位检测实验，此数据集所包含的2个单单元锋电位信号具备低幅值特点，如上图1所示，横坐标表示Rp值，纵坐标表示精确度，图1中的曲线则为各自对应的锋电位检测精度，从图中可以看出随着椭圆滤波器中的最大波纹度的数值的减小，锋电位检测精确度增大并逐渐趋于平稳，由于考虑到滤波器的引入会对原有信号带来损耗，所以选取相对较小的Rp值。

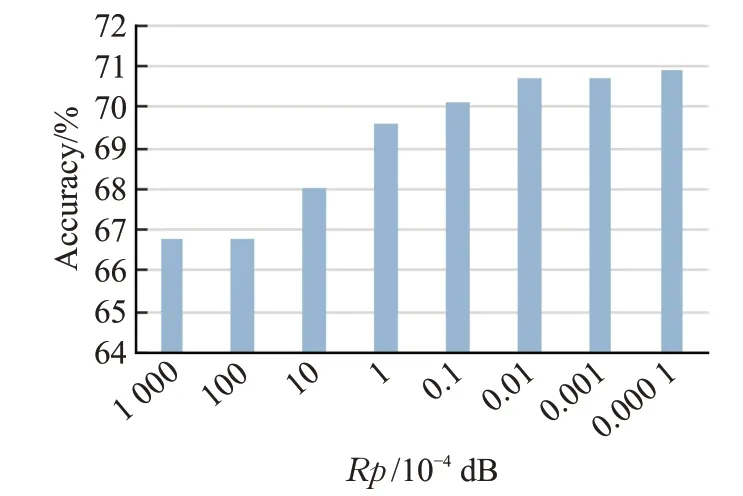
图1 不同Rp检测精度图Fig.1 Different Rp test accuracy diagram

1.3 阈值检测方法

本文使用四种阈值检测方法，分别对模拟数据和真实数据进行锋电位阈值检测并对比。在振幅阈值法中通常使用标准差阈值检测算法，表述为以下表达式，根据背景噪声对信号的影响，使用设置为4倍的噪声标准差为阈值来进行锋电位的检测[11]，表达式中的x是经过滤波器得到的滤波信号。

能量算法主要测量信号与其导数之间的交叉能量，这使得它们适合于峰值检测，因为锋电位峰值是神经信号的最高能量成分。Mukhopadhyay和Ray提出将非线性能量算法（NEO），如公式（3）所示用于锋电位信号的阈值检测。公式（4）中离散加速能量算法DEAO（discrete energy acceleration operator）在文献[10]中也被用于锋电位的检测，且在此文献中针对能量算法做了进一步改进，提出了公式（5）并将其用于低信噪比模拟数据，使其锋电位检测精度有了一定程度的提高。

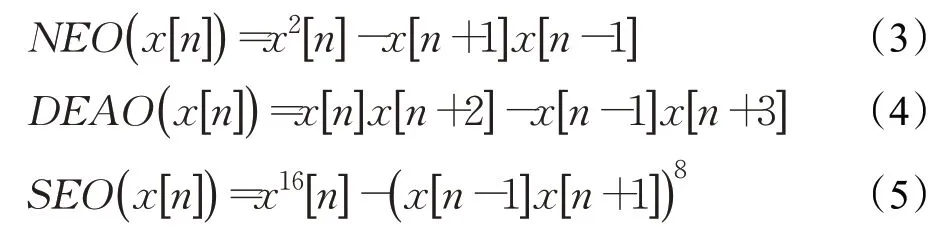
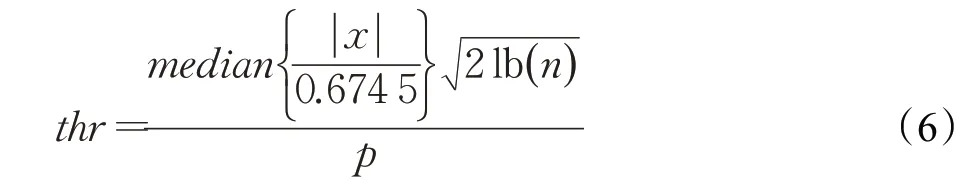
式中，增加了一个参数p，经过经验取值，当p=1.6时，锋电位检测的精确度最高。

2 结果与讨论

2.1 模拟数据

2.1.1 多种信噪比下锋电位检测精度

文中采用精确度（accuracy，ACC）作为衡量锋电位检测准确度的标准：

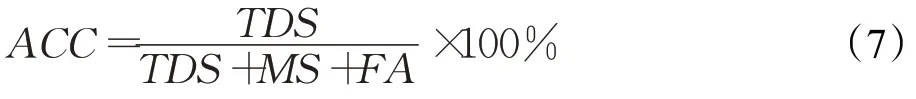
其中上述公式中正检数（truly detected spikes，TDS）为锋电位检测算法检出的正确的锋电位信号，漏检数（missed spikes，MS）为没有被检测出来的锋电位信号，误检数（false alarms，FA）为检测出来的不是锋电位信号的误检个数。

表1是莱斯特大学神经工程实验室提供的细胞外模拟记录数据的5个数据集的锋电位总数及多单元、单单元锋电位所占百分比，在所提供细胞外模拟记录数据集中，模拟数据3和4中拥有两个低幅值且形状相似的单单元锋电位信号。表2是3种不同的锋电位检测算法和本文所提检测算法分别在含不同信噪比、不同幅值大小锋电位信号的模拟数据集上的TDS、MS、FA及ACC对比。

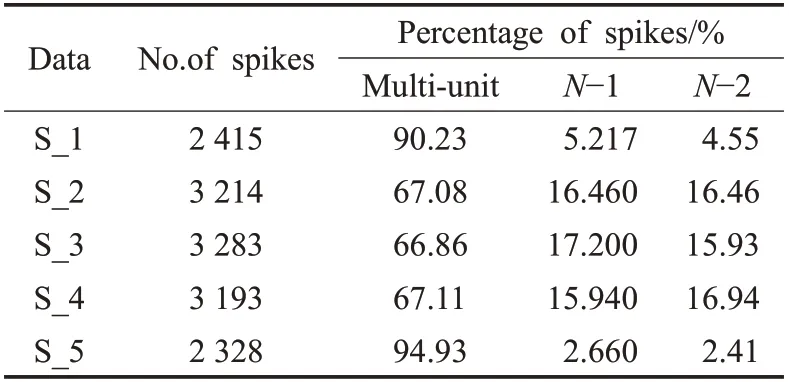
表1 模拟数据集中各种峰值单位的百分比Table 1 Percentages of various peak units in simulated dataset

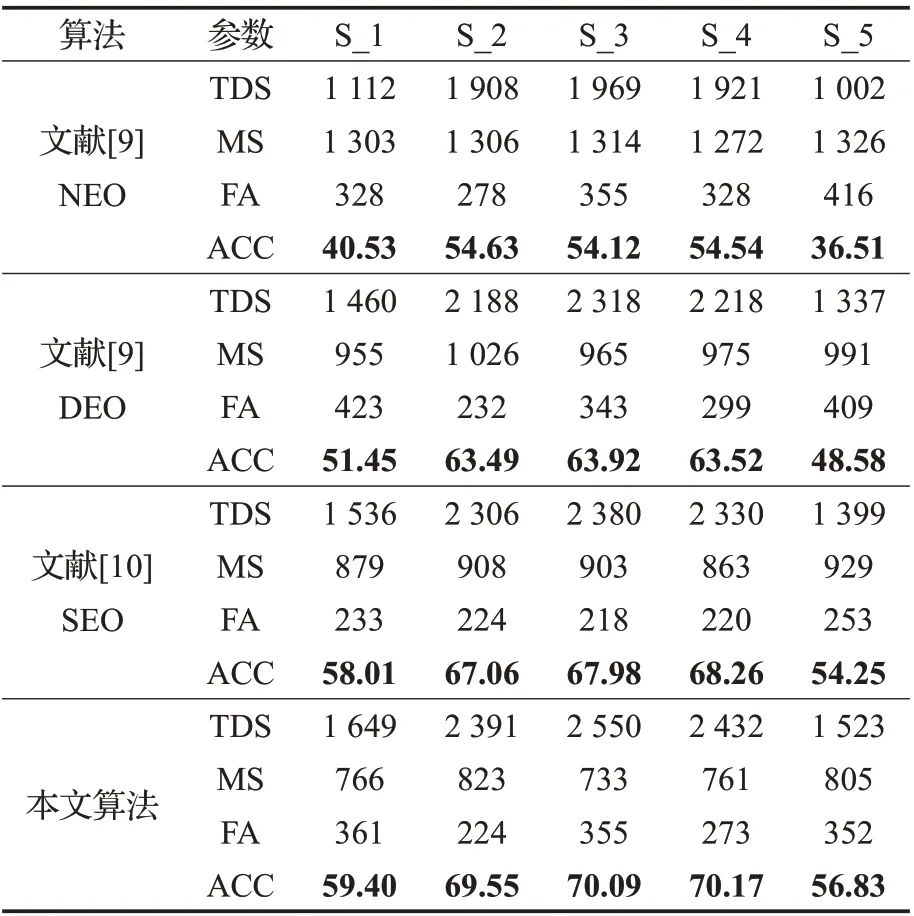
表2 不同锋电位检测算法检测精度Table 2 Detection accuracy of different spike detection algorithms

表1中的S_1到S_5是莱斯特大学提供的5个不同信噪比的细胞外模拟记录数据，其中，表格第2列代表各个数据集中的锋电位总个数，多单元与两个单单元锋电位所占百分比分别占据表的第3到5列，不难看出，每个数据集中两个单单元锋电位信号所占比例相似，而在数据集1与数据集5中多单元锋电位信号所占比例较大，在90%以上，且锋电位的总体数目相对较少。数据集2、3和4中锋电位总数在3 000以上，多单元锋电位信号所占比例为67%左右。

从表2可以看出，在锋电位检测精确度上，文献[10]中所提到的SEO检测算法要高于文献[9]中的NEO和DEAO，但是在本文所提算法中，锋电位检测精度相较于SEO算法在每个细胞外模拟数据集上都有一定的提高，这其中对于低信噪比的数据5来说，本文提出的锋电位检测算法对锋电位信号的检测精确度相对于给出的NEO、DEAO和SEO算法精度都要高，证明该方法可用于低信噪比信号检测。另外，在上表中还可观察到本算法在拥有两个较低幅值单单元锋电位信号的数据3中检测精确度也相对较高。为了更直观地表现出不同阈值检测算法的检测精确度，将其绘制成如图2所示。

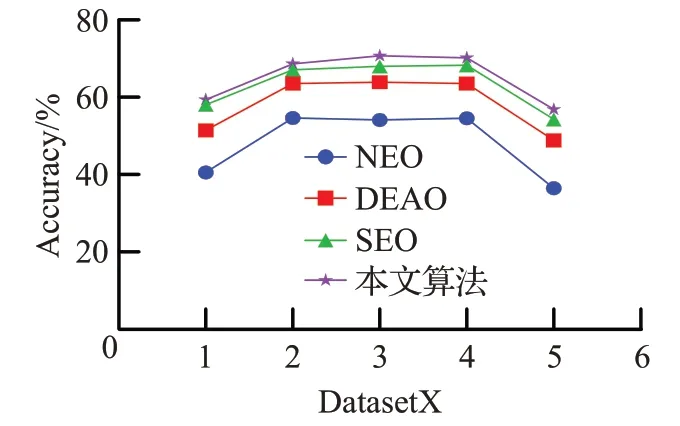
图2 4种阈值检测算法精确度图Fig.2 Accuracy of four threshold detection algorithms

图2中圆圈、方框和三角形分别表示5个模拟数据集分别经过NEO、DEAO和SEO检测算法的锋电位信号检测精度，五角星代表本文所提算法在不同信噪比下细胞外模拟数据集的锋电位信号检测精度。从图中的折线图中可以看出在不同信噪比下，数据中锋电位信号的检测精度是不一致的，且使用本文所提锋电位检测算法的精确度比其余能量算法都要高。

2.1.2 不同信噪比单单元锋电位检测精度

表3是这两个数据集分别经过两种不同锋电位检测算法计算并统计得出的漏检数和误检数。

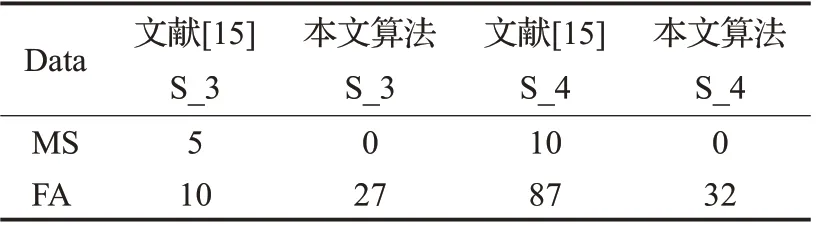
表3 数据3、4单元锋电位信号MS与FA数统计表Table 3 Data 3，4 single spike signal MS and FA statistical table

在表3中，第1列和第3列为经过文献[15]中的锋电位检测算法得出的漏检数和误检数，剩余两列为本文提出的检测算法得出的漏检数和误检数。在表3中可以看出，经过所提检测算法检测后的漏检数为0，且误检数较中值检测公式较低，因此本文方法对于模糊在阈值线附近的低幅值锋电位信号具有较优越的检测性能。

2.2 真实数据

在真实的猕猴肢体伸展抓握运动范式脑电信号采集过程中，会不可避免地受到噪声影响，造成信号背景噪声的不确定性，同时，真实的锋电位形态学特征也大有不同，幅值不尽相同，故而将提出的锋电位检测算法应用在上述范式所采集的真实数据中进行锋电位信号检测，并绘制出实验结果如图3所示。

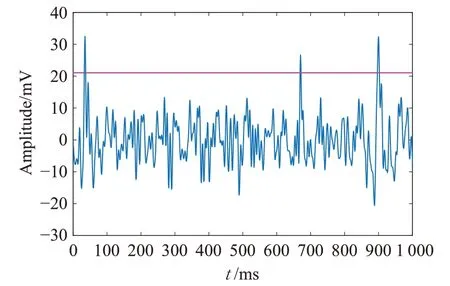
图3 真实数据锋电位阈值检测结果图Fig.3 Result diagram of realdata spike threshold detection

从图3中可以看见一条横亘于纵坐标的直线，这便是经过锋电位检测算法计算得出的阈值线，同时在图中也可观察到一些低幅值的在阈值线附近的锋电位信号被检测出。

为进一步验证由所提算法检测到的锋电位信号，对猕猴肢体伸展抓握运动范式下采集得到的真实植入式脑电数据分别使用主成分分析以及K多元均值方法进行了特征提取和聚类操作。这其中，数据具有不确定背景噪声，同时在进行锋电位信号检测前幅值大小未知。

在图4（a）和（b）中，分别使用了猕猴肢体伸展抓握运动范式下采集得到的脑电信号的前两个通道数据，经过本文锋电位检测算法检测后，再经上述特征提取并聚类后的锋电位信号结果图。从图中清晰地可以看出每个通道包含的不同的锋电位信号，说明本文锋电位检测算法可用于真实采集的含不确定背景噪声的植入式脑电数据，且从两个图中可以观察到，真实数据的幅值较低，从侧面验证了本文算法对低幅值锋电位信号的提取能力。

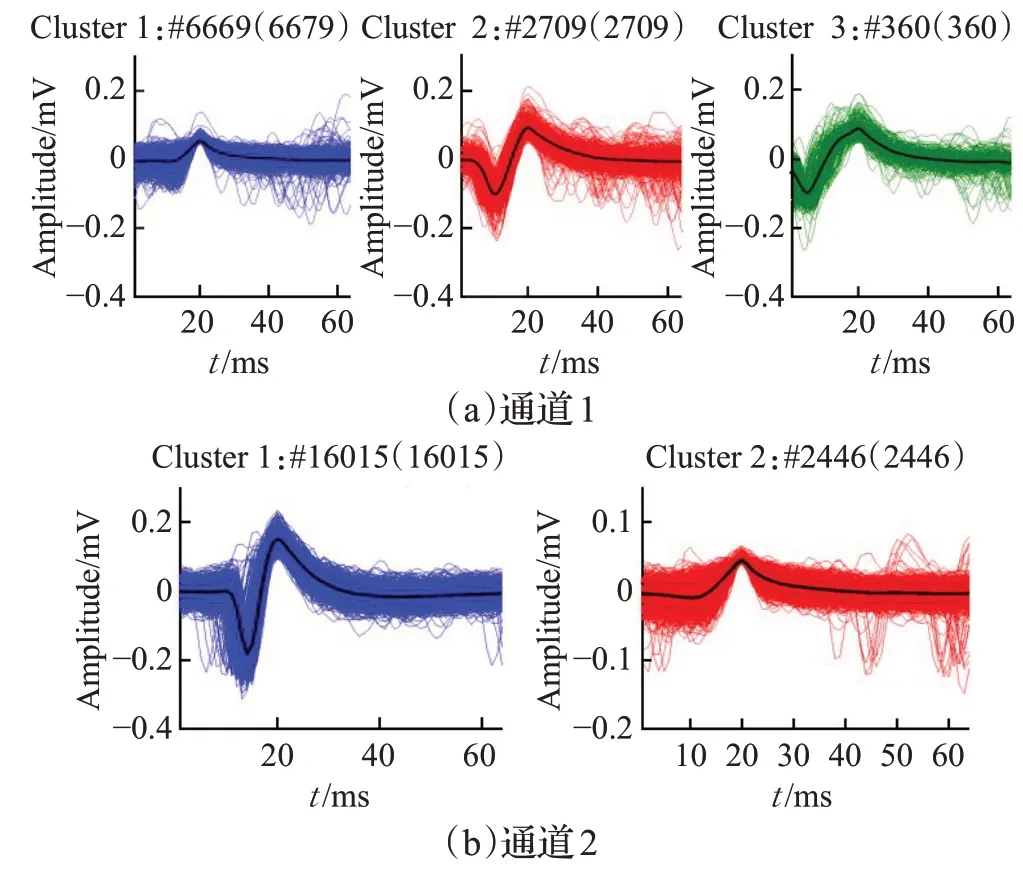
图4 真实数据锋电位分选结果图Fig.4 Result diagram of realdata spike sorting

3 结束语

本文主要针对含不确定背景噪声且低幅值的脑电数据采集信号提出一种基于启发式阈值的锋电位检测算法。将其用于低幅值且含不确定背景噪声的真实数据中进行验证，取得了良好的实验效果，同时也在多种信噪比的模拟细胞记录数据集下进行了相关锋电位检测实验并统计。实验结果表明，该锋电位检测算法对于低幅值的锋电位信号检测精度相对于一般或者改进的能量算法的检测精度要高一些，最优阈值下NEO的平均检测准确度为48.07%，DEAO为58.19%，SEO的检测准确率平均为63.11%，而本文所提算法达到了65.21%，在多种信噪比数据中检测精度相对突出。算法的开发也可同时减少专家手动标注阈值的复杂性，节省人力资源。但值得注意的是，即使新提出算法表现良好，但平均精确度仍待提升，所以要求研发者继续开发高效且精确度较高的锋电位检测算法。

致谢 本文实验中所使用的猕猴伸展抓握运动范式数据由军事医学研究院军事认知与脑科学研究所前沿交叉学科研究室提供，特别感谢该团队对本项工作的支持。