改进人工蜂群算法及其在边缘计算卸载的应用

章呈瑞，柯 鹏，尹 梅

1.武汉科技大学 计算机科学与技术学院，武汉 430065

2.智能信息处理与实时工业系统湖北省重点实验室，武汉 430065

随着5G通讯技术与物联网技术的发展，用户对AR、VR等计算密集型、时延敏感型应用的需求越来越高。根据思科2020年度互联网报告统计，预计到2023年全球移动设备将从2018年的88亿增长到2023年的131亿，连接到IP网络的设备数量将达到293亿高于2018年的184亿[1]。传统的云计算作为一种集中式计算，已难以在短时间内处理需要大量资源的应用程序。此外，由于云计算中心往往距离用户较远，也带来了数据传输时延高、能耗高等一系列问题。

为了应对这些问题，移动边缘计算（mobile edge computing，MEC）应用而生[2]，该模式通过云计算下沉，端计算上移来将移动智能终端及物联网设备的计算任务卸载至边缘云中，解决了传统云计算模式算力有限、时延较高的不足。

MEC计算卸载作为一个重要的研究方向，受到了国内外学者的广泛研究。目前对于计算卸载策略的研究主要包括三个方向，最小化时延、最小化能耗以及时延和能耗加权后最小化该代价函数[3]。

文献[4-7]侧重于对最小化时延的研究。文献[4]研究了多用户计算的划分以及云资源上卸载计算，设计了一个离线启发式算法，来解决计算卸载所面临的时延问题。文献[5]采用马尔可夫决策方法，根据任务缓冲区的排队状态、本地处理单元的执行状态以及传输单元的状态来动态卸载计算任务。文献[6]构建了一个带有能量收集设备的MEC系统，并提出了一种基于李雅普诺夫优化的动态计算卸载算法用以最小化时延。文献[7]提出了一种在MEC中使用排队网络和遗传算法的有效卸载策略，并与粒子群算法对比在最小化任务响应时延上取得了较好的效果。

文献[8-10]侧重于对最小化能耗的研究。文献[8]考虑了前向链路和反向链路的链路状况，运用离散的人工鱼群算法，在时延约束下，最小化能耗。文献[9]提出了一种车联网中的雾云计算卸载算法以最小化车辆和计算设施的能耗。文献[10]设计了一个考虑任务延迟的MEC系统，提出了一种联合优化资源分配和任务卸载分配的策略，用于最小化能耗。

文献[11-14]侧重于对时延和能耗进行联合优化。文献[11]通过为用户任务设置优先级，采用均衡传输性能的信道分配算法为卸载任务分配信道资源，实现计算资源最优配置，优化系统总增益。文献[12]研究了超密集边缘网络中的依赖关系任务卸载问题，提出一种启发式算法，在保证子任务之间依赖关系的同时，共同优化时延和能耗。文献[13]通过拉格朗日对偶分解将原问题分解成若干个子问题，在通信和计算资源约束下最小化执行时延和能耗的加权和。文献[14]考虑工业环境下的应用，采用离散的粒子群算法，使用惩罚函数来平衡时延与能耗。

通过分析以上研究，不难发现，文献[4-7]虽能够获得一个较好的时延，但并未充分考虑移动终端的能耗情况，这就会导致低电量设备仍可能会为满足最小时延要求，选择在本地计算，导致电量消耗更快。文献[8-10]能够对能耗进行较好的优化，延长终端设备的使用时间，但可能会导致某些对时延敏感的应用得不到及时的处理。文献[11]联合考虑了计算时延和能耗，侧重于对单一边缘服务器的优化，未能充分考虑系统整体的全局优化。文献[12-13]则难以解决多MEC多终端设备的卸载问题。文献[14]选用离散的粒子群算法求解时延与能耗的代价函数，取得了较好的效果，但由于粒子群算法的限制，在迭代后期仍然采用全维度更新策略，在高维问题上难以取得更好的收敛精度，且较容易陷入局部最优。

本文则在以上研究的基础上，考虑到真实环境中多移动设备多MEC服务器的情况，引入云服务器，从整体角度考虑，将能耗作为惩罚项构造代价函数，使用人工蜂群算法（artificial bee colony algorithm，ABC）[15]联合优化时延与能耗。

启发式算法在MEC卸载领域得到了很好的应用[7-8，14]，ABC作为经典启发式算法，被证明具有良好的全局收敛性[16]，具有收敛精度高，易于跳出局部最优等良好性质，近年来也在云计算卸载、雾计算卸载等领域获得较好表现。文献[17]提出一种混合队列蚁群和人工蜂群算法以解决移动云计算环境的任务分配及卸载，文献[18]针对智能电网的云雾计算场景，提出了一种混合人工蜂群优化算法（HABACO）进行仿真实验，获得较好的负载平衡效果。文献[19]在雾计算场景下利用ABC优化适应度函数来优化能耗、调度运行时间等，提升网络服务质量。以上研究均取得了较好的表现，但并不适用于MEC环境下高维、高并发的计算卸载。

由于蜂群的单维更新策略，导致算法前期在高维问题上收敛速度较慢，后期难以依靠个体本身的位置更新跳出局部最优，仅能依靠向侦察蜂转化来增强探索能力，对个体的开发能力有一定的损失[20]。故本文引入多维更新种群解决此问题，并通过种群间的转化平衡算法的探索和开发能力，使得算法能够在任意最大容忍时间限度内，获得较好的卸载方案。

1 系统模型

本文构建了一个云服务器辅助的多设备移动边缘计算卸载系统，移动终端设备或者物联网设备可以通过无线网络与MEC服务器或云服务器的基站进行通信。假定有M个移动设备。N个MEC服务器，1个云服务器，每一个移动终端产生任务后，可以在本地进行计算，也可以选择将任务卸载至边缘服务器或云服务器，即每一个任务会有N+2种可能的卸载结果，其卸载模型如图1所示。

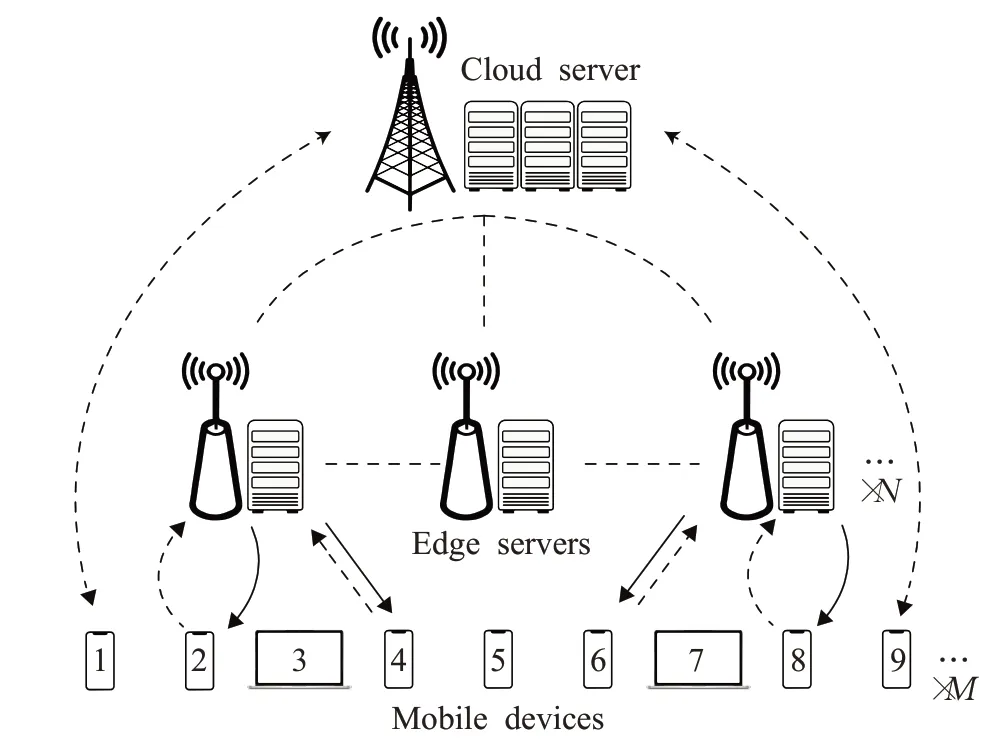
图1 卸载系统模型Fig.1 Offloading system model

1.1 本地计算模型

当移动设备或者物联网设备在本地计算时，其任务执行时间为：

其中Wi表示第i个设备产生任务的数据量，Flocal表示该设备本地计算的能力（每秒CPU周期数，单位为GHz），Tlocal表示在本地完成任务所需花费的时间。

本地计算的能耗为：

其中，Tlocal为本地计算的时间，Plocal为本地计算的功率，Elocal为本地计算的能耗。

1.2 卸载计算模型

每一个边缘移动设备产生的任务除了在本地计算外，还可以选择在边缘服务器或者云服务器进行计算。

当其卸载至边缘服务器时，其时延为：

卸载至边缘服务器的能耗为：

当其卸载至云服务器时，其时延为：

卸载至云服务器的能耗为：

假设，最终卸载结果为有a个任务在本地计算。则在本地计算的最大时延为：

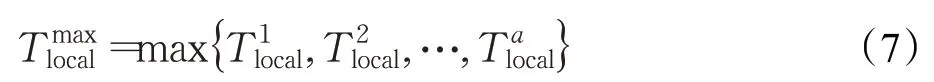
在边缘端服务器计算的最大时延为：

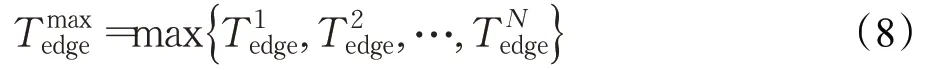
则该系统最终时延为：

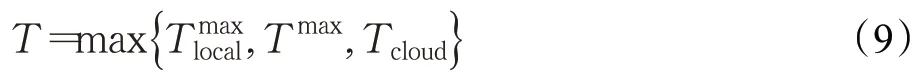
能耗为：

1.3 代价函数

将该问题转化为在能耗约束下最小化时延的问题，其总代价计算公式为：

其中g为惩罚系数，将当前系统总能耗作为一个惩罚项，以避免系统为最小化时延全部采用本地卸载，从而导致移动设备电量消耗增多。

2 基于ABC的优化

2.1 基本的人工蜂群算法

人工蜂群算法（ABC）是由Karaboga[15]于2005年根据蜜蜂的采蜜行为提出的一种群智能优化算法，ABC算法分为四个阶段：初始化阶段、雇佣蜂阶段、观察蜂阶段、侦察蜂阶段。

（1）初始化阶段：设定蜜源数量SN，问题维度D，最大迭代次数Gmax，允许最大失败尝试次数limit，然后根据如下公式随机初始化一组蜜源位置：

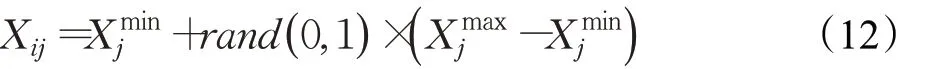
（2）雇佣蜂阶段：每只雇佣蜂占据一个蜜源Xi，并根据下式进行一维邻域搜索产生新的位置（候选蜜源）：

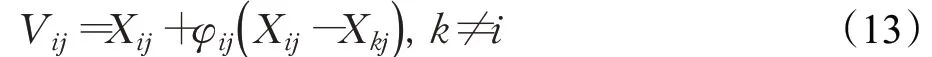
其中k∈{1,2,…,SN} ，j为随机选择的一个维度，φij是[-1,1]均匀分布的随机数[21-22]。所有雇佣蜂完成搜索后，通过摇摆舞[15]的方式向观察蜂传递蜜源位置及蜜源质量（适应度值）。

（3）观察蜂阶段：观察蜂根据雇佣蜂传递的信息按下式计算跟随每一个雇佣蜂的概率，随后采用轮盘赌来选择跟随对象，其概率计算公式如下：

其中fitness i表示第i个蜜源的适应度值，适应度值越大，表明该蜜源的质量越高，其被选择的概率也越大。而对于最小化问题，其函数值越小，蜜源越优秀，其适应度应越大，故须按下式转化：

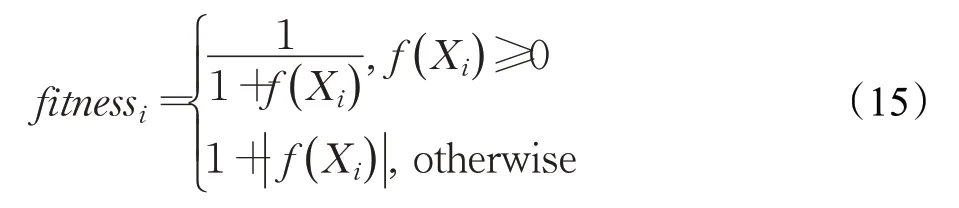
其中f(X i)即表示最小化问题的函数值，当其为非负数时应取其倒数，而为避免函数值趋于0适应度趋于无穷的情况发生，在其前加1后取倒；当其为负数时应取其绝对值，而对于最小化问题，负数显然比非负数更好，非负数最好的适应度为1，则负数的适应度应大于1，故在其绝对值前加1。

（4）侦察蜂阶段：若蜜源位置超过lim it次循环都没有更新，则雇佣蜂会放弃该蜜源转化为侦察蜂，按照公式（12）重新初始化。

2.2 基于边缘计算模型的编码调整

为使人工蜂群算法能够应用于边缘计算卸载问题，需要建立以下映射关系，以蜜源位置代表卸载决策，将寻找卸载决策的过程转化为人工蜂群算法寻找蜜源的过程，故需对人工蜂群算法进行离散处理。

假设移动终端数量为M，MEC服务器数量为N，云服务器数量为1，以0号位表示本地计算，1号位，2号位，…，N号位表示在对应编号的MEC服务器中卸载计算，N+1号位表示在云服务器中卸载计算。对初始化公式（12）进行离散处理得到：

其中randi(N+2)表示随机产生[1,N+2]上的整数，此时X ij即为在[0,N+1]的整数。每一个蜜源X i表示一个1行M列的卸载决策向量，向量中元素的数值即表示该设备需要将任务卸载的位置。

对位置更新公式（13）进行离散处理得到：

其中Y ij表示位移的增量，即位置更新公式中除Xij之外的其他项，[Y ij]表示对Y ij进行四舍五入取整，%为取余，对于公式（13）：

由于X ij和X kj均为[0,N+1]的整数，且φij在[-1,1]之间，故Y i j在[-N-1,N+1]之间。若[Y ij]=0，则表示仍然在原位置卸载，若[Y ij]＞0，则表示需要将该设备的计算位置向后移动[Y ij]位，然后对N+2取余，构造循环结构以保证更新后仍然为[0,N+1]的整数。若[Y ij]＜0则相应前移[Y i j]位，最终如公式（17）所示。

例如某一时刻有5个设备的任务需要卸载，有3台边缘服务器及一台云服务器。则以0表示本地计算，1、2、3分别表示在对应编号的边缘服务器计算，4表示在云服务器计算。

首先按式（16）初始化卸载决策向量（蜜源），假设其中一组卸载决策向量如图2的A图，即第一台设备将任务放在本地计算，第二台设备将任务卸载至云服务器计算，第三台设备将任务卸载至3号边缘服务器计算，第四台设备将任务卸载至2号边缘服务器计算，第五台设备将任务卸载至1号边缘服务器计算。假设在迭代过程中随机到第3维（第三台设备）进行更新，且[Y ij]=3，代入式（17），则更新后的卸载决策向量如图2的B图，第三台设备将会在1号边缘服务器计算。此时代入代价函数计算代价，择优选择，如果更新后的卸载决策更优则会替代原卸载决策。

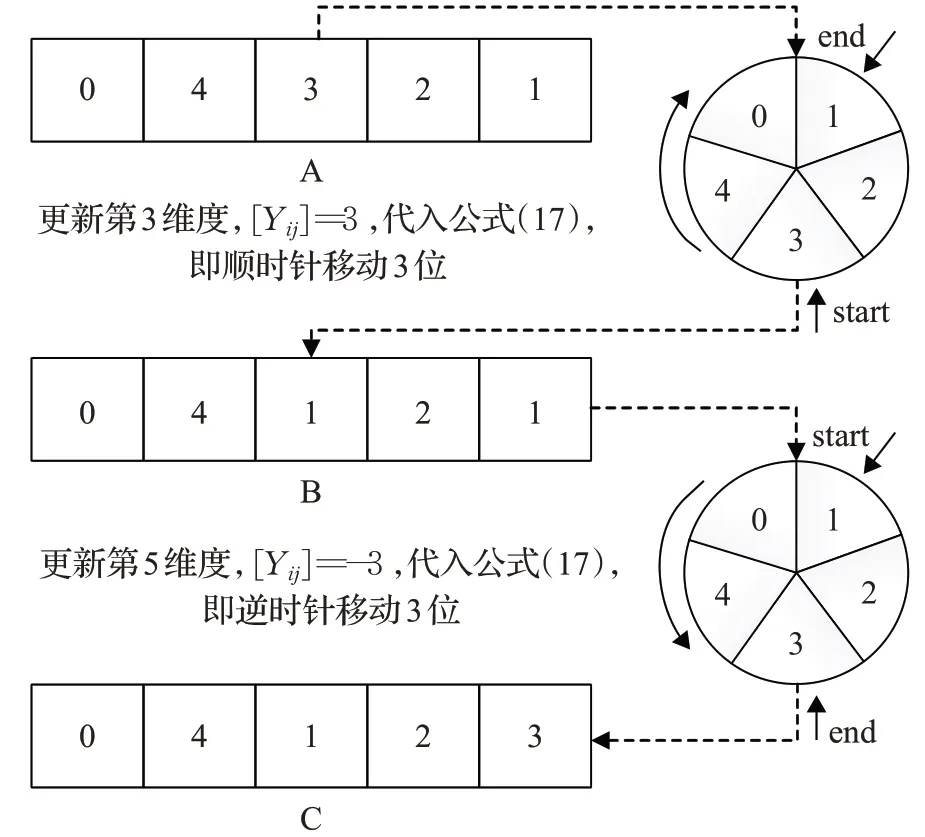
图2 位置更新演示Fig.2 Location update demo

假设在下一次迭代时，随机到第5维（第五台设备）更新，且[Y ij]=-3，代入式（17），则更新后的卸载决策向量如图2的C图，第五台设备将会把任务卸载至3号边缘服务器计算，后续的过程以此类推。

这样就完成了对人工蜂群算法的编码调整，使得其能够适用于本系统。

2.3 改进的人工蜂群算法

在MEC系统中，某一时刻需要卸载的任务数一般较多，对应的问题维度较高，针对高维复杂问题中人工蜂群算法收敛速度慢，开发能力弱的缺点，引入多维更新种群，利用种群优秀程度差异实现种群的转化，以此动态调整两种群规模。

2.3.1 单多维更新策略

为了平衡人工蜂群算法的探索与开发能力，并加快算法前期的收敛速度，在原有单维更新种群的基础上引入多维更新种群。

对于种群1在雇佣蜂和观察蜂阶段，采用一种精英引导的单维更新策略，文献[21]将全局最优解融入到搜索方程中提出了一种GABC算法，其位置更新公式如下：

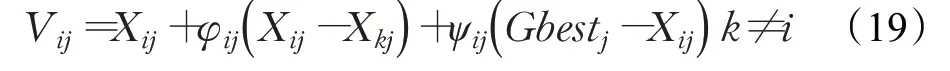
其中，Gbest j是全局最优个体的第j个元素，ψij是在[0,1.5]上均匀分布的随机数。

该算法取得了良好的收敛速度和收敛精度，但在复杂多模态问题上易陷入局部最优，本文将公式中的最优个体更改为精英个体，改进后的公式如下：

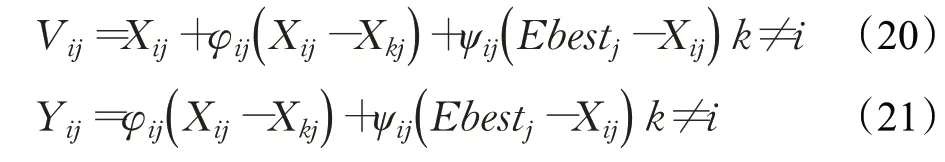
其中，Ebest j是从精英个体从随机选择的，定义种群中适应度前5的个体（最好的5个卸载决策向量）为精英个体。通过向精英个体的学习，在迭代前期，精英个体分布较为分散，有利于全局搜索，在迭代后期，精英个体较为集中，有利于局部搜索，提高收敛精度。

基本的人工蜂群算法迭代过程中都基于单一维度进行更新，而单维搜索策略也是限制ABC收敛速度以及后期收敛精度的主要原因，为了解决这一问题，对种群2在雇佣蜂阶段引入多维更新策略，观察蜂阶段仍使用式（13），更新的维度数设置为D up，按下式进行更新：

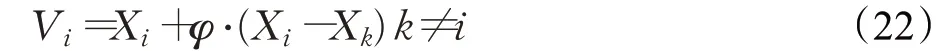
其中，φ是一个1行D列的矩阵，其中每一个元素都在[-1,1]之间，根据更新维度随机设置φ中D-Dup个元素为0，此时即表示更新Dup个维度，其余维度不更新，其中Dup会在执行动态种群策略时递减，·表示矩阵的点乘运算，Y ij的计算与公式（18）相同。

设定boundary为种群1和种群2的分界，两种群雇佣蜂总规模为SN，则编号1到boundary为种群1，boundary+1到SN为种群2，为保证在种群转化后，较差种群仍有一定的搜索能力，设定一个最小的种群规模Poplimit，在执行动态种群策略时两种群的规模都不得小于这一限制，在每一次迭代过程中其位置更新伪码如下：

1.fori=1∶boundary

2. 根据公式（17）和（21），生成新蜜源V i

3. iff(V i)＜f(X i)

4.Xi=V i；count(i)=0

5. else

6.count(i)=count(i)+1

7. end if

8. end for

9.根据公式（15）计算每一个个体的适应度值，并根据公式（14）计算每一个个体被选中的概率

10.form=1∶boundary

11.轮盘赌选择跟随对象，根据公式（17）和（21），更新位置并重复步骤3到7

12.end for

13.fori=boundary+1∶SN

14.随机选择D up个维度根据公式（17）和（18），生成新蜜源V i，并重复步骤3到7

15.end for

16.重复步骤9

17.form=bound ary+1∶SN

18.轮盘赌选择跟随对象，根据公式（17）和（18），更新位置信息并重复步骤3到7

19.end for

2.3.2 动态种群策略

设定种群优秀程度因子（degree of excellence，DOE）用于判断当前种群的好坏，DOE1和DOE2分别表示种群1和种群2的优秀程度。

在算法每一次迭代结束前进行评估，记录当前代最优个体的索引值index。

若index≤boundary，表明当前代最优个体在种群1中，种群1优秀程度增加，种群2优秀程度减小，即：

若ind ex＞boundary，则当前代最优个体在种群2中，种群2优秀程度增加，种群1优秀程度减小，即：

记录两种群优秀程度差异difference：

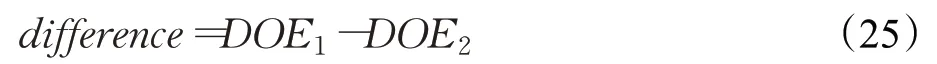
当 |difference|＞d limit时，认为两种群差异较大，此时执行种群转化，此处d lim it取1/4×Gmax。

对于最小化问题，不失一般性，若difference＞0，则表明单维更新种群1更优秀，此时将种群2的一部分转化为种群1。为最大化种群转化的收益，对种群2按目标函数值降序排序，此时种群2排在前面的个体即为较差个体，可以直接进行种群转化，即：

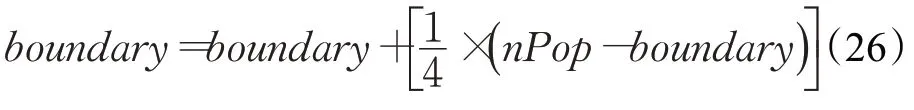
同理，若difference＜0，则表明多维更新种群2更优秀，此时将种群1的一部分转化为种群2，对种群1按目标函数值升序排序，此时种群1排在后面的个体即为较差个体，可以直接进行种群转化，即：

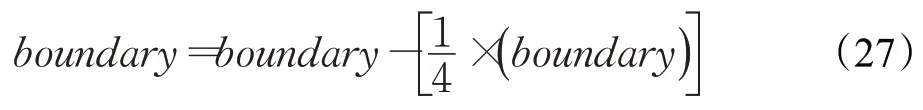
同时在每次转化过程中较差的种群需要向较好的种群进行学习，以保证较差种群在后续迭代过程的寻优能力。其学习策略如下：

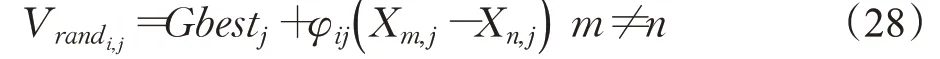
根据公式（17），则卸载模型中：

rand i为从较差种群中随机选择的一个个体，m、n为较好种群中随机的两个个体。伪代码如下：

1.ifind ex≤boundary

2.DOE1=DOE1+1；DOE2=DOE2-1；

3.else

4.DOE1=DOE1-1；DOE2=DOE2+1；

5.end if

6.diff er ence=DOE1-DOE2

7.if |difference|＞dlimit

8.DOE1=0；DOE2=0；

9. ifdifference＞0

10.Dup=round(0.8×Dup)

11. 对种群2按目标函数值降序排列，并根据公式（26）更新boundary

12. 从种群2中随机选择一个个体根据公式（17）、（29）、（30）向种群1学习

12.else

13. 对种群1按目标函数值升序排列，并根据公式（27）更新boundary

14. 从种群1中随机选择一个个体根据公式（17）、（29）、（30）向种群2学习

15.end if

16.end if

2.4 算法复杂度分析

文献[24]给出ABC算法一次迭代的时间复杂度为O(SN·D)，其中SN为蜜源数量，D为问题维度。与ABC算法相比，基于单多维动态种群策略的人工蜂群算法（artificial bee colony algorithm based on onedimensional and multi-dimensional dynamic population strategy，OMABC）在选择精英个体、多维更新以及动态种群转化时引入了额外的计算，为此给出本文算法的时间复杂度分析。OMABC在一次迭代过程中，选择精英解（对蜜源质量进行排序）的时间复杂度为O(SN·log(SN))，多维更新的时间复杂度为O(SN·D)，动态种群转化（对较差种群的蜜源质量进行排序）的时间复杂度为O(S N·log(SN))，则本文算法的时间度为O(SN·D+SN·log(SN))，而针对高维复杂问题，D通常远大于log(SN)，故改进算法的时间复杂度可简化为O(SN·D)与ABC算法时间复杂度相同。

2.5 有效性验证

为验证该算法在高维问题上的有效性，使用IEEE CEC 2017中29个测试函数分别在50维、100维进行实验，其中F1、F3为单峰函数，F2因不稳定已被CEC官方删除，F4～F10为简单多峰函数，F11～F20为混合函数，F21～F30为复合函数。算法寻优结果越接近各测试函数最优值，表明算法寻优能力越强。

将OMABC与经典最优引导改进算法GABC[21]、ABC/best/1[22]和近些年提出多策略混合算法Modified-ABC[23]、MHABC[24]，进行对比实验。实验环境：处理器AMD Ryzen 7-4700U CPU@2.0 GHz，RAM 16 GB，Windows10 64位操作系统，MATLAB R2018b。设置50维时Gmax=5 000次，100维时Gmax=8 000次，为保证公平，采用统一方式初始化，每个算法独立求解29个测试函数，并记录最终寻优结果。重复上述过程30次，计算各算法在29个测试函数上最终寻优结果的平均值及标准差。OMABC的具体实现步骤如下：

1.初始化算法参数，包括SN、D、Gmax、limit、boundary等；

2.根据公式（12）初始化蜜源；

3.按单多维更新策略伪代码部分，使用式（20）和（22）完成雇佣蜂阶段及观察蜂阶段；

4.若蜜源连续limit次都没有得到更新，则雇佣蜂放弃该蜜源转化为侦察蜂按式（12）重新初始化；

5.按动态种群策略部分伪代码实现种群转化，较差种群通过式（28）向较好种群学习；

6.记录全局最优值，判断是否满足算法终止条件（是否达到最大迭代次数），若满足，则返回最优结果，否则返回步骤3继续迭代。

得到的结果如表1、2所示，加粗部分为最优值，表中存在数值相同但未被加粗的情况，这是因为数据采用科学计数法统计时存在四舍五入的情况，其真实值会略大于加粗值。实验结果表明，在50维时OMACB在15个测试函数取得最好的收敛的精度。除在F26、F30两个测试函数外，OMABC的表现均比原始的ABC效果优异，在F4、F5、F7、F8、F16、F20、F21、F22、F25、F28、F30上与对比算法相差不大。

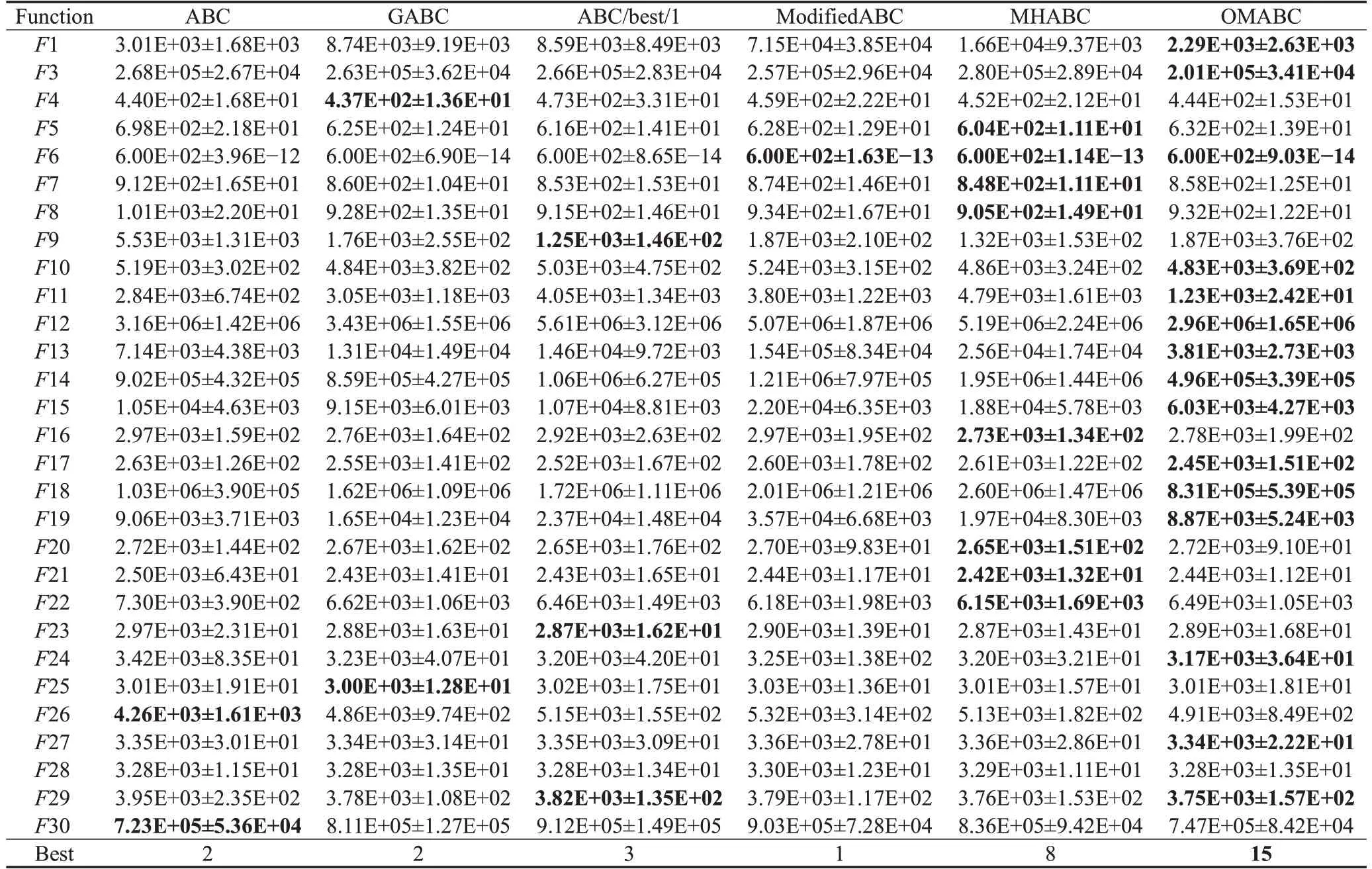
表1 50维ABC及其变种算法结果比较（平均值±标准差）Table 1 Comparison of 50-dimensional ABC and its variant algorithm results（mean±std.）

而在100维时，29个测试函数的收敛精度均超过基本的ABC。这是因为，基本ABC的单维更新方式难以在高维问题上发挥作用，而OMABC的单维与多维更新相互配合的方式，更能适应高维复杂问题，最终在16个测试函数上取得最优，在F4、F8、F16、F20、F23、F24、F27、F28上与对比算法差距不大。这说明单多维动态种群策略的确能够提高的算法的寻优能力，且在高维问题上更有优势。

图3为在100维的测试函数F1中OMABC单维更新种群的种群规模变化曲线及ABC与OMABC的收敛曲线，其中虚线boundary表示种群1的种群规模，可以看到在迭代前期，单维更新种群表现更为优异，OMABC会相应的扩大单维更新种群的规模，同时由于采用了精英引导策略，在迭代速度方面有更多的优势，而在迭代后期，单一维度的更新已经无法满足算法跳出局部最优的需要，此时多维更新种群的表现更好，更多的个体将执行多维更新策略，帮助算法跳出局部最优，并提高收敛精度。

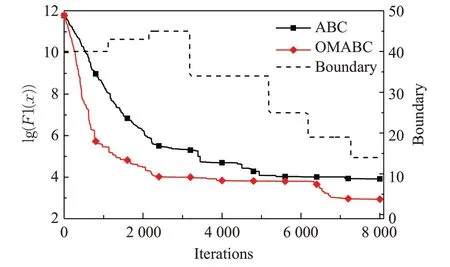
图3 收敛曲线及种群1规模变化曲线Fig.3 Convergence curve and populationa 1 boundary change curve

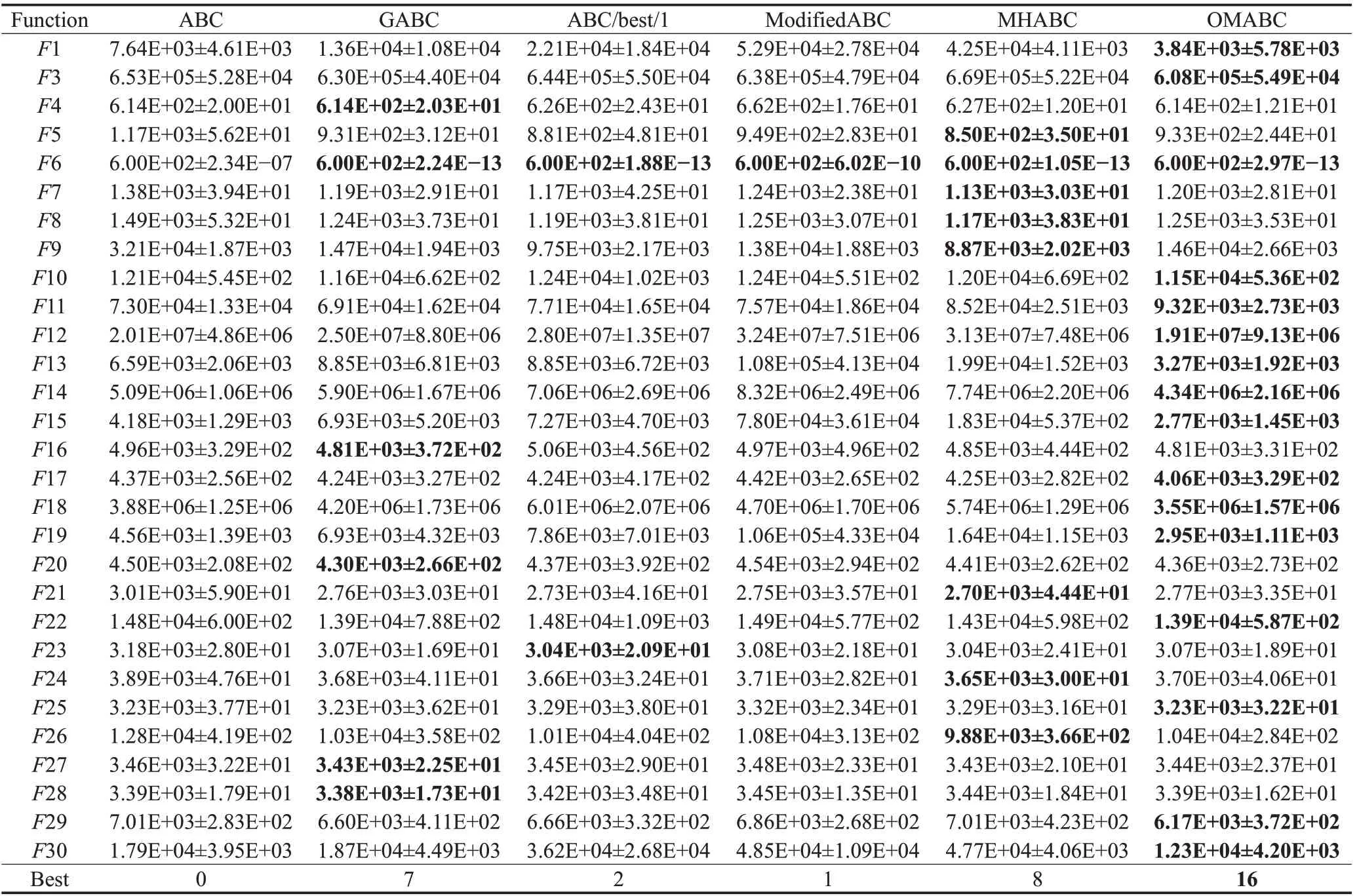
表2 100维ABC及其变种算法结果比较（平均值±标准差）Table 2 Comparison of 100-dimensional ABC and its variant algorithm results（mean±std.）

3 仿真实验

3.1 参数设置及算法流程

在验证改进策略有效性后，将OMABC算法应用于第1节的MEC系统模型上仿真。

同样选择在处理器AMD Ryzen 7-4700U CPU@2.0 GHz RAM 16 GB，Windows 10 64位操作系统下使用MATLAB R2018b进行实验。

MEC系统各项参数设置为：移动设备个数M={50,100,150,200,250,300}，MEC服务器个数N=10，云服务器个数为1，算法最大迭代次数设置Gmax=100，其他参数设置如表3。

表3 MEC系统参数设置Table 3 MEC system parameters setting

PSO算法参数：nPop=50，c1=c2=1.5，ω=0.5；ABC算法参数设置为：SN=50，limit=100；OMABC算法参数设置为：SN=50，limi t=100，D up=0.8×M，boundary=4/5×SN。

在设置好系统各项参数后，还需要确定代价函数中惩罚系数g的取值。由于T与E的量纲、数量级存在差异，故需根据实验条件设置合适的g以平衡代价函数中时延与能耗的关系。当任务全部在本地卸载时，会对移动设备的性能有较高的要求且会带来相当高的能耗，减少移动设备使用时间，此时代价函数应该有一个相当高的代价。

当任务全部在服务器上卸载时，将会获得一个较低的能耗和较高的时延，也应有一个较高的代价。这两个代价应尽可能的接近，以使得卸载算法能够得到合理的卸载决策。此处采用二分法确定g的取值范围，起始时设置g分别为0和1，随机设置30组全部在本地卸载与30组全部不在本地卸载的决策向量，代入代价函数后获取其平均值。随后逐步缩小g的范围至[0，0.5]、[0，0.25]、[0，0.125]一直到[0.046 875，0.050 781 25]附近时两代价曲线已几乎重合，限于篇幅仅展示部分曲线如图4所示，故确定g的范围应在0.050 781 25附近，此值可根据实际情况自行调整其大小，当希望能耗影响更大时适当取较大值，当希望时延影响更大时则取较小的值，此处取g=0.05以使得时延与能耗具有相近的影响。确定好惩罚系数g的取值后即可开始仿真实验，OMABC的具体卸载流程如图5所示。

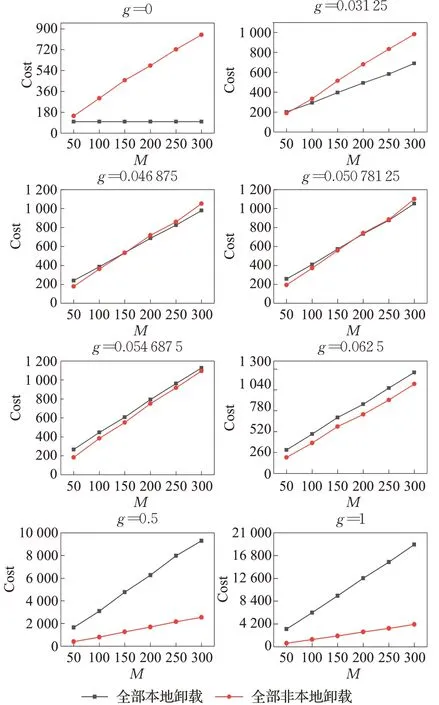
图4 不同g时的代价曲线Fig.4 Cost curve at different g

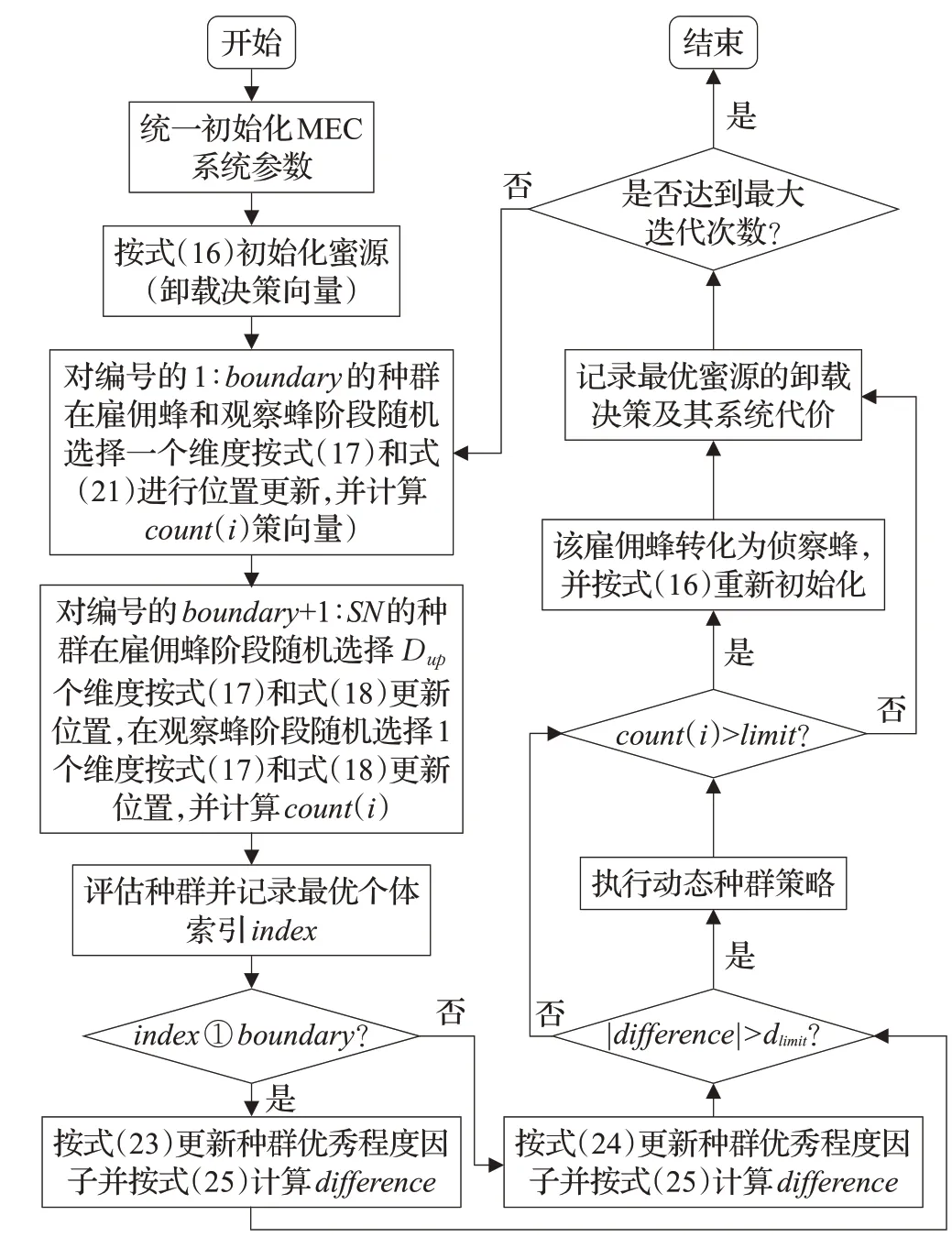
图5 算法流程图Fig.5 Algorithm flow chart

3.2 结果分析

在上述参数设置下，独立重复实验30次，选择随机卸载算法（Random）、粒子群算法（PSO）、基本的人工蜂群算法（ABC）与本文的改进算法（OMABC）进行对比。

图6为在迭代次数均为100次时，不同卸载算法的收敛曲线，为保证实验公平，所有算法统一初始化位置。

图6 不同卸载算法的收敛曲线图Fig.6 Convergence curves of different offloading algorithms

可以观察到，各种卸载算法在前20次迭代中都有较快的收敛速度；Random算法，由于采用随机卸载策略，具有盲目性，在M为50时尚能依赖随机性寻优，但在更高维度（150维度及以上）时，已几乎趋于直线，丧失寻优能力。这是由于高维问题更为复杂，随机寻找缺乏目标，有利维度的信息无法保留导致的。

PSO算法通过向个体最优以及全局最优学习，在前10次迭代中取得了更好的表现，在M为50、100、150、250、300时具有较快的收敛速度，超过了基于的ABC的卸载算法；观察PSO的迭代曲线不难发现，粒子群算法由于每次位置更新均为全维度更新，迭代曲线呈现阶梯状，这就对算法的迭代次数有很高的要求，需要设置合适的迭代次数以最大化收益，且由于其没有跳出局部最优的操作，算法后期也很难跳出局部最优位置。

ABC算法则有较为平滑的迭代曲线，没有明显的阶梯状，这是由算法的单维更新策略以及侦察蜂阶段所保证的，算法一维一维的缓慢向最优位置附近挪动，有效利用了优秀位置的维度信息，且不易陷入局部最优，能够较为平稳的寻优。同时单维更新策略也是制约算法在高维问题上收敛速度的主要因素，如在M为250、300时，算法在第30次迭代后寻优精度才高过PSO算法。

而OMABC除拥有较强跳出局部最优的能力外，还具有较快的收敛速度，在迭代后期仍具备较强的寻优能力，这是由于OMABC采用了动态种群策略以及精英引导学习，能够自适应判断种群的好坏从而实现单维更新种群以及多维更新种群之间的相互转换，平衡算法的探索和开发能力，提高收敛速度和收敛精度。在迭代前期，两种群经历一定时间的独立寻优后，能够自适应的扩大优秀种群的规模，从而加快算法前期收敛速度。在迭代后期，OMABC又具有人工蜂群算法不易陷入局部最优的良好性质，同时又可以自适应的判断当前寻优的状态，若距离最优位置较近，则扩大单维更新种群，提高收敛精度；若所处位置为局部最优位置，则扩大多维更新种群，进一步提高算法跳出局部最优的能力。

从图6中可以看出M=50时，Random算法优化后系统总代价降低了7.43%，PSO算法优化后系统总代价降低了12.37%，ABC算法优化后系统总代价降低了18.76%，OMABC算法优化后系统总代价降低了21.60%。

在M=100时，Random算法优化后系统总代价降低了1.85%，PSO算法优化后系统总代价降低了9.61%，ABC算法优化后系统总代价降低了15.80%，OMABC算法优化后系统总代价降低了18.28%。

在M=150时，Random算法优化后系统总代价降低了0.21%，PSO算法优化后系统总代价降低了5.81%，ABC算法优化后系统总代价降低了10.79%，OMABC算法优化后系统总代价降低了11.29%。

在M=200时，Random算法优化后系统总代价降低了1.86%，PSO算法优化后系统总代价降低了8.66%，ABC算法优化后系统总代价降低了10.98%，OMABC算法优化后系统总代价降低了12.53%。

在M=250时，Random算法优化后系统总代价降低了2.25%，PSO算法优化后系统总代价降低了9.20%，ABC算法优化后系统总代价降低了11.71%，OMABC算法优化后系统总代价降低了14.29%。

在M=300时，Random算法优化后系统总代价降低了1.13%，PSO算法优化后系统总代价降低了7.55%，ABC算法优化后系统总代价降低了9.45%，OMABC算法优化后系统总代价降低了11.16%。

除M=50外，其他情况下各算法降低的代价都相对稳定，这是由于50维的问题较为简单，各算法均能获得更好的解，而其他情况下问题维度更高，寻优难度提升导致的。同时，不难看出OMABC在各情况均取得了最好的效果。

如图7为在相同的迭代次数下独立运行30次得到的箱线图，箱体中位线表示算法30次运行的中位数，反应了数据的一般水平，箱体的上下边界称为内限，分别表示数据的上四分位和下四分位，因此箱体的宽度可以在一定程度上反应算法的稳定性。超出箱体上方和下方的之外的界限称为外限，分别表示样本数据剔除异常值后的最大值和最小值（1.5 IQR内的范围）。

图7 不同卸载算法的箱线图Fig.7 Box plots of different offloading algorithms

可以看出OMABC算法，在设备数为50、100、150、200、300时箱体宽度均比对比算法小，具有较好的稳定性，在设备数为250时，OMABC的箱体宽度与ABC近似，表明稳定性与ABC算法近似。综上可以证明OMABC在解决此类问题上具有较好的稳定性。从整体上看，OMABC箱体所处位置较其他算法更低具有较好的收敛精度。

如图8为在不同设备个数的情况下，30次独立运行后不同卸载策略的平均代价柱状图，其中Local表示在本地计算。实验中设备个数M分别为50、100、150、200、250、300，可以观察到随着设备数量的增加本地卸载策略的系统总代价增加较为明显，这是任务数量增多而又没有得到有效卸载导致的。采用Random、PSO、ABC、OMABC算法卸载后的系统总代价较本地计算更低，减少了系统的时延与能耗。

图8 不同设备数下各算法代价Fig.8 Cost of each algorithm under different M

OMABC与本地计算的差异也随着设备数的增加在逐渐增大，在M为50时，系统代价平均降低了113.87；M为100时，系统代价平均降低了134.02；M为150时，系统代价平均降低了153.95；M为200时，系统代价平均降低了170.49；M为250时，系统代价平均降低了199.39；M为300时，系统代价平均降低了218.86；在不同设备数M下均能取得更为优秀的效果，验证了OMABC算法在解决此类问题上的优越性。

4 结束语

本文针对多设备MEC系统中计算任务的执行时间以及终端设备的能耗最小化问题，构建了一个云服务器辅助的多MEC服务器计算卸载模型，并提出了一种改进的人工蜂群算法（OMABC），通过单维更新种群和多维更新种群的相互转化与配合，提高算法的收敛精度，并在CEC 2017进行测试，验证了算法的有效性。通过添加惩罚因子，设计代价函数，将OMABC运用在移动边缘计算卸载问题上，实现了在能耗约束下最小化时延的目标。仿真结果表明，与Random、PSO、ABC相比，本文的OMABC算法具有更好的卸载性能。未来的研究将进一步优化人工蜂群算法，考虑任务的前驱和后继结点，将其运用在MEC中基于工作流的任务卸载问题上。