模糊随机碰撞工作量证明共识算法

廖浩德，邹晓凤，王 兵，肖辞源

1.西南石油大学 计算机科学学院，成都 610500

2.成都川链大数据研究中心，成都 610500

2008年，在发表名为《比特币：一种点对点式的电子现金系统》论文中，首次提出了区块链（blockchain）这一概念[1]。区块链也称为价值互联网[2]，本质上是一个去中心化的分布式数据库，是密码学、共识算法、点对点网络等多种技术的融合创新。区块链通过共识机制，实现区块链系统中节点数据一致，共识算法则是实现这一目标的核心要素。

根据应用场景不同，区块链分为公有链、私有链、联盟链[3]。私有链的写入权限归属于某个组织和机构，其网络系统中的参与节点会被严格限制。联盟链中节点数量较为固定，分为记账节点和其他节点。其中记账节点由群体内部事先指定，记账节点共同决定链上每个区块的生成，其他节点可以参与交易，但不过问记账过程。联盟链的共识算法分为拜占庭容错共识算法和非拜占庭容错共识算法，前者的典型共识算法有实用拜占庭容错（PBFT）[4]、HotStuffBFT[5]等；后者的典型共识算法有Paxos[6]、Raft[7]等。相对于私有链和联盟链，公有链是目前应用最广泛的区块链。

公有链系统允许所有参与节点对其数据进行读写、并可以自由进出，其典型的共识机制包括工作量证明（PoW）[8]、权益证明（PoS）[9]、股份授权证明（DPoS）[10]等算法。其中，PoW算法作为较为成熟的共识技术被应用于比特币、以太坊等公有链。但在实际应用中存在一些急需解决的问题，例如，高速计算机或量子计算机的出现将导致PoW所使用的加密算法难以保证其安全性[11]，对算力也难以调控。进一步提高区块链的安全性，对高速计算机算力的调控等都是当前区块链研究的热点。

本文针对共识算法存在的安全性和算力难调控等问题，提出了基于模糊数学方法的新共识算法，该算法通过引进模糊传递闭包阵等技术，增大其解空间解决安全性问题，还采用双重调节机制解决算力难调控问题。

1 相关背景知识介绍

1.1 PoW共识算法

区块链本质上是一个分布式存储系统，该系统主要任务是如何实现网络中节点之间的共识。以比特币和以太坊中的PoW为例。比特币系统中的节点通过与或运算，寻找一个满足特定条件的随机数值（nonce），即可获得本次区块的打包权，广播本轮需要记录的数据，在全网节点验证成功后再一起存储区块信息[12]；在以太坊系统中节点需要找到的不只是nonce值，还需计算Mix-Digest值，当找到满足条件的nonce值后，会将计算出来的digest值赋给MixDigest，并存储于区块头作为后续区块验证的条件，最后完成区块信息广播、全网验证存储。共识旨在防止恶意节点操作区块链，从而保证数据的完整性。图1、2分别为比特币系统和以太坊系统中PoW共识算法工作框图。

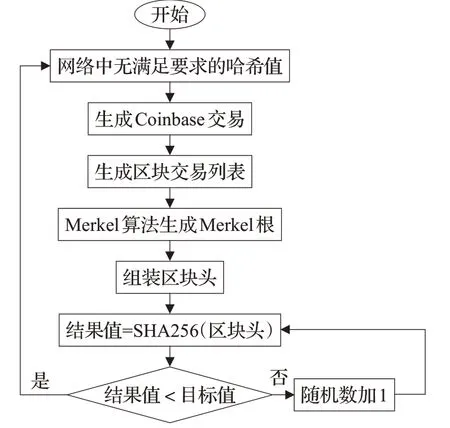
图1 比特币PoW共识算法工作框图Fig.1 Block diagram of Bitcoin PoW consensus algorithm

根据图1、2可知，两个算法过程都是通过不停变化区块头及其附带的随机数作为输入，再通过SHA-256计算，得到一个特定格式哈希值（即要求该哈希值的前p位为0）[13]。哈希值前置0的个数越多，代表区块难度越大。其中，SHA-256加密算法主要用于完成交易数据的认证，保证交易数据的完整性以及数字签名的验证，保证了系统中交易数据不可篡改。SHA-256加密后得到一个前置p位为0的256位哈希值，则其解空间为2256。以不变的SHA-256算法的解空间来应对算力不断增加的高速计算机乃至量子计算机，将无法保证PoW算法的安全性。

1.2 模糊传递闭包阵

在1965年，美国控制论专家Zadeh教授发表了《Fuzzy Sets》[14]一文；为模糊数学奠定了基础。这一开创性的工作在软、硬科学中为提高数学适用性开辟了广阔途径。其中本文用到的模糊传递闭包阵等相关知识定义如下[15]。

定义1r ij∈[0,1](i=1,2,…,m;j=1,2,…,n)，矩阵R=(r ij)m×n称为m×n阶的模糊矩阵。

定义2m=n且RT=R时，R为模糊对称矩阵。

定义3包含R而又被任一包含R的传递矩阵所包含的传递矩阵，称为R的传递闭包t(R)。计算t(R)的过程采用乘法公式：

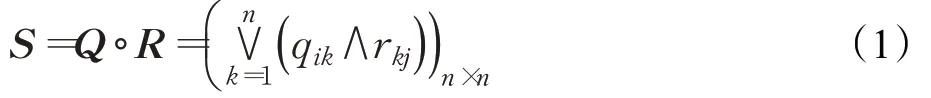
其中“∘”表示软代数计算算子。Q表示n×n阶模糊矩阵，R表示n×n阶模糊矩阵，S表示两个模糊矩阵的乘积，qik表示模糊矩阵Q的元素，r kj表示模糊矩阵R的元素，通过公式（1）得到两个矩阵的相乘矩阵，再通过幂算法公式：

求得R的模糊传递闭包阵t(R)，其中：

并具有特性：

定理1求t(R)过程经过n4次的取∨和∧运算。

证明R 2=R∘R≜(s ij)n×n，其中1,2,…,n;j=1,2,…,n)。

（1）对于固定i,j=1,2,…,n：q ik∧r kj为n次∧运算；

（2）对于i=1,2,…,n时，则共有n2次∧运算；

（3）对于k=1,2,…,n时，共有n次取∨运算；

综上三点可知则对于公式（1）的矩阵乘法运算可知R∘R共有n×n2=n3次(∨,∧)运算。（4）通过公式（2）和（3）可知，求t(R)过程共有n次矩阵相乘运算。

综上四点可知求t(R)模糊传递闭包阵有n×n3=n4次运算，证毕。

2 FRMH算法设计

随着计算机运算速度的不断提升，以不变的解空间应对高速计算机，理论上PoW的加密算法终将被破解。本文的新共识算法则引入了模糊传递闭包阵与哈希加密结合实现二次加密、再通过随机数碰撞得到满足条件的哈希值，来提升共识算法的安全性。本创新算法命名为模糊随机碰撞工作量证明共识算法，又称FRMH共识算法。

FRMH共识算法是利用种子和区块头哈希作为输入、再操作随机数获得满足难度且通过验证的区块进而完成整个算法。其中种子由上一区块中的n、p、H构成，n为模糊传递闭包阵的阶数、p为哈希值前置0的个数、H为上一区块随机数的值。FRMH共识算法主要包括：构造矩阵、运算矩阵、工作生成、工作验证四个阶段。

2.1 构造矩阵

FRMH共识算法的技术创新是首次将模糊传递闭包阵引入到共识算法。为了得到满足要求的传递闭包阵，首要任务则是构造出一个n阶模糊对称阵。主要步骤如下：

（1）生成模糊对称阵

由种子生成一个行列向量线性无关的n阶模糊对称阵R。

（2）求R的模糊传递闭包阵

通过上文中的公式（1）和（2）计算得到R的模糊传递闭包阵t(R)

此处求得传递闭包矩阵t(R)是单向不可逆过程，符合区块链哈希加密正向快速、逆向困难的特点。

2.2 运算矩阵

通过S加密算法对公式（2）求得的模糊传递闭包阵t(R)进行加密运算，得到一个32字节长度的值f，其中：

2.3 工作生成

使用与运算矩阵阶段相同的S加密算法对f和区块头进行加密运算，也得到一个长度为32字节的值hf，其中：

2.4 工作验证

验证节点是否完成工作，就是对节点的工作价值和区块难度进行比较。由于FRMH共识算法中使用的S加密算法为SHA256加密算法，节点工作验证则是判断hf的256位哈希值前置0的个数是否等于种子中p值。如若不相等表示工作验证不成功，则将工作生成阶段S加密运算后生成的nonce值赋予H，开始新一轮的计算过程。验证成功后，节点则将在其他人广播之前广播该区块。

2.5 解空间

FRMH共识算法在运算过程中分为求解模糊传递闭包阵和哈希运算两个过程。

（1）求传递闭包阵

公式（1）是幂算法求t(R)的中间过程。通过定理1可知此过程计算次数为n4，则此过程的解空间为n4。

（2）加密运算

加密运算过程采用SHA256加密算法对区块头和模糊传递闭包阵加密值进行运算，则其解空间为2256。

综上两个步骤计算结果，得到FRMH共识算法解空间为n4×2256。

2.6 难度调节

FRMH共识算法通过模糊传递闭包矩阵的阶数n和哈希值前置0的个数p对区块难度进行调节。本实验硬件采用4核8线程的Intel Core i7-7700HQ处理器，8 GB内存的硬件平台。通过搭建gen私链得到如图3所示的算力模拟曲线。

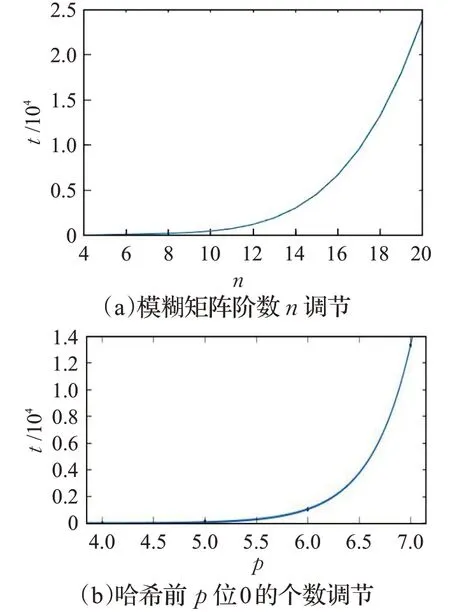
图3 算力测试模拟曲线Fig.3 Simulation curve of computing power test

图中模糊矩阵的阶数n和哈希值前置0的个数p是随算力的大小自动调节，分为线性调节和几何调节。主要分为以下几种情况。

（1）当p＜256时

①线性调节：

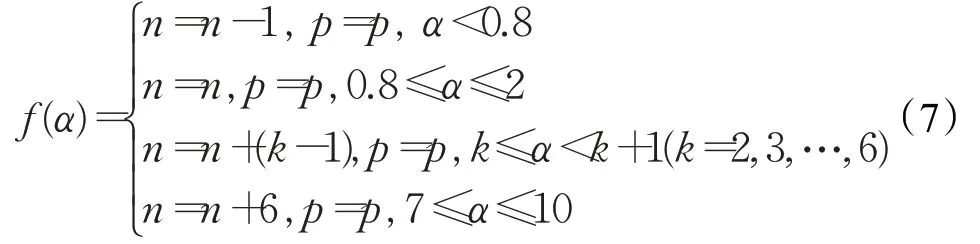
②几何调节：

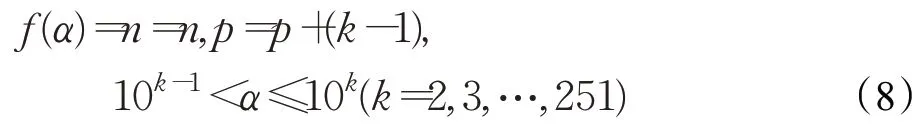
（2）当p=256时

①线性调节：

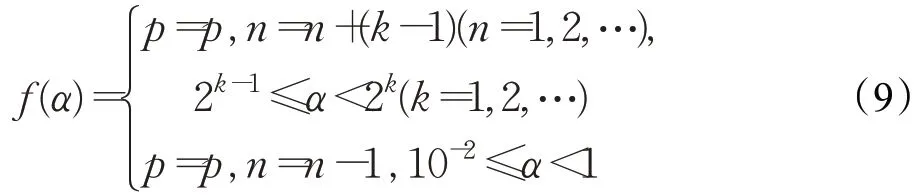
②几何调节：

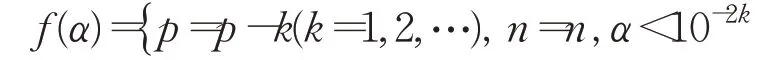
其中α为难度系数，通过α=10÷(t-t0)计算（t0=上一区块时间，t=本区块时间）。

2.7 FRMH算法实现

（1）根据FRMH共识算法的4个阶段构建出算法框架图，如图4所示。

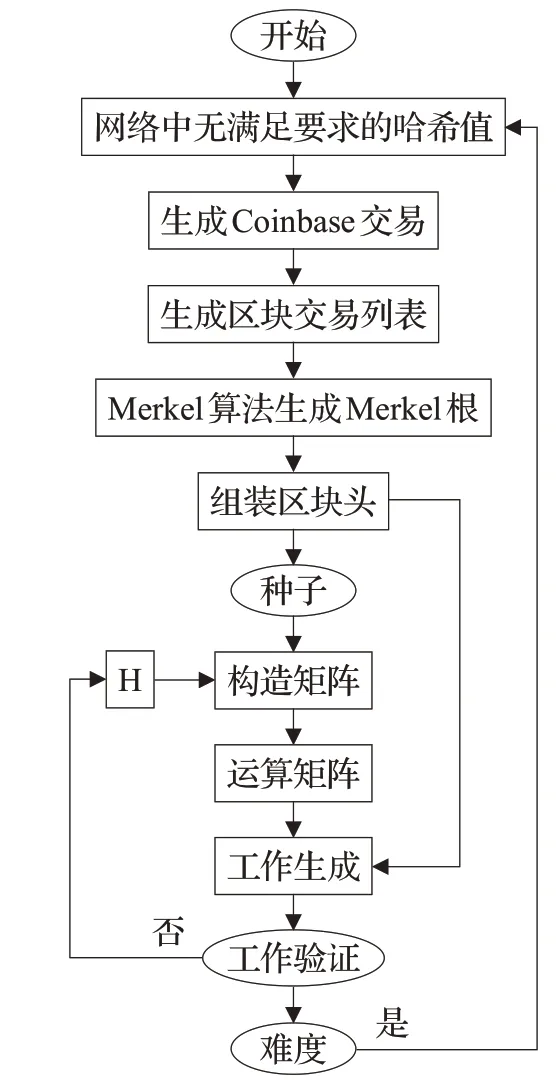
图4 FRMH算法框架Fig.4 FRMH algorithm framework

根据图1和图2两个算法框图可知，FRMH共识算法在组装区块头时相对于PoW共识算法增加了变量矩阵阶数n；运算过程中增加了对矩阵的计算。FRMH共识算法的难度调节是根据双重调节机制进行的，即同时改变n（n可无穷大）、p（最多256位）值；而PoW共识算法则是根据最新2 016个区块的出块时间调节难度，即只改变p值。但FRMH共识算法引入的变量n，n的变化体现了对高算力调控的优势。

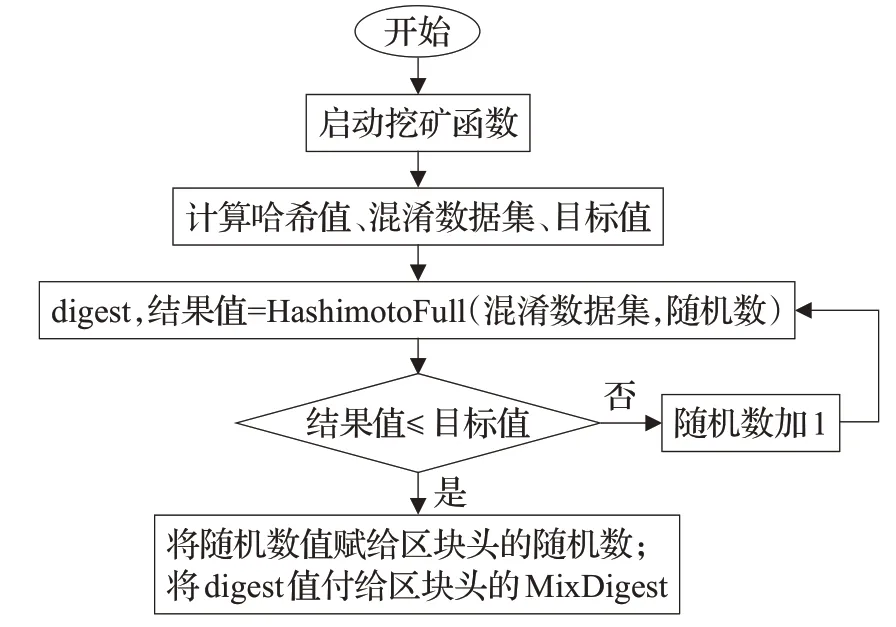
图2 以太坊PoW共识算法工作框图Fig.2 Ethereum PoW consensus algorithm working block diagram

（2）go语言实现FRMH共识算法构造矩阵、运算矩阵、工作生成3个过程，如算法1～3所示。

算法1构造矩阵

Input：n、p、H-a byte array of 64

Output：M-ann-order matrix

InitializeN=int(n)

InitializeP=int(p)

M:=InitMatrix(N,N)

fori=1;i＜=N;i++{f

orj=i;j＜=N;j++{

if(i==j){//生成模糊矩阵主对角元素

M.Set(i,j,1)

}else{//不满足条件重新生成模糊矩阵

xx:=GetElement(N,P,nonce,i,j)

M.Set(i,j,xx)

}

}

}

fori=1;i＜=N;i++{//生成模糊矩阵上下三角元素

forj=i+1;j＜=N;j++{

M.Set(j,i,M.Get(i,j))

}

}

count:=int（math.Log2（float64（N）））；//模糊矩阵计算

Fori=0;i＜=count+1;i++

M=FMultiply(M,M);

returnM；

算法2运算矩阵

Input：matrixString is the string converted byM

Output：32-byte cryptographic Hash ofM

matrixString：=M.ToString()//获取矩阵字符串

f:=S（matrixString）

returnf；

算法3工作生成

Input：fhash and blockHead are 256-byte strings

Output：hfis a 256-bit Hash value

fhash:=f.ToString（）//得到矩阵的散列

hf=S（fhash+blockHead）

returnhf；

（3）针对FRMH共识算法解空间问题，当n=6时，FRMH共识算法解空间为64×2256，PoW共识算法解空间为2256，FRMH共识算法是PoW共识算法的1 296倍，大幅度提高了区块链的安全性。

3 FRMH算法评估

（1）FRMH共识算法大幅度地提高了区块链的安全性能

由表1可知比特币和以太坊算法都是运用哈希加密算法，解空间为2256，其计算碰撞需要248年[16]，一般的普通电脑要破解其加密算法几乎是不可能的，这就是区块链至今未被攻破的原因。但是1台量子计算机约相当于105台普通电脑的算力[17]，如用量子计算机来破解哈希加密算法完全没有问题。量子计算机的出现将使得哈希加密算法失效，现有的区块链技术就失去了意义[18]。而FRMH共识算法的双重加密算法解空间为n4×2256，大幅度提高了区块链系统的安全性，且随着n的增大，其安全性能呈几何级数的增长。

表1 FRMH算法与主流共识算法解空间比较Table 1 FRMH algorithm and mainstream consensus algorithm solution space comparison

（2）FRMH共识算法可抵抗高算力计算机的攻击

由表2可知，比特币和以太坊算法都是通过p值对区块的计算难度进行调节，且调节范围是0～256；FRMH共识算法通过模糊矩阵的阶数n和哈希值前置0的个数p实现了双重调节，其中，p的取值范围是0～256，但n的取值范围却是无限的。量子计算机运算速度再快亦是有限的，从理论上讲用无限抵抗有限总是可行的。

表2 FRMH算法与主流共识算法难度调节比较Table 2 FRMH algorithm and mainstream consensus algorithm difficulty adjustment comparison

4 结束语

共识机制是区块链节点数据一致性的重要保证。现有的PoW共识算法存在安全性和高算力难调控两个缺点。本文提出的基于模糊数学方法的FRMH共识算法解决了高算力计算机乃至未来量子计算机给区块链带来的安全性问题。

FRMH共识算法融入了模糊传递闭包阵等技术，通过模糊传递闭包阵阶数的变化，将解空间提升为n4×2256，大幅度提高了区块链的安全性；该算法采用双重调节机制（线性调节与几何调节），用无限抵抗有限，实现了可抗高算力计算机，乃至未来的量子计算机的攻击。下一步，可以对FRMH共识算法进行优化设计研究，进一步改善gen链上的出块时间问题，进而加快链上的交易速度，并将FRMH共识算法应用于更多的公有链，给区块链发展带来更大的空间。