高电缆化率下谐波源谐波发射水平评估方法
潘玲,冯倩,张鹏 ,沈冰,周健,陈冉,赵劲帅
(1.国网上海市电力公司电力科学研究院,上海 200437;2.四川大学电气工程学院,四川 成都 610065)
近年来,城市电网的电力电子化率逐步提升,加剧了谐波源的复杂性与多样性,谐波污染变得愈加严重[1]。对于电网中谐波电压含量较高的母线,有必要准确量化系统侧与用户侧的谐波发射水平,进而追溯主导谐波源,指导谐波治理。
计算谐波阻抗是评估谐波发射水平的关键,现有计算方法的原理主要基于两点假设:1)背景谐波相对稳定;2)用户侧谐波阻抗远大于系统侧谐波阻抗,从而可将其忽略,只需计算系统侧谐波阻抗即可完成谐波发射水平评估[2-7]。例如,波动量法[2-3]与一系列回归法[4-5]在背景谐波波动较小时具有较好的计算精度,但当背景谐波波动剧烈时计算误差显著增大。独立随机矢量协方差法[6]基于用户侧谐波阻抗远大于系统侧的前提,认为公共线路上流过的谐波电流与背景谐波弱相关,可在一定程度上抑制背景谐波波动对计算的影响,但当所需前提不成立时计算精度较低。此外,快速独立分量分析(fast independent component analysis,FastICA)[7-10]法理论上只需利用两侧谐波源信号快变分量的独立性即可重构源信号,进而求解谐波阻抗,具有较强的抗背景谐波波动的能力。但在实际应用中,当两侧谐波阻抗幅值较接近时,其计算误差较大。
通常而言,现有方法所需的上述两点假设对传统非线性用户成立,但随着城市电网电力电子化率以及电缆化率的不断提升,一方面,系统侧包含大量的非线性用户谐波源,加剧了背景谐波的不稳定性;另一方面,电缆的对地电容较大,可能与电网中其他感性元件发生感容耦合,使得在某些频次下,系统侧谐波阻抗增大,且不再远小于用户侧谐波阻抗[11-12]。从而,现有方法所需假设不再成立,需寻求新的求解方法。
除此之外,现有方法大多只能计算系统侧谐波阻抗,但在城市电网中,考虑到系统侧谐波阻抗受高电缆化率影响而在某些频次下增大,公共连接点(point of common coupling,PCC)两侧谐波阻抗可能较为接近,需同时计算系统侧与用户侧谐波阻抗才能量化谐波发射水平,从而为评估工作带来新的挑战。
尽管FastICA算法理论上可计算PCC点两侧的谐波阻抗,但在高电缆化率城市电网的上述工况中,计算误差较大。为此,本文结合中心极限定理分析现有FastICA算法误差来源,进而将其与新兴的盲源分离技术稀疏成分分析法(sparse component analysis,SCA)[13-14]相结合,提出改进FastICA算法。该算法以“全局-局部-全局”作为源信号的分离思路,在FastICA分离所得信号附近进行局部搜索,引入稀疏筛选与综合负熵筛选机制,得到与真实源信号吻合的局部信号,进而求取两侧谐波阻抗,并评估谐波发射水平。当背景谐波较大且两侧谐波阻抗接近时,所提改进FastICA算法均能准确评估谐波发射水平。仿真与实际工程案例验证了该方法的有效性。
1 谐波发射水平评估模型
对于城市电网中谐波电压含量较高的母线,将电网分为系统侧与用户侧,其诺顿等效模型如图1所示。

图1 谐波发射水平分析原理图Fig.1 The model of harmonic emission level
根据叠加原理有:

用户侧与系统侧谐波电压发射水平分别为
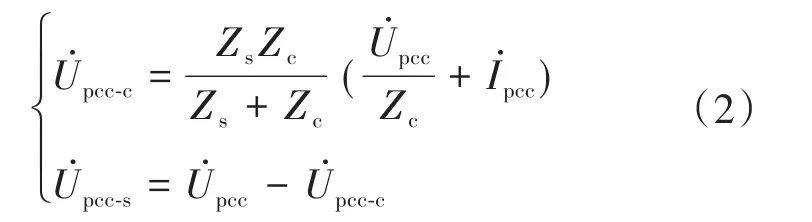
对于传统非线性用户的工况,由于两侧谐波阻抗满足|Zc|>> |Zs|,从而近似有Zs/Zc≈ 0,因此式(2)中可化解为

即只需求解系统侧谐波阻抗Zs即可量化谐波发射水平。但在高电缆化率城市电网中,随着电缆与感性元件之间发生感容耦合,Zs在某些频次下可能增大,导致|Zc|>>|Zs|不再成立,需要同时计算Zs与Zc方可量化谐波发射水平。
为准确计算PCC点两侧谐波阻抗,本文提出一种改进的FastICA算法,具体计算方法见第2节部分。
2 改进FastICA算法
2.1 传统FastICA算法分析
根据中心极限定理,独立随机信号线性组合后高斯性将增强。以此为基础,FastICA算法考虑各源信号间的独立性,通过对观测信号X施加线性变换WTX,求取能使WTX非高斯性最大的W,此时WTX即为分离出的源信号。非高斯性可由峭度、负熵等指标度量,其中负熵因其稳健性应用更广[8]。
本文对基于最大负熵的FastICA算法进行研究,负熵近似计算式为

式中:s与sGauss均具有零均值与单位方差,且sGauss为高斯随机信号;E{.}表示求期望;G{.}为非平方的非线性函数。
由式(4)可知,J(s)越大,信号 s的非高斯性越强。
FastICA算法要求各源信号之间相互独立。这一点可通过提取各谐波源信号的快变分量来实现。快变分量可通过计算各信号的波动量来提取,进而有 Δİs与 Δİc近似独立,且源信号实、虚部的波动量也近似独立[7-8]。将 [ΔU̇pccΔİpcc]T与[ΔİsΔİc]T的实、虚部解耦如下:

式中:ΔUpcc-x,ΔUpcc-y,ΔIpcc-x与ΔIpcc-y分别为ΔU̇pcc与Δİpcc的实、虚部;ΔIc-x,ΔIc-y,ΔIs-x,ΔIs-y分别为Δİs与Δİc的实、虚部。anp(n,p=1,2,3,4)为混合系数,其取值只与两侧谐波阻抗有关。
令 X=[ΔUpcc-xΔUpcc-yΔIpcc-xΔIpcc-y]T,S=[ΔIc-xΔIc-yΔIs-xΔIs-y]T,可由式(5)得到其对应的盲源分离模型矩阵形式如下:

FastICA算法以负熵最大为目标,先对X进行中心化、白化预处理[8-10],再逐行优化解混矩阵W,将源信号从观测信号中逐个分离出来,得到谐波源近似信号 Y=[Yc-xYc-yYs-xYs-y]T,对应于[ΔIc-xΔIc-yΔIs-xΔIs-y]T,但对应顺序未知。从而有X=ÂY,由矩阵变换有:


式中:Zs-x,Zc-x分别为 Zs与Zc的实部。

至此,通过FastICA算法可分别求得Zc与Zs。
当Zc与Zs幅值满足|Zc|>> |Zs|时,FastICA算法可准确计算较小一侧谐波阻抗Zs;但当Zc与Zs幅值较接近时,如在高电缆化率城市电网中某些频次下,则求得两侧谐波阻抗误差均较大。
由于FastICA算法以各分离信号的负熵最大为优化目标,因而可从以下两点讨论其计算误差来源。
1)欠优化。分离所得源信号Y的非高斯性比真实源信号S的非高斯性小,即优化不够彻底,导致计算误差较大。
2)过度优化。理论上,当随机信号个数趋于无穷时中心极限定理才严格成立,但实际中源信号个数通常较少,如本文源信号数为4。少量源信号通过线性组合后,高斯性通常仍会上升,但也不排除下降的可能。FastICA以负熵最大建立目标函数,有时会出现过度优化,即分离所得源信号的负熵值比真实源信号的更大。
本文模型中源信号的维度较大,中心极限定理绝大多数时候成立,因而FastICA误差多数来自欠优化,少数来自过度优化。
为了在高比例直流城市电网下能准确地计算两侧的谐波阻抗,本文针对以上两点,通过稀疏筛选与综合负熵筛选对传统FastICA算法进行改良。
2.2 稀疏分量法
当FastICA算法分离信号误差较大时,真实源信号S与求得源信号Y并非完全吻合,而是在Y附近,但与Y存在一定差异。为此,本文将SCA与FastICA结合,采用“全局-局部-全局”的思路,先由FastICA分离出源信号的全局近似值;再由SCA构造稀疏筛选判据,在分离所得源信号附近局部搜索,找出可能与真实源信号吻合的局部信号;最后重构局部信号对应的全局信号,并采用综合负熵筛选求得谐波阻抗。SCA算法原理如下。
SCA利用信号的稀疏性提取源信号。当源信号S稀疏时,其值在多数时候为零,少数时候非零,可认为混合信号X在各时刻最多由其中一个源信号生成,此时X线性聚类,由聚类直线斜率可求混合矩阵[15-16]。
实际应用中,通常源信号S并非稀疏信号,需通过稀疏字典D将其转换到稀疏域下,得到稀疏化后的源信号S(D-1)T。对式(6),将源信号S的稀疏字典D同时对S以及混合信号X进行变换,有:
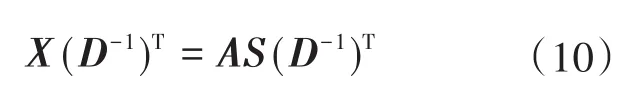
由此可见,该变换不会改变混合矩阵A。
在FastICA分离出的源信号Y附近进行局部搜索,搜索到的局部信号y对应于真实源信号S的3行,以y对应[ΔIc-xΔIc-yΔIs-x]T为例进行介绍。对第i组局部信号yi,通过KSVD算法[17]可根据所需稀疏度(稀疏化后信号非零元素个数)求取其稀疏字典D,并将D作用于对应时刻的混合信号X。由式(10)可知,此时D等同于作用在真实源信号S上。
若yi与对应时刻S吻合,则S也能被稀疏化,对应X(D-1)T仅由一个源信号产生,称该局部采样点为单源点;反之若yi与S不吻合,则对应X(D-1)T由各源信号共同产生,称该局部采样点为多源点[18]。
1)单源点。此时yi与对应时段的S吻合,设定稀疏度为1且信号非零值位于同一时刻,通过yi的稀疏字典D可将 [ΔIc-xΔIc-yΔIs-x]T稀疏化。在yi值为零的采样点,X(D-1)T仅由稀疏变换后的ΔIs-y产生,从而对单源点有
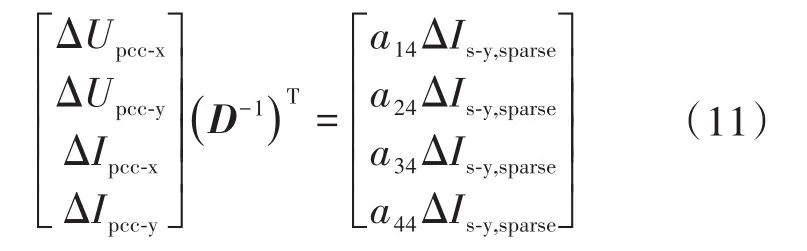
式中:下标“sparse”表示通过D进行稀疏变换后得到的信号。
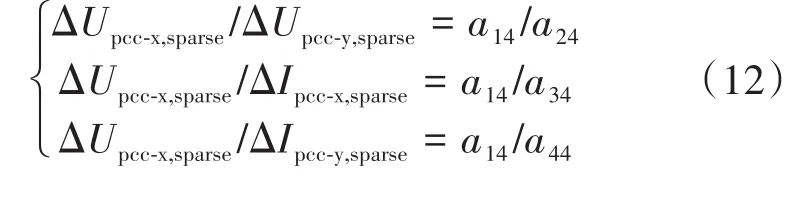
进而可得:可见经过稀疏变换后,X(D-1)T线性聚类,由聚类直线斜率可求得A中某列各元素之间的比例关系。
2)多源点。此时yi与对应时刻S不吻合,通过yi的稀疏字典D无法将S稀疏化,X(D-1)T仍由多个源信号共同产生。仅当下式成立时X(D-1)T才能线性聚类,而大多数局部信号不满足该条件[19]:
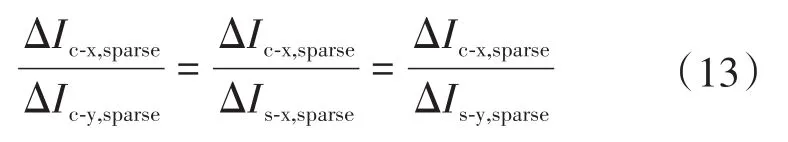
因而可将X(D-1)T线性聚类作为搜索到的第i组局部信号yi与对应时刻真实源信号S吻合的必要条件。由此推导出评估yi与S吻合度的稀疏筛选判据:

式中:Re(.)与Im(.)分别表示取实、虚部;ε为稀疏筛选设定的阈值;j,k=1,2,3,4,且j≠k;m为局部信号yi被稀疏化后,其值为零的采样点位置。
通过聚类直线斜率可求混合矩阵A中某一列中各元素之间相互比例关系。进而结合式(8)、式(9)与式(12)可计算对应侧谐波阻抗。
在FastICA分离出的源信号Y附近进行局部搜索时,若局部信号长度 Llocal<5,则式(14)恒成立,稀疏筛选判据失效,因而要求Llocal≥5。但Llocal较大会增加局部搜索的负担,本文取Llocal=5。此时搜索空间维度为15,通过进一步对信号进行降维变换可将搜索空间维度降至6。将式(14)作为目标函数,上述搜索过程可通过在Y附近进行穷举搜索完成。
2.3 综合负熵筛选
稀疏筛选判据是局部信号yi与对应时刻真实源信号S吻合的必要条件。在大量满足式(14)的局部信号yi中,既存在与S高度吻合的信号,也存在因式(13)而使X(D-1)T误线性聚类的信号。因而需对稀疏筛选后得到的各组局部信号yi进行二次筛选。
从信号的非高斯性入手研究筛选方法。Fast-ICA的误差来自对信号非高斯性的欠优化或过度优化。由于中心极限定理近似成立,实际中以欠优化为主,而过度优化情况较少。即使出现过度优化,往往也只发生在某个源信号上,此时其余源信号仍处于欠优化状态。
当分离所得信号误差较大时,一般存在两种现象:1)分离出的各信号非高斯性均较弱;2)分离出的信号中某信号非高斯性较强,其余信号非高斯性较弱。而对于真实源信号,各信号均具有较强非高斯性。
对某局部信号yi,可由式(8)、式(9)与式(12)计算其对应侧的谐波阻抗,进而由下式重构其对应的全局信号:
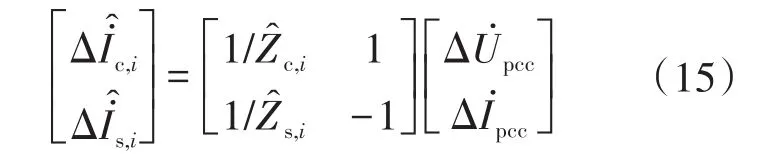


令稀疏筛选后第i组局部信号对应全局信号实虚部的负熵分别为 Jx,i与 Jy,i,通过下式可将 Jx,i归一化为 J'x,i。Jy,i归一化方式同理。
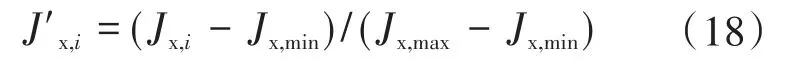
式中:Jx,min,Jx,max分别为稀疏筛选后各组局部信号对应全局信号实部负熵的最小值与最大值。
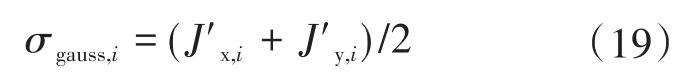
稀疏筛选后,通过综合负熵筛选最终可找到与真实源信号高度吻合的局部信号,并避免欠优化与过度优化。进而可求取谐波阻抗,评估谐波发射水平。
改进FastICA评估谐波发射水平的原理及流程如图2所示。
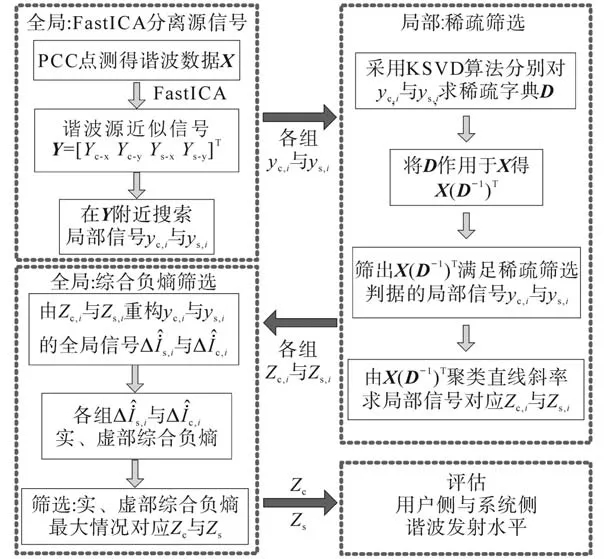
图2 改进FastICA评估谐波发射水平原理示意图Fig.2 Schematic diagram of improved FastICA evaluating harmonic emission level
3 仿真分析
3.1 各算法误差对比
对图1所示诺顿等效电路设置仿真数据,并由式(1)生成PCC点谐波数据。具体仿真参数设置如下:1)谐波电流源:İc幅值为 100 A,相角为-30°。İs幅值为İc的k倍,相角为30°,考虑到城市电网高电力电子化率下,PCC点背景谐波可能较大,本文取 k=0.6,0.8,1.0,1.2,1.4,1.6。İc和 İs的幅值与相角均加上10%的正弦波动与±5%的随机扰动。2)谐波阻抗:考虑城市电网高电缆化率下,电缆与感性元件发生感容耦合可能导致Zs增大且不再远小于Zc,设Zs=5+15j Ω,Zc=8+23j Ω,并对Zs,Zc的实、虚部分别叠加±10%的正弦波动。
按上述设置生成15 000个仿真数据,为保障单次计算中谐波阻抗近似恒定不变,每150个数据为一段进行一次计算。采用4种方法(方法1:二元回归法;方法2:独立随机矢量协方差法;方法3:传统FastICA;方法4:改进FastICA)计算Zs。由于现有方法大多只能计算系统侧谐波阻抗,对用户侧谐波阻抗,仅对比传统FastICA算法与改进FastICA算法。
上述4种方法对应的计算误差如图3所示。由图3可见,即使背景谐波波动很小,方法1、方法2求得Zs的误差仍较大,这是因为他们的基本假设|Zc|>>|Zs|不满足。此外,随着背景谐波的增大,其误差迅速大幅上升,说明这两种方法受背景谐波波动的影响较大。方法3相比于方法1、方法2具有较强的抗背景谐波波动能力,但由于|Zs|与|Zc|较接近,求得谐波阻抗误差仍较大。且随着背景谐波波动增大,Zs误差增大,而随着背景谐波波动减小,Zc误差增大,即更难求准谐波源波动较大侧对应谐波阻抗。
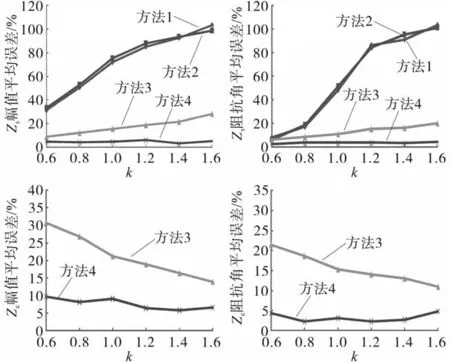
图3 各方法求得Zs与Zc平均误差Fig.3 Average error of Zsand Zccalculated by each method
相比之下,改进FastICA算法通过稀疏筛选找出与真实谐波源信号高度吻合的局部信号,再由综合负熵筛选避免了对负熵的欠优化。求得两侧谐波阻抗的精度高,可进一步用于评估谐波发射水平。
3.2 FastICA误差分析与筛选机制合理性研究
前文分析FastICA算法的误差来自对负熵的欠优化或过度优化,下面对此验证,并分析所提筛选机制的合理性。
以k=1(背景谐波较大)以及k=0.1(背景谐波较小)为例,对于FastICA算法分离所得的信号Y,以及真实源信号S,通过对比他们的负熵分析误差来源。先由式(17)将Y与S化为零均值单位方差的信号。进而令Y与S的负熵分别为J(Y)与J(S),通过计算J(Y)-J(S)可对比两者负熵大小。独立运行FastICA算法200次,对比结果如表1与图4、图5所示。

表1 FastICA误差原因分析(k=1|k=0.1)Tab.1 Analysis for the error of FastICA(k=1|k=0.1)

图4 S与Y负熵对比(k=1)Fig.4 Negative entropy contrast:J(S)vs J(Y)(k=1)

图5 S与Y负熵对比(k=0.1)Fig.5 Negative entropy contrast:J(S)vs J(Y)(k=0.1)
由表1与图4、图5可看出,FastICA分离所得各源信号以欠优化为主,偶尔出现过度优化,且某侧谐波源实、虚部同时被过度优化的概率极低。原因在于,中心极限定理在该模型中近似成立,当计算存在较大误差时,真实源信号的非高斯性通常强于分离所得信号。此外,当k=0.1时,背景谐波很稳定,此时理论上求得Zs精度较高。由图5可见,相比于图4,Ys-x与Ys-y欠优化的频次明显下降,准确优化频次增多。此外由表1可见,相比于k=1的情况,k=0.1时Ys-x与Ys-y同时欠优化概率也有所下降。进而说明寻优过程中对信号实、虚部同时欠优化是导致计算误差的主要原因。
本文将传统FastICA算法改良,对各局部信号及其对应全局信号引入稀疏筛选与综合负熵筛选。一方面,筛出的信号具有较大的综合负熵,可避免欠优化;另一方面,当分离所得信号实、虚部分别出现欠优化与过度优化时,对应综合负熵往往并非最大,且由于中心极限定理近似成立使得信号实、虚部同时被过度优化的概率极低,从而该筛选机制也能避免过度优化。
4 实际工程案例分析
以我国某城市电网中某一工业用户为例进行分析。该城市电网的电缆化率较高,在部分区域甚至高达90%以上。电缆与系统中感性元件发生感容耦合,导致系统侧谐波阻抗在某些频次下增大。此外,该工业用户中装有大量的变频器,用于厂区内马达设备的变频启动与调速。同时也装有大量UPS电源,以保障各设备的正常运行。变频器与UPS电源在工作过程中会产生大量谐波,劣化PCC点电能质量。通过评估该工业用户在PCC点的谐波发射水平,有助于量化其谐波责任,进而指导谐波治理方案的制定。
将该工业用户与电网相连的35 kV母线作为PCC点,采集电压、电流数据,得到各次谐波值。其中5次谐波电压、电流30分钟数据如图6所示。

图6 PCC点测得5次谐波电压电流Fig.6 The 5th harmonic voltages and currents at PCC
将图6测量数据均分为10个时段,每时段长3 min,采用4种算法分别计算系统侧与用户侧5次谐波阻抗,计算结果如图7所示。由图7可见,传统算法求得两侧谐波阻抗在短时间内存在较大的波动,这与实际工程情况并不相符。相比之下,所提改进FastICA算法求得结果较稳定,从而间接说明所提方法计算结果更为可信。此外,由计算结果可看出,求得系统侧谐波阻抗并非远小于用户侧阻抗,这是由于高电缆化率下电缆与感性元件发生感容耦合所致。该工况下,传统方法所需假设不再满足,故计算结果精度低,波动性大。进而,基于求得的阻抗,可计算系统侧与用户侧在PCC处的谐波电压发射水平分别为98.32 V与127.51 V。
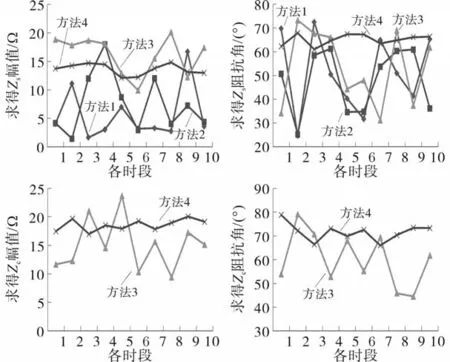
图7 各方法由实测数据求得Zs与ZcFig.7 Zsand Zccalculated by each method according to the measured data
5 结论
本文针对高电缆化率城市电网中非线性用户的谐波发射水平评估进行研究,分析了该问题的难点并提出解决方法,具体结论如下:
1)考虑城市电网高电缆化率以及高电力电子化率,传统谐波发射水平评估方法所需假设不再成立。提出一种改进的FastICA算法。
2)结合中心极限定理,分析了现有FastICA算法计算精度的主要影响因素,论证其计算误差主要来自对负熵的欠优化或过度优化。
3)针对FastICA计算误差来源,引入稀疏筛选与综合负熵筛选机制对算法进行改良。改进FastICA可准确计算高电缆化率城市电网中系统侧与用户侧的谐波阻抗。
此外,在所提算法的局部搜索过程中,如何进一步提高搜索效率是接下来的研究方向。

