基于球形解码算法的逆变器模型预测控制策略研究

徐瑞，潘三博

（上海电机学院电气学院，上海 200000）

逆变器控制方法中研究最多的课题之一就是电流控制。在过去的几十年里，有两种传统控制方法得到了广泛的研究，分别是滞环控制和基于脉冲宽度调制（pulse width modulation，PWM）的线性控制方法。

滞环电流控制的基本思路是每当电流达到边界条件时，可改变逆变器的开关状态来确保电流处于滞环带内部[1]。这种方法在概念上比较简单，但存在谐振问题[2]。对于基于PWM的线性控制，这种控制方案的性能取决于控制器的设计参数和参考电流频率[3]。虽然比例积分（proportional integral，PI）控制器可能确保连续参考信号的稳态误差为0，但存在明显误差。随着参考电流频率增高，误差随之增大。

随着对更高效率功率变换器的追求，近几年模型预测控制（model predictive control，MPC）在电力电子领域取得快速发展。在电力电子领域，最直接有效同时容易应用的预测控制器就是使用单步预测，调节多个变量跟踪其各自的参考值[4]。直接MPC参考跟踪的优化问题跟踪是基于整数决策变量的。这意味着当预测长度延长时，可能的解决方案的数量会成倍增加，难以计算[5-7]。通常认为单步预测可以满足大部分需求，这种观念源于多步预测导致潜在解的组合数量巨大。而逆变器驱动系统多步预测会带来很客观的性能提升。可通过降低开关频率或总需求失真（total demand distortion，TDD），或同时降低两者来提升逆变器的稳态性能[8-10]。

本文提出了一种控制策略，改进多步长MPC由于成倍增加的解决方案的数量造成的计算困难问题，从而实现对逆变器的多步长预测控制，提升逆变器的工作效率及稳定性。

1 设计方案

控制策略在直接模型预测控制的基础上，将控制器模型的优化问题以向量的形式重新构造并将其表示为一个整数二次规划。由于三相逆变器电压电平数量有限，整数搜索空间减小。在初步优化的基础上，本控制方法通过对基于分支定界技术的球形解码算法的改进，进一步缩小解决方案的数量，最终对优化问题进行求解，寻找最佳的切换序列。

1.1 控制器目标

本文以感应电机作为负载的三相逆变器电路示意图如图1所示。

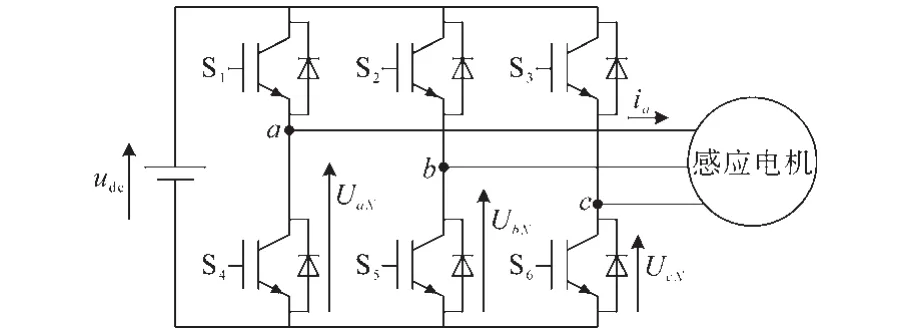
图1 三相逆变器电路示意图Fig.1 The schematic of three-phase inverter circuit

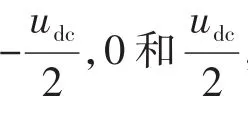
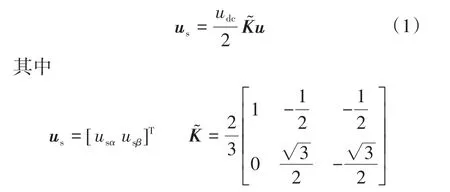
式中：usα,usβ为定子电压在α，β轴的分量。

定子电流isα，isβ和转子磁链Ψrα，Ψrβ作为状态变量。转子的角速度被视为一个（相对缓慢变化的）变量。

电流控制器的目标是通过改变三相逆变器的开关位置调节定子电流，使之随参考值的变化而变化。实现该目标的控制基本原理如图2所示。

图2 控制原理图Fig.2 Control schematic diagram

1.2 控制器模型

对预测模型的推导，可以很方便地引入状态矢量驱动模型，即

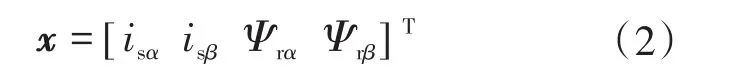
定子电流作为系统输出矢量，即

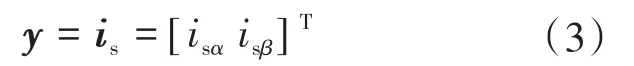
而三相开关位置u构成输入矢量，由控制器提供。通过以上参数，可以得到状态方程：

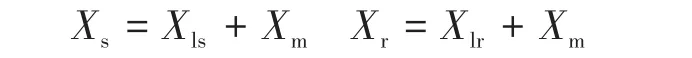
式中：τr，τs分别为转子、定子时间常数；Xls，Xlr，Xm分别为定子、转子和互感电抗。

2 优化问题

2.1 代价函数

一般通过代价函数的最小化，得到合适的开关切换序列。

代价函数J表示如下：

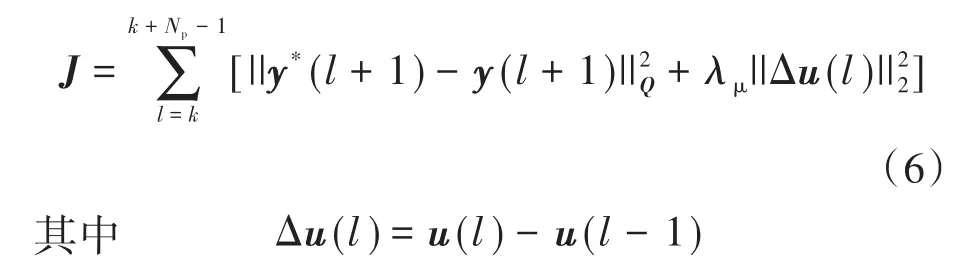
式中：k为时间步长；Np为预测时间步长；λμ为权重系数；Q为参考值与反馈值间产生的误差形成的惩罚矩阵。

式（6）中，第二部分表示对开关变化的限制。开关只能在上一个周期中上升或下降一个单位，因此||Δu(l)≤1，它表示了三相逆变器系统中三相桥臂a，b，c的开关位置。

由式（6）可知，代价函数由输出跟踪误差和系统的开关量两部分组成。前者对应于负载电流的总需量畸变，后者表现为开关频率。一般情况下，为了降低高阶系统中负载电流的脉动，将会增加跟踪误差的权重，而相应的减少逆变器电流和电容电压权重。输出跟踪误差和开关量都包含在代价函数中，两者之间的权衡问题通过对权重系数λμ的改变进行调整。

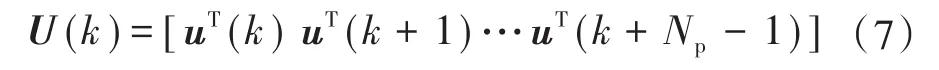
式中：U(k)表示预测控制器所需要决定的三相逆变器的桥臂开关状态位置的顺序。

式（7）代表控制器给出的三相逆变器的开关切换序列。基于参考跟踪的直接MPC的优化问题可以被描述为

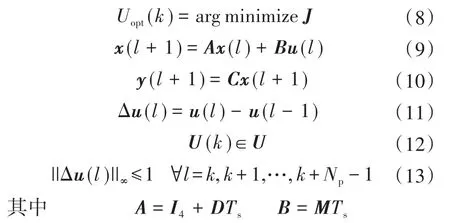
式中：I4为四阶单位矩阵；Ts为周期系数；U为逆变器开关切换序列集合。

2.2 整数二次规划

以向量形式重新构造优化问题（11），并将其表示为一个整数二次规划。由于逆变器电压电平数量有限，整数搜索空间减小。

综上，MPC与跟踪参考值的问题现在可以描述为整数二次规划。最佳的切换序列，通过最小化的代价函数式（23）、约束式（12）和式（13）得到：

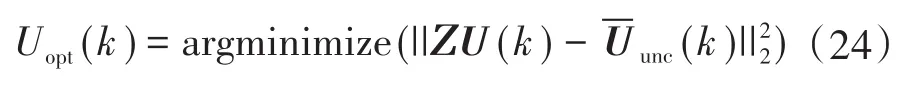
3 球形解码算法求解优化

3.1 改进的球形解码算法

该算法的基本思想是迭代考虑候选序列[11]，即U(k)∈ U，球面半径ρ(k)＞ 0，集中在

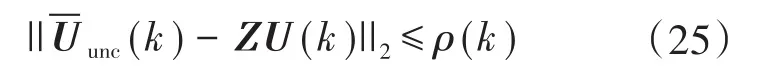
满足开关约束式（13）。

用于球形解码的一个关键特性，由于Z是三角形的，所以识别满足式（25）的候选序列非常简单[12]。由于Z是下三角，式（25）可以改写为

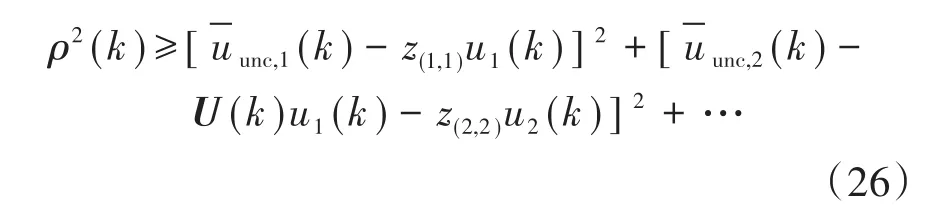
式（25）的解集可以通过以下方式找到：要确定U(k)，该算法需要在时间步长k中使用的半径初始值设为ρ(k)。一方面，半径ρ(k)应尽可能小，使我们能够尽可能多地消除许多候选切换序列。另一方面，ρ(k)不能太小，以确保解决方案集不是空的。应选择初始半径为基础。

切换序列Uini（k）表达式如下所示：

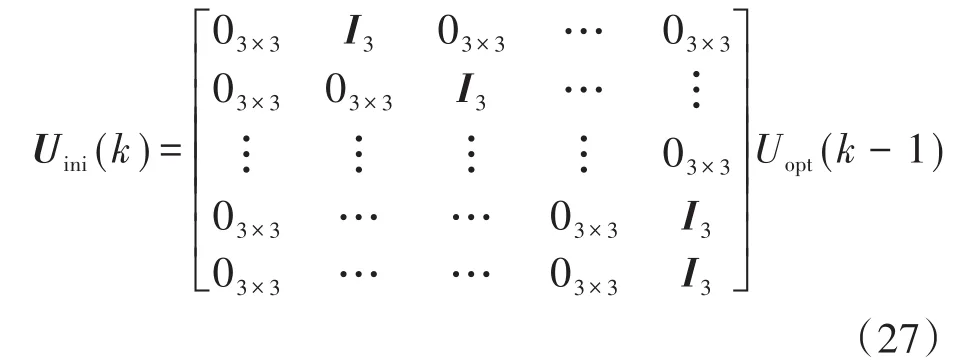
被猜测的切换序列Uini（k）通过将上一周期的最优切换序列向后移动一个周期并以最后的开关状态得到。因此，Uini（k）是满足目标条件的解决方案。

ρ(k)给出的初始值设置为

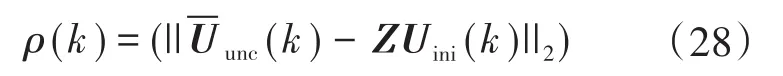
在每一个时间步长k，控制器首先使用当前状态x(k)、参考值Y*(k)、以前的开关位置u(k-1)和以前的Uopt(k-1)，(k)计算Uini（k），ρ(k)，见式（27）和式（28）。

算法的流程图如图3所示，其中v(i,1:i)为U的第i行，1到i列的元素组成的行矩阵；u1:i为u(k)的第1到i行组成的列矩阵。由图3可以看出，从第一个分量开始，通过考虑集合U中允许的单项开关位置，逐个分量的构建开关序列U（k）。如果关联的平方距离小于当前的ρ2(k)值，那么继续下一个分量。一旦到达最后一个分量即U3Np(k)，意味着 U（k）是全维的，那么 U（k）就是候选解。如果U（k）满足切换约束，并且距离小于当前最优值，则更新现有最优解Uopt(k)和半径ρ(k)。

图3 球形解码算法流程图Fig.3 Flow chart of spherical decoding algorithm

3.2 改进球形解码算法中搜索树的遍历

令预测步长Np=2，分析该算法的工作过程。该算法的优化问题是找到可能的逆变器开关切换序列U中的集合长度为3Np的最优切换序列Uopt(k)。

集合U是跨越深度为3Np的树，每个节点后连接了三个子节点。等级i上的节点对应于关于U中的第i个元素进行的切换决策。具体来说，从级别i的结点开始的分支与ui有关。依次访问从根节点到树叶之一的树对应于唯一的开关切换序列。

当设置的预测步长为Np=2的情况下，在图4中展示了搜索树的搜索过程。从i=1处的根节点开始，算法评估u1∈U。选择u1=-1超过球体的半径，并且对u1=-1开始的子树进行修剪。u1=0的选择在球体内部，从该位置继续向下一树枝进行搜索，算法进行到级别2，而并不去对u1=1的分支进行探索，即将该分支修剪舍弃。算法的探索方向在途中用箭头表示。

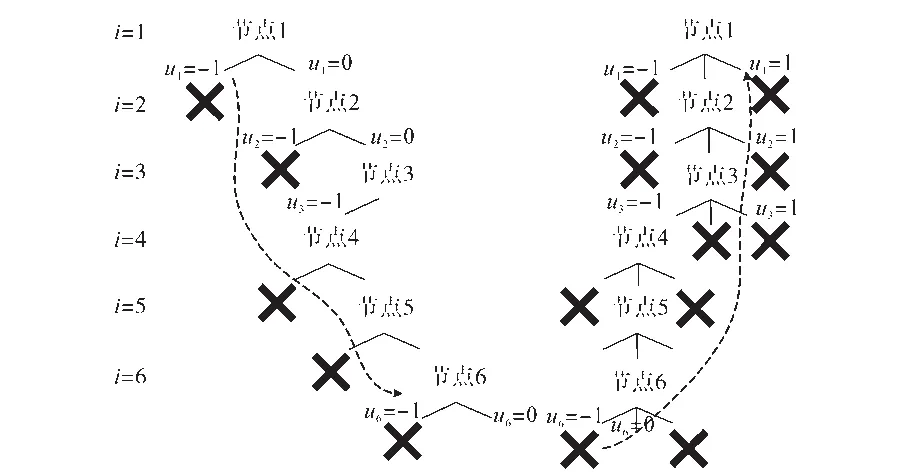
图4 预测范围为2的球形解码算法对搜索树遍历可视化Fig.4 The sphere decoding algorithm with a prediction range of 2 visualizes the search tree traversal

在对六个节点进行依次探索之后，得到了第一个可用的逆变器开关候选序列U=[0 0-1 0 0 0]T，该开关位置的候选序列来自于试探性的开关位置u（k）=[0 0-1]T和u（k+1）=[0 0 0]T。该候选序列中对应的元素所对应的叶子节点用圆形表示。如图4右半部分所示，在进行下一次的节点搜索之前，球体的半径已经被减小，球体缩进。再到目前为止访问的节点上搜索剩余节点所代表的开关切换序列，同时，在搜索树中沿着树枝的方向朝着树的根节点继续探索。由于算法的严格球面搜索和深度的搜索过程，在探索最小节点数之后的大部分情况下，找到了最优的切换序列。

3.3 搜索树中探索节点数量分析

在多个不同的基本周期中，记录算法在每个时间周期中需要调查的节点数量。表1为以平均和最大的节点数作为预测范围的函数。

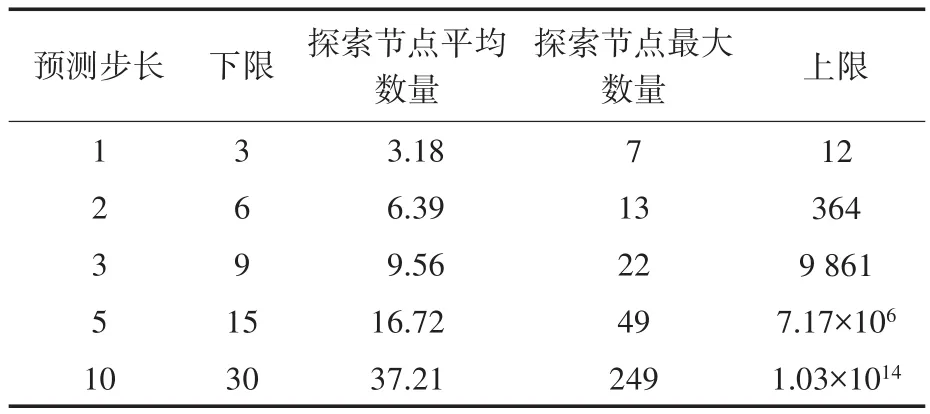
表1 在搜索树中探索的节点数量Tab.1 The number of nodes explored in the search tree

图5为在预测步长为10时，每个周期中改进算法在工作过程中所需要探测的平均节点数的统计图。由图5可知，直方图的高度绝大多数分布在概率30%以下。对于本算法，在80%的情况下，对于寻找最佳切换序列的优化问题可以通过只对一个候选序列进行搜索来解决。

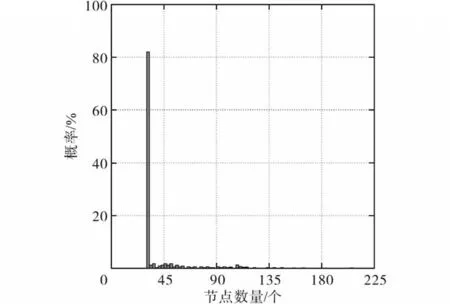
图5 节点数目分布图Fig.5 The distribution diagram of the number of nodes

4 仿真与实验

4.1 权重系数的选择

为了说明权重系数λμ对系统稳态性能的影响，将控制策略的预测步长固定为5，改变权重系数的值，得到相应的谐波失真情况及开关频率变化情况如图6、图7所示，对应λμ的增加，代价函数中开关频率所占的权重增加，从而降低开关频率，但相应的，总谐波失真和跟踪误差会增大。从图6、图7中可以看出，当10-2≤λμ≤1时，改变λμ值可以起到平衡开关损耗和系统稳态性能的作用。因此，权衡两种因素，最终选取λμ=0.15。

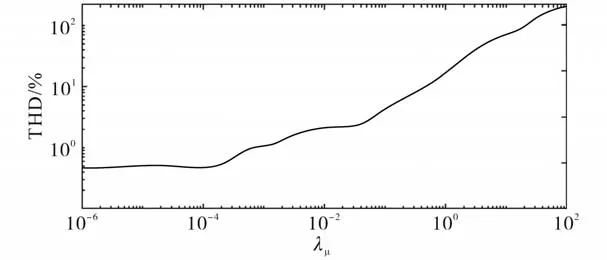
图6 总谐波失真随权重系数的变化Fig.6 Change of total harmonic distortion with weight coefficient

4.2 基于改进球形解码算法模型预测控制的逆变器系统仿真

为了验证上述理论分析的合理性与可行性，在Matlab/Simulink上进行仿真验证。主要仿真参数如下所示：直流电源电压U=715 V，参考电流幅值I=280 A，参考电流频率100π rad/s，求解器类型为固定步长，求解器为ode5，固定步长范围1e-6，采样周期Ts=25e-6 s。

为了证明多步长预测带来的优越性能，设预测步长N=4并保持不变。仿真实验结果如图8、图9所示。

图8 交流侧三相电流Fig.8 Three-phase currents on the AC side

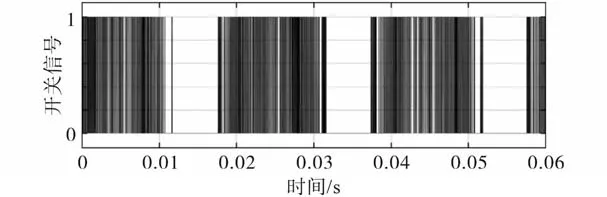
图9 开关状态Fig.9 Switch status

交流测单相电流如图8所示。可以看出电流波形平滑，而电流的跟踪精度较高。

图9为开关状态，可以看出不存在重复的开关模式，因此电流谐波在不同次数下都比较平坦。

4.3 仿真结果及分析

图10为N=1时传统模型预测控制下的逆变器系统负载电流的FFT分析结果，THD为5.20%。图11为N=4时改进球形解码算法模型预测控制下逆变器系统负载电流的FFT分析结果，THD为2.34%，较传统模型预测控制减小2.86%，降低了电流的畸变程度。

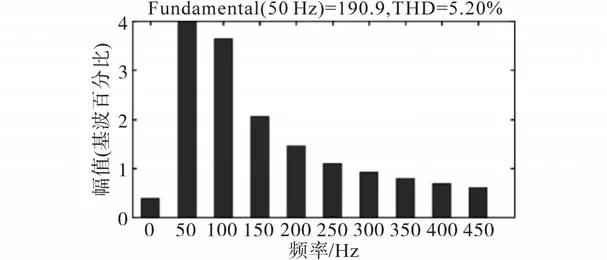
图10 传统模型预测控制负载电流频谱分析Fig.10 Load current spectrum analysis of traditional model predictive control

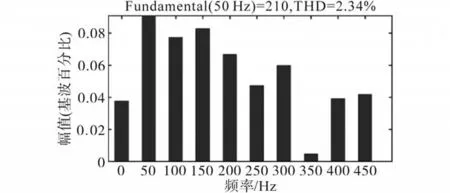
图11 改进模型预测控制负载电流频谱分析Fig.11 Load current spectrum analysis of improved model predictive control

新型控制系统的Bode图如图12所示，在0～400 Hz之间曲线拟合度精度很高，因此在中低频阶段会有较好的零相移、单位增益特性，而在高频段，幅值补偿快速下降到-28 dB以下维持系统稳定。证明了球形解码算法的稳定性，能够实现对电流参考值的准确跟踪，实现逆变的效果。

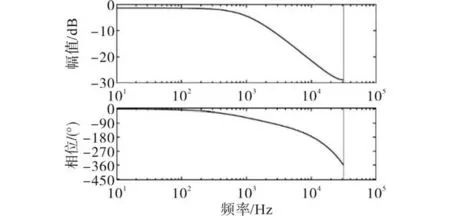
图12 系统Bode图Fig.12 Bode diagram of the system

基于球形解码算法的多步长模型预测控制与传统模型预测控制在不同预测步长下的计算时间比较如图13所示。随着预测步长的增加，基于球形解码算法的模型预测控制的计算优势越发明显，计算时间远远低于传统模型预测控制。

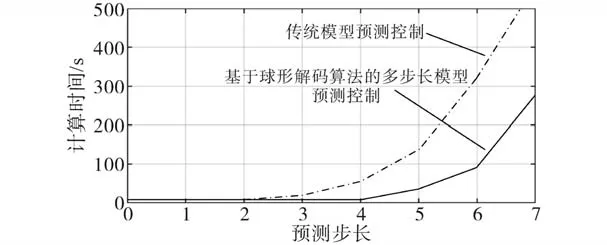
图13 2种控制方法在不同预测步长中的计算时间比较Fig.13 Comparison of calculation time with two kind of control method in different prediction steps

因此该算法应用于MPC中，带来计算优势的同时并不以牺牲最优为代价。该控制策略在极大地降低计算量的同时依旧拥有直接MPC的精确跟踪参考值，有效解决谐振问题等优点。

4.4 实验结果及分析

在上述仿真的基础上搭建逆变器系统平台进行实验，给定放电功率165 kW，示波器测量实际功率：168.7 kW，实验结果如图14、图15所示。

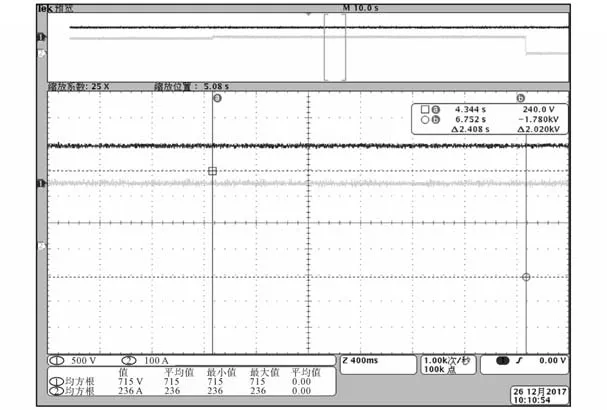
图14 直流侧电流电压Fig.14 DC side current and voltage

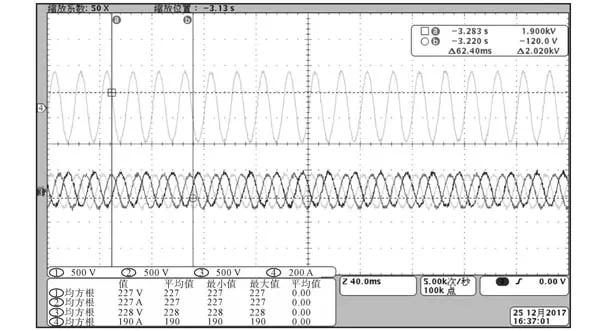
图15 交流侧单相电流和三相电压Fig.15 Single-phase current and three-phase voltage on the AC side

直流侧电压电流如图14所示，直流侧电压715 V，直流侧电流236 A。交流侧电流、电压如图15所示。交流侧三相电压227 V，A相电流有效值190 A，交流侧电压、电流呈现良好的正弦波形，达到预期效果。

5 结论

本文提出了一种基于改进球形解码算法的逆变器MPC控制策略。该策略在直接模型预测控制的基础上，通过基于分支定界技术的改进球形解码算法，缩小解决方案的数量，最终对优化问题进行求解，寻找最佳切换序列，实现对逆变器控制。

1）本文采用整数二次规划对三相逆变器系统进行建模，将球形解码算法应用到模型中，缩小开关序列集合，在得到最优切换序列过程中缩短计算时间，减小计算复杂度。

2）本文提出的改进球形解码算法模型预测控制与传统模型预测控制相比可以将THD降低2.86%，降低电流畸变率，提升逆变器的稳态性能和工作效率。