感应电机无权重分配有限集模型预测控制设计

顾明 ，邢勐，葛贤军

（1.中国石油化工股份有限公司广州分公司，广东 广州 510725；2.中国石油化工股份有限公司炼油事业部，北京 100728；3.电力系统及发电设备控制和仿真国家重点实验室（清华大学电机系），北京 100084）

感应电机驱动控制一直是电力传动领域最为经典和应用价值最广泛的研究内容之一[1-2]。随着新能源汽车产业的爆炸式发展，电机驱动系统的控制策略更是引起了学术界和工业界广泛的关注[3-4]。

目前感应电机控制的方案主要有磁场定向控制方案和直接转矩控制（direct torque control，DTC）方案。前者于1972年首次提出[5-6]，而DTC则是于稍晚的1986年发明[7]，但当时都没有现代化的微处理器芯片。此后随着微处理器的发展，磁场定向控制和DTC技术都得到了一些改进和发展[8-9]，性能虽逐步提升，但理论上无重大变化。随着微处理器实时计算能力从量变到质变，各种新颖的计算密集型算法得以在电机驱动控制中应用，其中最具有代表性的就是有限集模型预测控制[10-14]，其已用于感应电机[12]、永磁同步电机[13]和开关磁阻电机[14]等。有限集模型预测控制中的控制集合即电力电子装置的开关状态组合，由于有效开关状态组合是有限的，故数学上属于有限集。基于有限集和预测模型可进行成本函数评估，从而选择最优开关状态输出，其中成本函数则是根据系统约束和控制目标设计，故有限集模型预测控制可处理系统非线性和多个控制目标，且其计算密集，故具有动态响应极快的优势。

目前，绝大多数文献中用于感应电机转矩和磁链控制的有限集模型预测控制器均使用了含多个权重系数的单个成本函数设计[15-17]。而权重系数的选择则是一个难度较大的问题，通常是由反复试验实际测试得到的，这将耗费大量时间，在工程上也难以实践[18-20]。

本文提出了一种用于感应电机驱动系统的无权重分配优化有限集模型预测控制方案，可实现预测转矩和磁链控制。新方案是一种顺序模型预测控制，不使用权重系数，而是对系统中的每个控制目标使用单个成本函数的顺序结构，其中第一顺序为转矩控制，第二顺序为磁链控制。这便以一种非常简单的逻辑解决了与权重系数设置有关的所有问题。最后，实验结果验证了所设计的优化有限集模型预测控制器的性能。

1 感应电机驱动系统数学模型

1.1 逆变器数学模型

使用三相两电平逆变器的常规感应电机驱动系统电路见图1，逆变器每相桥臂两个功率开关器件以互补方式工作，采用开关函数Sa，Sb和Sc描述，其中上管导通为“1”，反之为“0”。

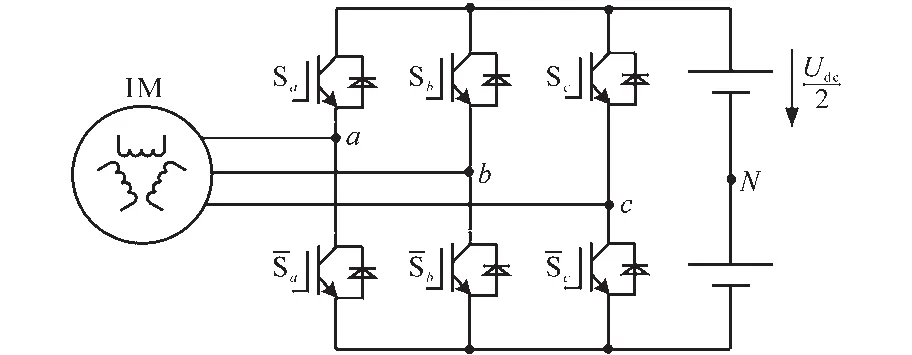
图1 逆变器电路拓扑Fig.1 Circuit topology of the inverter

图2给出了空间矢量图，图中包含有8个电压矢量，分别为u0，u1，u2，u3，u4，u5，u6和u7，其中u0和u7为零矢量。电压矢量和开关状态之间的对应关系见表1。

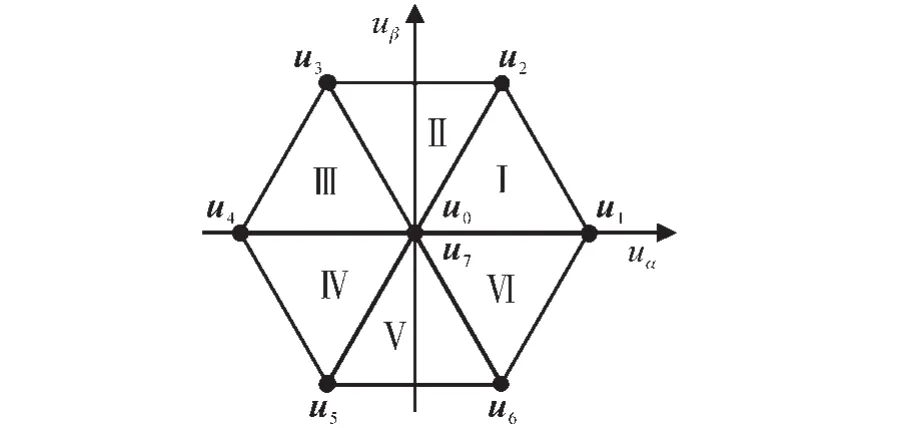
图2 空间矢量图Fig.2 Diagram of the space vectors

表1 电压矢量和开关状态之间的对应关系Tab.1 Correspondence between voltage vectors and switching states

描述三相两电平逆变器的数学模型为

式中：ua，ub，uc为逆变器三相输出电压；Udc为直流电压；uα，uβ为逆变器输出电压α，β轴分量。

1.2 感应电机数学模型

将定子磁链和电流作为状态变量，可得到感应电机数学模型为

式中：us为定子电压矢量；is，ir，Ψs，Ψr分别为定、转子电流和磁链矢量；Rs，Ls，Rr，Lr分别为定、转子电阻和电感；Lm为励磁电感；ω为转子转速；T，TL分别为电磁转矩和负载转矩；J为转动惯量；p为极对数。

2 预测模型

首先在第k个采样周期估计定子磁链Ψs和转子磁链Ψr，Ψr可计算如下：

式中：τr为转子时间常数。

设采样周期为Ts，使用反向欧拉离散化，估计转子磁链的离散时间域方程为

式中：下标“k”和“k-1”分别代表第k个和第k-1个采样周期。

推导得定子磁链估计方程为

通过正向欧拉离散化可得定子磁链预测方程为

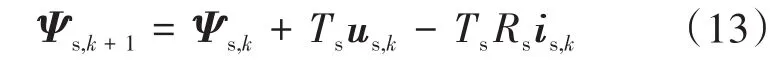
定子电流预测也可通过正向欧拉离散化获得：

3 感应电机优化有限集模型预测控制设计

3.1 无权重分配优化有限集模型预测控制设计

感应电机驱动系统的优化有限集模型预测控制器采用顺序级联预测控制形式，即应用一簇成本函数来实现多个控制目标，当每个控制目标都具有单独的成本函数时，就规避了传统包含权重系数设置的成本函数的使用，从而无复杂的权重系数整定过程。

值得注意的是，在有限集模型预测控制器实现中，由于采样、数字处理和算法执行都需要时间，即非瞬时，故必须考虑最优矢量应用的延迟。为了补偿该延迟，采用两步预测法[21]，即将预测延伸至第k+2个预测控制变量以补偿数字延迟。图3为新型无权重分配优化有限集模型预测控制器框图。

图3 新型无权重分配优化有限集模型预测控制器框图Fig.3 Block diagram of novel optimal finite set model predictive controller without weight distribution

如图3中所示，首先将参考转速ω*和测量转速ω间的误差送入PI调节器以输出参考电磁转矩T*，见标注①。转矩控制的成本函数g1由下式给出：

式中：Tk+2为第k+2个采样周期的预测电磁转矩。

成本函数g1在图3框图中用②标注，计算中将代入逆变器7个有效电压矢量进行计算和评估，而输出使g1最小（即具有最小转矩误差）的2个电压矢量给到磁链控制成本函数g2。评估g2可得使磁链误差最小的最优矢量，g2为

式中：Ψs，k+2为第k+2个采样周期的预测磁链。

将前一步骤中得到的2个电压矢量代入式（18）进行计算和评估可得最终输出最优矢量，见图3框图中标注③。此外，图3框图中标注④代表逆变器输出最优电压矢量；标注⑤代表式（11）和式（12）的磁链估计；标注⑥代表式（17）和式（19）的转矩和磁链预测。

图4为新型无权重分配优化有限集模型预测控制的算法流程图。其中主要步骤如下：1）在步长k测量定子电流is和转速ω；2）在系统中应用上一步长k-1得到的最优矢量；3）在步长k估计定子和转子磁链；4）将7个有效矢量代入g1计算；5）选择使g1最小的2个矢量；6）将选出的2个矢量代入g2最小计算得到最优矢量。

图4 新型无权重分配优化有限集模型预测控制流程图Fig.4 Flowchart of novel optimal finite set model predictive control without weight distribution

3.2 无权重分配优化有限集模型预测控制设计

图5a和图5 b分别为传统DTC方案和传统有限集模型预测控制方案的框图。

图5 传统DTC方案和有限集模型预测控制方案框图Fig.5 Block diagram of traditional DTC and finite set model predictive control schemes

对比图4和图5可总结出优化后的新有限集模型预测控制方案较之传统DTC方案和传统有限集模型预测控制方案的优势如表2所示。

表2 三种方案对比汇总表Tab.2 Comparison summary table of the three schemes

4 实验验证

为验证所设计的应用于感应电机驱动系统的无权重分配优化有限集模型预测控制策略，利用对轴安装的两台2.2 kW鼠笼式感应电机为主体搭建了图6所示的实验平台，开展了测试。其中负载电机由3 kW丹佛斯逆变器（VLT FC302）驱动，而测试主电机由14 kW科尔摩根（SERVOSTAR620）逆变器驱动，改进该逆变器后可实现三相IGBT独立控制，控制器由dSPACE实时仿真系统实现，转速由增量编码器测量。

图6 实验平台Fig.6 Experimental platform

其他实验系统主要参数如下：采样频率fs=16 kHz，直流电压Udc=582 V，感应电机定子电阻Rs=2.68 Ω，感应电机转子电阻Rr=2.13 Ω，感应电机励磁电感Lm=275.1 mH，感应电机额定转速ωnom=2 772 r/min，感应电机额定转矩Tnom=7.5 N·m，感应电机额定电压Unom=380 V，感应电机定子电阻Ls=283.4 mH，感应电机转子电阻Lr=283.4 mH，感应电机极对数p=1，感应电机转动惯量J=0.005 kg/m2。

由于新型无权重系数有限集模型预测控制器已规避权重系数设置，故控制器参数主要是采样频率和模型参数，其中采样频率为16 kHz，而控制器中感应电机模型参数和实际电机参数保持一致，见上述参数设置。

图7为在新型有限集模型预测控制器作用下的感应电机驱动系统在正、反转测试下的动态响应测试结果波形图。图8为感应电机驱动系统稳态实验波形图。

图7 感应电机正、反转测试结果Fig.7 Test results of the induction motor forward and reverse rotation

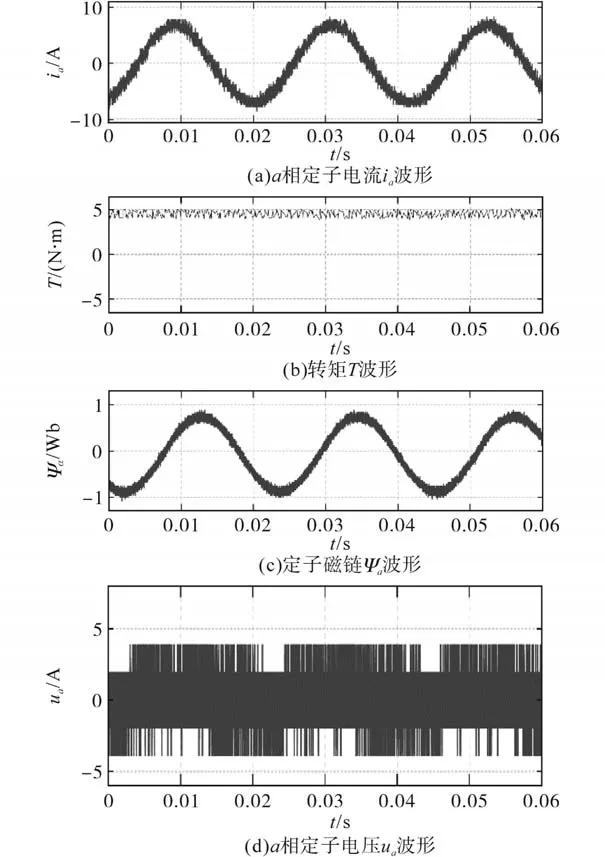
图8 稳态测试结果Fig.8 Test results of the steady state

图7a～图7c分别为转速ω、转矩T和a相定子电流ia的波形，测试结果显示动态过程定子电流幅值快速增加，从而产生了转矩快速变化，转速则从正转2 772 r/min（额定转速）平稳过渡到反转-2 772 r/min。

图8a～图8d分别为定子电流ia、转矩T、定子磁链Ψα和定子电压ua波形，其中ua波形显示在有限集模型预测控制器作用下，呈现出不同于传统PWM调制的电压波形。

图9a为转矩参考和实测值细节波形，图9b为对应定子电流iα波形，结果显示转矩动态响应非常快，其上升时间小于1 ms，且无超调，转矩参考跟踪性能非常好，这是有限集模型预测控制器固有的优点。

图9 转矩动态细节波形Fig.9 Detail waves of the torque dynamic

5 结论

就感应电机驱动系统应用有限集模型预测控制器时的优化设计问题，本文提出了一种无权重分配的简便有限集模型预测控制方案。

经由感应电机驱动系统预测模型推导和实际实验测试可总结结论为：

1）新型有限集模型预测控制方案为每个控制目标赋一个独立的成本函数，并采用顺序级联预测方式进行输出控制，可避免权重系数难以整定的问题，从而降低了控制器设计难度，便于工程实现；

2）实验结果证实了新方案可对感应电机转矩和磁链有效控制；

3）新型有限集模型预测控制方案在概念上不同于传统交流电机既有控制策略，其以简单的方式利用了现代微处理器的高运算能力以及实现了与控制对象（即电机和逆变器）的离散时间域模型的内在关联。

进一步的研究方向是考虑新型控制方案的无速度传感器的实现。