电磁直线执行器控制参数多目标优化设计
黎德祥,陆佳瑜,葛文庆,李波,谭草
(山东理工大学交通与车辆工程学院,山东 淄博 255049)
随着伺服技术的高速发展[1],传统带减速机构的伺服系统因传动结构复杂等原因很难满足越来越高的性能要求,而直驱伺服系统在这方面具有明显优势,近年来在军事、航空航天、汽车及现代机床等领域得到了较快的发展[2-3]。然而,现代工业过程的日益复杂,对控制要求也逐渐提高(如准确性、稳定性、快速性等)[4-5]。
从控制算法的角度看,传统的PID控制、解耦控制和极点配置等方法以及现代控制算法如自适应控制、鲁棒控制、预见控制和滑模变结构控制等方法都在执行器控制领域中不断地得到应用[6-10],但是其控制参数通常是依据专家经验,经过反复试凑和修正才能最终确定和匹配系统的控制参数,导致产品的研制周期长,研制成本高[11]。近年来,粒子群算法[12](particle swarm algorithm,PSA)、遗传算法[13](genetic algorithm,GA)、蚁群算法[14](ant algorithm,AA)等智能优化算法被用于控制参数优化设计,并取得了良好的效果。但是,由于伺服系统的稳定性、信号跟随特性和调节时间等控制目标存在相互排斥及制约的关系,即便采用成熟的单目标优化算法进行优化,往往也很难得到理想的解决方案[15]。因此,国内外一些专家学者对于使用多目标优化方法优化调整控制参数进行了一定的探索和尝试[16]。然而,尽管人们对优化控制器中控制参数做了大量研究,但传统的设计中大多数在优化过程中针对控制器工作时的特性只考虑单个响应特性,并没有在线反馈各种运动状态对控制器的影响,不能实现对控制器控制参数的全面优化设计,并不能从根本上提高其性能要求;同时,对于多目标问题,大多数在求解出Pareto集后,开始人工筛选“最佳值”而没有考虑控制参数对控制系统性能的影响,这会导致主观因素较大,与最佳取值之间存在一定的误差。
本文基于鲁棒控制建立了电磁直线执行器的控制模型,以电磁直线执行器系统误差积分准则(integral of time-multiplied absolute value of error,ITAE)、正弦信号跟踪下的相移量、阶跃信号下的超调量作为优化目标,采用一种高斯自惩罚法与非线性动态惯性权重系数相结合的多目标粒子群优化(multi-objective particle swarm optimization,MOPSO)方法,求解Pareto前沿,最后结合控制参数对控制系统性能的影响选择最终控制参数最优解,并通过试验对控制模型进行了验证。本分析方法可应用于其他伺服系统控制器的控制参数设计优化研究中,提高控制参数调节的效率,节约研发成本,具有一定的工程应用价值。
1 电磁直线执行器结构与模型
1.1 结构与数学模型
本文采用的研究对象为一种高功率密度电磁直线执行器,为上下对称的圆筒形结构,由外磁轭、内磁轭、永磁体、线圈和线圈骨架等部件组成[4],如图1所示。执行器采用Halbach永磁阵列提高驱动能力,相邻线圈电流方向相反以减小电枢反应,具有功率密度高、响应迅速等优势。

图1 电磁直线执行器结构示意图Fig.1 Structure schematic of electromagnetic linear actuator
电磁直线执行器是一个机械、电路和磁路的多场耦合系统[17],电路子系统、磁路子系统以及机械子系统构成的方程组如下:

式中:U为电源电压;ke为反电动势系数;v为线圈运动速度;R为线圈电阻;i为线圈电流;L为线圈电感;km为电磁力系数;M为运动部件的质量;x为运动部件的位移;Ff为摩擦力;Fe为电磁力。
文献[18]给出了一种LuGre动态摩擦力模型,其数学表达式如下:
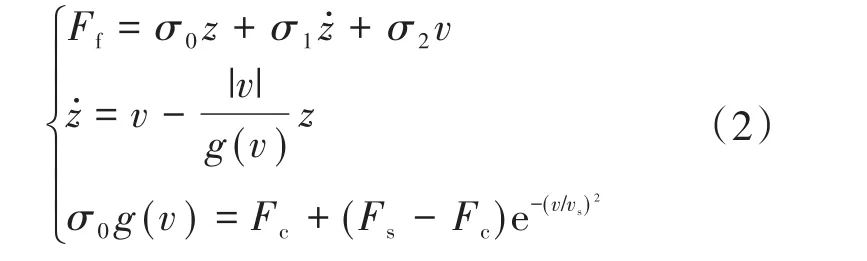
式中:σ0为刚度系数;σ1为微观阻尼系数;z为接触表面刚毛平均变形量;σ2为粘滞摩擦系数;vs为Stibeck速度;g(v)为正定函数,用来描述Stibeck现象;Fc为库伦摩擦力;Fs为静摩擦力。
由于电磁直线执行器电感很小,为简化模型可忽略不计,把式(1)、式(2)结合起来,可得到整个控制系统的状态空间方程组:

式中:u为电压;x1为运动部件的位移;x2为运动部件的速度。
1.2 鲁棒控制系统设计
鲁棒控制器包含线性增益和鲁棒反馈项两部分,其控制系统框图如图2所示。
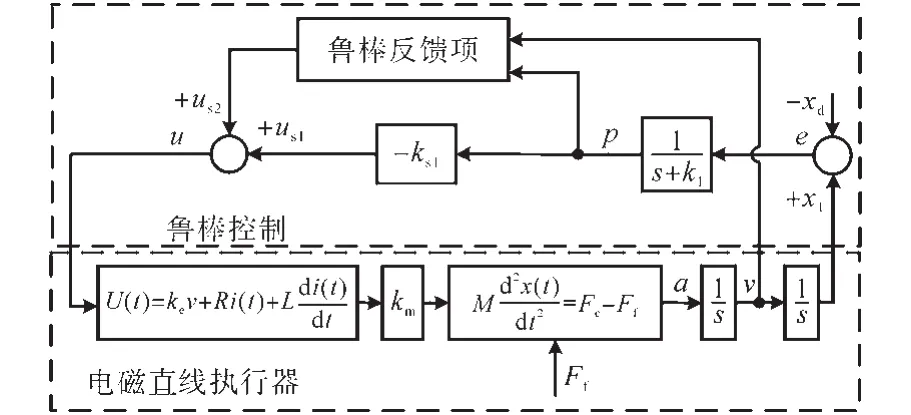
图2 鲁棒控制系统框图Fig.2 The block diagram of robust control system
定义电磁直线执行器的一个类滑模变量p和输出跟踪误差e=x1-xd。其中xd为电磁直线执行器的参考位移,并且有:

式中:us1为比例反馈项;ks1为线性增益;ε0为任意小的常数;us2为用来减弱模型不确定影响的鲁棒项;ks2为一足够大的非线性增益;h0,h1为满足以下条件的任意光滑边界函数:

式中:||||2为欧几里得数。
2 控制参数多目标优化
2.1 设计目标函数
本文对鲁棒控制器的控制参数进行优化。一方面要求控制器以最小代价的损失实现控制目的,以提高控制器的准确性;另一方面要求控制器对电磁直线执行器具有反应迅速和实时跟踪,以提高控制器的快速性;同时要求系统在固有饱和特性的作用下稳定,以提高控制器的稳定性。综合考虑上升时间和误差等约束条件,本文的设计目标维数n=3,选取设计目标函数如下:
1)ITAE准则。用JITAE表示时间与误差绝对值乘积的积分,它反映控制系统在转换状态时,以最小代价的损失实现控制目的,具体表达式为[21]
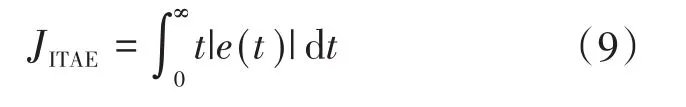
式中:t为时间;e(t)为位移的误差。
2)相移量最小化。正弦信号跟踪下系统的相移反映系统输出跟随输入的特性,相移小,则系统响应就快。所以,通常采用相移量来衡量系统响应的实时性和快速性,具体表达式为[22]

式中:S为相移量;Ncom为FFT序列中输入信号频率分量的下标;fin为控制输入信号的频率;fsam为控制系统周期;N为采样时间;x(t)为控制输入信号;y(t)为控制输出信号;按周期采样后,x(t)信号变为 xn,y(t)信号变为 yn。
3)超调量最小化。阶跃信号下系统的超调量反映了系统输出信号的特性,超调小,输出信号的峰值就小,系统就越稳定。超调量σ具体表达式为

为满足控制器达到最佳的性能,在优化过程以“小JITAE,小S,小σ”为原则进行优化算法中粒子的取舍。
2.2 设计变量及约束条件
根据电磁直线执行器鲁棒控制系统的性能指标要求以及调节经验,选择控制器参数作为优化变量以及约束条件如下。
设计变量为

如上所述,本文设计变量维数m=3,约束条件为

2.3 多目标粒子群优化算法
在传统的粒子群算法(PSO)中,粒子的位置和速度按照下面的公式更新[23-24],即

式中:Vid(n)为第n个粒子的当前速度;ω为惯性系数,一般取值ω∈[0.4,1.0];c1,c2为学习因子,一般取c1,c2∈[0,2];r1,r2为 2个随机数,一般取r1,r2∈[0,1];Pid(n)为粒子本身目前搜索到的最佳位置;Gid(n)为整个粒子群目前搜索到的最佳位置;Xid(n)为粒子的当前位置。
PSO算法有着良好的多峰全局寻优能力,被广泛应用在多目标优化中,但是PSO算法有着收敛速度不足和搜索精度低的缺点。为提高整体算法的全局搜索能力和局部改良能力,本文采用一种基于高斯惩罚函数的多目标随机粒子群优化算法。采用高斯罚函数法对不满足约束条件的点给予惩罚,使目标函数值保持在可行域内;同时利用非线性动态惯性权重系数公式调整粒子的动态惯性权重。
算法中,高斯罚函数及引入罚函数后无功优化目标函数的数学模型表达式为[25]
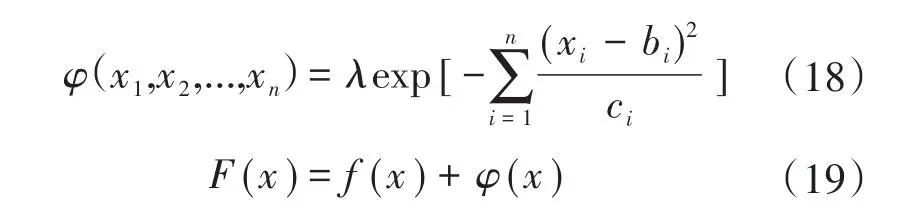
式中:φ(·)为高斯罚函数;F(·)为无功优化目标函数;f(·)为F(·)的初始状态;xi为第i个离散变量;λ为惩罚因子;bi为领域中心;ci为领域因子。由式(18)可知函数值随着矢量 x=(x1,x2,...,xn)T离中心 b=(b1,b2,...,bn)T的距离增加迅速下降为零。在x=b的一个邻域内,F(x)的函数性质与f(x)相差较大,而在离x=b较远的区域,F(x)与f(x)基本重合。
非线性动态惯性权重系数公式为[26]
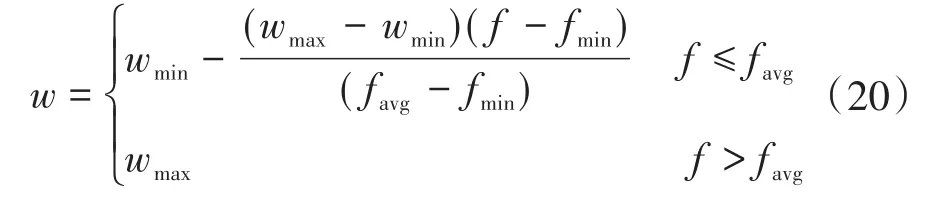
式中:f为当前粒子适应值;favg为当前所有粒子的平均适应值;fmin为当前所有粒子最小适应值;wmax为粒子群最大权重值;wmin为粒子群最小权重值。
本文基于高斯自惩罚法与非线性动态惯性权重系数相结合的MOPSO优化方法具体的优化步骤如图3所示。

图3 基于粒子群算法的多目标优化流程图Fig.3 Flow chart of multi-objective optimization algorithm based on particle swarm optimization
2.4 优化结果
2.4.1 目标函数
采用多目标粒子群优化算法对目标函数进行多目标寻优,经过29次优化迭代,得出可行优化解集如图4所示,其中,实心点为系统推荐的Parteo最优解,空心点为可行解。

图4 多目标优化解集Fig.4 Multi-objective optimization solution set
从图4可知,优化设计中系统ITAE准则、正弦信号跟踪下的相移量、阶跃信号下的超调量存在相互排斥及制约的关系,不能同时达到最优,所以需要根据实际和设计需求选择合适的优化解。
2.4.2 控制参数影响分析
图5为控制参数与控制系统性能的相关系数矩阵示意图。
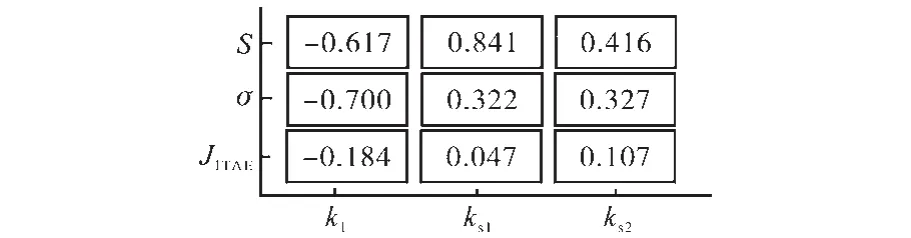
图5 控制参数与控制系统性能的相关系数矩阵示意图Fig.5 Schematic of correlation coefficient matrix between control parameters and control system performance
从图5可知,S与ks1正相关度最大,ks1对σ也有明显影响;σ与ks2的正相关度最大,ks2对S也有明显影响;S与k1负相关度最大,σ与k1的负相关度最大;JITAE与ks2的正相关度最大,与k1的负相关度最大。k1,ks1,ks2对 σ,JITAE和 S 均有一定影响。k1,ks1,ks2为鲁棒控制中的三个关键控制参数,这与实际控制规律吻合。
通过以上对控制参数进行优化,求解Pareto前沿,最后结合控制参数对控制系统性能的影响选择最终控制参数最优解,最终选择控制器主要参数为:k1为 974.5,ks1为 14 280 000,ks2为4 956 000。
3 试验验证与分析
3.1 试验设备
为验证提出算法对电磁直线执行器的有效性,搭建了如图6所示的试验平台,通过基于DSP2812的控制器实现控制算法,控制器集成了电流传感器与H桥驱动模块,执行器的位移由激光位移传感器实时检测并显示在上位机中。被控的电磁直线执行器工作行程为20 mm,线圈256匝,电阻为1.18 Ω,动质量为0.250 kg。

图6 试验平台Fig.6 Experimental setup
3.2 不同输入下性能分析
为验证优化后控制参数对控制性能的影响,根据优化所得鲁棒控制的控制参数,对优化前后电磁直线执行器的阶跃响应进行对比分析。在不同时间段设置不同期望位移,电磁直线执行器阶跃响应如图7所示。
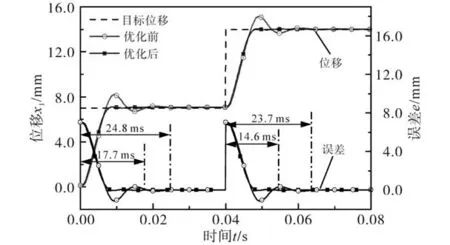
图7 不同目标位移阶跃响应优化前后曲线对比Fig.7 Comparison of curves before and after the step response optimization for different targets
由图7可知,优化前后的鲁棒控制都能实现系统对位置阶跃信号的跟踪,稳态误差趋于0;第一阶段,优化后电磁直线执行器达到98.0%参考位置的时间为17.7 ms,相比与优化前提升了28.6%;第二阶段,优化后电磁直线执行器达到98.0%参考位置的时间为14.6 ms,相比与优化前提升了38.4%,在保障稳态精度前提下,优化后的鲁棒控制的响应速度更快。阶跃信号中的JITAE由 1.7×10-6下降为 1.3×10-6,下降了约 23.5%;超调量σ由优化前的12.4%下降到了0.6%,下降了约95.2%。可以看出,采用多目标粒子群优化方法对本文鲁棒控制的控制参数的优化,有效降低了阶跃信号中的JITAE,同时显著降低了超调量σ。
为验证优化前后鲁棒控制的轨迹跟踪性能,对优化前后电磁直线执行器的正弦响应进行对比分析如图8所示。设置期望位移xd=7sin(2πt)mm,由图8可知整个跟踪过程中,优化前的鲁棒控制最大误差为0.17 mm,优化后的鲁棒控制最大误差为0.08 mm,降低了52.9%,优化后的鲁棒控制的跟踪误差,显著小于优化前鲁棒控制下的跟踪误差。正弦信号中的JITAE由 4.8×10-5下降为 8.7×10-6,下降了约 81.9%;相移量S由优化前的3.5×10-3rad下降到了7.10×10-4rad,下降了约79.7%。对比可知优化后的鲁棒控制不仅能够提高系统的瞬态响应性能,而且能够以更高的精度跟踪连续位置指令,实现平稳跟踪。

图8 正弦轨迹跟踪优化前后曲线对比Fig.8 Comparison of curves before and after sine trajectory tracking optimization
为验证优化后控制器跟踪斜坡信号效果,对优化前后电磁直线执行器的斜坡信号进行对比分析。图9为斜坡信号斜率xd=0.3 m/s,电磁直线执行器优化前后位移对比曲线。由图9可知,优化前的鲁棒控制最大误差和电磁直线执行器与目标位移进入同步的时间为分别为0.50 mm和38.2 ms;优化后的鲁棒控制最大误差和进入同步的时间为分别为0.32 mm和15.1 ms;最大误差相比于优化前降低了36.0%,进入同步的时间相对于优化前提高了60.5%。斜坡信号中的JITAE由3.37×10-8下降为 3.44×10-9,下降了约 89.79%;超调量σ由优化前的19.1%下降到了13.4%,下降了约29.8%。可以看出,采用多目标粒子群优化方法对本文鲁棒控制的控制参数的优化,有效降低了斜坡信号中的JITAE和超调量σ,提高了控制器的稳定性。

图9 斜坡跟踪优化前后对比Fig.9 Comparison before and after slope tracking optimization
4 结论
提出一种以系统控制器参数为优化变量,优化目标同时包括静态性能指标与动态性能指标:系统ITAE准则,正弦信号跟踪下的相移量,阶跃信号下的超调量;采用MOPSO对控制参数进行优化;求解Pareto前沿;利用pearson相关系数分析法控制参数与控制系统性能的相关系数矩阵;最后结合相关系数矩阵选择最终控制参数最优解,可提高控制参数调节的效率,降低控制器设计开发时间,具有一定的工程应用价值。
通过对优化后的控制参数进行试验验证,电磁直线执行器控制系统中JITAE下降了约79.9%;阶跃信号下超调量σ下降了约95.2%;正弦跟踪下相移量S下降了约79.7%。试验结果表明,优化后的控制参数能充分利用控制器的鲁棒性,提高电磁直线执行器动态响应特性,较好的满足控制要求,验证了优化的有效性与适应性。

