PFC直流电压控制性能提升的非线性控制策略
尹爱辉,任昂,武晓文,侯建峰,范玉林
(国网山东省电力公司济南供电公司,山东 济南 250002)
在交流系统中,功率因数低将导致线路电能利用率低,同时非线性负载带来的谐波电流会降低供电品质,易影响到其他负载设备的正常供电。因此,电网标准中定义了并网电流所允许的最大谐波含量,故用电设备非线性程度高时需使用功率因数校正器(power factor corrector,PFC)[1]。
PFC可由Boost变换器、Cuk变换器或Boost与Buck的级联变换器等实现[2-4]。基于Boost电路实现的PFC具有断续电流模式(discontinuous current mode,DCM)或连续电流模式(continuous current mode,CCM)两种运行工况。DCM因为无需测量电流,控制电路简单,但峰值电流高,故适用功率范围有限,通常为百瓦级。而基于CCM设计PFC则低功率下仍存在DCM工况,导致电流总谐波失真(total harmonic distortion,THD)增加,对此,文献[5]提出了一种调制载波控制,以改善PFC进入DCM模式后的电流波形。但只是从载波控制出发,对PFC的动态性能的提高存在局限。
PFC中常规使用的PI控制器存在固有局限,对此文献[6]中设计了PFC的分段自适应PI控制,保证了系统快速启动,但只是集中于电流跟踪,实际上由于电压控制回路直接控制峰值电流,直流侧纹波也将被引入并网电流中,产生谐波。为了抑制此谐波,文献[7]专门研究了给定谐波电流下,直流电压PI控制器在直流侧纹波频率范围内最大可实现增益,从而给出了电压闭环设计中允许电流谐波和电压动态的折衷规律。为了进一步提高PFC直流电压控制性能,文献[8]通过设置滤波以达到为控制器提供了更高增益的目的,但需要大量的信号处理,且PFC需要2至3个周波才能稳定运行。文献[9]设计了PFC无模型预测电流控制以提高负载动态响应,文献[10]设计了状态观测器来估计负载电流代替测量前馈,以改善负载瞬变期间直流电压的调节,但这些方案的复杂度均较高。
综上,本文提出了一种PFC直流电压控制性能提升的非线性控制策略。新方案的设计思路遵循Takagi-Sugeno型非线性模糊模型,并使用具有可变增益的PI控制器来实现。增益调整可极大地改善系统谐波性能,并获取与最优参数整定的线性控制器或复杂结构的非线性控制器接近的动态性能。
1 单相PFC的非线性PI电压控制器设计
图1为具有交错并联Boost电路的单相PFC。并联的Boost电路开关角差180°,使等效开关频率加倍以减小电流纹波。图1中,uAC为电源电压,用于电流参考生成和前馈;uDC为直流电压,用于电压控制反馈;i1和i2为开关电流;CDC为直流侧电容;L1和L2为Boost电路电感,整个PFC系统的运行目标是使并网电流跟踪电网电压波形,并保持直流电压稳定。

图1 单相PFC电路图Fig.1 Circuit diagram of the single-phase PFC
PFC采用双闭环控制。实际上,电流内环的带宽明显高于工频,故可对级联的电流和电压环分别进行设计,本文重点研究电压外环设计,以期减小谐波含量并改善系统动态性能,而电流内环则仍保持常规控制策略即可。
非线性PI电压控制器基于Takagi-Sugeno型非线性模糊模型结合PI调节器实现。Takagi-Sugeno型非线性模糊模型由线性子模型构成,然后将各线性子模型的输出加权。具有并行结构和加权的控制器可称为并行分布式补偿器(parallel distributed compensator,PDC),PDC以状态反馈形式给出:

式中:uout为PDC控制输出;r为加权函数的数量,在模糊逻辑控制相关表述中,加权函数也称为隶属函数[11];Mi为用于计算输出的加权函数;Ki为对应的控制增益;x(t)为系统状态变量。
图2为基于PDC的非线性PI电压控制器框图。其中uref为直流电压参考;M1和M2为加权函数;PI1和PI2为两组PI调节器,两者的比例和积分增益分别为KP1和KP2,以及KI1和KI2,加权后的总比例和积分增益为KP和KI;KIL为电流环增益;GU和GI分别为电压开环和电流开环模型。

图2 非线性PI电压控制器框图Fig.2 Block diagram of nonlinear PI voltage controller
图3为加权函数M1和M2的设计图,图中m1和m2为控制器不同运行区的边界。当直流电压测量值和参考间的误差绝对值|e|位于区域Ⅰ中时,系统调整为低带宽控制器来确保低谐波含量;当|e|位于区域Ⅲ中时,系统改为使用高增益控制器来加快负载扰动时收敛速度;当|e|位于区域Ⅱ时,控制则换成高增益控制器和低增益控制器的输出加权和,而权重则取决于误差大小。区域Ⅱ中的加权设计允许控制器从低增益到高增益平滑过渡。

图3 加权函数设计图Fig.3 Weighting function design diagram
图4为非线性比例增益KP的变化曲线图,图中虚线代表KP1和KP2,实线则代表最终控制器使用的KP。值得注意的是,控制器积分增益具有和比例增益相同的变化趋势,故不再累述。

图4 非线性增益变化曲线图Fig.4 Curves of the nonlinear gain change
控制器不同增益下对应区域的宽度需合理设计,以便在满载情况下,直流电压纹波幅值符合要求,同时确保系统处于稳态时,非线性增益不产生额外的电流谐波。
2 非线性PI电压控制器的实现
以直流侧输入电流iDC为输入,uDC为输出,可建立uDC控制模型为

式中:CDC为直流电容;R为负载电阻。由于电压控制目标是使直流电压uDC无静差跟踪参考电压uref,即将两者的误差调节为零,故系统状态可设为uDC和uref间的误差e如下:
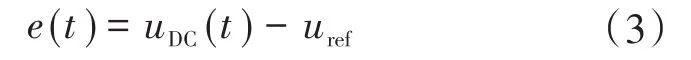
将e作为状态变量,iDC作为输入,则有:

由于系统使用了积分控制器进行控制,因此模型利用积分器状态扩展,常规PI控制器可描述为

式中:ω为积分器状态。
由式(4)、式(5)可推导状态空间形式描述为

进一步,使用非线性PI控制后,式(5)替换为

引入M1和M2后,当e<m1或e>m2时,仅使用单一常规PI控制器即可,此时,系统行为仍可用式(6)描述,并使用诸如极点配置等成熟的控制器设计方法进行参数设计,并采用伯德图进行分析。因此,非线性控制仅在m1<e<m2时与传统PI控制方案不同。
边界值m1和m2用于调整控制器的增益,故加权函数M1和M2可设计为

值得注意是,相对于其他非线性控制器,基于由PDC设计的非线性PI电压控制器的优势之一在于其结构更为简单、复杂度低,仅使用两个常规PI调节器结合两组比较器、乘法器、求和和绝对值计算即可实现。
非线性PI电压控制器的参数设计可采用以下步骤进行整定:1)基于所需的直流电压动态,整定KP2和KI2;2)将KP2和 KI2减小1倍后作为稳态PI控制器增益 KP1和KI1;3)将 m1设置为满载直流电压纹波峰峰值的50%;4)边界m2则设置为2倍的m1。采用上述步骤设计非线性电压PI控制器参数后,可使得控制器具有常规PI调节器的动态性能,并改善了稳态输出。
3 稳定性分析
下面对基于PDC的非线性电压PI控制器的稳定性进行分析。在PDC控制器的表述式(1)中,若r>1,则系统将由多个线性模型描述,此时Lyapunov不等式可写为以下形式:

式中:Ai为子系统状态矩阵;P为公共矩阵。
P构成了二次型Lyapunov函数V如下:

式中:x(t)为系统状态向量。
若存在一个正定矩阵P,对任意i,均使得式(11)成立,则可证明由几个子系统组成非线性系统的稳定性。
与其他非线性控制器相比,由PDC设计的非线性PI电压控制器的优势之二在于可使用数值求解器直接找到公共正定矩阵P[11]。式(11)可通过线性矩阵不等式求解。实验系统参数设置如下:Boost电路电感 L1=L2=500 μH,额定直流电压 UDC=405 V,直流电容 CDC=1 500 μF,控制频率fctrl=5 kHz,PFC额定功率PN=3 kW,电网电压UN=220 V,比例增益KP1=0.391 9,比例增益KP2=0.783 7,积分增益KI1=34.074 1,积分增益KI2=68.148 1,误差边界m1=7.8 V,误差边界m2=15.6 V。
基于实验系统参数,系统稳定性可通过数值计算闭环系统Ai对应的公共正定矩阵P来证明,因为P可使得式(11)中给出的Lyapunov不等式成立。假设PFC空载运行,则负载电阻R=∞,式(6)所描述的系统可写为矩阵形式:
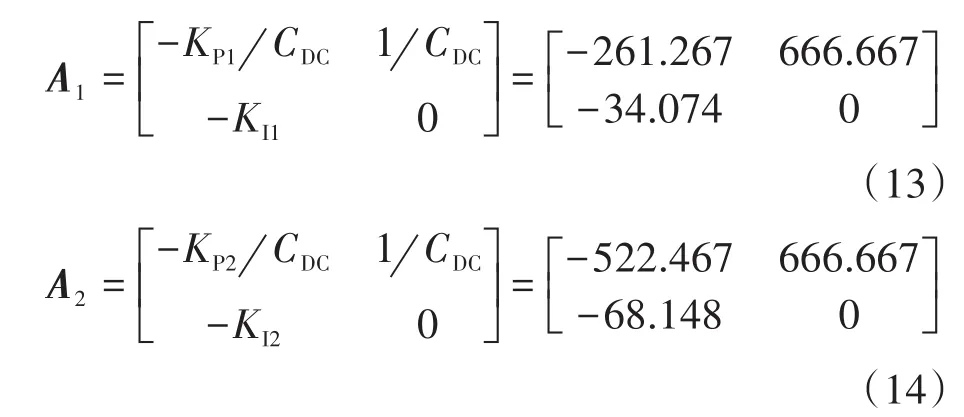
通过数值计算可求解得到公共正定矩阵P如下:

将P代入式(12)可证明Lyapunov不等式成立,从而非线性电压PI控制器的全局稳定性得到证明。
4 实验验证
为验证非线性电压PI控制器的性能,搭建了3 kW的PFC试验样机开展实验研究,如图5所示,主要包括Boost电路和开关电流传感器、直流电容,EMI滤波器和数字控制器等。交流侧设有整流电路和Boost电路。直流侧设置等功率的移相全桥变换器。由于全桥变换器的动态响应比直流侧电压快很多,故实验中突加负载测试主要还是考核PFC的直流电压控制性能。系统参数设置同第3节。数字控制器由ST具有32位ARMCortex-M4F内核的STM32F407实时控制芯片和Xilinx的FPGA(Spartan-6)配合构建。测试中使用安捷伦DSO6104A示波器、泰克PS5210差分电压探头和安捷伦N2781A(150 A/10 MHz)电流探头进行电量采集。

图5 PFC实验样机Fig.5 Experimental prototype of the PFC
系统动态采用负载突变来进行测试,即负载从150 W→2.4 kW和2.4 kW→150 W阶跃变化来考核系统。
图6为负载从150 W→2.4 kW时的并网电流ig和uDC波形。由图6b可知,当误差e大于7.8 V后转为非线性增益,并在t=150 ms突加负载后,耗时2个工频周期达到稳态。对比测试结果表明,非线性增益的使用,实现了新控制器与常规线性PI控制器一致的ig和uDC动态。

图6 突加负载实验结果Fig.6 Experimental results of the sudden increasing load
图7为ig有效值为9.6 A时的稳态电网电压和电流波形,图中可观察到电流波形存在过零点失真,这是由占空比限制引起的,即软件中限制了占空比最大值为0.8,该限制是为了确保在任意工况下,电流互感器有足够时间复位。

图7 稳态实验结果Fig.7 Experimental results at the steady-state
图8a、图8b分别为负载从2.4 kW→150 W时的ig和uDC波形,其中包含了两种控制器的对比结果,类似于突加负载动态,两种控制器的动态性能一致。值得注意的是,当直流电压超过420 V时,由于PFC无法将功率反馈给电网,故停止运行,而此时非线性PI电压控制器的超调要更小,但这不是由控制器性能差异导致的,而是取决于动态时电网电压相位。

图8 突卸负载实验结果Fig.8 Experimental results of the sudden dumping load
进一步,对电流的THD进行分析来评估非线性PI电压控制器对并网电能质量的影响。图9a、图9b分别为常规线性PI电压控制器和非线性PI电压控制器配置下的电流谐波频谱和THD,谐波分析时的系统功率为2.4 kW,THD由FFT分析出的前40次谐波进行计算得到。从图9可看出,两种控制器主要生成了3次谐波和少量的高次谐波,但非线性PI电压控制器作用下的3次谐波将大为降低,这与图6a和图8a中的稳态电流波形相互映证,传统控制器作用下的电流峰值更高,这主要就是3次谐波导致的。此外,图9表明在线性PI电压控制器作用下,THD为12.36%,而非线性PI电压控制器可将THD降至6.13%,新方案可将电流THD提高50%以上。

图9 电流谐波对比实验结果Fig.9 Experimental results of current harmonics comparison
图10为PFC系统的功率因数PF随负载功率P的变化曲线,图中当负载功率大于0.75 kW时,PFC的功率因数接近于1,这和图7中ig有效值为9.6 A时的电压电流相位一致相互映证。

图10 功率因数随负载功率的变化曲线Fig.10 Curve of power factor change with load power
表1中汇总了两种控制器的性能对比,对比结果验证了非线性PI电压控制器取得和常规线性控制器相当的动态性能时所具有的稳态性能优势。

表1 两种控制器性能对比Tab.1 Performance comparison of two controllers
5 结论
围绕PFC直流电压控制性能提升,本文设计了一种基于PDC的非线性PI电压控制器。其与常规的线性PI控制器相比,在系统稳态时获取了电流低谐波含量,且保留了较快的负载动态响应速度。同时,新控制器较其他非线性控制器结构更简单,参数整定相对容易,稳定性也可由数值求解得到证明。
对比实验测试结果表明,所提出的非线性PI电压控制器在负载大扰动下只耗费2至3个工频周期即可使系统达到稳定状态,且较之传统线性PI控制方案,电流THD可降低50%。

