基于模态试验的PCB板结构动态性能的等效建模

汤贺鑫，张 巍，管照阳，刘 愚，郭小军，罗凤旺，李 江，张 莹

基于模态试验的PCB板结构动态性能的等效建模

汤贺鑫，张 巍，管照阳，刘 愚，郭小军，罗凤旺，李 江，张 莹

（昆明物理研究所，云南 昆明 650223）

PCB因其基板内部结构的复杂性以及元器件种类众多且分布无规律性导致有限元模型建立困难，为此本文针对某车载热像仪主处理板上元器件的分布及结构特点，提出了一种基于自由模态试验数据的PCB板动态性能等效建模的方法。该方法对基板采用其原几何尺寸建立，对元器件的处理方式根据其物理属性以及在基板上分布特点按不同方法处理，最终需保持等效模型的质量与实际相等，并利用了自由模态试验数据以及最小二乘法推导出了基板的等效刚度以及泊松比的计算方法。通过正弦扫频试验获取主处理板的响应曲线，利用半功率带宽法计算前两阶响应对应的阻尼比，将阻尼比有限元分析软件中，获得等效模型数值计算的响应曲线，与试验的响应曲线对比，结果表明该等效建模方法满足实际工程需求，为类似产品的等效建模提供了可借鉴的思路。

PCB；等效模型；模态试验；半功率带宽法

0 引言

热像仪在执行任务时，面临着振动、冲击、高温等恶劣环境的考验。而热像仪内部的主处理电路板作为实现电信号传输、采集、转换以及电控制的重要载体[1]，其是否能承受振动环境的考验决定着热像仪在振动环境下的整机性能。

有限元分析是展开印制电路板（printed circuit board，PCB）的结构动态性能研究的一种常用方法[2]。PCB的结构动态性能，会因其覆铜层数、电路布局以及制造中使用不同聚合物材料而有所不同，PCB上元器件分布无规律性也增加了对PCB进行全面建模的难度[3]。同时对设备进行整机分析时，并不关注PCB内部以及元器件的结构动态性能[4]，因此寻求等效模型对PCB展开研究是合理的方案。

目前，国内外对PCB的等效建模方法进行了大量的研究。Pitarresi J M对比分析了5种PCB有限元等效建模方法[5]，其中频率计算较为精准，实现难度较大。Wu等人采取静力学试验校准电路板的等效有限元模型的材料参数[6]，此种方法操作繁琐且成本较高。针对PCB等效模型，刘孝保等构建了基于试验数据获取等效刚度的计算方法[7-8]，但试验数据为约束状态下测得，因此此种方法等效刚度会引入约束条件带来的误差。

本文针对某车载红外热像仪的主处理电路板建立等效有限元模型。提出了一种基于电路板自由模态的试验数据，以保持等效模型的质量、固有频率与实物相等的原则，获取考虑元器件分布的电路板结构等效模型的材料参数，将获取的等效参数代入等效模型中从而完成等效模型的搭建。通过对电路板在约束状态下进行振动试验，与等效模型在有限元分析软件计算结果对比，证明该等效方法的正确性。

1 主处理板结构动态性能等效模型

1.1 等效建模的基本思路

此次分析的对象为某型热像仪的主处理电路板，如图1所示。其基板的主要尺寸为208mm×175mm×2mm，基板上附有功能芯片、接插件以及大量的表贴器件、电阻、电容、电感等部件。为保证计算结果的准确性与计算时长的可观性，因此考虑主处理板上主要的元器件分布的影响建立等效模型，其等效模型的几何模型如图2所示，保证了电路板上主要元器件的基本尺寸的一致性。

一般以结构的固有频率作为结构动态性能的评价指标，因此主处理板的等效模型需保持等效电路板模型与实物质量及其分布相等和等效模型的固有频率与实物相等。基于以上原则，考虑接插件、功能芯片等元器件的质量及刚度对基板的影响；考虑较轻元器件集中分布区域（如图1椭圆标记的两处）的质量对基板的影响；考虑将尺寸质量较小且分布均匀的电阻电容等元器件质量均匀附着在基板上。因此等效模型的数学模型可表示为：

(b,x,y,z,1,2;b,x,y,z;b,x,y,z,

1,2;b,x,y,z)≈0(1)

式中：为模态频率；为模型几何尺寸；为材料杨氏模量；为材料密度；为泊松比；下标b表示主处理板基板模型；下标x、y、z分别表示金属封装芯片、塑封芯片、接插件模型，下标1、2分别表示图2中“[1]、[2]”区域的模型，下标0表示实测数据。

图1 主处理电路板

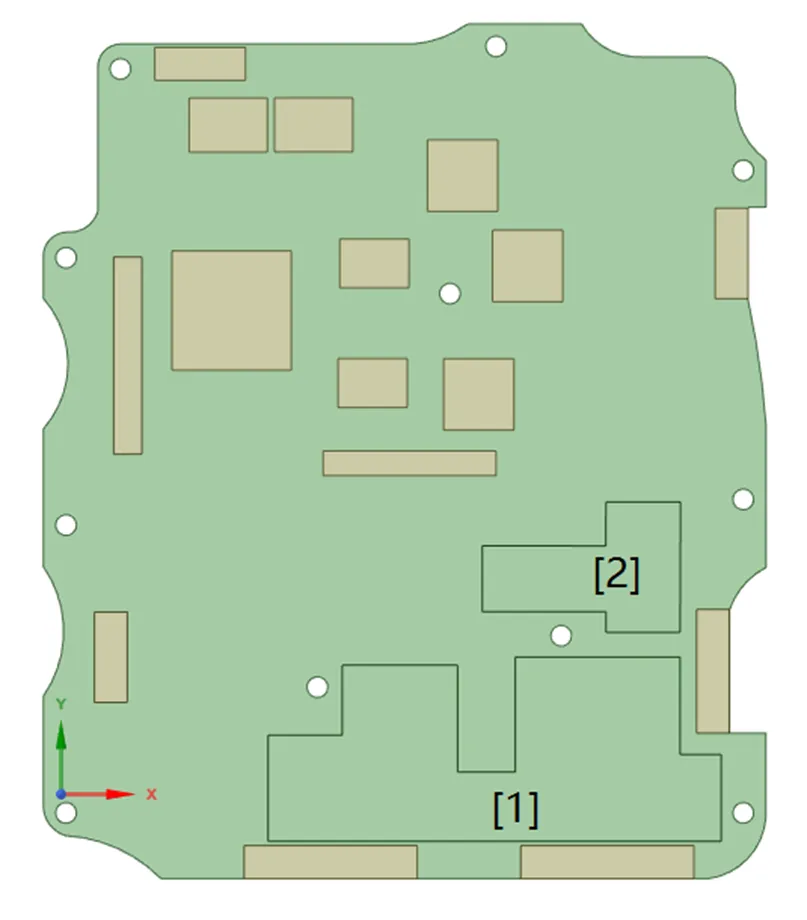
图2 主处理板等效模型

＝M/V(2)

式中：表示模型质量。当＝x, y, z时，M通过精密天平称重获取；当＝b时，b＝a－åx－åy－åz－1－2，其中a表示主处理板总质量，å表示该类元器件的质量总和，1、2分别表示“[1]、[2]”区域上元器件质量总和；当＝1, 2时，＝b＋M/V，M通过精密天平称重获取。

各元器件的、值参考文献[9-10]中的取值，其中“[1]、[2]”区域仅考虑其质量的影响，因此其、与基板值取同。经整理计算各参数的取值如表1所示。

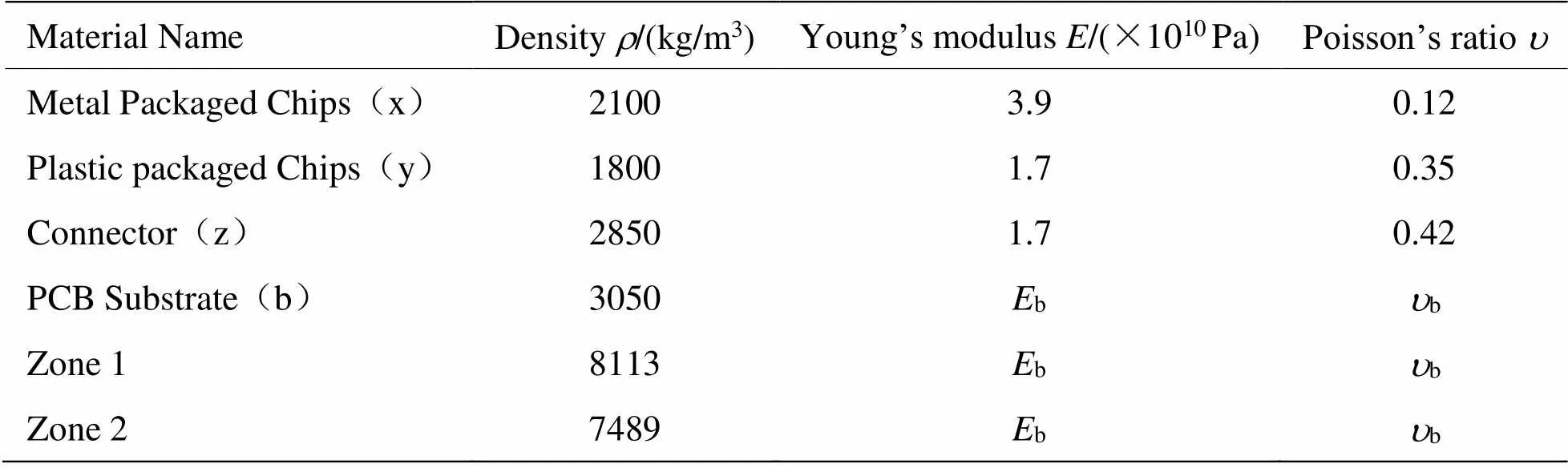
表1 材料参数

由此式(1)表达式可退化为：

县乡两级管理互通互融，县农口有关部门与乡镇街道农技推广班子定期联络，县农口有关部门多走访，乡镇街道农技推广班子多汇报，互通信息，细致管理，切实做好农技推广业务工作并及时落实到位，切实实现工作职责，避免推广工作行政化，以及行政事务替代本职工作现象，着力避免农技推广工作脱离农民现象［3］。共同服务新型职业农民培育、壮大新型农业经营主体的农技推广新模式。

(b,b)≈0(3)

1.2 等效杨氏模量和泊松比推导

为获取等效模型基板的杨氏模量和泊松比，首先对主处理板进行自由边界条件下的模态试验，使用橡皮筋悬挂主处理板如图3所示，通过力锤敲击图4中叉号标记的16个点，获取这16个点锤击力和加速度响应，对测量的锤击力和加速度响应之间的频率响应函数进行曲线拟合，以提取主处理板的试验模态参数，试验获取的模态频率结果如表2所示。

图3 自由模态试验电路板悬挂示意图

图4 力锤敲击位置标记示意图

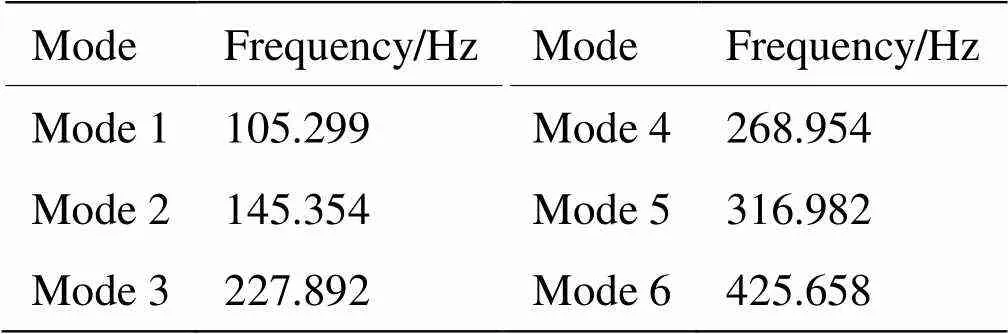
表2 自由边界条件下试验测得主处理板的前六阶模态频率

由式(3)所表述的函数关系，设计变量按照杨氏模量、泊松比的顺序分别针对数值和试验固有频率之间的最小平方误差总和进行优化[11]，即：

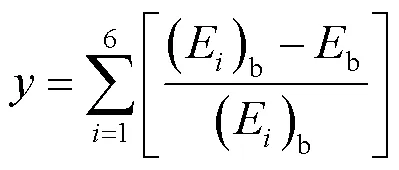
式中：(E)b为拟合第阶试验固有频率对应的杨氏模量；b为考虑6阶频率的杨氏模量。

使得取最小值，则：

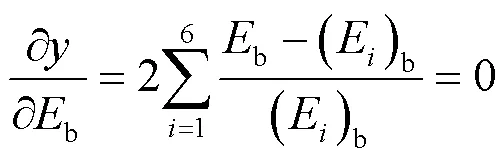
由式(4)可求得6阶频率下的等效基板杨氏模量为：

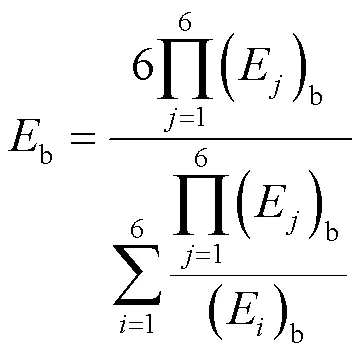
同理6阶频率下的等效基板泊松比为：

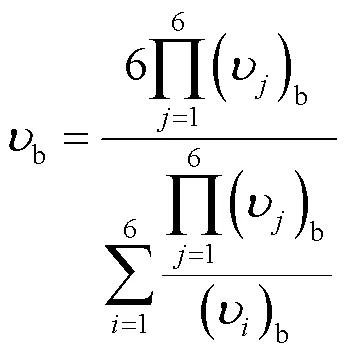
式中：()b为基板杨氏模量取得等效基板杨氏模量b后，拟合第阶试验固有频率对应的泊松比，b为考虑6阶频率的泊松比。

获得基板的杨氏模量与泊松比：b＝20Gpa，b＝0.48。将获取的材料参数代入等效模型中，并通过有限元分析软件进行求解。求解采用的网格为四面体与六面体网格相结合的网格划分方式，最终网格单元数为44513，网格节点数为107165，并在数值计算过程，进行了网格无关性验证，将网格单元数增至原来的2倍左右，前6阶频率结果偏差在1%以内。得到的自由边界条件下的主处理板前6阶模态结果并与试验模态结果对比，如表3所示。

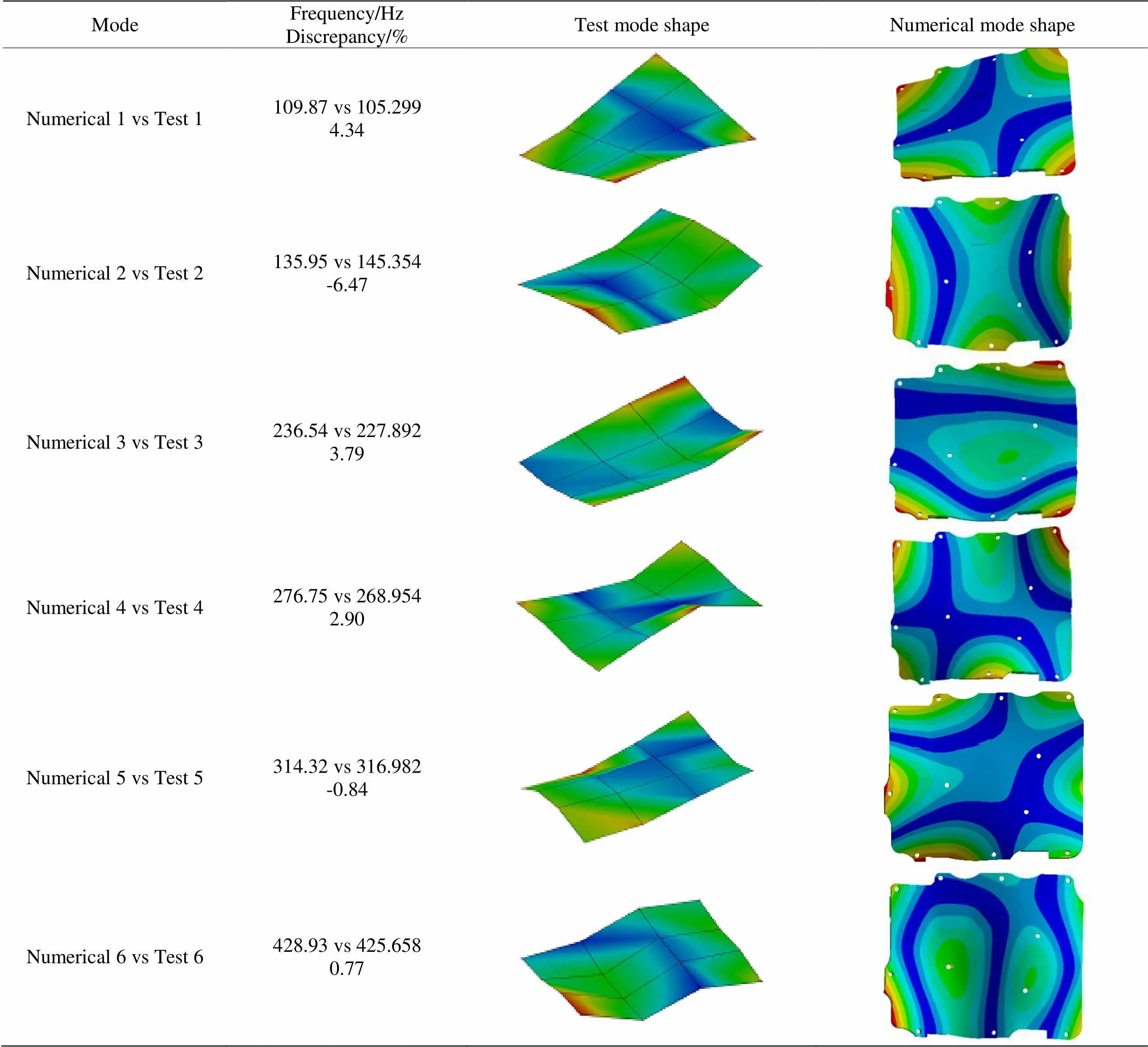
表3 自由边界条件下试验与数值计算的主处理板前6阶模态

从表3可以看出自由模态下，运用最小二乘法校准基板杨氏模量与泊松比后，数值计算与试验结果相比，前六阶固有频率的相对误差最高6.47%。且由表3可知，数值计算和模态试验的振型吻合良好，因此通过模态试验测得的频率校准等效模型参数是有效的。

2 主处理电路板正弦激励响应

为验证通过自由模态试验获得等效参数后的主处理电路板等效模型的准确性，对主处理板在约束状态下进行扫频振动试验，并与有限元分析软件计算结果对比。

在对主处理板进行正弦扫频试验时，先将主处理板通过螺栓安装在金属工装上，并将工装通过压板与垂直振动台进行连接，加速度传感器布置位置为主处理板末端两接插件之间，如图5所示，此位置对应有限元分析软件解算的一阶响应最大位置。

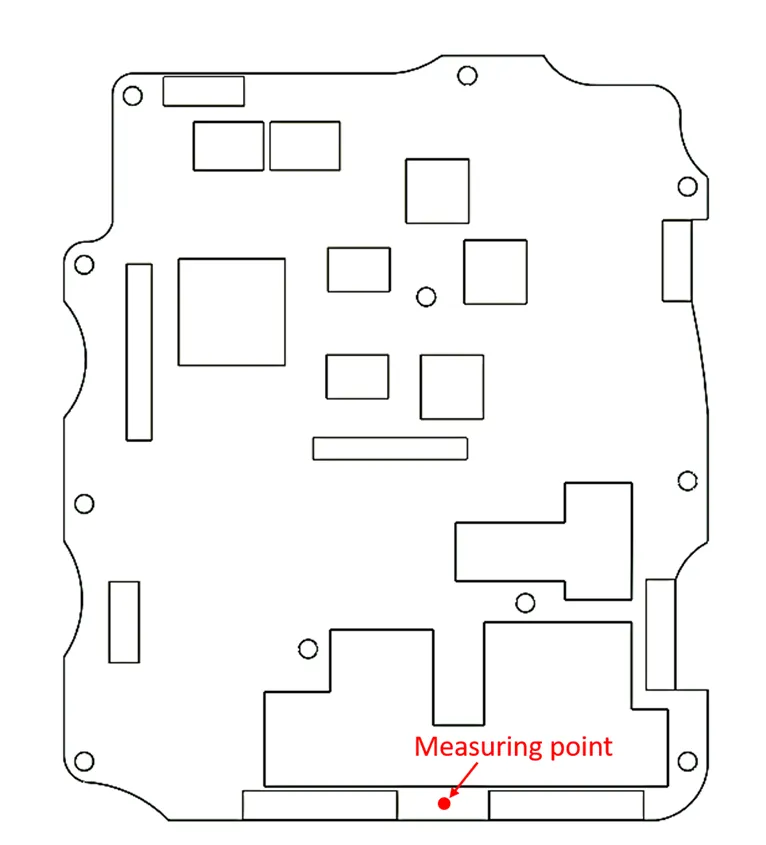
图5 传感器安装位置示意图

振动台输入激励的大小为1，扫频范围为10～1000Hz，扫频速率为1oct/min，通过东华的测试软件获得测点振动响应曲线图，如图6所示。

通过图6可以确定约束状态下前两阶频率，由于该主处理板应用环境为车载环境，其振动环境适应性要求最高频率为500Hz[12]，因此获取的前两阶频率满足实际要求。

在测得的频谱图中，可以通过半功率带宽法估计各阶响应的阻尼比[13]：

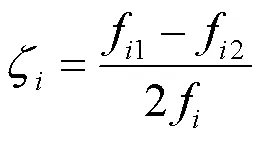
式中：zi表示第i阶响应对应的阻尼比；fi1、fi2表示该阶共振频率幅值2－1/2处对应的频率值，其中fi1＞fi2，fi1－fi2为半功率带宽；fi表示该阶共振频率。

由式(8)以及频谱图数据算得，一、二阶的阻尼比分别为1≈1.04%、2≈0.90%。

在有限元分析软件对主处理板进行动态分析时，采用梁单元代替螺栓连接，梁单元直径取螺栓公称直径3mm，主处理板等效模型的材料参数取表1数据，其中由自由模态试验获得等效参数b＝20Gpa,b＝0.48。主处理板的约束状态等效模型如图7所示，其中电路板的网格划分与此前解算自由模态取相同方式，螺栓梁则取其长度的1/10进行划分。

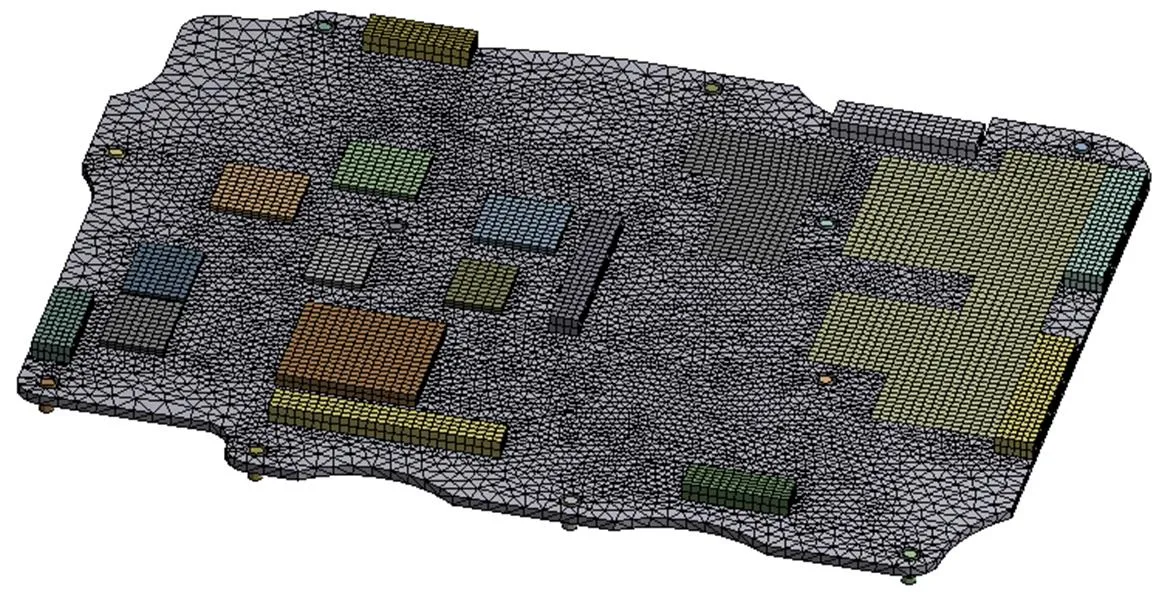
图7 主处理板约束状态等效模型

在模态分析中10～1000Hz内有6阶模态，而试验获得的响应曲线后4阶频率值不好判断，因此通过半功率带宽法仅能获取前两阶的阻尼比，为使得计算响应曲线更符合实际，其他阶的阻尼比均取0.5%，将各阶阻尼比输入ANSYS软件谐响应分析模块中，获取试验测点位置对应的网格节点处的频率及加速度响应幅值，并将数据坐标值双对数化处理得到测点的振动响应曲线图，如图8所示。

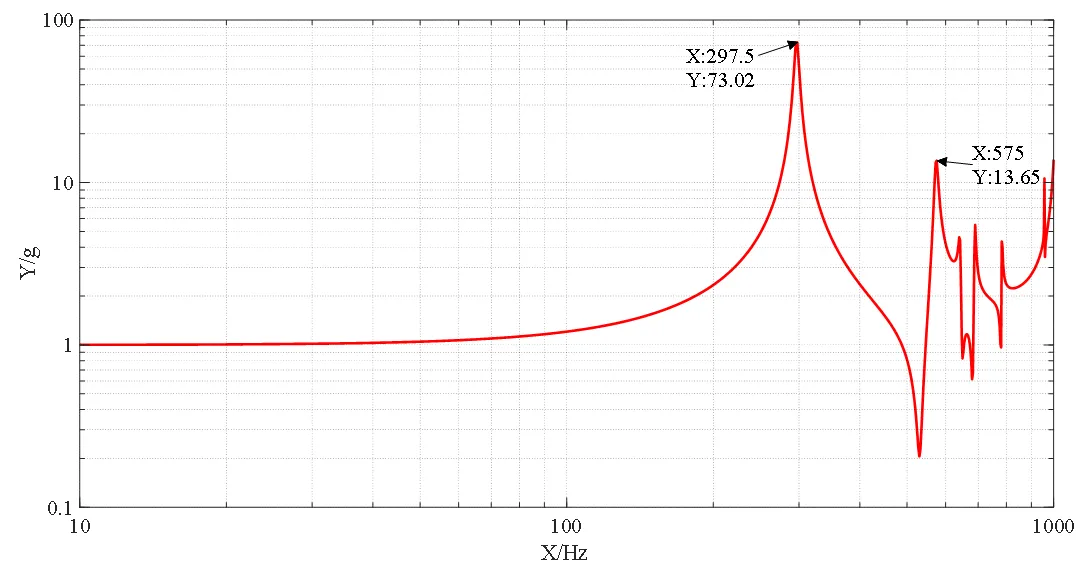
图8 通过有限元分析软件计算的测点振动响应曲线图

由图6和图8可以看出，试验与有限元分析软件计算结果的测点振动响应从曲线形状上看拟合度较高。对比试验与数值计算数据结果，前两阶频率、峰值响应以及误差如表4所示。

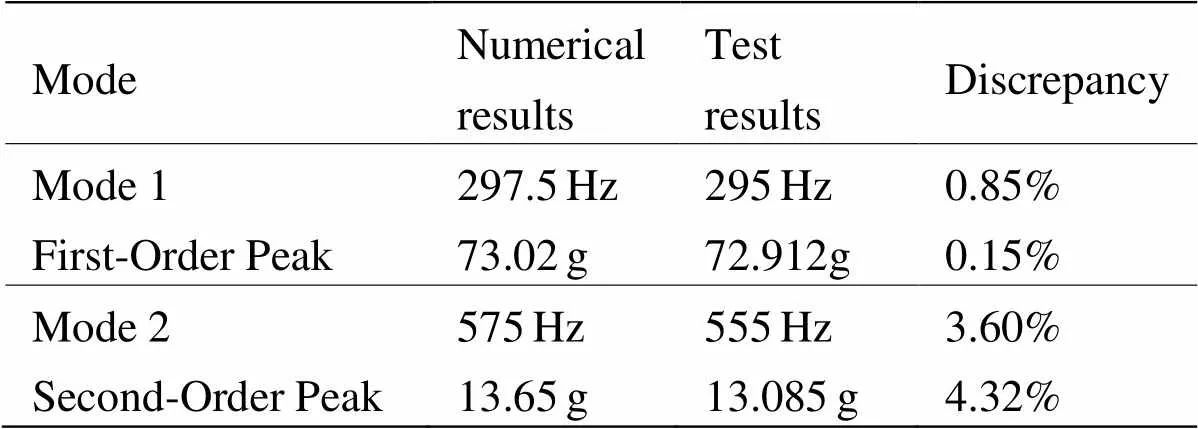
表4 约束状态下主处理板等效模型的频率、峰值响应以及误差

由表4可以看出，通过自由模态试验获得等效参数后的主处理电路板等效模型在约束状态下，不论在频率以及峰值响应与试验的相对误差都小于5%，满足工程精度要求。

3 结论

根据热像仪主处理板上元器件的分布以及结构特点，提出了一种基于自由模态试验数据的PCB板动态性能等效建模的方法。该方法基于PCB基板的几何尺寸以及元器件的分布，并利用自由模态试验数据以及最小二乘法得出基板的等效刚度以及泊松比的计算方法。通过正弦扫频试验获取主处理板的响应曲线，利用半功率带宽法计算前两阶响应对应的阻尼比，将阻尼比代入有限元分析软件中，获得等效模型数值计算的响应曲线，与试验实测响应曲线对比，结果表明该等效方法满足实际工程需求，为类似产品的等效建模提供了可借鉴的思路。

[1] 陶亮, 赵劲松, 刘传明, 等. 高可靠性红外热像仪的设计方法[J]. 红外技术, 2014, 36(12): 941-948.

TAO Liang, ZHAO Jinsong, LIU Chuan-ming, et al. Design methods of high reliability thermal imagers[J]., 2014, 36(12): 941-948.

[2] 尹俊辉, 徐立, 杨再超, 等. 基于有限元方法的印制电路板的模态分析[C]//中国力学大会-2017暨庆祝中国力学学会成立60周年大会论文集, 2017: 233-238.

YIN Junhui, XU Li, YANG Zaichao, et al. Modal analysis of the PCB base on finite element method[C]//- 201760th, 2017: 233-238.

[3] LEE Y C, WANG B T, LAI Y S, et al. Finite element model verification for packaged printed circuit board by experimental modal analysis[J]., 2008, 48(11-12): 1837-1846.

[4] 姜宇, 肖鸿, 刘兴鹏, 等.一种新型宽带单面异向介质结构的分析与设计[J]. 电子测量与仪器学报, 2009(8): 27-31.

JIANG Yu, XIAO Hong, LIU Xingpeng, et al. Analysis and design of novel broadband metamaterial structure[J]., 2009(8): 27-31.

[5] Pitarresi J M, Primavera A A. Comparison of modeling techniques for the vibration analysis of printed circuit cards[J]., 1992, 114(4): 378-383.

[6] WU J, ZHANG R R, Radons S. Vibration analysis of medical devices with a calibrated FEA model[J]., 2002, 80(12): 1081-1086.

[7] 刘孝保, 杜平安, 夏汉良, 等. 一种面向动态分析的PCB板等效建模方法[J]. 仪器仪表学报, 2011(4): 145-151.

LIU Xiaobao, DU Ping'an, XIA Hanliang, et al. Dynamic property analysis-oriented PCB equivalent modeling method[J]., 2011(4): 145-151.

[8] 刘孝保, 杜平安. 基于实验的PCB板动态性能等效建模方法[J]. 电子科技大学学报, 2013, 42(5): 787-790.

LIU Xiaobao, DU Ping'an. Equivalent modeling method of PCB for dynamic property based on experimental data[J]., 2013, 42(5): 787-790.

[9] TANG W, REN J, FENG G, et al. Study on vibration analysis for printed circuit board of an electronic apparatus[C]//2007, 2007: 855-860.

[10] Karthiheyan S, Verma V K, Saravanan S, et al. Dynamic response characteristics and fatigue life prediction of printed circuit boards for random vibration environments[J]., 2020, 20(4): 920-929.

[11] 杨强, 杜平安, 周元, 等. PCB板动态分析等效建模方法[J].电子科技大学学报, 2015(3): 475-480.

YANG Qiang, DU Ping'an, ZHOU Yuan, et al. Equivalent modeling method for PCB’s dynamic property analysis[J]., 2015(3): 475-480.

[12] 施荣明, 朱广荣, 吴飒, 等. 军用装备实验室环境试验方法第16部分: 振动试验[S]. GJB 150.16A-2009.

SHI Rongming, ZHU Guangrong, WU Sa, et al. Laboratory Environmental Test Methods for Military Materiel-Part 16: Vibration Test[S]. GJB 150.16A-2009.

[13] Singiresu S Rao.机械振动[M]. 4版, 北京: 清华大学出版社, 2009. Singiresu S Rao.[M]. Fourth Edition, Beijing: Tsinghua University Press, 2009.

Equivalent Modeling of PCB for Dynamic Properties Based on The Modal Test

TANG Hexin，ZHANG Wei，GUAN Zhaoyang，LIU Yu，GUO Xiaojun，LUO Fengwang，LI Jiang，ZHANG Ying

(Kunming Institute of Physics, Kunming 650223, China)

It is difficult to establish a finite element model for a PCB owing to the complexity of the internal structure of the substrate, the large variety of components, and irregular distribution. To solve these issues, this article proposes the distribution and structural characteristics of the components on the main processing board of a vehicle thermal imaging camera as an equivalent modeling method of PCB board dynamic performance based on free modal test data. This method uses the original geometric size of the substrate and the components are processed in different ways according to their physical properties and distribution characteristics on the substrate. Finally, the quality of the equivalent model must be kept equal to the actual model, and the free mode is used. The experimental data and least square method were used to deduce the equivalent stiffness of the substrate and the calculation of Poisson's ratio, respectively. The response curve of the main processing board was obtained through a sine frequency sweep test. The damping ratio corresponding to the first two-order responses was calculated using the half-power bandwidth method, and the damping ratio finite element analysis software was used to obtain the response curve of the equivalent model numerical calculation. A comparison of the response curves shows that the equivalent modeling method meets the actual engineering requirements and provides a reference for the equivalent modeling of similar products.

PCB, equivalent modeling, modal testing, half-power bandwidth method

TN214

A

1001-8891(2022)03-0225-06

2021-09-06；

2022-01-14.

汤贺鑫（1997-），男，硕士研究生，主要研究方向：光机结构系统设计及仿真。Email：845477573@qq.com。