大学生方程式赛车电子差速控制策略研究

王淑旺,夏麒翔,罗建辉

(1.合肥工业大学 机械工程学院,安徽 合肥 230009; 2.合肥工业大学 汽车与交通学院,安徽 合肥 230009)

0 引 言

大学生方程式赛车大赛电车赛要求以院校为单位,自主设计并制造出一台满足赛事规则要求及安全要求的纯电动赛车,此赛车应在加速、刹车、操作性等方面性能优异且稳定[1]。本研究团队设计的赛车为双电机后轮驱动,两侧电机经减速器后将动力传递给车轮。这种设计去除了传统的机械差速器,使传动系统效率得以提高,且体积和质量大为降低[2]。因此,必须设计出电子差速算法以契合赛车传动系统,这在整车性能提升上显得尤为重要[3]。赛车选用Stm32f4系列单片机进行整车控制,此款单片机性价比较高[4],但性能上不适合进行复杂的数字信号处理,故在电子差速算法的设计过程中应充分考虑[5]。

针对该问题,国内外学者展开了大量研究。文献[6]提出了一种基于轮胎滑转率分配扭矩的算法,可以起到差速目的,但是滑转率误差会导致分配不合理;文献[7]提出了四轮独立驱动电动车识别不同工况并做出相应处理的电子差速算法,但该算法不适合本次设计赛车的硬件结构;文献[8]基于2片51单片机实现了车速估测及差速转向,该方式有一定的意义，但存在继续优化的空间;文献[9]提出了一种基于Ackermann-Jeantand模型的转速控制算法,该算法在低速时效果优异,但高速行驶工况及传感器测量误差均有可能使得车辆失稳。

电子差速算法目前有扭矩控制和转速控制2种设计思路[10-11],本文综合考量各因素,设计一种以质心侧偏角为控制依据、横摆角速度为控制目标的控制算法。该算法采用电子差速2种思路中的扭矩控制,针对底盘低且过弯速度快的小型赛车而设计,创新性地将质心偏移角作为依据,使用横摆角速度作为最终控制目标,确保车辆转向过程中的快速性及稳定性[12]。最后使用Matlab/Simulink整车模型仿真以及整车试验验证该算法的可靠性。

1 考虑质心偏移的扭矩分配

车辆在直线行驶过程中,由于赛道平坦且无阻碍,车辆的质心侧偏角可以忽略。而在转向过程中,汽车由于惯性的作用会产生一定的侧倾[13],导致外侧车轮载荷大于内侧车轮载荷(本文假设车辆左转,右转同理),如图1所示。

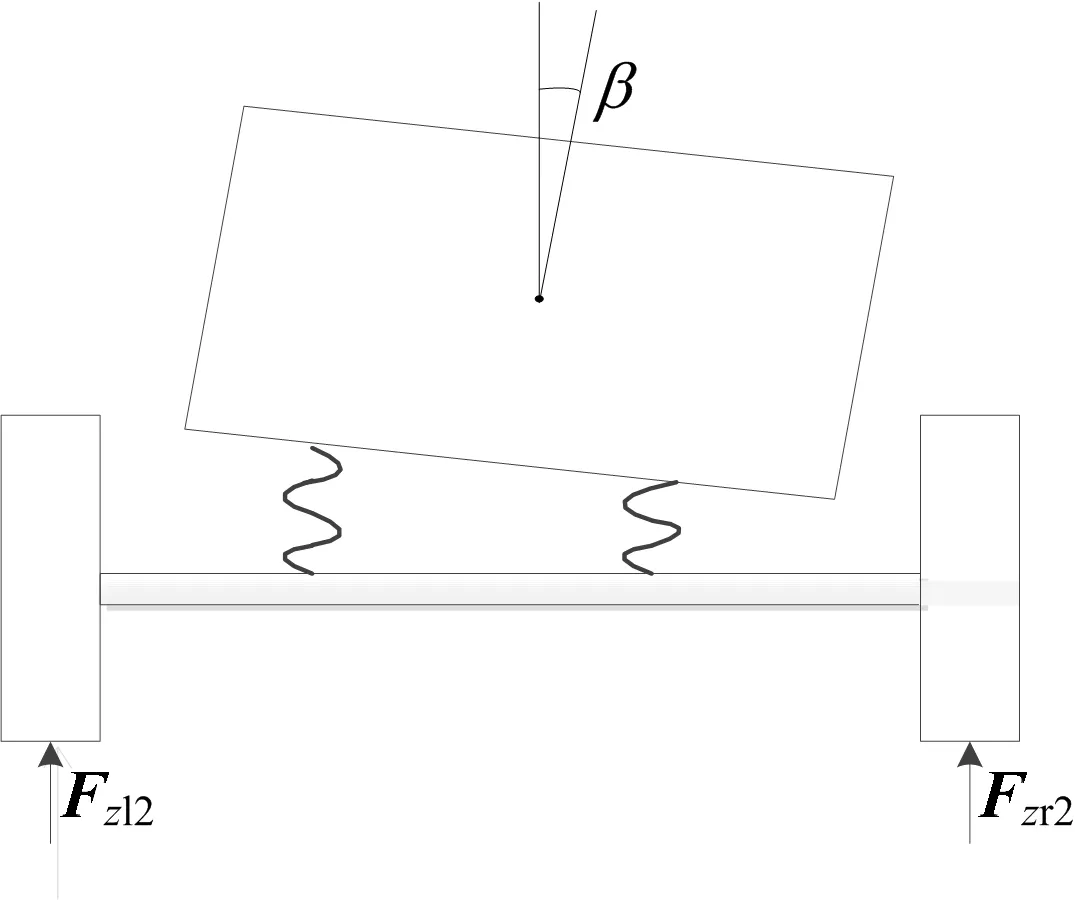
图1 转向时内外侧车轮载荷示意图

前、后车轮纵向载荷变化量计算公式为:

ΔFz1=2(msbhu2+musLhuu2+

ΔFz2=2(msahu2+musLhuu2+

(1)

其中:ms为簧上质量;mus为簧下质量;a为质心到前轴距离;b为质心到后轴距离;h为簧上质量质心高度;hu为簧下质量质心高度;u为纵向速度;K1为前悬架侧倾刚度;K2为后悬架侧倾刚度;β为侧倾角;L为轴距;θ为前轮平均转角。

同时,赛车4个车轮的静态载荷已知,则车轮转向时的载荷计算公式为:

(2)

其中:Fzl1为左前轮转向载荷;Fzr1为右前轮转向载荷;Fzl2为左后轮转向载荷;Fzr2为右后轮转向载荷;F1、F2为静态载荷,通过测量得到F1、F2分别为645.036、954.814 N。

车辆转向过程中由于质心侧偏会导致两侧车轮纵向载荷不等,进而外侧车轮阻力增大,内侧车轮阻力减小[14]。这就要求整车控制过程中,内、外侧电机扭矩需要适当调整,此举可以在优化转向性能的同时抑制车轮滑转率。电机输出扭矩的比值可以近似地看成两侧纵向载荷的比值,易知计算公式为:

(3)

通过分配系数K可以求得由质心侧偏所导致的分配扭矩公式为:

ΔT1=T(K-1)/(K+1)

(4)

其中,T为由加速踏板开度计算得出的原输出扭矩。

2 横摆角速度PI反馈调节

第1节描述了两侧驱动扭矩的初步分配方案。质心侧倾模块通过车辆侧倾角计算出分配扭矩,再加上由驾驶员踩踏板的开度所计算出的原输出扭矩,传输给控制器并用以控制两侧电机,这个控制过程是开环的,没有反馈调节的系统易在各环节误差及扰动的影响下出现偏差,准确性及稳定性均不理想。扭矩分配过小会导致转向性能不佳,而扭矩分配过大或者车速过快又容易造成甩尾。

针对此问题,本文设计了基于比例积分(proportion integration,PI)环节的横摆角速度控制模块。假设车辆是一个刚体,根据实际参数建立Ackermann-Jeantand模型,如图2所示。将车辆转向过程看作是绕瞬心的旋转运动,即可求得理想的过弯横摆角速度。

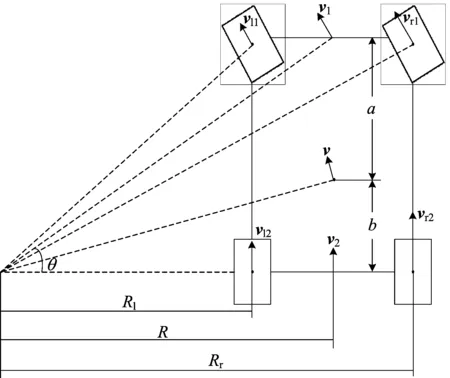
图2 Ackermann-Jeantand模型

由Ackermann-Jeantand几何模型可知,理想的瞬时横摆角速度计算公式为:

(5)

其中:ωl为左前轮角速度;ωr为右前轮角速度;ω为理想角速度;Rl为瞬心到左后轮的距离;Rr为瞬心到右后轮的距离;R为瞬心到后轴中心的距离。

左、右后轮作为驱动轮,因为打滑现象的存在会导致由后轮转速计算出来的车速与实际车速不等,因此采取前轮转速计算整车车速。

由上述方法得到理想过弯横摆角速度后,同实际横摆角速度共同作为横摆角速度控制器的输入量,进行PI控制调节。PI反馈控制的数学表达式为:

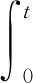
(6)

横摆角速度控制器模型如图3所示。

图3 横摆角速度控制器模型

3 电子差速算法仿真验证

3.1 电子差速模型搭建

本文采用Matlab/Simulink搭建整车动力学模型,并将基本参数设置为此赛车参数,具体见表1所列。

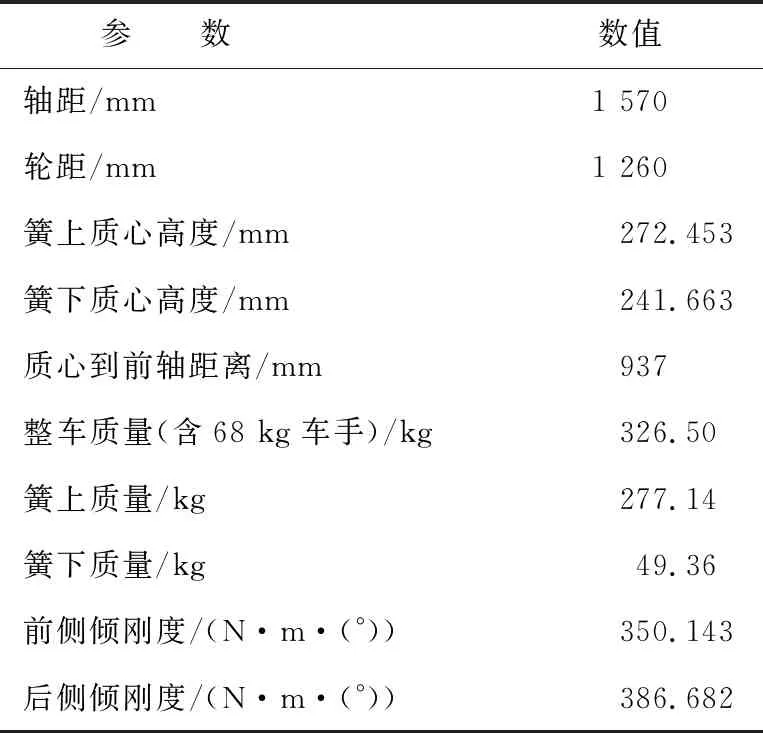
表1 车辆参数

依据上文公式及计算方法,再次使用Matlab/Simulink搭建电子差速控制模型,如图4所示。仿真模型中用信号输入模块模拟驾驶员操作车辆,输出一组方向盘转角和踏板开度信号,经质心偏移分配扭矩计算模块和横摆角速度控制模块计算后输出分配扭矩,在扭矩计算模块中,根据电机标定所得到的电机最大扭矩,将踏板开度线性转换为电机原扭矩后,再与分配扭矩和相加,经过限幅后输出给整车动力学模型,经计算后输出车辆的当前速度、质心偏移角及横摆角速度,并反馈到模型中形成闭环控制。

图4 电子差速控制模型

3.2 模型仿真结果及分析

3.2.1 直线行驶工况

保持方向盘转角为0°不变,加大踏板角度信号至75%并小幅波动,模拟车辆从静止开始直线加速。两侧电机驱动扭矩分配对比如图5所示。

图5 直线加速两侧电机扭矩

3.2.2 模拟过弯工况

直线加速后将踏板开度调小至0%,通过制动模块降低车速至30 km/h,再将踏板开度调节至30%,并将方向盘转角在0.2 s内线性增加至左侧45°,模拟车辆向左过弯状态(右侧过弯仿真结果与左侧过弯基本对称,本文不再列举)。

匀速过弯时两侧电机扭矩如图6所示,未加电子差速算法和加入电子差速算法时车辆横摆角速度的对比如图7所示。

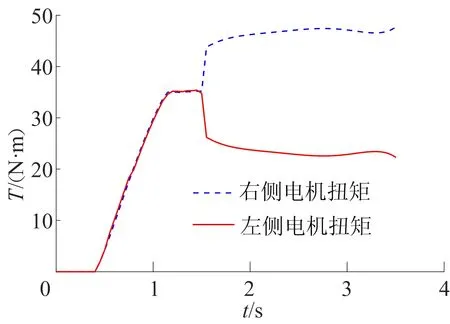
图6 匀速过弯时两侧电机扭矩

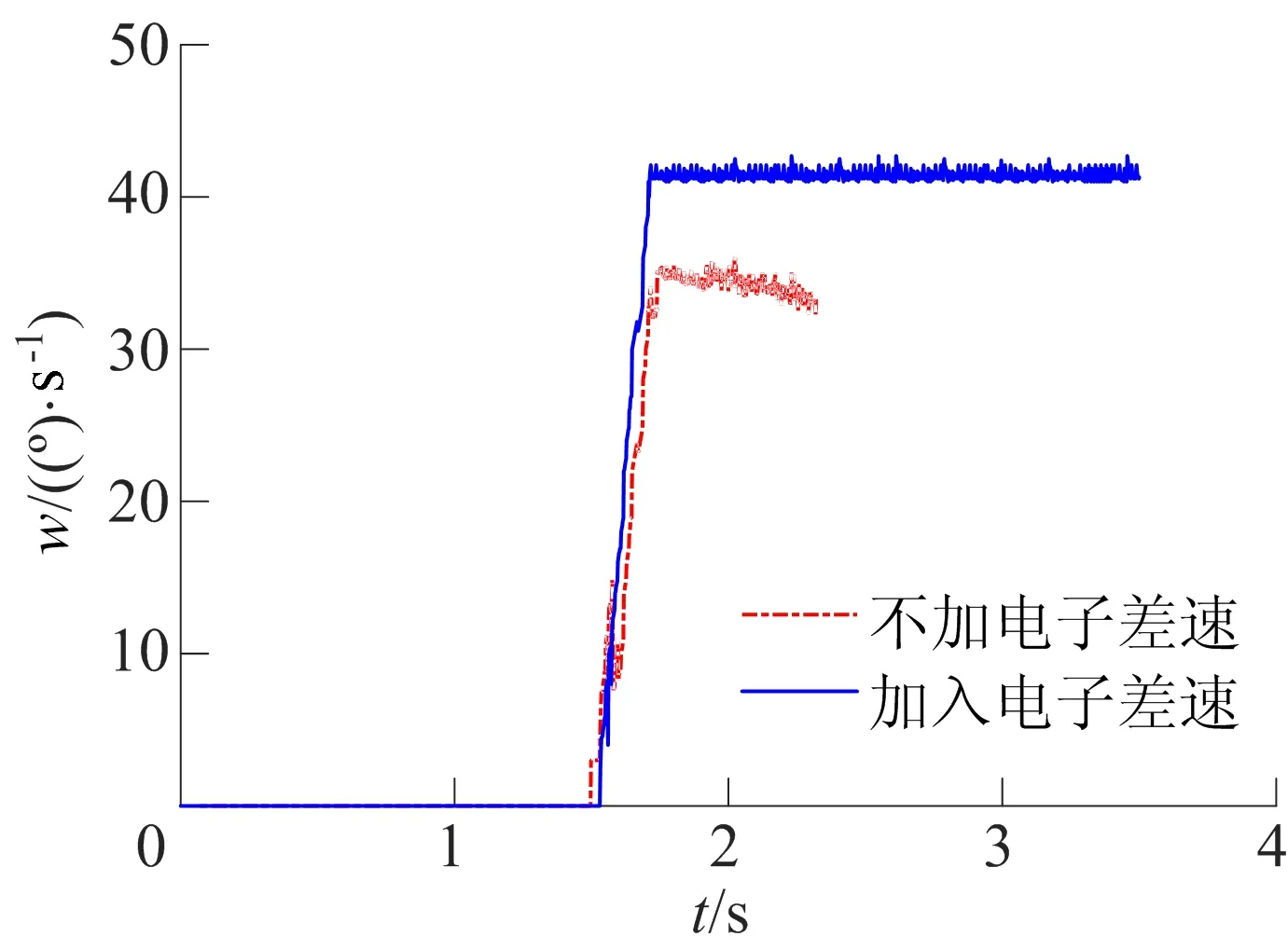
图7 车辆横摆角速度对比

3.2.3 仿真结果分析

由仿真结果可知,车辆直线加速过程中,两侧电机扭矩基本相等,电子差速算法不会对两侧电机扭矩分配产生影响。这保证了车辆在直线行驶中,电机的功率输出不会被限制。模拟过弯时,方向盘转角线性增大,车辆向左转弯并产生质心偏移及横摆角速度，电子差速算法开始工作并产生了20 N左右的分配扭矩,以横摆角速度为控制目标不断修正,从而得到一组相对稳定的横摆角速度。不加电子差速算法的试验组所得到的横摆角速度相对较小且不稳定；加入电子差速算法后,横摆角速度均值增加12.17 (°)/s,过弯速度提升39.13%。

以上结果说明,该电子差速算法可以在转弯过程中起到差速效果,增加了车辆转向时的响应速度及稳定性。

4 整车测试试验

为进一步验证本文所述电子差速算法的有效性和稳定性,在进行离线仿真之后,再利用实际车辆进行整车对比试验。车辆物理参数参考表1,试验车辆如图8所示。

图8 试验车辆

此赛车整车控制器使用Stm32系列单片机,在试验过程中,将电子差速算法加入控制程序,并将试验结果与未加差速算法的进行对比。车辆整车控制器(vehicle control unit,VCU)通过通用异步收发传输器(universal asynchronous receive/transmitter,UART)通信连接无线发送模块,向接收终端发送两侧驱动扭矩、横摆角速度等车辆实时数据,发送周期为10 ms。

在车辆机械、电气、电池箱等静态部分及制动性能、淋雨测试均满足安全性要求后,在天气晴朗、赛道干燥的情况下,选择综合性能测试场地进行试验。由车辆驾驶员驾驶习惯确定车辆过弯速度为30 km/h,并控制车辆由该速度进入直角测试弯道,重复试验3次,试验结果如图9所示。

由图9可知,本文电子差速算法在直线行驶时不会影响两侧电机的扭矩值,而在车辆转向过程中,会按照控制策略加大外侧电机扭矩并减小内侧电机扭矩值。该电子差速算法使车辆过弯时间减少约260 ms,过弯效率提升14%;并且算法的及时反馈使得车辆结束转弯状态后的反向横摆现象得以缓解,提高了车辆转向的快速性及稳定性。

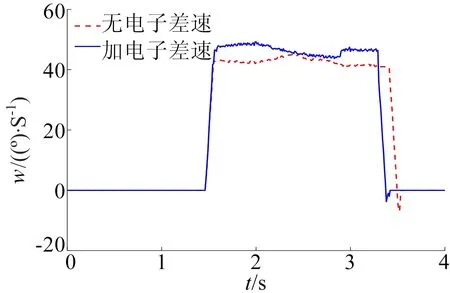
(b)图9 整车试验数据对比

5 结 论

本文针对自主设计的电动赛车提出了一种基于单片机控制的电子差速算法。以车辆质心偏移角度作为分配依据进行初步分配,横摆角速度作为PI环的反馈控制目标,对左、右侧驱动电机扭矩进行分配及修正。

仿真及试验结果表明,本文的理论分析正确,该电子差速算法有效地提高了车辆转向过程中的横摆角速度及其稳定性。