变转速工况下电动汽车涡旋压缩机切向泄漏研究
钱 月,唐景春
(合肥工业大学 汽车与交通工程学院,安徽 合肥 230009)
涡旋压缩机泄漏问题是阻碍其发展的主要不利因素之一,造成压缩机排气量减少、容积效率降低。在涡旋压缩机泄漏方面,国内外专家学者开展了大量的研究工作,提出了4种主要的切向泄漏建模方法:① 等熵流模型,将涡旋盘间隙简化为理想的收缩喷嘴,其中啮合间隙的切向泄漏可以看作是收缩喷嘴内部的流动过程[1];② 绝热可压缩黏性流模型(范诺流模型),也称为可压缩流体通过长、窄管道的摩擦流泄漏模型,一般假定流体没有与外界热交换,考虑了流体黏度对流体流量的影响[2-3];③ 不可压缩黏性流模型;④ 两相流泄漏模型。
文献[4]假设涡旋压缩机的间隙流动是不可压缩黏性流体的湍流流动,推导了间隙泄漏的流动方程,将轴向和径向间隙分别简化成极小的细缝通道和2个半径不同的圆之间的间隙,实验研究表明两结果吻合得很好。文献[5]建立了考虑动涡盘侧壁润滑膜厚度的两相流泄漏模型,提出一个反映涡圈壁上油膜厚度的润滑油黏附率参数,并通过实验与计算结果比较验证模型的正确性。近年来,文献[6-7]研究了涡旋压缩机止推轴承内、外表面因存在压力差导致的弹性变形而形成的楔形角,有助于止推面形成弹性流体润滑,并通过实验研究了不同压力差下止推面的润滑特性;文献[8]研究了由于动涡盘受到的倾覆力矩作用使轴向间隙形成楔形角引起的径向泄漏问题,建立楔形平板间气体泄漏模型,发现渐扩形泄漏通道对气体泄漏影响较大。
1 涡旋盘径向间隙润滑计算
在工作过程中,动涡旋盘绕着静涡旋盘转动,将该模型简化成径向滑动轴承数值模型进行径向间隙油的油膜润滑计算。其中静涡旋盘视作轴承,动涡旋盘视作轴颈,径向滑动轴承结构示意图如图1所示,动、静涡旋盘啮合示意图如图2所示。图1中:O、O1分别为轴承和轴颈的圆心;e为O、O1的距离,称为偏心距;ω为轴颈的角速度;h为轴承间隙中油膜厚度。膜厚计算公式为:
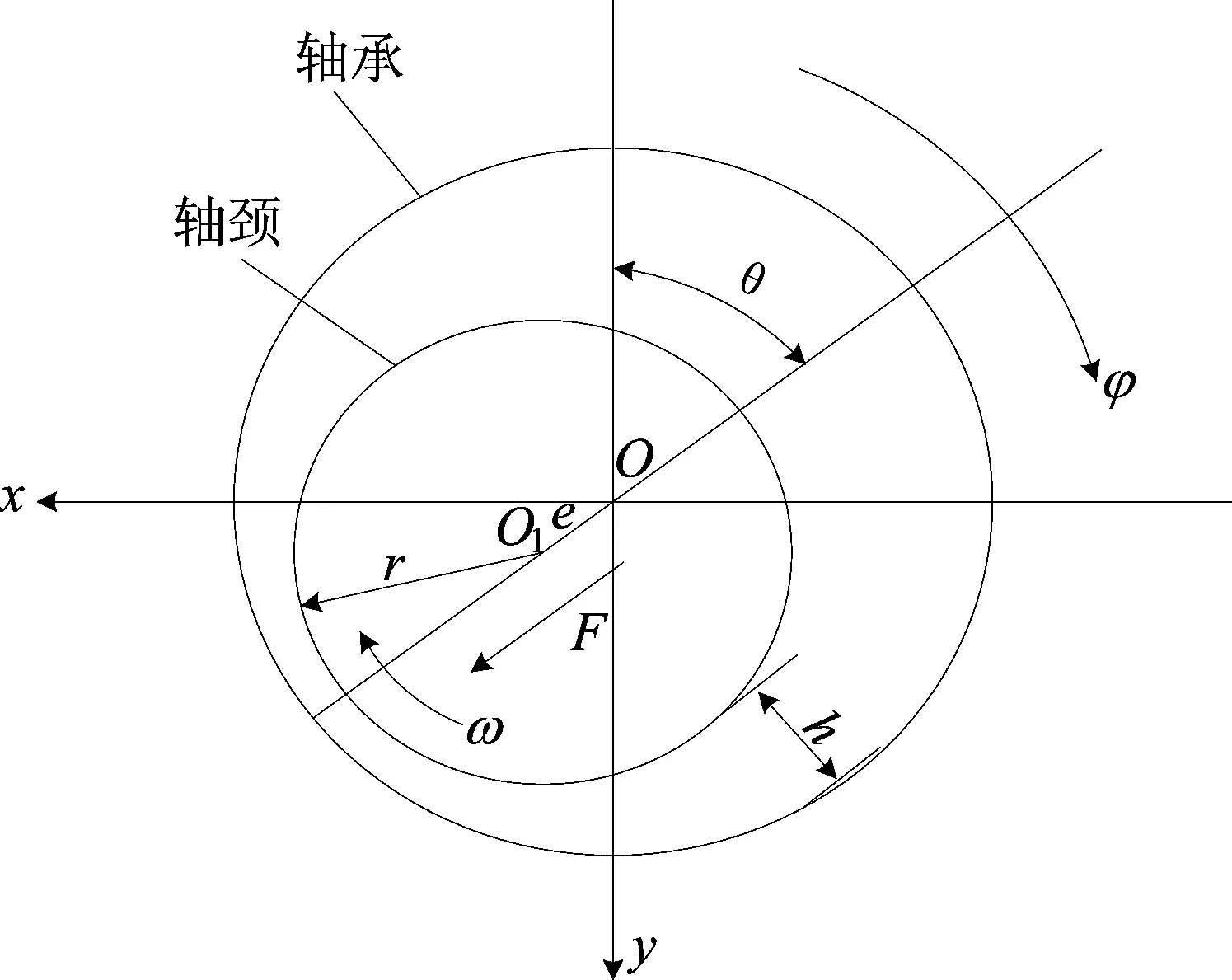
图1 径向滑动轴承结构示意图
h=C+ecosφ
(1)
其中:C为半径间隙,即轴承半径与轴径半径之差;φ为偏位角。
图2中:r、R分别为动、静盘在啮合点曲率半径;O、O1的距离为回转半径大小。在动、静盘啮合点M处的泄漏间隙上,根据润滑油油膜分布情况可以分析出M处油膜承载力。由于动、静涡旋盘的轮廓线是圆渐开线,因此在该点处的轴承、轴颈半径可由该点的曲率半径代替。
2 数值求解方法
2.1 雷诺方程求解方法
涡旋盘径向间隙的润滑分析采用雷诺方程[9],即
(2)
其中:h为油膜厚度;μ为润滑油工作温度下动力黏度;p为油膜压力;u为动涡旋盘线速度。
引入无量纲量φ=x/r,λ=z/(L/2),H=h/c,P=p/p0,并令p0=6uμR/c2代入(2)式,可得如下无量纲、极坐标形式的雷诺方程:
文化旅游部门数据显示,2017年全国乡村旅游人数达25亿人次,同比增长16%,约占国内游客的一半;消费规模超过1.4万亿元,同比增长27.3%,超过全国国内旅游收入的30%。文化和旅游部资源司副司长徐海军表示,乡村旅游已成为国内旅游消费主市场和投资新热点,且正在逐步与国际接轨。
(3)
其中:D为动盘直径;P为无量纲油膜压力;L为涡旋盘齿高。
采用有限差分方法,将径向间隙的油膜划分为m×n个方格,沿φ方向的列数用i编号,沿λ方向的行数用j编号,每个节点的位置用(i,j)二维编号表示。用各个节点上的压力值构成各阶差商,近似取代雷诺方程中的导数,且在数值求解过程中引入半步长差分法以提高计算精度,可以得到离散后的雷诺方程为:
(4)
将(4)式改写成如下形式:
Pi,j=
(5)
其中
Ei,j=Ai,j+Bi,j+Ci,j+Di,j;
由(5)式可将雷诺方程化为一组代数方程,利用数值计算方法,根据(i,j)节点周围4节点上的压力值来计算中间节点的压力值,由此解出各节点上的压力值,得到一组离散的压力数值,即可近似表达出油膜中的压力分布。根据这组压力值,用相应的数值积分方程求得油膜承载力、最大油膜压力、表面摩擦力等性能值。
对于有限长轴承,采用雷诺边界条件进行雷诺方程求解更接近实际情况,能较好地描述油膜压力分布情况。雷诺边界条件认为油膜不连续,具体的终止点在计算前不能被人为预测,应该根据油膜破裂条件计算得到,压力油膜的终点在最小油膜厚度后油楔发散区的某个位置处。本文采用雷诺边界条件进行求解。
2.2 油膜承载力
油膜承载力(油膜反力)F为:
(6)
(7)
(8)
其中,Fx、Fz分别为F在x、z轴方向的分量。
2.3 表面摩擦力计算
压缩机运动过程中曲轴转动引起的涡旋盘表面摩擦力为:
(9)
(10)
其中,Fu、Fv分别为动、静涡旋盘表面摩擦力。
2.4 润滑油黏温方程
用于制冷剂R-134a的润滑剂是一种合成润滑油,一般为聚烷基乙二醇(PAG),其黏度-温度方程[10]为:
μ=exp[-12.995+3 124.094/(t+273.15)]
(11)
3 结果与分析
选取排量为28 cm3的涡旋压缩机,进行在主轴转角变化的4个时刻(主轴转角θ为0°、90°、180°、270°)时动、静涡旋盘啮合点油膜的润滑计算。
4个时刻的动、静涡旋盘啮合示意图如图3所示,主轴转角为90°时啮合点A的计算工况参数见表1所列。
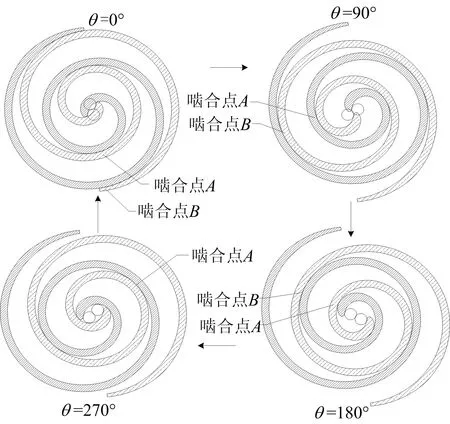
图3 主轴转角变化4个时刻的动、静涡旋盘啮合位置示意图
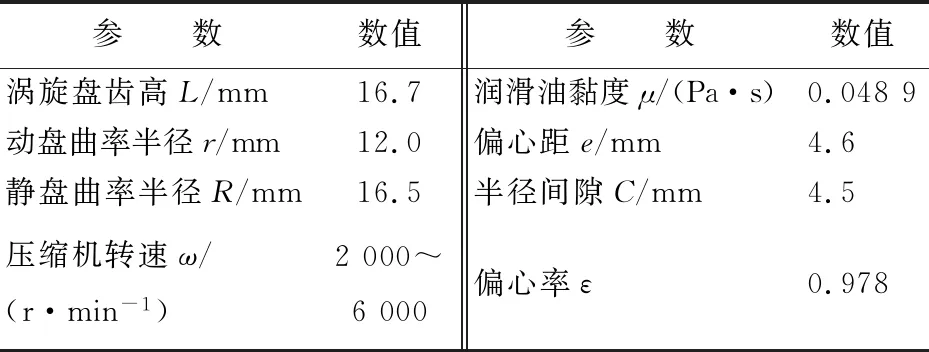
表1 主轴转角为90°时啮合点A的计算参数
径向间隙上的无量纲油膜压力的三维分布如图4所示,近似为连续的抛物面。
从图4可以看出:在收敛油楔区域内,油膜压力逐渐上升;在最小油膜厚度处,油膜压力达到最大值;随后润滑油进入扩散区,油压急剧下降,并在某一转角处油膜破裂。

图4 油膜压力的三维分布示意图
最大油膜压力随压缩机转速变化的分布规律如图5所示。
从图5可以看出:最大油膜压力值随着压缩机转速增加而增大,压缩机转速越大,径向间隙越小;在主轴转角为180°左右时,最大油膜压力值最大,由于此时压缩腔体积较小,油膜压力增大且间隙较小,压缩效率高。
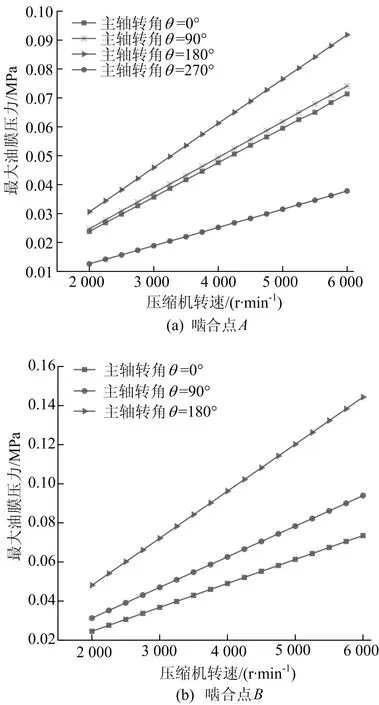
图5 最大油膜压力随压缩机转速变化的分布规律
表面摩擦力随压缩机转速变化的分布规律如图6所示。

图6 表面摩擦力随压缩机转速变化的分布规律
当压缩机转速增大时,动静涡旋盘表面摩擦力会随之增大,从而增加涡旋盘表面磨损,引起压缩机功耗增加。
4 实验验证
考虑到涡旋压缩机工作腔内部润滑油压力及油膜厚度的测量难度,本文试验方案采用排量为28 cm3的涡旋压缩机进行性能试验,测试在不同转速(3 000~6 000 r/min)下的制冷剂流量及压缩机耗功,由制冷剂流量计算得出制冷量进而计算出性能系数COP值。试验方法采用第二制冷剂量热器法,试验系统如图7所示。
图7中:a为压缩机;b为冷凝器;c为节流阀;d为蒸发器盘管;e为电加热器;f为量热器;g为第二制冷剂压力表;h为压缩机吸气压力表;i为压缩机排气压力表。
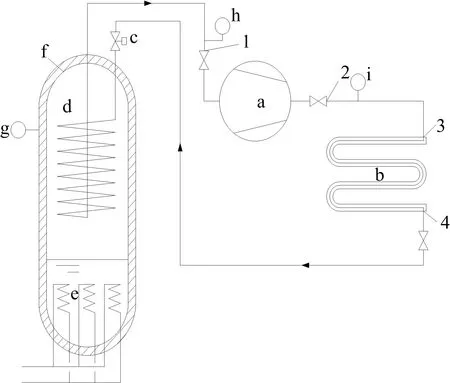
图7 制冷压缩机性能试验装置系统
压缩机吸气压力由节流阀调节,吸气温度由电加热量调节,排气压力通过改变冷凝器冷却水量调节。关闭量热器制冷剂进、出口截止阀得出量热器热损失系数为:
(12)
其中:Φh为电加热输入功率;tb为第二制冷剂稳定压力的饱和温度;ta为平均环境温度。制冷剂流量计算公式为:
(13)
其中:Φi为输入量热器的热量;ts为第二制冷剂饱和温度;h3、h4分别为冷凝器制冷剂进、出口蒸汽的比焓,单位kJ/kg。
试验工况参数为:压缩机吸气温度10.66 ℃,吸气压力299.945 kPa,排气压力1 500.001 kPa,蒸发温度0.66 ℃,冷凝温度55.25 ℃,过热度10 ℃,过冷度5 ℃。绘制出转速与压缩机耗功及能效系数COP的关系曲线,如图8所示。由图8可知,随着压缩机转速的增大,制冷量增加,但是压缩机运行功耗也相应增加;在压缩机转速达到5 000 r/min时,性能系数COP达到最大值2。
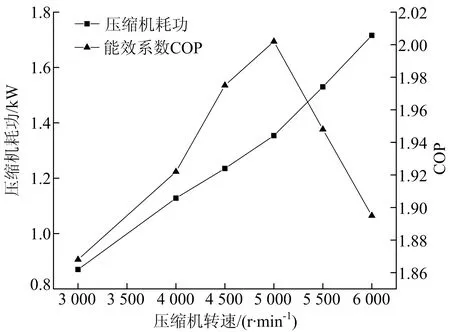
图8 最大油膜压力随压缩机转速变化的曲线
5 结 论
(1) 无量纲油膜压力的三维分布近似为连续的抛物面。在最小油膜厚度处,油膜压力达到最大值。
(2) 最大油膜压力值随着压缩机转速增加而增大,即压缩机转速越大,径向间隙越小,但动、静涡旋盘表面摩擦力会随之增大。主轴转角为180°时,泄漏间隙较小,压缩效率高。
(3) 随着压缩机转速的增大,径向间隙减小,制冷剂流量增大,制冷量增大,同时压缩机运行功耗也相应增加,转速达到5 000 r/min时,其性能系数COP达到最大值2。因此,为了减小间隙泄漏的影响,同时避免造成摩擦损失,最佳转速为5 000 r/min。

