可重构的微分方程通用解算器研究和实现

张多利,魏 可,胡永阳,聂言硕,侯 宁,宋宇鲲

(1.合肥工业大学 电子科学与应用物理学院,安徽 合肥 230601; 2.教育部IC设计网上合作研究中心,安徽 合肥 230601; 3.河南城建学院 电气与控制工程学院,河南 平顶山 467041)

常微分方程(ordinary differential equation,ODE)是对世界认知的一种基础数学方法。常微分方程的初值问题(initial-value problem)在满足李普希茨(Lipschitz)条件时存在唯一的连续可微解[1],因为其精确解析解难以获得,所以通常使用数值方法计算求解。在实时检测宏观和微观事物、自然现象、运动规律和连续变化过程的工程应用中,为高效求解需求量大、运算量大、精度要求高的ODEs,往往需要采用硬件代替通用处理器实现。

四阶龙格-库塔法(fourth-order Runge-Kutta,RK4)是一类高精度迭代法,常用于非刚性ODE数值解。目前,基于现场可编程逻辑门阵列(field programmable gatearray, FPGA)的RK4微分方程数值解算实现已得到广泛应用[2-3]。文献[4-5]介绍了实时求解洛伦兹系统的FPGA实现,分别应用于数据流加密和混沌动力系统计算中;文献[6-7]采用RK4结构在FPGA上分别实现了风力涡轮机和感应电机的动态仿真;文献[8]介绍了系数可配置的卫星飞轮RK4动力模型,并在FPGA完成了硬件实现;文献[9-13]在不同的微弱信号检测应用中实现了Duffing微分方程RK4的FPGA实现;文献[14]完成了使用RK4求解弹道方程的FPGA实现;文献[15]介绍了在FPGA中采用RK4求解医学领域PK/PD模型。

上述研究均针对确定ODE展开,其求解电路结构的通用性考虑不足。其中,对于RK4计算结构,文献[4]采用计算全展开结构以获得高性能;文献[5-7]采用迭代复用结构,减少了所需电路面积。对于ODE计算结构,文献[9,12-13]采用非流水线结构,在同一时间内只能完成单个ODE求解;文献[10]采用流水线结构,大批量数据处理速度优势。对于ODE求解灵活性方面,文献[12-13]通过多次求解得到不同系数条件下的求解结果;文献[8]给出的求解方程可改变相关系数数值,能够完成不同系数条件下的方程求解。

综上所述,为了满足各种应用对ODEs求解的灵活性、高效性、实时性等多方面的需求,本文设计了一种高性能通用可重构微分方程解算器(reconfigurable differential equation solver,RDES),RDES的主要特征如下:

(1) 采用可重构的原理,支持在线重构完成不同结构、阶数、变量等条件的ODEs求解任务,增加系统通用性。

(2) 可根据需要重构为流水线或循环迭代结构完成RK4计算流程,有效满足不同求解收敛速度的要求。

(3) 确定ODEs下,支持不同初始条件下的批量求解,显著提高初始值、系数等因素的收敛速度。

1 系统架构设计

1.1 RK4算法原理

RK4是由欧拉方法改进得到的一种在工程上应用广泛的高精度ODE数值解法,可求解一阶微分方程或微分方程组。对于包含多个变量的ODE,对应的RK4求解公式为:

(1)

(2)

其中,h为步长。对于变量x,4组Kx值对应的表达式为:

(3)

y、z等变量表达式与(3)式相似。

1.2 系统架构

RDES架构和系统工作流程如图1所示。RDES基于可重构方法实现,整体架构包括RK模块、可重构计算阵列(reconfigurable computing array,RCA)模块、迭代循环控制(iterative loop controller,ILC)模块、配置信息和变量数据存储器(memory)及与外界交互信息的接口(interface)。

由图1b可知,通过编译工具整理待求解ODE的结构,合并分支,确定其包含的基础算子。将整体计算结构拆解为由基本运算单元组成的单步或连续计算。基本运算单元为RCA包含的加、减、比较和选择、乘、除、开方、三角函数计算等。通过映射工具将拆解出的各组运算映射到RCA中,并生成相应的配置信息。完成后RDES就能开始工作。

图1 RDES架构和系统工作流程

在RDES的工作流程中,通过interface写入配置信息和变量数据信息,存储到memory中,变量数据可以是大量不同初值条件ODEs的变量信息。首先取出配置信息对RCA进行配置,配置完成后开始ODE求解计算。对应(2)式计算流程,从memory中逐个取出各ODE的变量数据x0,y0,…,z0,输入RK模块,经RCA计算得到新一组变量x1,y1,…,z1。不满足停止计算条件的变量数据写回memory,作为下一组变量数据输入RK模块计算。由此迭代循环直到输入系统的所有ODEs都满足条件,批量求解完成。系统的数据交互、迭代循环计算流程都由ILC控制实现。

1.2.1 RK模块

RK模块结构如图2所示,该模块是按Runge-Kutta计算流程设计的系统核心计算模块,主要由RCA模块、f(Ki)运算模块、斜率生成(slope generator)模块组成。RCA模块根据输入的变量值计算各个变量的Ki值;f(Ki)运算模块根据需要对已获得的K值进行处理;斜率生成根据所有RCA输出的K值计算变化斜率,进而得到输出结果。

图2 RK模块结构

RK模块可实现任意阶数的Runge-Kutta计算。本文已完成的RK模块取i值为4,适用于四阶以内的Runge-Kutta计算。以RK4为例,计算步骤由(2)式、(3)式得到,即输入变量初值x0,y0,…,z0逐次经过4个RCA模块得到K1～K4的值,3个f(Ki)运算模块分别计算K1h/2、K2h/2、K3h的值,斜率生成计算(K1+2K2+2K3+K4)h/6,最后与初值求和,得到输出新值x1,y1,…,z1。

1.2.2 RCA模块

RCA是RDES的基本计算模块,是由每行4个处理单元(processor elements,PE)形成的固定互连结构与行间数据传输网(data transmission network,DTN)交替排布组成的阵列,模块结构如图3所示。通过重构实现不同ODEs的计算结构,即(1)式所有输入变量到输出变量一阶导数值的数据路径。

图3 RCA模块结构

本文已完成的RCA结构行数为5行,适用于包含4个以内变量数的ODEs。能够实现同行相邻PE的数据交互,行间数据经DTN的单向传递,能够处理ODE中的计算分支、变化系数、变量复制等情况。对于超过4变量或超过单个RCA结构允许计算量的ODEs,可通过多次重构计算。

RCA模块中3种PE为固定互连关系的不同运算实现:① 比较选择计算单元,如图3中PE1,包含浮点比较器和选择器,可以处理ODE计算中的分支情况;② 乘加计算单元,如图3中PE2,包含浮点乘法器和加减法器,实现最常用的乘法和加减法计算;③ 复杂计算单元,如图3中PE3包含浮点除法器、开方器、CORDIC计算单元,主要实现三角函数和多种超越函数的计算。

RCA模块主要由控制路径和数据路径2个部分组成。外层RK模块通过控制路径写入配置信息,广播到所有PE和DTN进行配置。配置完成后,RCA模块形成从变量输入到K值输出的完整数据路径,即可根据输入变量值计算得到对应K值,输出至RK模块。

1.2.3 ILC模块

ILC模块负责RDES系统从信息配置、数据输入到迭代循环停止的完整流程的控制。ILC模块控制配置信息和变量数据的接收。检测到配置完成信号后,控制取出初始变量数据x0,y0,…,z0,写入RK模块计算。RK模块计算输出x1,y1,…,z1。ILC模块在数据计算输出后,根据停止迭代信号iteration-finish的值判断下一步操作。若信号值为0,则保留该组数据,作为新的输入变量数据作下一轮迭代计算;若信号值为1,则ODE结束计算,该组数据不再存储。ILC模块对结束计算的ODE计数,finish-num计数到输入的N个方程都结束则完成计算任务。ILC模块控制所有变量遵循同样的迭代循环流程,其中对变量x的迭代循环控制过程的伪代码如下:

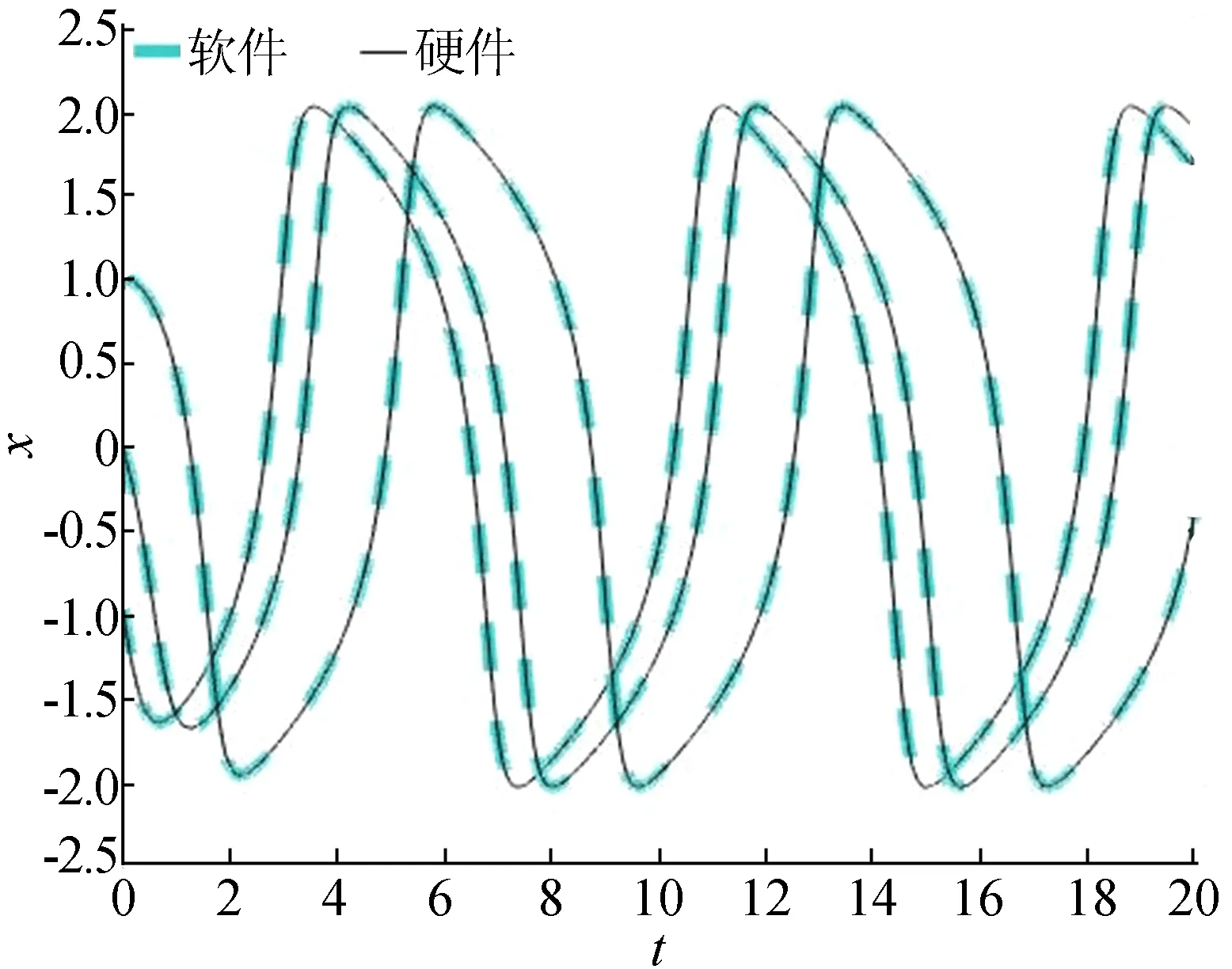
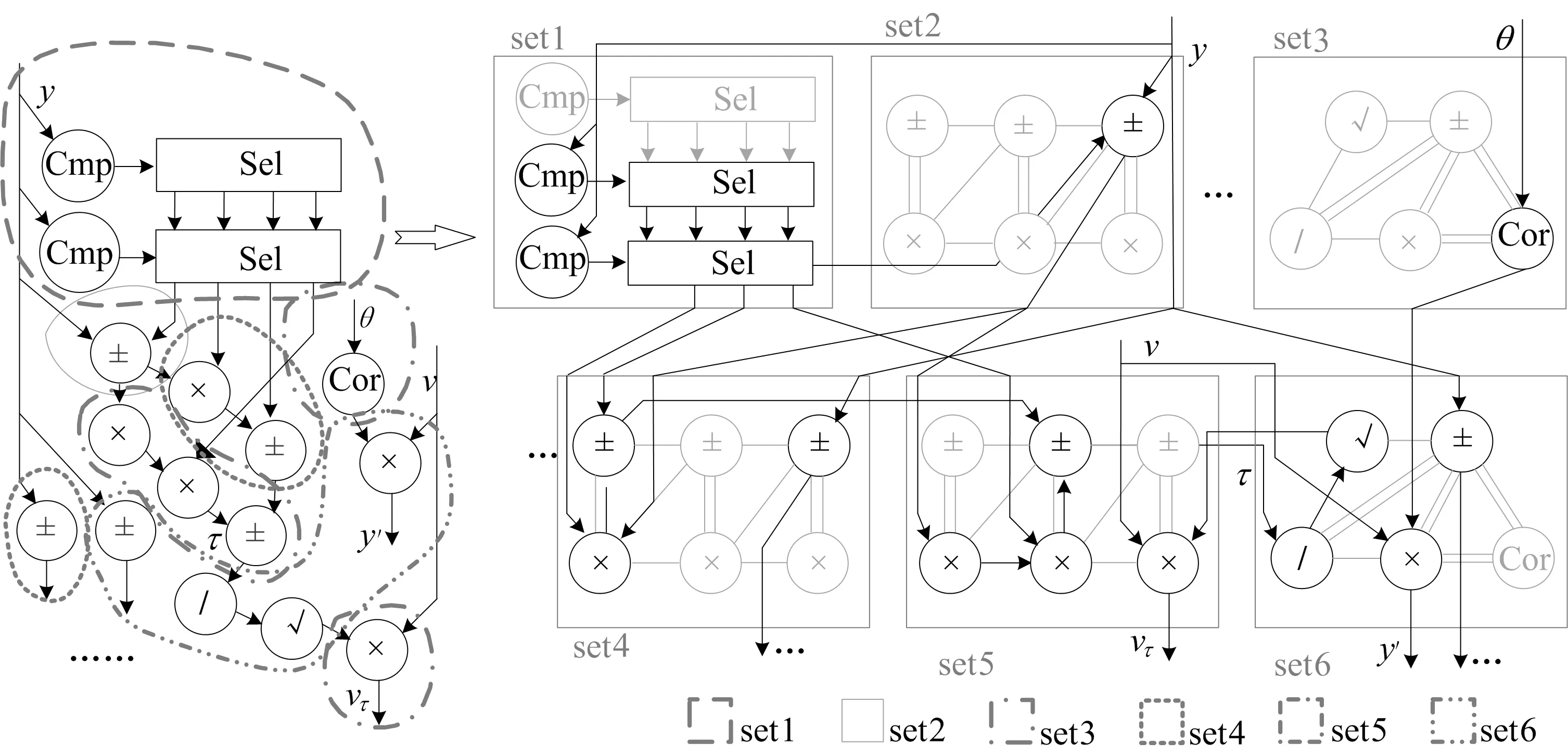
while finish-num

if configuration done then

if iteration-time==0 then

x←x0;

data valid sign is decided by input data

valid sign.

else

x←x1;

if iteration is not done then

data valid sign is decided by iteration data valid sign.

else

data valid sign is set to 0;

finish-num←finish-num+1;

end while

通过配置信息可以得到停止迭代条件,设计支持包括迭代次数限制、停止时间限制、变量数值达标等多种条件,满足实际应用中不同ODEs的需求。ILC模块在每轮迭代后作相应的条件判断,结果写入iteration-finish信号,以完成对变量数据的控制。

2 应用映射与实验分析

软件实现在Intel(R) Core(TM) i7-4790 CPU@ 3.60 GHz,32 GiB内存、64位操作系统的PC机上,使用Microsoft Visual Studio 2017软件的x86编译环境,用C++语言作为编程工具,设定数据格式为双精度浮点数;硬件实现采用Xilinx Vivado 2018.3作为编译工具,并在Virtex-7 XC7V2000TFLG上实现整个设计,设定数据格式为单精度浮点数。使用Matlab软件完成计算数据图像绘制,并对比软硬件执行时间。

2.1 范德波(Van der Pol)方程

Van der Pol方程是描述振荡的一种基础模型。其往复的周期运动易受扰动影响,且对初值变化敏感。因此实际研究时往往需要实时求解。方程常用形式为:

x″+μ(x2-1)x′+x=0

(4)

其中,μ为可变的阻尼系数。

将方程转化为一阶微分方程组。设y=x′,则有:

(5)

2.1.1 方程映射

该方程计算数据流图(data flow graph,DFG)及其在图3 RCA中的映射结构如图4所示。

DFG通过拆解分组(set),映射到RCA的PE中,形成图4的计算路径,并作为配置信息存储下来。这里1个Van der Pol方程使用了2个PE2完成映射。

2.1.2 实验与结果分析

实验100组不同初值或系数条件的Van der Pol方程求解。分别在PC和FPGA板上完成计算。

硬件实现结果能够满足Van der Pol方程实时求解的需求,其中使用Matlab软件作出的随机选取的几组FPGA实测结果和软件结果的对比图像如图5所示。软硬件计算结果最大绝对误差为2.043×10-4,因此软硬件计算结果可视为一致,不同初始条件下的方程可能求解出不同的振荡关系,据此可使初始值、系数条件的选择范围快速收敛。Van der Pol方程实验软硬件实现时间对比见表1所列。由表1可知,硬件实现相对于软件实现约有16.93倍的加速比。

图5 几组Van der Pol方程软硬件对比图像

表1 软硬件计算Van der Pol方程时间比较

2.2 阿波罗(Apollo)卫星运动轨迹方程

人造卫星的运动轨迹与三体引力、太阳光压、当前位置和速度、调整轨道的推力等多方面因素有关。因其复杂多变的干扰因素,对批量求解卫星在不同条件下的运动轨迹就有了需求。采用简化的Apollo卫星运动轨迹方程作为测试例,求解不同初值条件下Apollo卫星运动轨迹和状态。卫星运动轨迹(x,y)满足:

(6)

其中:μ为变化系数;λ=1-μ。

将方程转化为一阶微分方程组。设x1=x′,y1=y′,则有:

(7)

实验150组不同初值或系数条件的Apollo运动方程求解。硬件实现结果能够满足Apollo方程批量求解的需求,其中随机选取的几组FPGA实测结果和软件结果的对比轨迹图像如图6所示。

图6 几组Apollo运动轨迹软硬件对比图像

软硬件计算结构最大绝对误差为6.524×10-4,因此软硬件计算结果可视为一致,不同初始条件下的方程求解可能产生不同的运动轨迹,据此可对满足需求的初始条件快速筛选,从而实现快速收敛。

Apollo运动方程实验软硬件实现时间对比见表2所列,由表2可知，硬件实现相对于软件实现约有112.64倍的加速比。

表2 软硬件计算Apollo方程时间比较

2.3 炮弹弹道方程

炮弹的飞行轨迹受大气状况、初始条件、炮弹自身性质等多方面因素影响。为在当前大气条件下精准击中目标点,需要大批量求解炮弹发射初始条件、变化系数条件有细微调整的弹道方程，因此批量快速求解弹道方程就有重要的意义。简化弹道方程模型为包含速度v、飞行方向与水平面的夹角θ、当前位置距离发射点的垂直距离y、当前位置距离发射点的水平距离x4个变量,微分方程组表达式[16-17]为:

v′=-cH(y)F(Vτ)-gsinθ,

y′=vsinθ,

x′=vcosθ

(8)

其中:c为弹形系数;g为重力加速度,是变化系数;H(y)为空气密度函数;F(Vτ)为阻力系数，是中间变量[18]。

2.3.1 方程映射

在弹道方程计算流程中,变量v的K值求解流程较复杂,需要求解出6个中间变量,包括虚拟温度τ、空气密度函数H(y)、虚拟速度vτ、阻力系数F(Vτ)。将方程中求解τ和F(Vτ)的条件分支结构通过比较和选择操作合并计算后,得到弹道方程的部分DFG及对应映射图像如图7所示。

图7 弹道方程计算部分DFG和映射图

2.3.2 实验与结果分析

实验200组不同初值或系数条件的炮弹弹道方程求解。硬件实现结果能够满足弹道方程批量求解的需求,其中随机选取的几组FPGA实测结果和软件结果的对比弹道图像如图8所示。

图8 几组弹道软硬件对比图像

软硬件计算结构最大绝对误差为1.482×10-6,因此软硬件计算结果可视为一致,不同初始条件下的炮弹能够产生不同的飞行轨迹,产生不同的落点,据此可对靠近目标落点的初始条件快速筛选,从而实现快速收敛。炮弹弹道方程实验软硬件实现时间对比见表3所列,硬件实现相对于软件实现约有45.23倍的加速比。

表3 软硬件计算弹道方程时间比较

3 结 论

本文提出了一种可重构的微分方程通用解算器RDES,能够重构完成不同结构、阶数、变量等条件的ODEs求解任务,拓展了系统通用性。几组实际应用的微分方程验证实验结果表明,RDES在完成不同初始条件的ODEs批量求解计算时较通用处理器具有很大的速度优势。