光伏逆变器散热系统气动噪声分析研究
张 磊,郑昌军,张小正
(1.合肥工业大学 机械工程学院,安徽 合肥 230009; 2.合肥工业大学 噪声振动工程研究所,安徽 合肥 230009)
0 引 言
近年来,随着能源消耗和环境保护问题受到大众的广泛关注,我国家用太阳能光伏发电产业呈现快速发展的趋势,其中光伏逆变器作为该产业中的重要装备,在解决自身散热问题的同时,还需要考虑散热系统带来的气动噪声问题。光伏逆变器散热系统中主要的气动噪声源是轴流风扇,因此有必要对轴流风扇的流场特性和声场特性进行分析和研究。
随着数值计算的发展,在解决产品低噪声设计问题时可以使用数值仿真的方法对产品的噪声进行预测,进而为整个设计阶段的噪声水平评估与控制提供可靠的参考和指导。在实际工程中,针对空调、冰箱及其他含有轴流风扇的电器,大多采用Fluent、STAT-CCM+、LMS.Virtual.lab等软件对轴流风扇气动噪声水平进行数值仿真预测。文献[1]使用Fluent软件中的WMLES(wall-modelled large eddy simulation)模型对轴流风扇的流场特性进行了分析,并计算得到了叶片上的非定常力,然后使用FW-H(Ffowcs Williams-Hawkings)声类比模型计算出自由场内的声压级;与实验测试得到的结果进行比较之后发现,声场在指向性上有较好的一致性,但在噪声水平上存在差异,其主要原因是没有考虑风扇机壳对声场的影响。文献[2]使用Fluent软件对船泵冷却轴流风扇进行了声场特性分析,发现轴流风扇叶片形状会对气动噪声产生影响,但该研究的声压级预测结果与实验数据有近6 dB的误差。文献[3]将分体式空调机作为研究对象,使用Fluent软件中的FW-H声类比模型对不同叶片参数下风扇的流场特性和声场特性进行了分析和比较,并在此基础上提出了相应的叶片优化设计方法。国内研究者对轴流风扇产生的气动噪声也做了相应研究。文献[4]将单独的小型轴流风扇作为研究对象,使用Fluent中的RNGk-ε模型对风扇流动特性进行了分析,指出叶尖会产生涡流,叶尖涡撞击相邻叶片表面会对气动噪声产生较大的影响;但没有使用声场仿真对气动噪声的辐射水平进行相应分析。文献[5]使用Fluent中的大涡模拟(large eddy simulation,LES)和FW-H声类比模型对轴流风扇气动噪声进行了数值模拟,结果表明叶片尾缘涡脱落产生宽频噪声,叶尖涡产生离散噪声,声场结果表明仿真计算的基频与理论计算的基频相符。文献[6]使用Fluent软件中的LES模型和FW-H声类比模型对3种不同叶片类型轴流风扇的流场特性和声场特性进行了研究,发现后掠风扇的远场声压级比其他类型风扇下降了1.1 dB;但风扇基频处仿真数值与实验数值存在一定误差,误差达10%。文献[7]使用Fluent软件的FW-H声类比模型对风机蜗舌和蜗壳的噪声水平进行了仿真计算,并对室内机流道结构参数进行了优化;但发现噪声仿真数值与实验数值存在一定误差,原因是FW-H模型是针对自由空间的声传播提出的,实际模型则是在非自由场中,噪声源会受到机壳的影响,因此气动噪声预测结果会存在较大误差。
现有的文献大多使用Fluent对单个独立风扇产生的气动噪声进行数值仿真,而忽略了周围结构对声场计算的影响,因此在风扇周围结构较为复杂时,该类方法会产生较大的数值仿真误差。此外,目前国内外对光伏逆变器散热系统噪声水平的数值仿真研究仍较少。
针对上述问题,本文采用混合仿真的方法,将光伏逆变器散热系统结构对风扇的影响考虑在内,进行流场和声场分析,并对进气格栅进行结构改进,以降低光伏逆变器散热系统的噪声水平。
1 流体力学数值计算
1.1 几何模型简化和网格划分
光伏逆变器主要用于直流电与交流电变换装置,也可用于交流供电设备。逆变器散热系统主要采用2个小型轴流风扇进行散热。轴流风扇主要参数为:叶片7个,风扇外径56 mm,叶顶间隙3 mm,转速9 000 r/min。
逆变器初始模型较为复杂,如图1a所示。为了便于模型划分网格和提高网格质量,需要对初始模型进行简化,主要是去除螺栓孔、线缆孔、流道内的倒角等细小部分,简化后的逆变器模型如图1b所示。
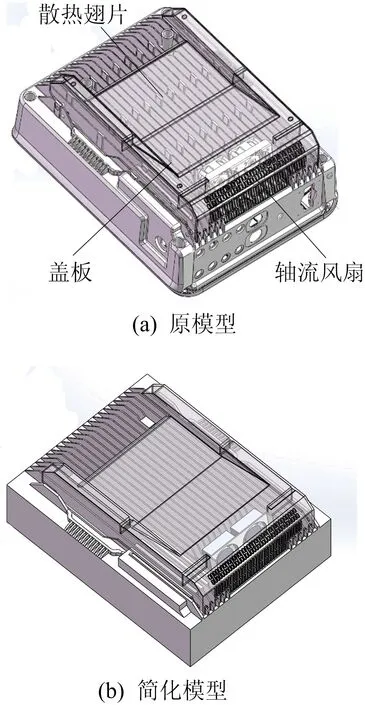
图1 逆变器模型
在实际工况中,为了模拟真实情况,将逆变器散热系统的入风口区域和出风口区域进行延长,同时将2个轴流风扇分别使用2个旋转域包络在内,从而将流体域划分为静止域和旋转域,如图2所示。

图2 计算区域划分
使用HyperMesh划分网格。由于散热系统和风扇周围的结构复杂,采用非结构化四面体网格进行划分,同时为了很好地捕捉压力梯度和流场特性,在风扇周围的旋转区域和风扇架附近进行网格加密处理,近壁面使用壁面函数进行处理。划分后网格总数为1.074 42×107,检查网格质量达到要求后导入Fluent中进行流场计算。
1.2 边界条件设置
在流体数值计算方法中要让物理问题有唯一解,必须要指定边界上的物理量。由于整个模型在开式空间内,为了能够较好地模拟实际情况,将除地面以外的其他面作为压力边界,从中间划分为2个不同的压力边界,一侧是压力入口边界,另一侧是压力出口边界。由于边界距离风扇有较远的距离,因此压力入口边界和压力出口边界可以视为常压条件,静压设置为大气压力。风扇叶片壁面设置为旋转壁面条件,设置壁面相对速度为0,其他边界使用无滑移壁面边界条件。风扇的旋转域使用多重参考系(multiple reference frame,MRF)来模拟风扇的旋转,设置旋转域转速为9 000 r/min,静止域和流动域之间使用interface进行关联。
1.3 物理模型和计算方法选择
物理模型的选择会对流场结果的准确性有较大的影响。因为选择标准k-ε模型在强旋流或者带有弯曲壁面流动时有可能会出现一定的失真[8],另外考虑到散热系统流道较为复杂,所以选择使用RNGk-ε模型。该模型是对标准k-ε模型的修正,主要是对湍流耗散率方程进行修正,以提高强应变流动的模拟精度。具体的流动控制方程[8]如下:
(1)
(2)
(3)
(4)
其中:ρ为流体密度;t为时间;xi为空间坐标;k为湍动能;ε为湍流耗散率;ui为时均速度;μeff=μ+μt,μt=ρCμk2/ε,μ为流体动力黏度;Gk为由于平均速度梯度引起的湍动能的产生项;R为用重整化群方法推导的函数项;C1ε、C2ε、C3ε、η0、β、Cμ为常系数;αk、αε分别为湍动能k和耗散率ε的有效湍流普朗特数的倒数;Eij为时均应变率。
首先进行定常计算,求解器使用SIMPLEC算法,使用默认的收敛因子,当各项残差趋于稳定,且进出口的质量流保持在0.046 2 kg/s,即视为收敛;然后进行非定常计算,计算时使用非稳态雷诺平均模型,设置时间步长为1×10-5s,时间步数为800。
1.4 流场特性分析
在对流场特性进行分析时,考虑到2个风扇结构相同,周围流道环境相似,使得2个风扇叶片内部流场特性相似,因此下面只选择其中一个风扇进行举例分析。根据现有研究发现,叶尖涡产生的非定常脉动载荷是产生风扇离散噪声的主要原因[5],因此在风扇的轴向方向做截图,具体截面位置如图3所示,绘制出流线图和静压云图。

图3 截面位置
风扇叶片尖漩涡位置如图4所示。从图4a可以看出,相邻叶片之间存在较大的压差,导致气流在叶片间产生较强的对流,从而在叶片中间位置形成漩涡。对比图4a与图4b可以看出,漩涡中心朝向吸力面移动;而从图4d可以看出,漩涡完全消失。

图4 风扇叶片尖漩涡位置
因为漩涡会使得叶片表面产生较大的压力脉动,通过观察不同的截面图,发现漩涡主要出现在叶片前缘的叶尖附近,所以可以推断靠近前缘位置的叶片表面压力脉动较大。
为了更好地说明叶片表面压力脉动和漩涡有较大的关系,绘制相同风扇叶片表面的静压云图,如图5所示。
图5a中,叶片前缘位置A压力偏差较大,负压接近120 Pa,对应在声压级云图5c中,位置C的声压级明显大于其他位置;同样,在整个叶片表面B位置的压力偏差也较大,相应的声压级云图中,位置D的声压级比周围区域大。图5b中,吸力面负压最大的位置靠近叶片前缘的位置E,最大负压达到220 Pa;对比声压级云图5d中,声压级最大的位置是靠近叶片前缘的F区域,并沿着风扇叶片表面的顺时针方向逐渐变小。通过对比静压分布和声源面声压级分布,证明了声源表面声压级受到压力脉动的影响,压力脉动量大,相应声源表面的声压级也会增大。

图5 风扇叶片云图分析
选择风扇轴线方向流道内静压云图进行分析,流道内截面静压云图如图6所示。
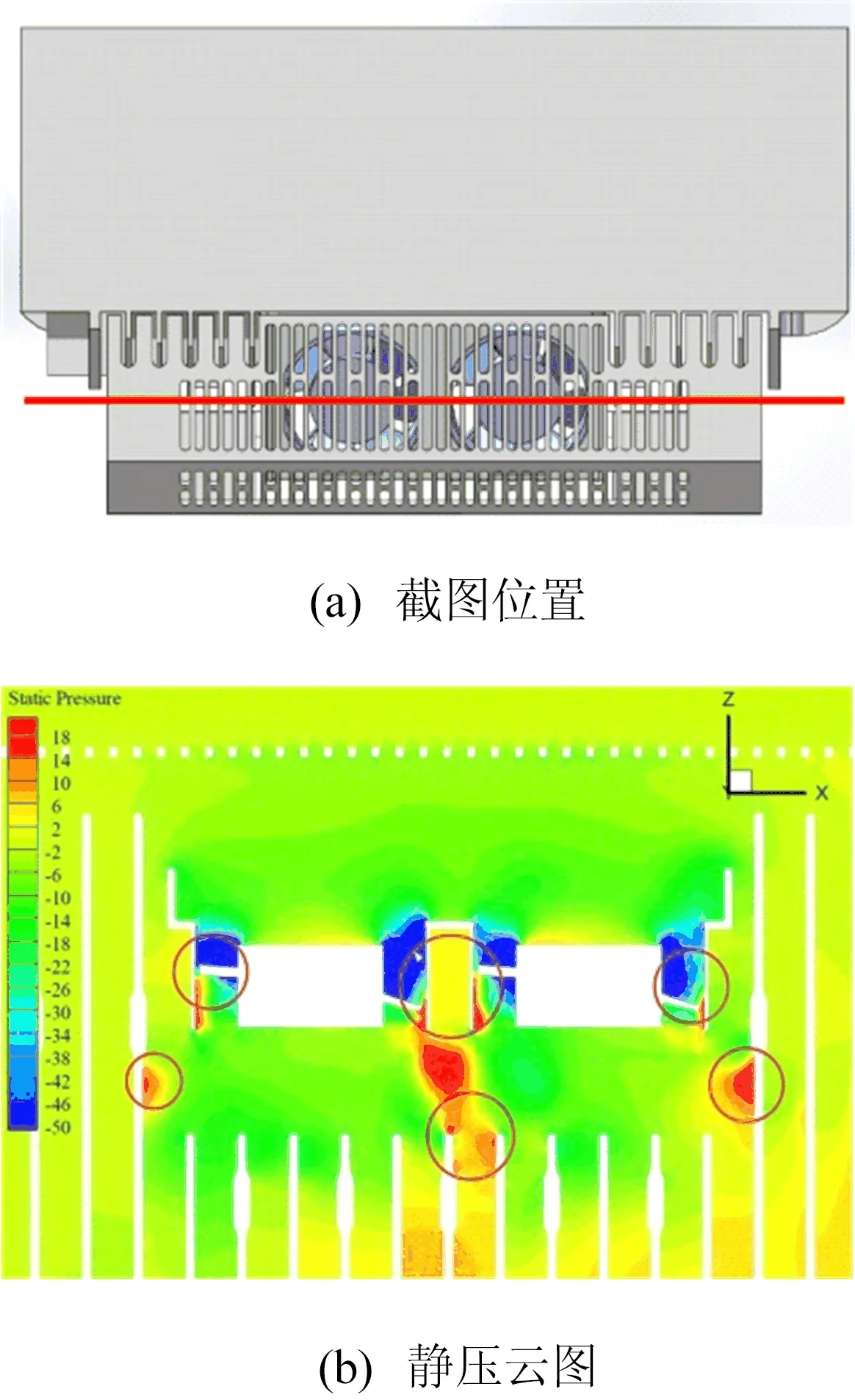
图6 流道内截面静压云图
从图6b可以看出,图中标出来的位置是流道内压力波动最大的区域,主要位于风扇周围和距离风扇出风口近的散热翅片处。其中:靠近风扇吸力面的区域形成很大的负压区,压力面附近是正压区,因为在该位置产生较大的压力波动,所以在风扇附近会形成较大的涡流,气流在轴流风扇附近有很大的扰动;其他区域的压力无论从数值大小还是波动范围上都是较小的。一般压力波动大的区域会形成湍流,会对噪声产生一定的影响。
2 气动声学数值计算
目前,气动噪声的数值计算方法可以分为以下3种[9]:计算气动声学方法、莱特希尔声类比方法和混合计算方法。考虑到本文所研究的实际模型主要噪声源处于结构体内部,声源周围的结构对声场的影响不容忽视,因此本文所采用的方法是混合计算方法,可以将模型壁面对声辐射中的散射和反射考虑到数值计算中。
2.1 声学计算方法
因为风扇是主要的噪声源,所以在进行混合计算时,噪声源选为风扇叶片。使用Fluent计算得到2个风扇表面的压力脉动数据,然后将其作为等效声源计算的输入量。在LMS.Virtual.lab中定义扇声源时,叶片相对于声波波长非常小时,可以当作一个声源来处理,但是实际情况中,叶片尺寸一般较大,因此对其进行分段处理,每个分段等效为1个源,分段结果如图7所示。
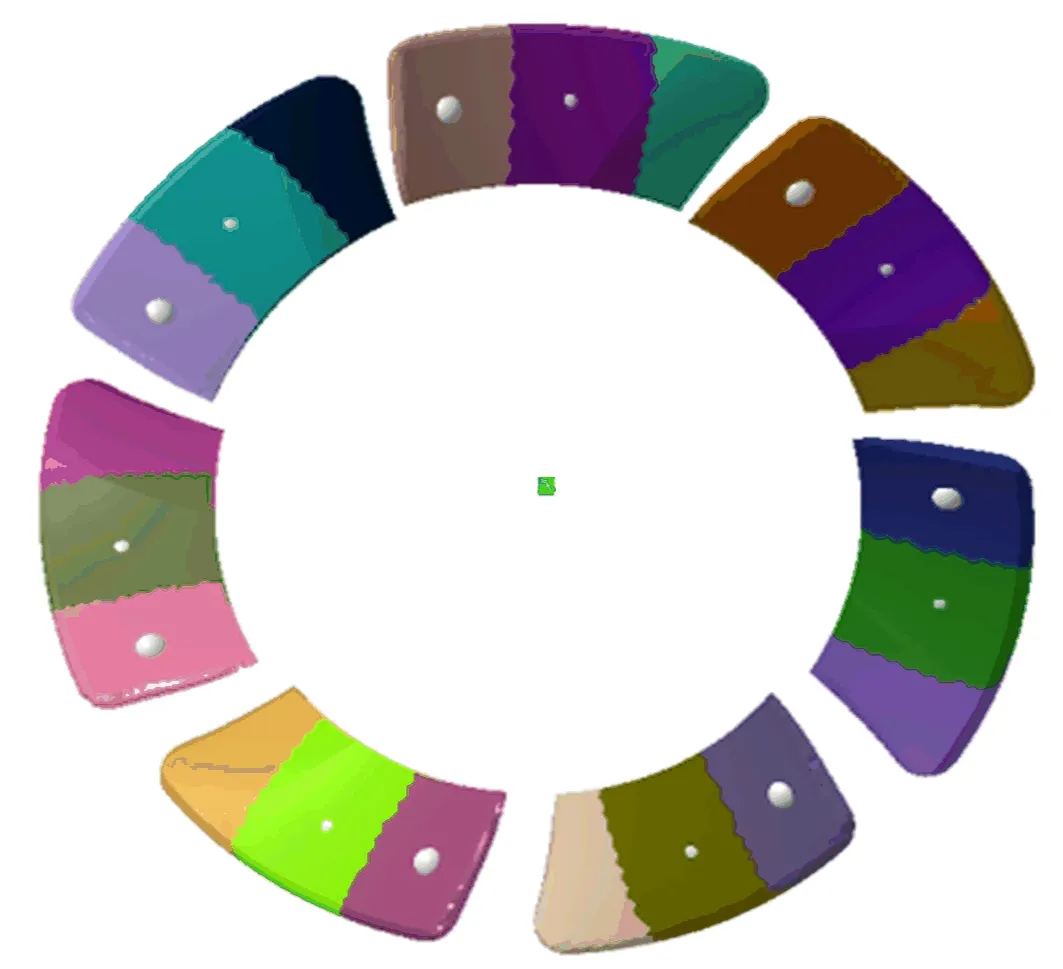
图7 等效声源划分结果
根据对叶轮机械气动噪声声源类型的分析发现,可以将轴流风扇的噪声分为单极子噪声源(叶片厚度噪声)、偶极子噪声源和四极子噪声源。经过估算流道内马赫数,其值远远低于考虑单极子声源的阈值0.6和考虑四极子声源的阈值0.8[10],因此只需要考虑叶片表面压力脉动产生的等效偶极子声源。
对声场计算空间进行离散时,采用完美匹配层(automatic matched layer,AML)技术将空间区域进行截断处理,在封闭区域内建立声学网格,如图8所示。
图8中:划分的声学体网格为10 mm;单元总数为1.20×106。假设流体声速为340 m/s,理论计算最高频率为5 666 Hz,基本包括了基频和二、三阶次谐波,满足分析要求。

图8 声学计算模型
离散场点的定义参考GB/T6882—2016标准[11]定义20个场点,这些场点位于一个2 m的半球面上,之后通过声学有限元方法计算各个场点的响应函数。
2.2 声场特性分析与实验验证
实验测试方法参考GB/T6882—2016标准[11]进行测量,测试需要在消声室或半消声室内进行,测量面选择半球面,一共是20个测点。实际测试时,保证同仿真的实际工况一样,将样机平放置在半消声室地面上进行测试,并让2个风扇保持9 000 r/min的转速运行到稳定状态,然后进行测试,如图9所示。

图9 实验测试
风扇的基频和谐波的计算公式为:
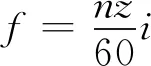
(5)
其中:n为风扇转速;z为风扇叶片数;i为谐波序号。计算得到风扇9 000 r/min所对应的基频为1 050 Hz,二次谐波为2 100 Hz,三次谐波为3 150 Hz。
20个测点处声压平均后的1/3倍频图如图10所示。
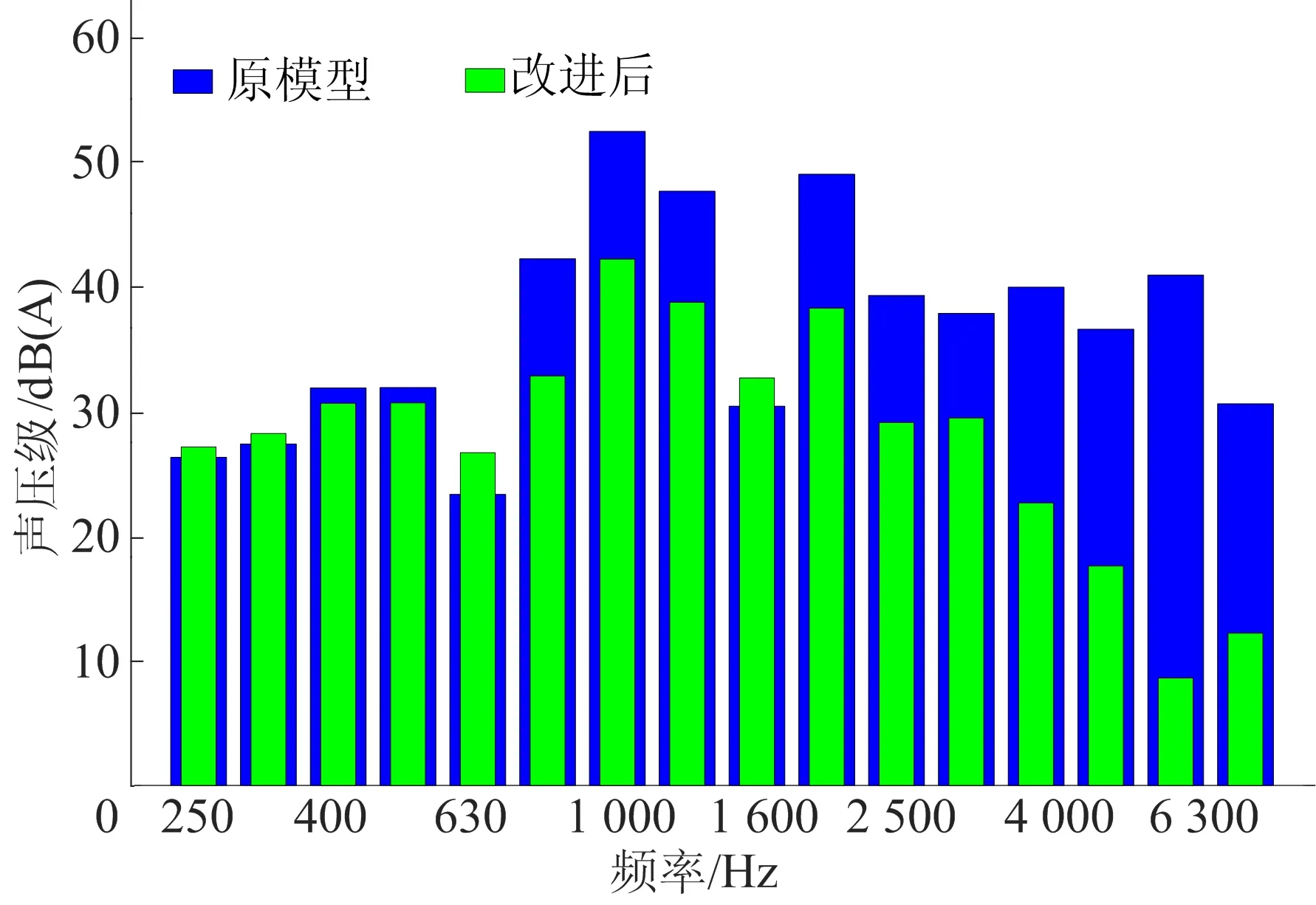
图10 1/3倍频图对比
将实验和仿真结果进行对比可以发现,在风扇通过频率处的倍频带声压级明显大于其他频带,进一步验证了整个频带内风扇谐频噪声贡献最大,而且这些频带的声压级误差较小,最大误差不超过4 dB,基本接近实验数值。除此以外,某些噪声频率段有误差较大的问题,主要原因在于整个散热系统的噪声由风扇的离散单音和宽频噪声组成,宽频噪声中主要包含壁面压力波动产生的辐射噪声以及流道内的空间四极子噪声,同时由于风扇固定架可能会产生振动,也会产生辐射噪声,而实际进行声场计算时未考虑这些因素的影响,因此数值仿真结果和实验结果在宽频内一致性不好也是较为合理的。
各测点处A计权总声压级的计算公式为:

(6)
其中:i为1/3倍频程中心频率序号;n为1/3倍频程中心频率总个数;Lpi为1/3倍频程中心频率处的声压级;Lp为总声压级。
通过计算得到20个测点处的A计权总声压级,并且与实验测试的数据进行对比,结果如图11所示。从图11可以看出,整体的声压级误差较小,而且20个测点的整体趋势也符合实验测试得到的声压级,说明了数值仿真模型的可靠性和合理性。
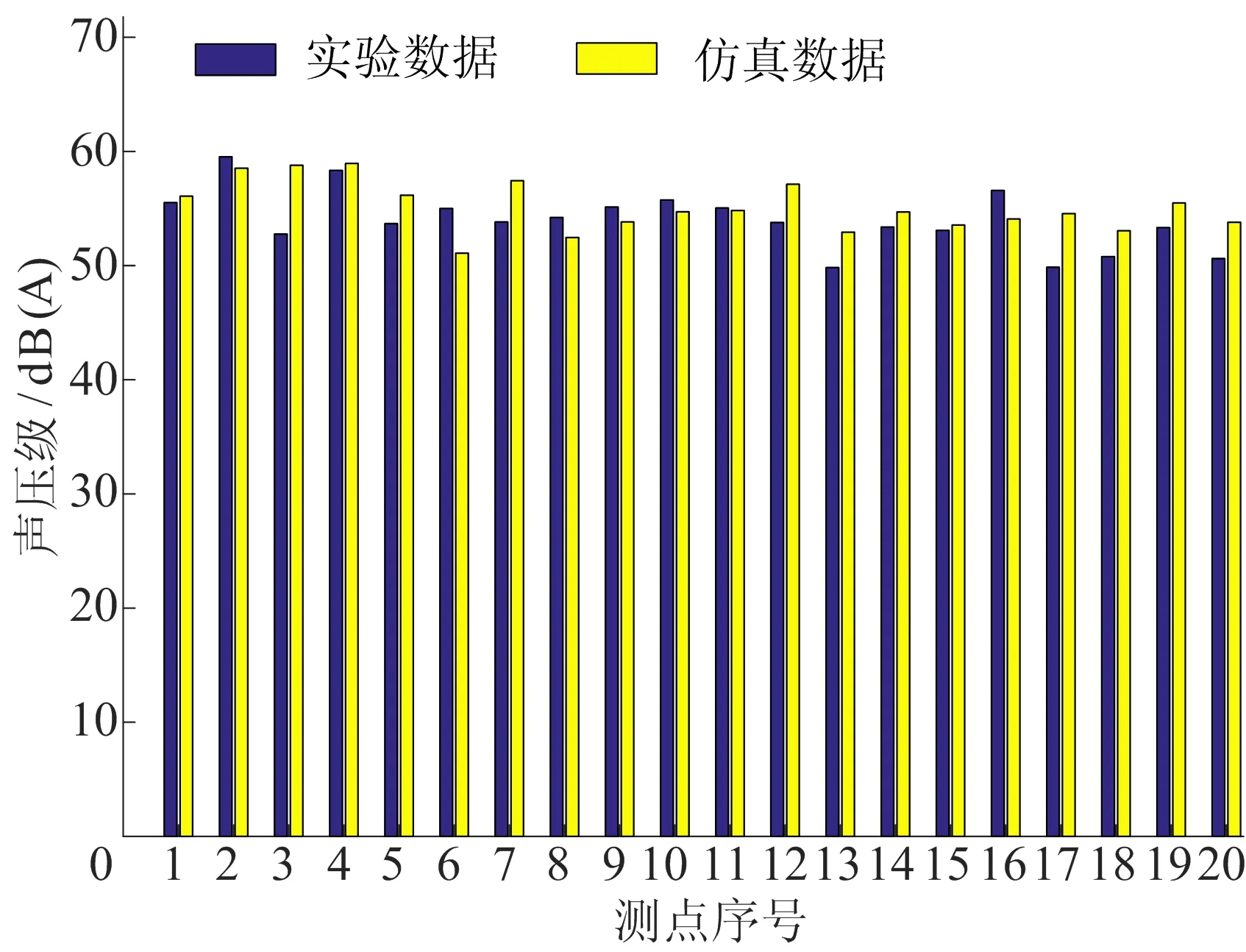
图11 总声压级对比
参考GB/T6882—2016标准[11]中声功率级计算公式,计算出声源辐射噪声的声功率级,用于衡量噪声源的强度,即
(7)
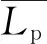
3 进气格栅对气动噪声的影响研究
从上述分析结果可以看出,风扇是主要的噪声源。实际产品制造过程中,风扇是标准件,光伏逆变器生产厂家无法对风扇本身进行自主优化设计,但由于进气口距离轴流风扇较近,进气格栅会使散热风扇进气气流不均匀,从而产生较大的湍流和漩涡,影响风扇表面的压力脉动,进而产生较大的噪声。
为了验证上述推测的合理性,对进气格栅是否影响轴流风扇表面的压力脉动进行分析研究,同时对比分析有、无进气格栅对整体气动噪声的影响。
进气格栅改进前、后的对比如图12所示。

图12 进气格栅改进前后对比
3.1 进气格栅对流场的影响分析
按照相同的条件进行仿真计算并观察风扇吸力面的静压,得到改进前、后风扇模型静压云图,如图13所示。
从图13可以看出,多个叶片表面的负压区域范围明显减小,压力波动的范围也有所减小,说明进气格栅对风扇表面的压力脉动影响较大,在去掉进气格栅以后,气流流入更加均匀,压力波动也有所减弱。结合之前对压力波动的分析,压力波动会影响噪声的大小,因此可以推断改进后的模型噪声水平会有所降低。

图13 改进前、后风扇模型静压云图
改进前、后声源表面声压级云图对比结果如图14所示。
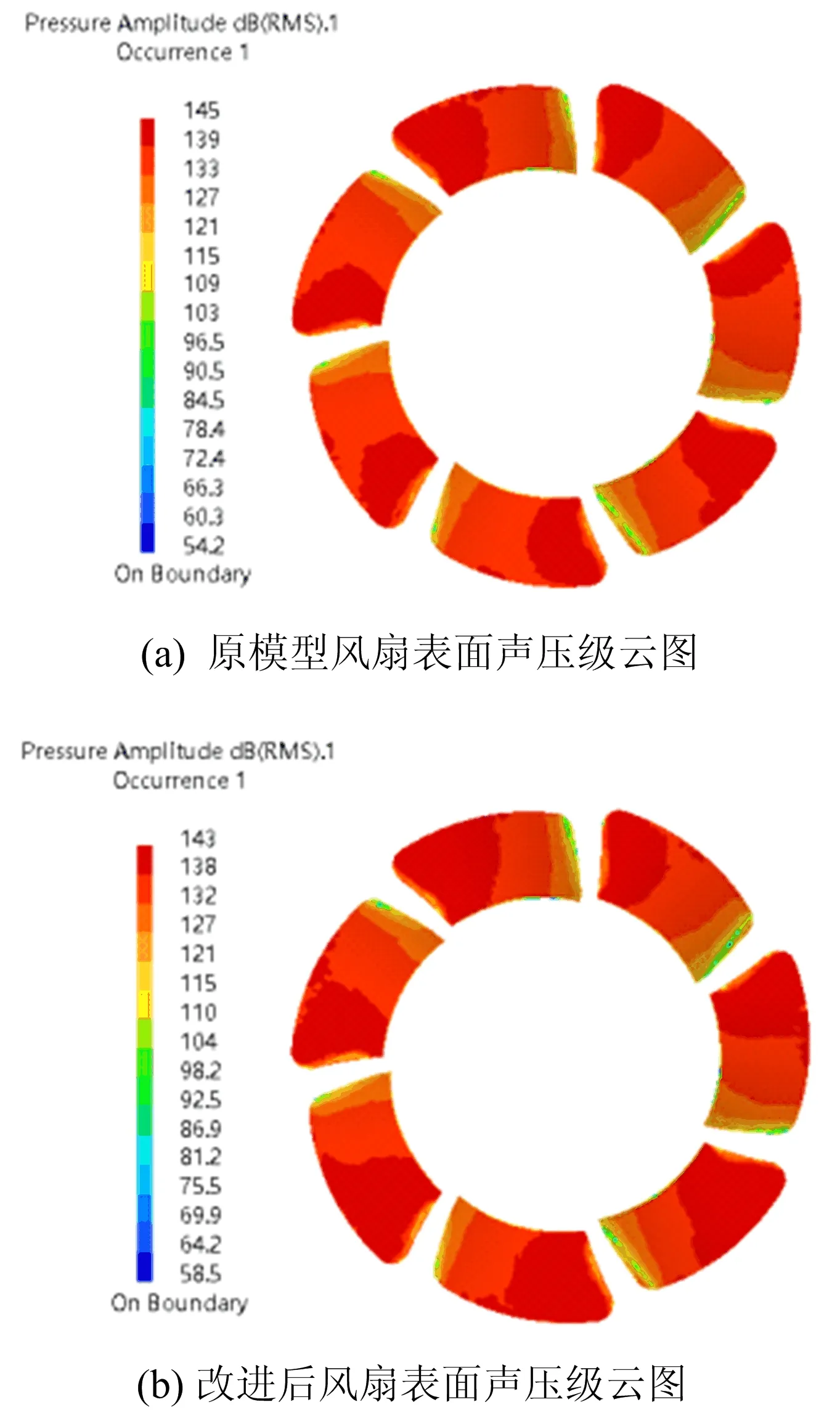
图14 改进前、后声源表面声压级云图
由图14可知,声压级云图改进前、后趋势一致,但是改进后声源面最大的声压级降低了2 dB。从流场仿真计算中对出口流量的监控发现,在去掉进气格栅以后,风扇出口流量保持在0.046 5 kg/s,与带有进气格栅的风扇出口流量基本保持一致,主要是因为没有对风扇做改动,从而能够保证对散热效果没有太大影响。
3.2 进气格栅对声场的影响与降噪效果验证
声场仿真计算使用同样的方法和参数,得到1/3倍频图和各测点的A计权总声压级,再与原模型计算得到的结果进行对比,如图15所示。
从图15可以看出,大多数频带声压级都有明显的下降趋势,尤其是高频段的声压级下降较大,而且在风扇的通过频率段声压级下降得也较为明显。这说明在改进进气格栅以后,风扇叶片自身的压力脉动有所减小,进而使得噪声辐射水平出现了明显降低。

图15 1/3倍频图数值计算结果对比
改进前、后总声压级对比如图16所示。由图16a可知,仿真模型总声压对比中,所有测点的A计权总声压级相较于改进前都有所减小,声压级最高降低4.9 dB(A),最小降低0.84 dB(A)。
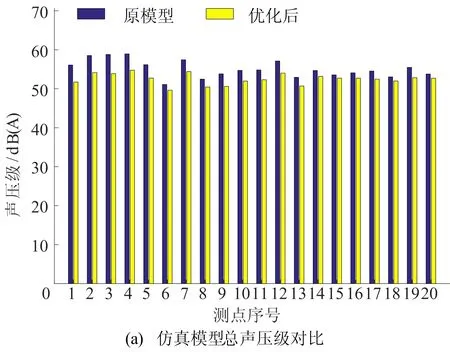

图16 改进前、后声压级对比
根据仿真的几何模型,将实际的原模型进行改进,在相同的条件下进行实验测量,并按照之前的方法计算出总声压级,并与原模型进行对比,结果如图16b所示。由图16b可知:所有测点总声压级都有所降低,最大降低2.36 dB(A);使用(7)式计算得到声功率级为67.21 dB(A),对比原模型降低了1.95 dB(A)。
4 结 论
本文以光伏逆变器作为研究对象,对其散热系统产生的气动噪声问题进行分析研究,在研究中考虑风扇周围结构对风扇的影响,采用混合仿真的方法对散热系统的流场和声场进行数值仿真计算。通过对流场计算结果和声场计算结果的分析发现:
(1) 风扇叶片间的漩涡主要出现在叶片前缘位置,并朝着负压区域移动,直到最后耗散,漩涡的出现,对风扇叶片表面的压力脉动有较大的影响。
(2) 叶片表面的压力脉动和噪声的辐射水平有关,当叶片上的压力波动量大时,作为噪声源的叶片表面的声压级也会相应增大,进而提高噪声的辐射水平。
(3) 根据实验验证,采用混合方法能够较好地预测非自由场远场噪声水平,在谐频处声压级误差较小,不同位置测点的总声压级误差在可接受的范围内,基本能够满足实际工程需要。
(4) 通过对比有、无进气格栅的2种盖板发现,进气结构会对叶片表面的压力脉动产生一定的影响。当去掉进气格栅以后,叶片吸力面压力波动区域有所减小,同时对预测得到的远场声压级进行分析,噪声有减小的趋势,并通过实验验证了该趋势的一致性,说明该仿真模型能够较好地预测远场噪声的辐射水平。

