基于变系数乘积模型的股指跟踪研究

万 学

(重庆师范大学 数学科学学院， 重庆 401331)

0 引 言

随着我国经济的不断发展，股票投资进入大众视野，成为最热门的投资方式之一。如何选择成分股对股票指数进行跟踪，越来越受到人们的关注。追踪股票指数指以某一股票指数为目标，以该指数的成分股为投资对象，通过购买该成分股所构建的投资组合，用于追踪目标指数的表现。人们感兴趣的是如何用更少的投资来获得更大的回报，这启发了学者们探索如何选择较少的成分股达到跟踪股票指数的目的。

在统计学中，选择较少的成分股追踪股票指数，称为变量选择问题。对于变量选择的方法，国内外已有许多学者对此进行了全面而深入的研究，其中Tibshirani[1]在1996年提出了一种基于压缩系数的Lasso(Least Absolute Shrinkage and Selection Operator)方法，克服了传统的逐步回归法、最优子集选择法等方法的不足，为变量选择领域的发展做出了十分重要的贡献。但是，Lasso方法在很大程度上压缩了变量的系数，致使模型偏差较大，且不具有Oracle性质。为了改善这些不足，Fan等[2]提出了能同时选出显著变量和得出相应参数估计的SCAD(Smoothly Clipped Absolute Devation)方法，并在线性模型中证明了该方法的Oracle性质；Zou[3]对不同的系数施加不同的权重进行压缩，提出了Adaptive Lasso方法，在一定程度上克服了Lasso方法的不足。但是，Adaptive Lasso方法对于处理具有组效应的数据仍然不理想。为了处理具有组效应的数据，Zou和 Hastie[4]提出了Elastic net方法，但是该方法不具有Oracle性质；为此，Zou和Zhang[5]受Adaptive Lasso方法的启发提出了另一种具有Oracle性质的方法，即Adaptive Elastic net方法。这些选择重要变量的方法已经被研究得相对成熟了，并且被学者们应用于各个领域。

在统计分析中，经常会遇到一些非负数据，例如股票价格、患者的寿命、生存时间等。处理这类数据,通常会考虑如下乘积模型：

(1)

其中，Xi是p维协变量，Yi是响应变量，β是未知参数向量，εi是严格非负的随机误差。

对于模型式(1)的估计方法,Chen等[6]基于相对误差思想，提出了最小绝对相对误差(Least Absolute Relative Errors, LARE)准则：

LARE(β)=

(2)

通过最小化目标函数式(2)可获得模型式(1)的参数估计。张丹[7]将LARE准则和文献[1-3]中提到的变量选择方法结合起来，讨论了模型式(1)的变量选择问题，并对相应的Oracle性质进行了证明。虽然Chen等[6]提出的LARE准则在一定条件下能得到具有相合性和渐近正态性的参数估计，但是LARE准则的目标函数式(2)并不光滑，且计算十分复杂，为了克服这些不足，Chen等[8]考虑将目标函数式(2)中两种相对误差相乘提出了最小乘积相对误差(Least Product Relative Error, LPRE)准则，即最小化以下目标函数：

LPRE(β)=

(3)

从目标函数式(3)可以看出，相比于LARE准则，LPRE准则的目标函数具有无限可微且严格凸的优点，这使得该目标函数具有唯一的最小值点。Chen等[8]也通过数值模拟和实例应用证明了在一定条件下LPRE估计方法比LARE估计方法更有效；李翠平[9]基于LPRE准则，通过Adaptive LASSO,Adaptive Elastic Net,以及SCAD方法研究了模型式(1)的变量选择问题，并对相应的Oracle性质进行了证明；陈银钧等[10]将LPRE准则和LASSO方法结合起来研究了模型式(1)的变量选择问题。基于LARE和LPRE准则，已有许多学者研究了线性乘积模型。但是，仅使用这个模型不能完全反应实际应用中变量之间复杂的潜在关系。胡大海[11]在LPRE准则的基础上,研究了变系数乘积模型的非参函数估计问题。

近年来，乘积模型变量选择问题得到了广泛关注，但是对于变系数乘积模型的变量选择问题的研究还鲜少出现。因此，本文将在已有文献的基础上，将LPRE和SCAD方法应用于变系数乘积模型，研究该模型的变量选择问题，并通过模拟仿真证明所提方法的有效性；最后，利用模拟中的方法追踪深证红利指数，证明所提方法的实用性。

1 模型及方法介绍

1.1 变系数乘积模型简介

当假定参数模型成立时，模型式(1)具有较高的推断精度，且具有容易解释的优点，但是在实际应用中，学者们并不能确定数据服从怎样的模型，如果假定的参数模型与实际情况不相符，对于给定参数模型的估计和统计推断就几乎没有意义。此外，模型式(1)通常是假定logY与X之间呈线性关系，但是有时候这个假定是不成立的。为此，本文考虑适应性更强的变系数乘积模型：

(4)

其中，β(·)=(β1(·),…,βp(·))T是p×1维未知函数系数向量，指标变量Ui∈[0,1]，Xi是协变量，Yi是响应变量，εi是严格非负随机误差。

对模型式(4)作对数变换，可将其转换为一般的变系数模型：

(5)

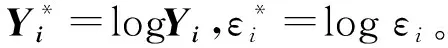
对模型式(4)进行估计，最直接的方法就是将其转换为模型式(5)，再利用最小二乘法对其进行估计，但是最小二乘法具有不稳健的缺点。同样地，对模型式(4)中的响应变量Y进行预测时，可以先对模型式(5)中的Y*进行预测，再通过指数变换得到Y的预测值，但是在这个估计和预测的过程中始终考虑的是绝对误差，而在实际应用中，对于正响应变量，更多的是关注相对误差而不是绝对误差。因此，本文基于相对误差思想，将Chen等[8]提出的LPRE准则应用于变系数乘积模型式(4)。

1.2 估计方法

鉴于B样条基函数具有良好的理论性质，类似吕晶[13],本文利用B样条基函数去逼近模型式(4)中的未知函数系数β(·)。

令B(u)=(B1(u),…,BKn(u))T为B样条基函数，则函数系数βj(·)可逼近为如下形式：

(6)

其中，γj=(γj1,…,γjKn)T为B样条系数向量，Kn=J+m+1为基函数的个数，J为内节点的个数，m为样条的阶，{Bk(·),k=1,2，…,Kn}是线性空间Gj的一组基，其中Gj由[0,1]区间上(m+1)阶的B样条函数构成。基于函数系数βj(·)的近似形式式(6)，模型式(4)可表示为如下形式：

(7)

(8)

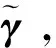
(9)

由此，求解模型式(4)中未知函数系数的估计就转化为求解模型式(8)中参数向量γ的估计。

为了选出模型式(4)中的重要变量，需要将不重要变量的系数压缩为0。由于Fan等[2]提出的SCAD惩罚函数具有将较小系数压缩为0，对较大系数不进行压缩，能使模型偏差更小的优点，且该惩罚函数是一个凸函数，能够得到全局最优解，在优化时不会陷入局部最优解，因此，本文将SCAD惩罚函数应用于变系数乘积模型。

令pλn(·)为SCAD惩罚函数，其一阶导数定义为如下形式：

其中，a>2，θ>0，λn为调整参数。为此，本文考虑以下惩罚目标函数：

(10)

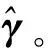
2 计算算法和调整参数的选取

2.1 LPRE参数估计的求解算法

由目标函数式(9)，容易看出该目标函数是可微的，所以最小化该目标函数就等价于求解该目标函数的一阶偏导数等于0的根，即

(11)

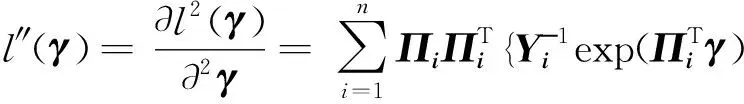
当‖γn+1-γn‖<δ时,例如δ=10-8，称迭代收敛，其中‖·‖表示向量的Euclidean范数。

2.2 SCAD惩罚估计的求解算法

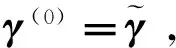
(12)

进一步，去除一些常数部分，则目标函数式(10)可以被近似为以下形式：

(13)

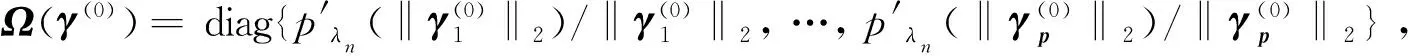
当‖γ(n+1)-γ(n)‖<δ时，例如δ=10-8，称迭代收敛。

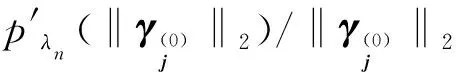
2.3 调整参数的选取

实际应用中，调整参数的选取会直接影响估计的结果，因此，选择合适的调整参数对于接下来的模拟仿真和实证研究是十分重要的。

首先，本文采用三次B样条(即m=3)，为了计算更简便，采用等距节点，并且类似明浩等[15]取内节点的个数J=[n1/(2m+1)]，其中[c]表示不超过c的最大整数；其次，基于Fan等[2]的建议，取a=3.7；最后，鉴于贝叶斯信息准则(Bayesian Information Criterion，即BIC)的良好理论性质，利用BIC准则选取最优的λn，即通过最小化以下目标函数来选取λn：

3 模拟仿真分析

考虑如下变系数乘积模型：

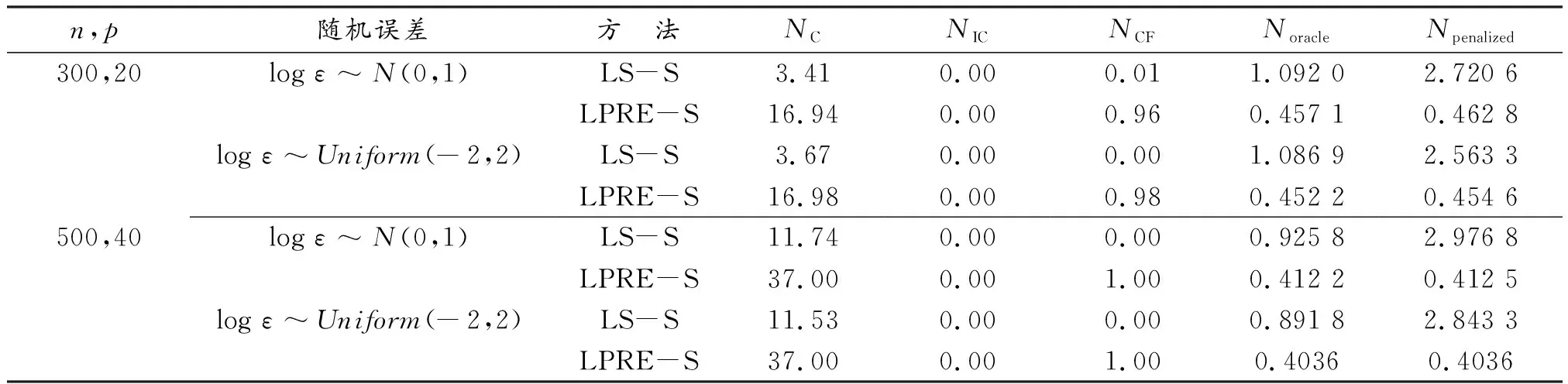
表1 模拟结果

从表1的模拟结果可以看出:对于给定的模型，两种方法的结果受不同的误差分布影响。首先，当误差的对数服从正态分布时，关于NCF与RASE值方面，LPRE-S方法比LS-S方法表现得更好，这说明了LPRE-S方法比LS-S方法更有效，且LPRE-S变量选择的结果几乎一致最好。其次，当误差的对数服从(-2,2)上的均匀分布时，仍然是LPRE-S方法的结果更好，且相比于logε服从标准正态分布时，LPRE-S方法和LS-S方法的结果都稍好一点。最后，当样本量增大时，LPRE-S估计方法选出真实模型的比率随之提高，几乎接近1，且NPenalized与NOracle更加接近，这充分说明了本文所提方法的有效性。

4 实证研究

为了进一步说明所提方法的实用性，将所提LPRE-S方法应用于股票指数的跟踪，选取深证红利指数及其成分股作为实证研究对象。深证红利指数是指40只能够为深圳股市投资者提供长期稳定回报的股票,是深圳巨潮红利指数的缩影。本文数据来源于西南证券金点子财富管理终端，采用2019-01-02—2021-02-26期间，深证红利指数及其40只成分股的522个日线收盘价数据进行研究。

将深证红利指数作为响应变量Y，40只成分股作为协变量X，成分股中的鞍钢股份作为指标变量U，考虑随机模拟中的LPRE-S和LS-S两种方法，同时对所有协变量进行标准化。由于影响股票指数的因素较多，且作用机制较复杂，这使得预测股票指数的长期走势非常困难，但是在短期预测中往往能够取得较好的效果。因此，为了检验模型的预测能力，令T=0,1,…,121，取第1天到第(400+T)天的数据作为训练集，利用训练集获得参数和非参函数的估计，然后通过训练集上获得的预测模型来预测第(400+T+1)天的深证红利指数，从而得到第401天到第522天的122个预测值，其预测效果如图1、图2所示。

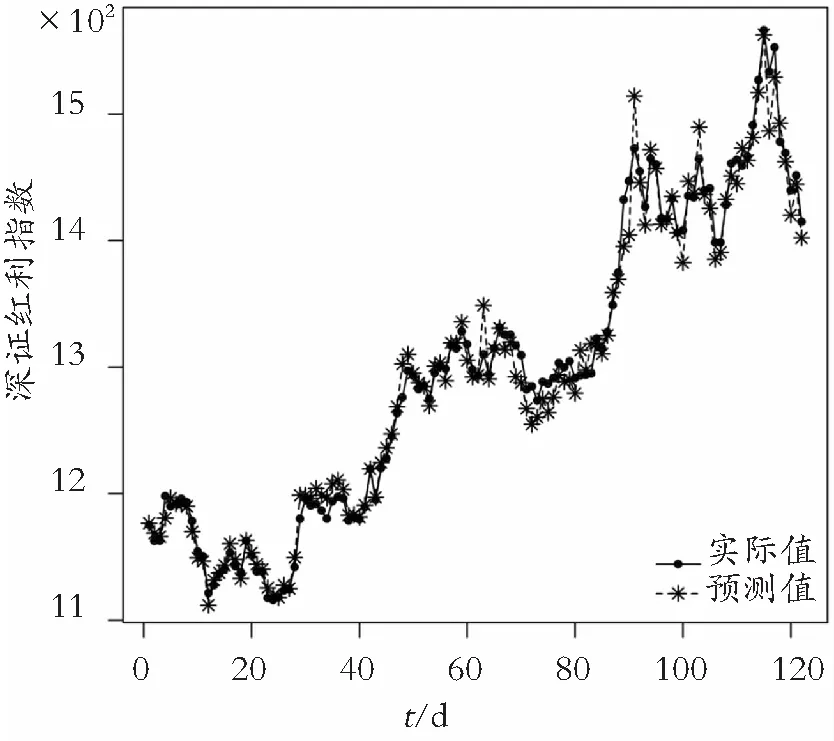
图1 LPRE-S方法实际值与预测值走势图

图2 LS-S方法实际值与预测值走势图

通过观察图1、图2，发现在前60天的预测中，LPRE-S方法的实际走势与预测走势几乎一致，易见其预测效果优于LS-S方法，而后62天，LPRE-S方法预测效果没有前60天预测效果好，且后60天两种方法的预测效果差别不是很明显。但是，通过计算得到，LPRE-S方法在第401天到第522天所得残差平方和为2 219 764，LS-S方法在第401天到第522天所得残差平方和为3 322 961，即LPRE-S方法的残差平方和要小于LS-S方法的残差平方和。

为了进一步对以上两种估计方法的预测效果进行比较，类似Chen等[8]建立以下4种中位数指标评价LPRE-S估计方法和LS-S估计方法：

表2 LPRE-S和LS-S两种方法预测误差的中位数比较结果

对于表2中的4种中位数指标，值越小的方法，其预测效果越有效。从表2的结果可以看出：LPRE-S方法在每种中位数指标下的值都比LS-S方法的值小，即LPRE-S方法的结果优于LS-S方法。由此，进一步说明了本文所提方法能更加有效追踪股票指数。

5 结 论

本文基于B样条函数逼近技术，将LPRE准则和组SCAD惩罚函数结合起来，应用于变系数乘积模型，利用牛顿迭代法和局部二次近似给出了所提方法的计算算法，并阐释了如何选取调整参数。通过数值模拟对LPRE-S估计方法和LS-S估计方法进行了比较，发现LPRE-S估计方法选出真实模型的比率几乎接近1，且NPenalized与NOracle十分接近，这说明了LPRE-S估计方法能更好地达到变量选择的目的，证明了所提方法的有效性。为了进一步说明所提方法的实用性，用LPRE-S估计方法实现了对深证红利指数的跟踪预测，并与LS-S估计方法的预测效果进行了对比。通过比较122个预测值的残差平方和与4种不同的预测误差中位数指标，发现LPRE-S估计方法效果优于LS-S估计方法，说明了本文所提方法在股指跟踪中具有较好的预测效果。