基于自适应网格混合机制的多目标粒子群算法
邹康格, 刘衍民
(1.贵州大学 数学与统计学院,贵阳 550025;2.遵义师范学院 数学学院,贵州 遵义 563006)
0 引 言
当今多数科学和工程问题通常有多个目标,决策者需要同时使多个目标在给定的范围内尽可能得到最佳优化,即多目标优化问题。在多目标优化问题中,由于各目标之间存在冲突,多目标优化问题不存在唯一的最优解,因此分析一个多目标优化问题的目标是找到一组非劣解而不是单个解,非劣解也称为帕累托解,且一组非劣解构成了客观空间中的帕累托前沿,因此解决多目标优化问题的核心目标就是使这些非劣解尽可能接近真实的帕累托前沿且保持分布均匀。粒子群算法(PSO)由于收敛速度快,易于实现,在许多单目标优化问题中得到广泛应用,并取得了良好的效果。当PSO运用于多目标优化问题时,即多目标粒子群算法(MOPSO),在解决多目标问题中由于MOPSO算法收敛速度快,容易导致种群陷入局部最优解,使得算法早熟收敛。对于上述问题,有很多学者提出了改良的多目标粒子群算法:在文献[1]中,提出带有随机迁移的多目标粒子群算法,该算法设置一个年龄阈值,当一个粒子没有改良它的个体位置时,会增加它的年龄,并且当粒子年龄超过这个年龄阈值时,粒子将被重新初始化,以此提高种群多样性,但分解替换占优关系,在解决一些复杂的多目标优化问题时,表现不佳。在文献[2]中,提出一种改进的时变参数跟随蜂搜索的多目标粒子群算法,应用个体最优解的权重随着迭代的进行而逐步减小,该方法消除了相对于全局最优解质量较差的影响,提高了算法的收敛能力,但在解决多局部前沿的多目标优化问题时存在困难,且非劣解多样性较差。在文献[3]中,提出一种基于健康度的多目标粒子群算法,该算法定义了健康度的概念,当粒子越来越接近最优解时,该粒子健康度上升,反之下降,使得粒子跳出局部最优,虽然该算法能保证种群的多样性和在Pareto前沿上分布均匀,但算法仍存在收敛性不足的问题。在文献[4]中,提出一种动态多个子群的多目标粒子群算法,该算法通过动态群策略自适应地调整搜索过程中粒子群的数量,该算法根据需要分配适当数量的蜂群,以支持蜂群之间的收敛性和多样性准则,但种群数量的增长速度不够高,缺乏良好的策略来加强种群之间和种群内部的交流。
上述算法的有效性在一定程度得到了提升,但是,当面对复杂的多个目标且多个变量的优化问题,算法极易出现早熟收敛。为了解决这个问题,进一步提升MOPSO算法的性能,本文提出基于自适应网格混合机制的多目标粒子群算法(ammmMOPSO)。对MOPSO主要改进包括:为保障种群的收敛性和多样性,在使用网格技术基础上使用“加权和函数”策略去挑选全局最优样本;在外部存档中使用“加权和函数”和相邻距离的混合机制删除外部存档中的粒子,以提高非劣解的质量;为了保证粒子有跳出局部最优的能力,使用一种变异操作策略对粒子位置进行变异。仿真实验结果表明,所提出的改进算法是对多目标粒子群算法的有效改进。
1 多目标优化问题与粒子群算法
1.1 多目标优化问题
一般多目标优化问题的定义描述如下:
其中,x=(x1,x2,…,xn)T是n维决策向量,fi:Rn→R,i=1,2,…,k是目标函数,gi,hj:Rn→R,i=1,2,…,m;j=1,2,…,p分别是不等式约束和等式约束。
1.2 基本粒子群算法
PSO通过在规定范围内随机初始化一个均匀分布的粒子,群体中的全部粒子都具备影象功效,每一个粒子都有自己的位置和速度,且由全局最优粒子(gbest)和个体最优粒子(pbest)驱动粒子寻找最优解。在单目标粒子群算法中,由于只有一个目标函数,只需比较其适应度值就可以唯一确定gbest和pbest。在多目标粒子群算法中,关于选择pbest,如果粒子的每个目标都好则该粒子更优,如果不能严格对比谁更优则随机选择其中一个作为个体最优;关于选择gbest,有很多的非劣解都可以作为全局最优个体,然而在PSO中,每个粒子只能选择一个作为全局最优个体,因此保存这些非劣解和挑选出较好的一个非劣解是粒子群算法处理多目标优化问题的核心。粒子的速度和位置更新方程如下:
v(t+1)=ωv(t)+c1r1(p(t)-x(t))+
c2r2(g(t)-x(t))
(1)
x(t+1)=x(t)+v(t+1)
其中,ω是惯性权重,它的大小控制着搜寻本领的大小;c1、c2分别是个体经验系数、社会经验系数;r1、r2是在范围[0,1]之间的随机数;p和g分别是个体最优解、全局最优解。
2 改进算法
全局最优样本的选取、外部存档规模的控制和粒子的变异操作是粒子群算法处理多目标优化问题的主要改进部分。本文在全局最优样本选取部分,提出自适应网格和“加权和函数”策略,并结合“加权和函数”和相邻距离的外部存档维护,提出一种变异操作对粒子的位置进行变异,进一步改善多目标粒子群算法的性能。对于自适应网格的方法,请参考文献[5]。
2.1 基于加权策略的全局最优样本选取
在多目标粒子群算法的每一次迭代中都会产生很多的非劣解,由于它们互不占优,很难选择出最优的粒子,所以需要考虑保障非劣解解集的多样性。为了保障非劣解解集的多样性,本文使用“加权和函数”F(x)和轮盘赌策略对同一个网格中的粒子选出全局最优样本。
首先粒子的所有目标值使用一个标准化的过程,标准化过程可以通过将每个目标函数除以其最大值来实现;由于搜索空间已知,可以很容易地计算出每个目标函数的最大值;其次该粒子的所有目标函数标准化后,得到一个“加权和函数”F(x)是该粒子的所有目标函数标准化之和。
粒子的每个目标函数权重为粒子的每个目标值分别除以在所有粒子中所对应目标函数的最大值。其定义如下:
其中,fm(x)为粒子x第m个目标函数值,Fm为所有粒子在第m个目标函数值中的最大值。
粒子的标准化过程为粒子的每个目标函数权重乘以其对应的目标函数值。
粒子的每个目标函数权重乘以其对应的目标函数值之和作为该粒子的“加权和函数”值,其定义如下:
(2)
其中,fm(x)为粒子x第m个目标函数值,wm为粒子x第m个目标函数权重,M是目标函数个数。
为了说明在同一网格的非劣解中“加权和函数”值越小,则该非劣解粒子处于网格中所有粒子的中心位置(中心粒子)或者越接近网格中央;假设在同一网格中有5个非劣解,它们的函数值坐标分别为:P1(1,5)、P2(2,4)、P3(3,3)、P4(4,2)、P5(5,1),根据式(2)得到这5个非劣解的“加权和函数”值分别是5.24、4、3.6、4、5.2,可以得出P3(3,3)是最小的,又由P3(3,3)是中心粒子且越有可能接近网格中央的非劣解,所以在同一网格的非劣解中“加权和函数”值越小,则该非劣解是中心粒子或越可能接近网格中央的粒子。
如图1所示,其中实心圆点和空心圆点分别代表全局最优样本和非劣解,在同一网格中选取“加权和函数”值最小的粒子(网格中心粒子)作为全局最优,若有相同的最小值,则随机选择其中一个,使得本文提出的算法在搜寻过程中引导粒子分别向距离相对较远的非劣解飞行,以增强种群的多样性。
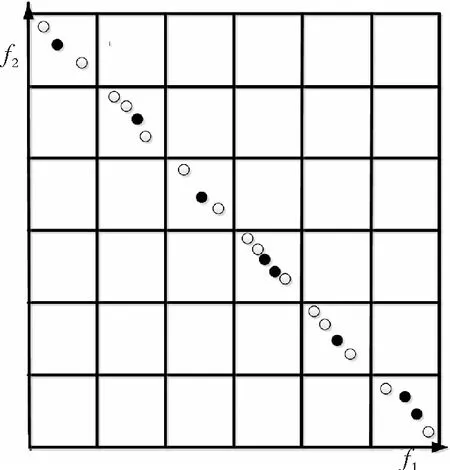
图1 全局最优样本的选取
2.2 基于混合机制的外部存档维护
在多目标粒子群算法的每一次迭代中都将非劣解储存到外部存档中,随着算法运行,非劣解的数量也随着增加,当外部存档达到饱和时,则需要对外部存档进行维护。在很多的多目标粒子群算法中都使用自适应网格策略对外部存档中的非劣解进行删选,其具体方式是找到粒子数最多的网格,随机删除网格中的粒子或者删除网格中拥挤度最大的粒子,这些策略都有可能导致非劣解分布不均匀。因此,本文提出“加权和函数”和相邻距离的混合策略,确保外部存档中的非劣解保持良好的分布,从而为全局最优解的选择提供较好的候选解。
定义粒子xi的相邻距离为粒子xi+1与粒子xi-1之间的欧式距离。在处于同一网格的粒子中,计算某粒子的相邻距离等于邻居两个粒子的欧氏距离大小,粒子的相邻距离越小,则该粒子的密度越大。其相邻距离定义如下:
(3)
在图2中,图2(a)代表外部存档中的非劣解分布情况,图2(b)、图2(c)和图2(d)分别代表随机删除、拥挤度删除和“加权和函数”与相邻距离的混合删除;在图2(b)中从非劣解数量最多的网格中随机删除40%的粒子数,这种随机性可能导致网格中的非劣解有些分散,有些拥挤;在图2(c)中从非劣解数量最多的网格中根据拥挤程度大小删除40%拥挤程度最大的粒子数,虽然保障了密度最大的网格中的非劣解分布均匀,但是有可能与其他相邻的网格中的边界非劣解比较拥挤;在图2(d)中从非劣解数量最多的网格中首先根据式(3)删除20%相邻距离最小的粒子数,其次由于在同一网格中非劣解的“加权和函数”值越大,则越可能接近网格的边界,所以再从非劣解数量最多的网格中根据式(2)删除20%“加权和函数”值最大的粒子数,这种策略既能保持密度最大的网格中的非劣解分布均匀,也能与其他相邻网格中边界粒子保持距离。比较图2(b) 、图2(c)和图2(d)可知,本文提出混合机制的外部存档维护,更好地改善了非劣解分布情况。
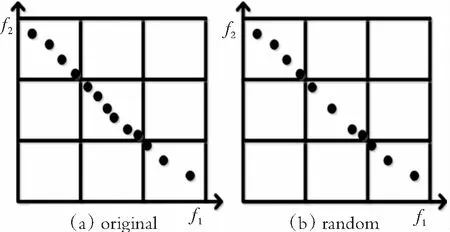
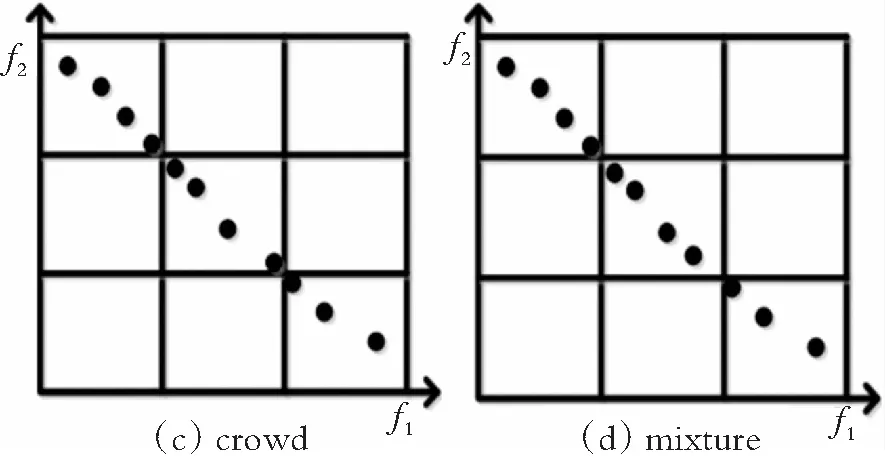
图2 外部存档的维护示意图
2.3 变异操作
MOPSO算法是一种群体智能算法,在迭代早期搜索能力较强,可以不断搜索新的领域,但MOPSO算法具有快速收敛的效果,在迭代后期该算法极有可能在局部最优解的周围精细搜索,使得该算法早熟收敛。因此,为了使算法在迭代早期保持良好的种群多样性,在迭代后期提升种群多样性,使用变异操作对位置递增程度的变异。粒子的位置变异程度随着迭代次数的增加线性递增,在迭代初期,种群的多样性良好,使粒子的变异程度较小,从而种群的多样性保持稳定,在迭代后期,种群的多样性不足,使粒子的变异程度较大,以增强种群的多样性。在ammmMOPSO算法中,粒子速度的更新公式为式(1),粒子位置的更新公式如下:
(4)
其中,N为最大迭代次数,n为当前迭代次数,e为自然对数。
2.4 算法的主要流程
算法的主要流程如下:
Step1 初始化。设置种群数目、最大的外部存档数目、粒子的维数、网格数目和最大迭代次数;随机初始化位置和速度;对每一个粒子位置初始值作为该粒子的个体最优值;创建外部存档并设为空集。
Step2 计算粒子的适应度。计算每个粒子的适应度,把非劣解储存到外部存档中。
Step3 建立自适应网格。对目标空间创建网格,分别用式(2)和式(3)计算每一个网格中的非劣解。
Step4 个体最优样本和全局最优样本的选取。个体最优样本是当前位置与个体历史最优位置之间的优者,若互不占优,则随机选择一个,全局最优样本是利用轮盘赌方法对每一个网格的非劣解中选择“加权和函数”值最小的非劣解。
Step5 更新速度和位置。对每个粒子的速度和位置利用飞行式(1)和式(4)更新。
Step6 更新外部存档。若外部存档没有到达饱和状态,则继续引入非劣解;若外部存档达到饱和状态,找到网格粒子数最多的网格,首先根据式(3)删除20%相邻距离最小的粒子数,再根据式(2)删除20%“加权和函数”值最大的粒子数,再引入非劣解进入外部存档,使得外部存档得到更新。
Step7 终止条件。若当前迭代次数小于最大迭代次数,则返回Step2,输出最优解集。
ammmMOPSO算法流程如图3所示:

图3 ammmMOPSO算法的流程图
3 实验仿真分析
3.1 性能评价指标
为了评估各算法性能。本文采用收敛性指标(GD)、分布性指标(Δ)、标准化空间指标(IH)分别对算法进行评价。GD[8]是权衡算法所获得的前沿与真实Pareto前沿之间距离大小,GD越小表示算法的收敛性越好。Δ[9]衡量算法所获得非劣解的分布情况,Δ越小表明非劣解越有均匀的分布。IH[10]衡量算法在空间中非劣解分布性情况,IH越大表明空间中非劣解分布性越好。
3.2 参数选择
ammmMOPSO算法的参数设置:种群数量设置为200,最大迭代次数为2 000次,外部存档规模大小设置为200,网格数为50,c1=c2,ω=0.4。其他3种比较的多目标粒子群算法的参数设置和原文献保持一致。
3.3 实验结果及数据分析
为了验证ammmMOPSO算法的有效性,ammmMOPSO算法与国际经典的3种多目标粒子群算法在双目标问题(ZDT1-ZDT4)和三目标问题(DTLZ2、DLTZ4和DTLZ5)上分别进行实验仿真,对比算法包括:MOPSO[5]、SMOPSO[6]和EMMOPSO[7]算法。各算法都是在同一测试函数上独立运行30次,并且均迭代2 000次所得出的实验结果。所有实验运行的环境均是在Intel(R) Core(TM) i7-7820 HQ CPU @2.90 GHZ、Windows10操作系统和MATLAB 2013a。
在4个双目标测试函数上,表1和表2分别显示ammmMOPSO算法与国际经典的3种多目标粒子群算法的GD指标和Δ指标的平均值和标准差,在3个三目标测试函数上,表3显示ammmMOPSO算法与国际经典的3种多目标粒子群算法的IH指标的平均值和标准差,其中加粗的数据表示各项指标的最好结果。
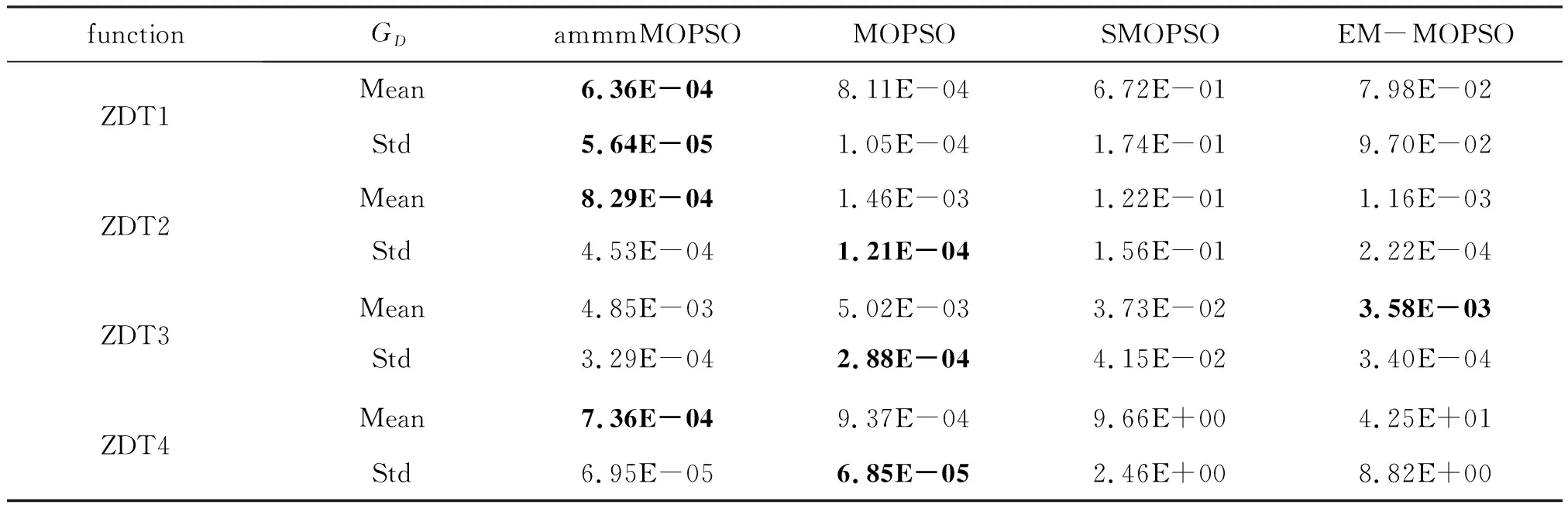
表1 不同算法在ZDT系列测试函数上的GD值
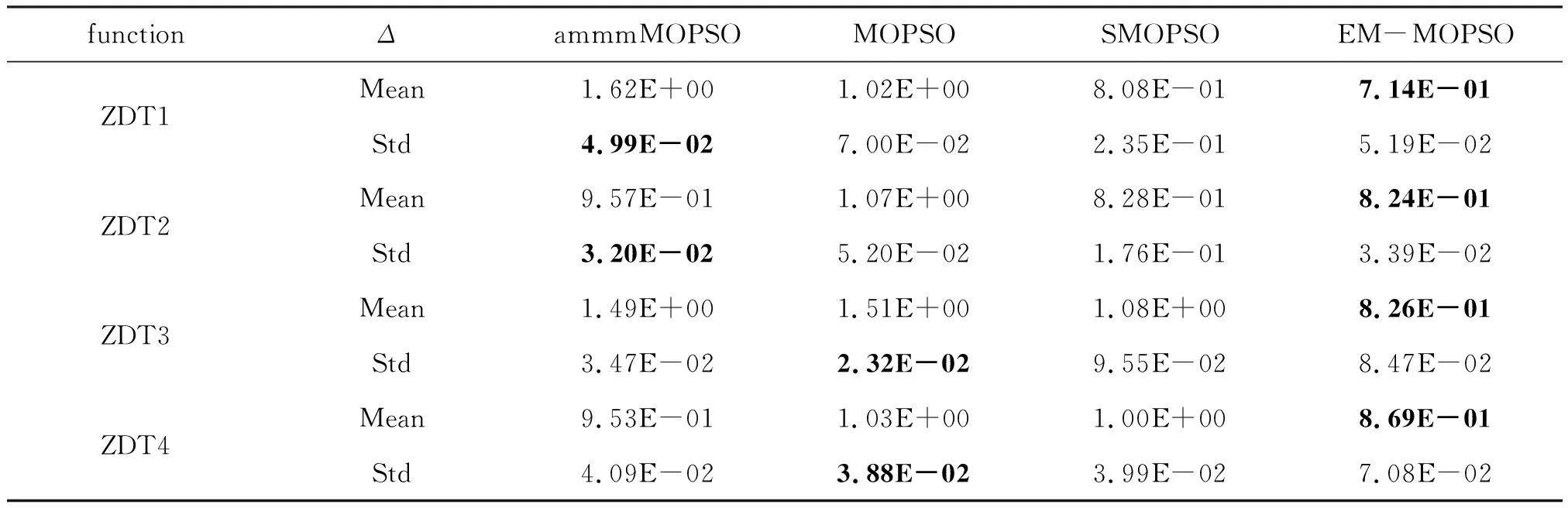
表2 不同算法在ZDT系列测试函数上的Δ值
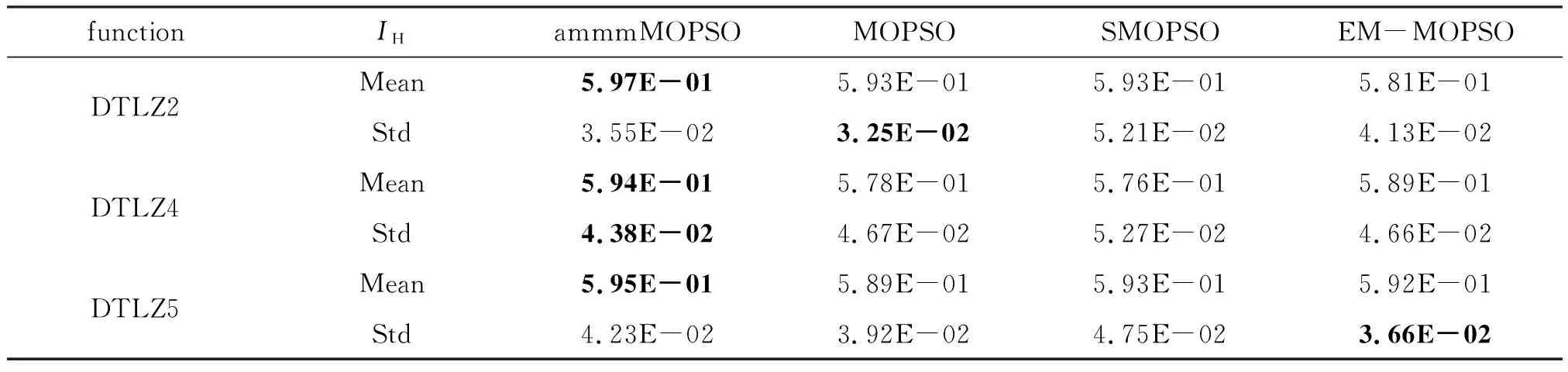
表3 不同算法在DTLZ系列测试函数上的IH值
从表1可知,在4个双目标测试函数上ammmMOPSO算法获得3个最优的GD平均值和1个最优的标准差。即使在ZDT3测试函数上ammmMOPSO算法的GD指标略低于EMMOPSO算法,但是比MOPSO算法和SMOPSO算法有着明显的收敛性优势;综上可知,ammmMOPSO算法有着良好的收敛性。正是ammmMOPSO算法在全局样本的选取部分使用“加权和函数”去筛选同一网格的非劣解,以及对粒子的位置进行变异操作,使得该算法避开局部最优解,从而获得更好的最优解。
从表2可知,在4个双目标测试函数上ammmMOPSO算法获得2个最优的标准差和2个次优的标准差,说明ammmMOPSO算法所获得的Δ数据比较稳定。在测试函数ZDT2-ZDT4上ammmMOPSO算法的Δ平均值都要低于MOPSO算法;在测试函数ZDT4上ammmMOPSO算法的Δ平均值同时低于MOPSO算法和SMOPSO算法;综上可知,ammmMOPSO算法有较好的分布性。正是ammmMOPSO算法在外部存档中使用“加权和函数”与相邻距离的混合策略,使得ammmMOPSO算法能够保留较好的非劣解并且删掉较差的非劣解,从而保障非劣解分布均匀。
从表3可知,在3个三目标测试函数上ammmMOPSO算法获得了3个最优的IH平均值和1个最优的标准差。由此看出,比其他3种多目标粒子群算法表现更加优越。
为了直观地观察各算法所得的非劣解解集的收敛性和多样性,在图4-图7中分别给出了在双目标测试函数ZDT1-ZDT4上求得的非劣解集与真实的帕累托前沿对比的图片。仿真实验结果表明,在ZDT1函数上,SMOPSO算法的收敛性略显不足,ammmMOPSO算法、MOPSO算法和EMMOPSO算法有较好的收敛性;在ZDT2函数上,SMOPSO算法表现出收敛性和多样性严重不足,ammmMOPSO算法、MOPSO算法和EMMOPSO算法都有较好的收敛性和多样性,其ammmMOPSO算法表现效果最佳;在ZDT3函数上,4种算法都有较好的收敛性和多样性,其中ammmMOPSO算法表现最佳;在ZDT4函数上,SMOPSO算法和EMMOPSO算法的多样性和收敛性都表现出严重不足,ammmMOPSO算法和MOPSO算法的多样性和收敛性表现良好;其中ammmMOPSO算法表现最佳;综上可知,ammmMOPSO算法在双目标测试函数ZDT1~ZDT4上更加接近真实的帕累托前沿且有着良好的分布。从图8—图10可以看出,ammmMOPSO算法比其他多目标粒子群算法具有更好的非劣解分布。
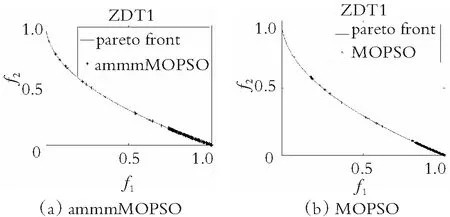
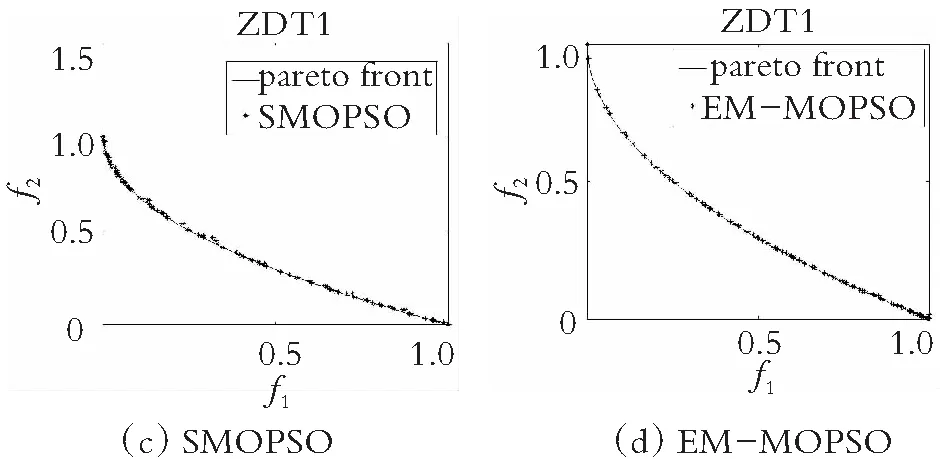
图4 对于ZDT1函数4种不同算法的真实Pareto前沿效果图
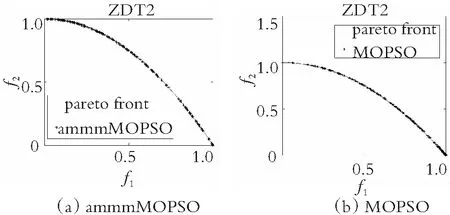
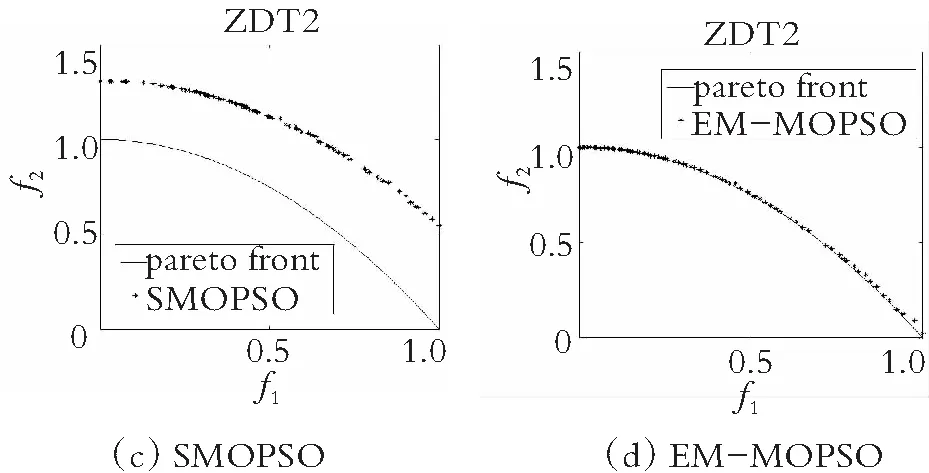
图5 对于ZDT2函数4种不同算法的真实Pareto前沿效果图
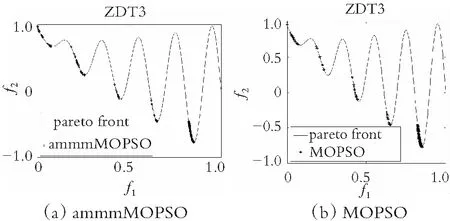
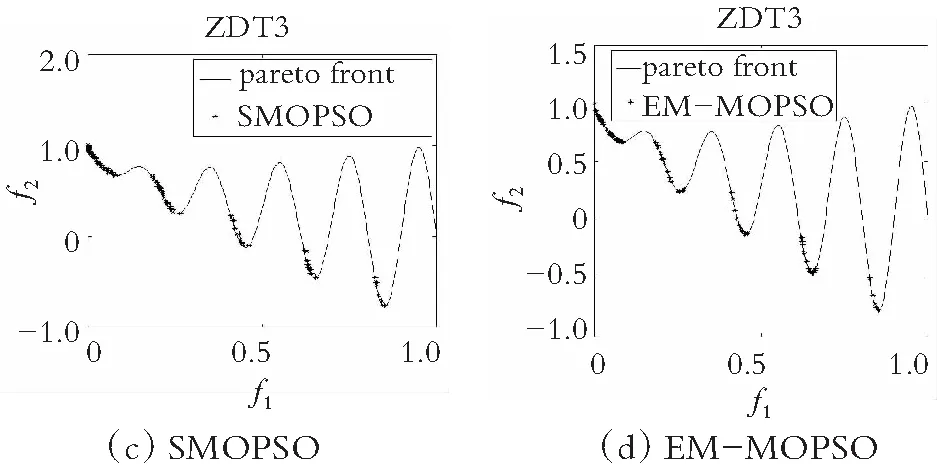
图6 对于ZDT3函数4种不同算法的真实Pareto前沿效果图
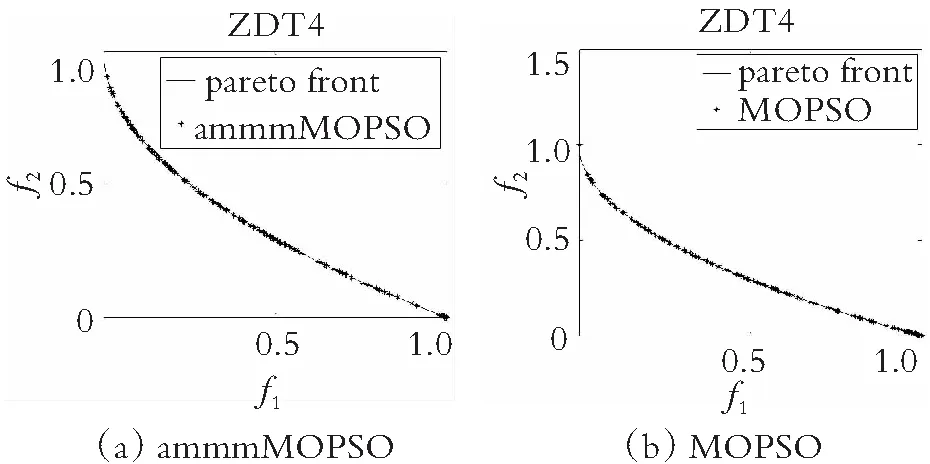
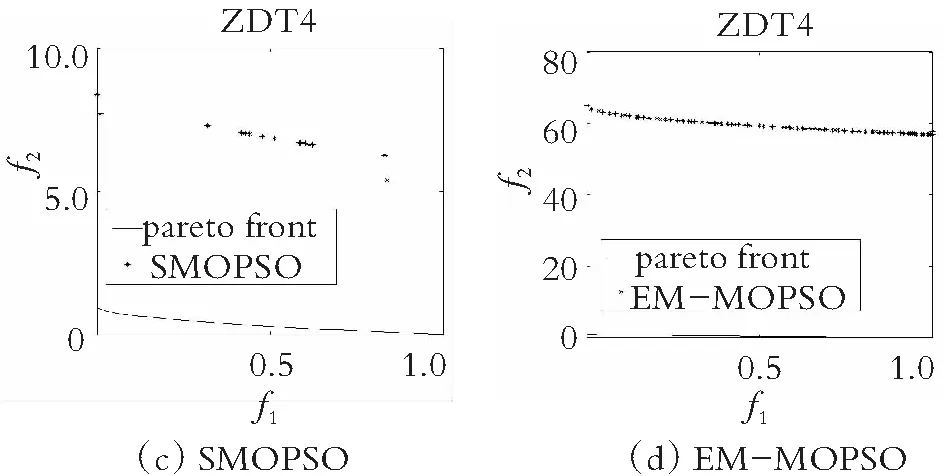
图7 对于ZDT4函数4种不同算法的真实Pareto前沿效果图
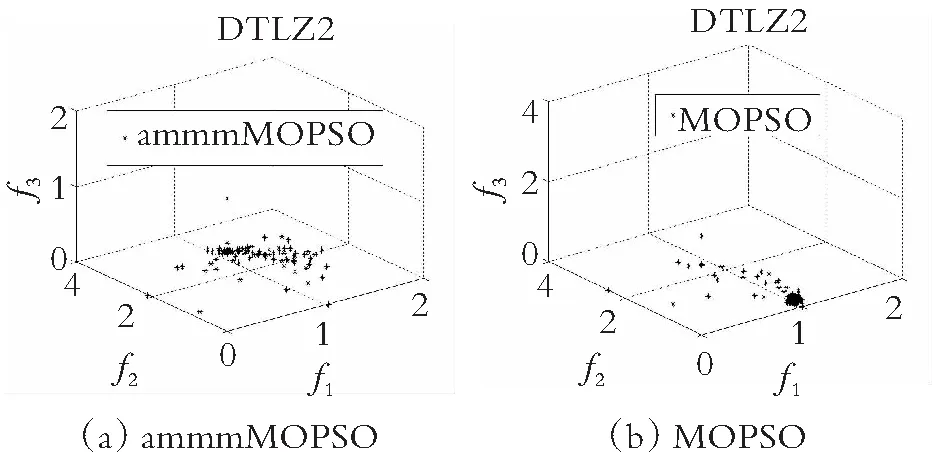
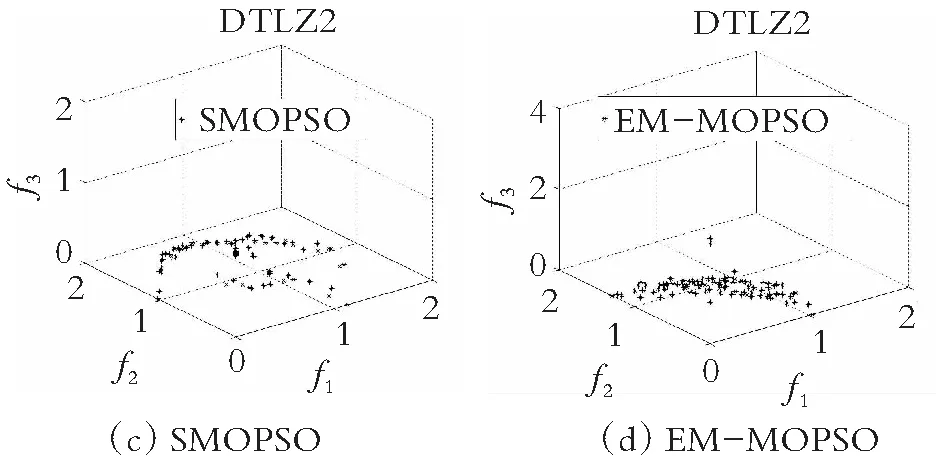
图8 对于DTLZ2函数4种不同算法的Pareto前沿效果图
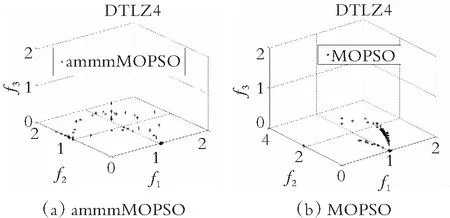
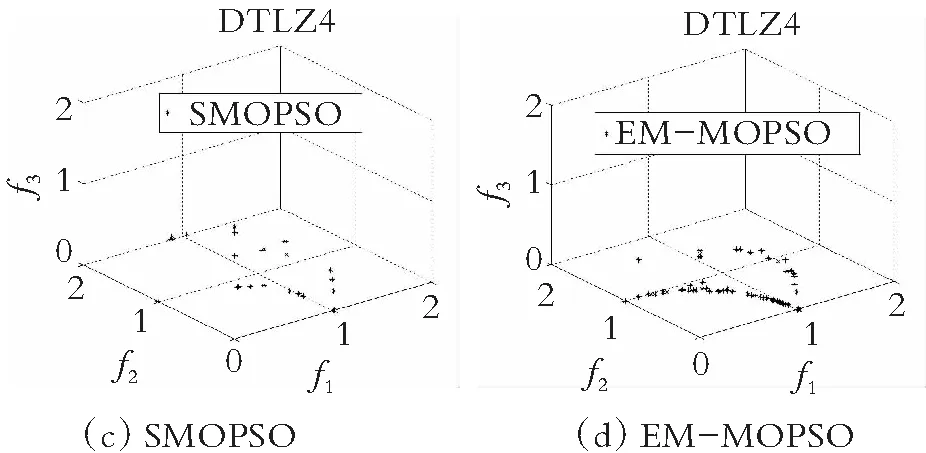
图9 对于DTLZ4函数4种不同算法的Pareto前沿效果图
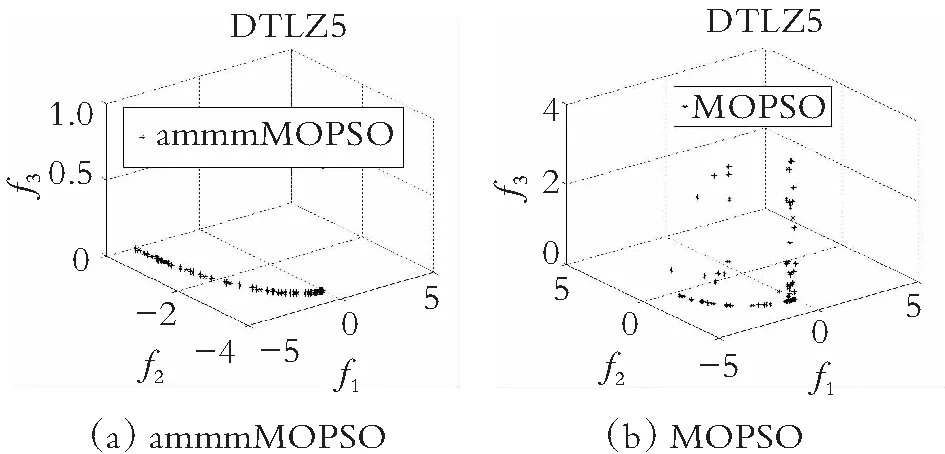
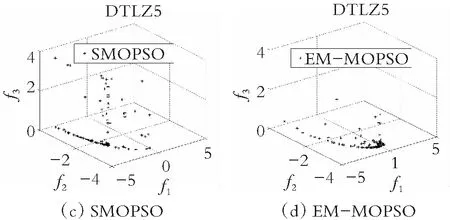
图10 对于DTLZ5函数4种不同算法的Pareto前沿效果图
为了更直观地观察各种算法在双目标测试函数ZDT1~ZDT4和三目标测试函数DTLZ2、DTLZ4和DTLZ5上的实验数据分布,图11-图12分别给出了ammmMOPSO算法和其他3种多目标粒子群算法在双目标测试函数ZDT1~ZDT4上的GD和Δ指标的箱线图,图13给出了ammmMOPSO算法和其他3种多目标粒子群算法在三目标测试函数DTLZ2、DTLZ4和DTLZ5上IH指标的箱线图,其中箱型图的横坐标1~4分别代表ammmMOPSO算法、MOPSO算法、SMOPSO算法和EMMOPSO算法。由图11可以看出,在求解这4种两目标测试函数时ammmMOPSO算法都比其他3种多目标粒子群算法有明显的优势,所获得的数据有良好的稳定性;由图12可以看出,ammmMOPSO算法Δ的波动范围都要优于其他3种多目标优化算法,说明ammmMOPSO算法所获得的数据更加稳定;由图13可知,ammmMOPSO算法的IH中值和波动范围都优于其他3种多目标算法;综上可知,ammmMOPSO算法具有较好的综合性能。
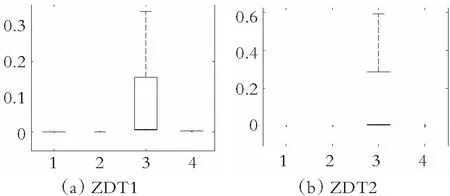
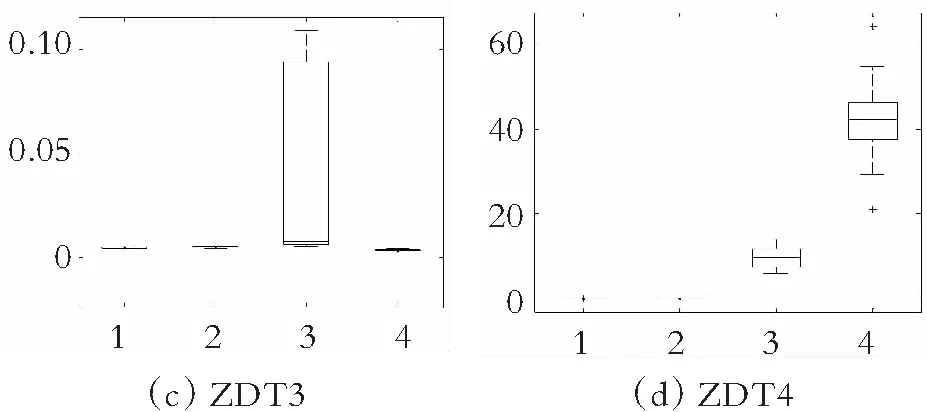
图11 GD值的盒状统计图
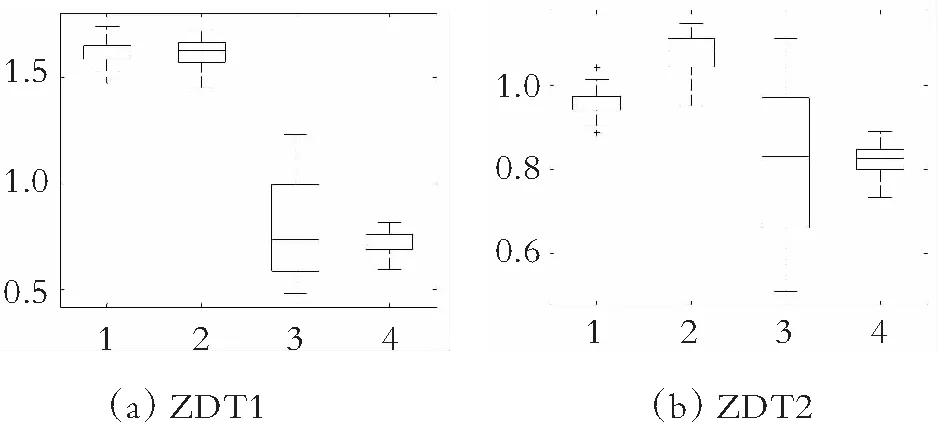
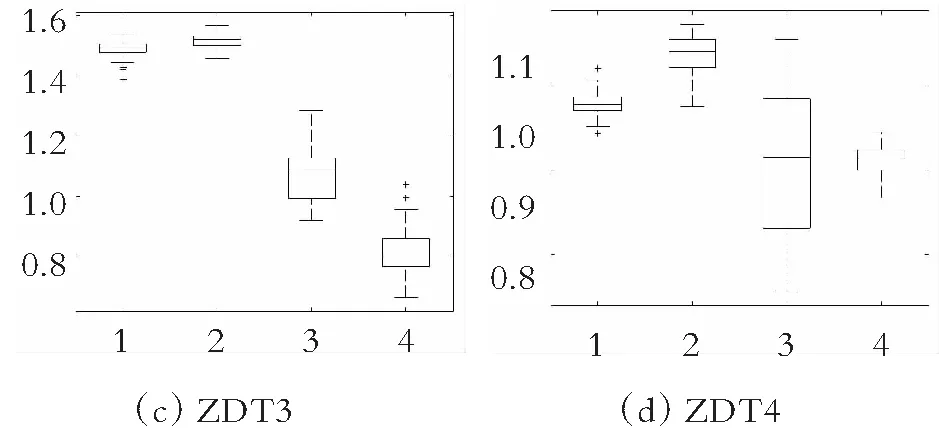
图12 Δ值的盒状统计图
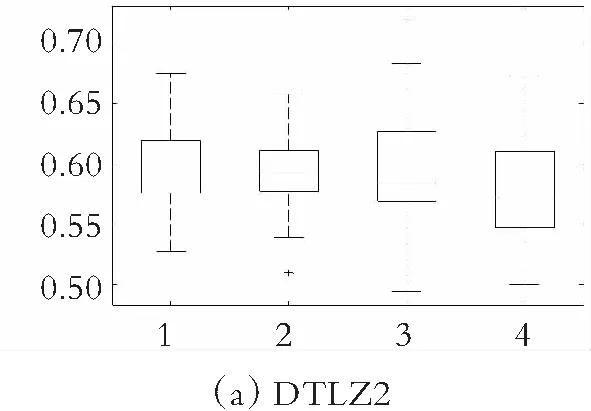
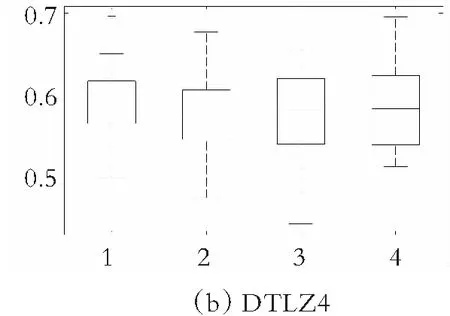
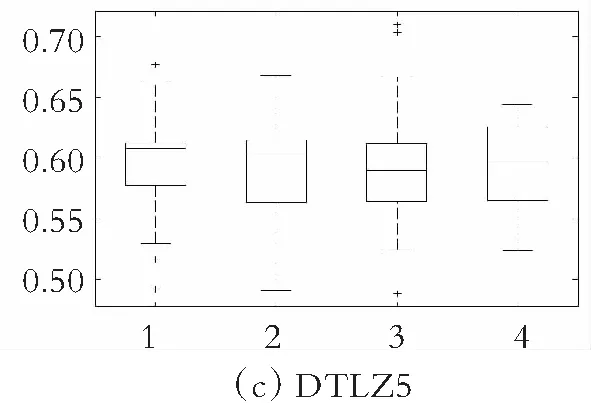
图13 IH值的盒状统计图
4 结束语
本文提出基于自适应网格混合机制的多目标粒子群算法,ammmMOPSO算法对外部存档规模的维护和全局最优样本的选取提出新的策略。在全局最优样本的选取中本文使用加权和函数策略对外部存档中的非劣解进行选取,提升了MOPSO算法的分布性和收敛性;对于外部存档的维护,本文提出相邻距离和“加权和函数”的混合策略,对密度最大的网格进行有针对地删除40%的粒子数,为选取全局最优解提供了较好的粒子质量;为了防止后期算法停滞,无法逃脱局部最优解,提出了位置的变异操作,以增强粒子的开发能力;为证实ammmMOPSO算法的有效性,ammmMOPSO算法、MOPSO算法、SMOPSO算法以及EMMOPSO算法采用双目标测试函数ZDT1~ZDT4和三目标测试函数DTLZ2、DTLZ4和DTLZ5进行仿真实验,实验仿真结果表明,ammmMOPSO算法具备较好的收敛性和分布性,且具有良好的空间化效果。

