多层线性回归方法在增值评价中的应用

杨志明 张 峰

教育评价是对教育教学活动中各种现象做出事实判断和价值判断的过程。中共中央、国务院印发《深化新时代教育评价改革总体方案》[1][2]后，“改进结果评价，强化过程评价，探索增值评价，健全综合评价”的任务变得十分突出。但是，在落实这些任务时，一线教育评价工作者往往会遇到不少挑战，其中的难题之一是缺乏实施增值评价的有效方法。已有研究表明，常用的增值评价方法有7 种[3][4]，包括增分模型（gain score model）、轨道模型（trajectory model）、分类模型（categorical model）、残差模型（residual model）、投射模型（projection model）、学生成长百分位（student growth percentile，SGP）模型，以及以多层线性回归模型（hierarchical linear model，HLM）为代表的多变量分析模型[5][6][7][8][9][10][11][12][13][14]。不过，在处理嵌套设计的数据时，只有HLM 等方法更加合理和有效。事实上，学生水平的增值幅度和速度可能与班级因素（班主任和任课教师等）有关，而班级水平又可能与学校因素有关，像这种学生数据嵌套于班级数据，班级数据又嵌套于学校数据的情形，若使用多元线性回归模型等方法实施增值评价，则很可能得出错误结论。故此，本文具体讨论多层线性回归方法及其在增值评价中的应用，以期为一线教育评价工作者处理具有嵌套特性数据的增值评价问题提供参考。

一、回归分析概述

要理解和使用多层线性回归方法，首先需要对回归分析的基本概念和线性回归方程的估计方法有所了解。

1.回归分析的目的

回归分析的目的是揭示一个现象（因变量Y）与另一个现象（自变量X）或若干个现象（自变量（X1，X2，X3，…，Xn）之间的关系，以便解释因变量的变化在多大程度上可以用自变量的变化来解释。其中，各种变量的变化通常是用其代表性样本上观测数据的方差（variance）或变异数作为指标的。因变量是随机变量，自变量一般不是随机变量。假若这种关系是线性的，则称这种回归方法为线性回归；假若这种关系是非线性的，则称这种回归为非线性回归（如多项式回归等）。对于线性回归方法而言，其基本原理是利用变量的观测数据（样本观测值），拟合所关注的因变量（Y）和影响它变化的自变量（Xi）之间的线性关系，进而实现用一个或多个自变量的变化来解释和预测另一个因变量（Y）的变化的目的。

值得说明的是，回归关系不一定是因果关系。即，回归分析中所定义的自变量和因变量并不一定是因果关系，也不是确定性的函数关系，而是概率关系，因此，回归分析中的自变量通常被称为预测变量（predictors），因变量也被称作输出变量（outcome），即Y与X所预测的估计值之间存在随机误差。

此外，回归关系也不等同于相关关系。因为回归分析中X与Y的地位不是对称的，而相关分析中二者是对称的关系；在回归分析中，X可以是随机变量，也可以不是随机变量，而相关分析中二者都必须是随机变量。

2.一元线性回归模型

要理解多层线性回归分析的方法，首先要理解一元线性回归分析。其数学模型如公式（1）所示。

其中，Yi是因变量，属于随机变量。Xi被看作是没有误差的自变量（严格地讲，Xi也是随机变量，但当Xi的随机变化与Xi的值域相比很小时，可以忽略Xi的随机变化）。β0是回归方程的截距（intercept），表示自变量为0 时Yi的值；β1是回归方程中自变量Xi的斜率，即回归系数（regression coefficient），表示自变量Xi每变化一个单位所引起的因变量Yi的改变量。β0和β1均称为模型参数。ei是回归方程中的残差项，也是随机变量，并且假定它服从均值为0、方差为σ2的正态分布。

回归分析的任务是，利用自变量和因变量在某个代表性样本上所取得的观测数据，运用某种统计方法估计回归方程的参数（β0和β1），并检验相应回归方程的有效性。一旦这个方程的有效性得到验证，则可以用这个方程解读数据样本所代表的总体（人群）上所具有的变量关系，进而用预测变量推算其因变量的值。其中，比较常用的一元线性回归方程的估计方法为最小二乘法（ordinary least squares，OLS）。

3.线性回归方程的估计方法

线性回归方程的常用估计方法为最小二乘法，其原理是：在我们将恰当的参数值（β0，β1）代入模型后，如果所有观测值与估计值之间的差值（误差）的平方和达到最小，即实现公式（2）和公式（3）中的第二项残差平方和最小，则说明模型与数据拟合良好，这时的（β0，β1）值可以作为回归方程中参数的估计值。

在得到回归方程参数的估计值后，还需要计算简单决定系数（coefficient of simple determination），如公式（6）所示。

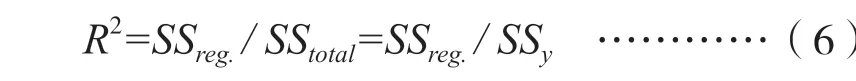
其中，R2表示因变量的总变异（方差）中有多大的比例可以用回归方程中的自变量来解释，即自变量在多大程度上解释了因变量的变化情况。在多元线性回归分析中，评价者可以通过观察决定系数的增加量（R2Change）等方法，分别估计各个自变量对因变量总方差的独立贡献。

在估计线性回归方程时，以下情况需要注意。

其次，使用最小二乘法需要满足以下条件（高斯条件假定）。

（1）因变量与自变量之间存在线性关系。

（2）模型中的随机误差项ei服从均值为0、方差为σ2的正态分布，满足方差齐性假设。否则，最小二乘法对β0的估计不是无偏估计（即当用多个样本的统计量作为总体参数的估计值时，其偏差的平均数为0）。

（3）随机误差项ei与自变量Xi独立（即两个随机变量之间的相关系数为0），它们之间的协方差为0。否则，方程中的参数估计值虽然是无偏的和一致的（当样本容量足够大时，参数的估计值会逐渐趋近于总体参数），但并非有效（有效指的是当总体参数的无偏估计不止一个统计量时，无偏估计变异小的有效性高），所得结论可能是错误的。

（4）误差项之间相互独立（即两个不同误差项之间的相关系数为0）。否则，方程中的参数估计虽然是无偏和一致的，但并非是有效的，其结论可能是错误的。不过，不满足条件（4）对非联立的回归方程组的一般单方程回归影响不大，因为X被假定为非随机变量。

此外，变量Y与X之间必须是交叉关系，而不是嵌套关系。否则，不符合高斯条件假定，会得到错误的参数估计值。例如，假定有一个研究探讨学生学习动机（Y）与其数学成绩（X1）和语文成绩（X2）的关系，这3 个变量间的关系就属于交叉关系（cross design），对这种数据可以做二元线性回归分析，其方程如公式（7）所示。

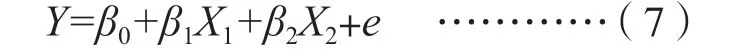
若把第i个人的观测数据代入公式（7），则回归方程可变为公式（8）形式。

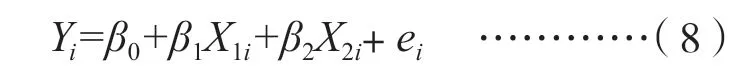
假若本研究还涉及第4 个变量，如教师水平（W1），则Y与X1，X2之间的关系仍然是交叉关系，它们可以实施简单的多元线性回归分析。但这3个变量与教师水平（W1）是嵌套关系（同一个班的教师水平是同一个值，误差不是随机的，违反高斯条件），所以不能把W1作为直接影响变量Y的自变量进行多元线性回归分析。也就是说，不能用方程（9）来实施多元线性回归分析。

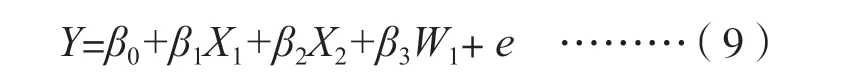
这是因为教师水平或其他条件不同使得每一个班都有一条不同的回归线。W1是一个调节变量，即学生学习动机（Y）与数学成绩（X1）、语文成绩（X2）的关系，取决于教师的水平（W1）。教师水平不同，这3 个变量之间的关系会有所不同。要解决这类问题，就需要使用多层线性回归方法。

二、多层线性回归方法

1.数学模型

多层线性回归方法主要用来处理数据中出现嵌套关系时的回归分析问题。典型的嵌套设计常常出现在班级层面、学校层面或区域层面的教育评价工作中，进而应用在增值评价之中。例如，假定有人要研究学生的学习动机（Y）受到数学成绩（X）影响的“规律”，可以直接建立一元线性回归模型。其数据结构如表1 所示。

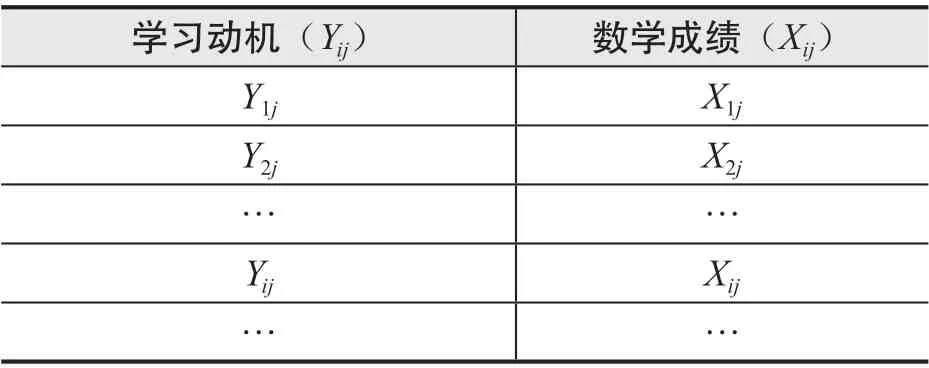
表1 学习动机与数学成绩的观测数据

由于这种关系受到“教师”水平（W）的影响，因此，每个班都有一条不同的回归方程。于是，可以建立第一层次的回归方程，如公式（10）所示。

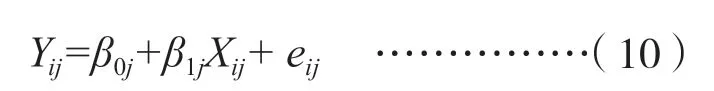
其中，Yij表示第j班第i个学生的学习动机指数，Xij表示第j班第i个学生的数学成绩，i代表任意一个学生，j代表任意一个班级。由于每个班级的教师水平不同，所以每个班会有不同的回归方程，其回归方程的参数与教师变量的关系如表2 所示。

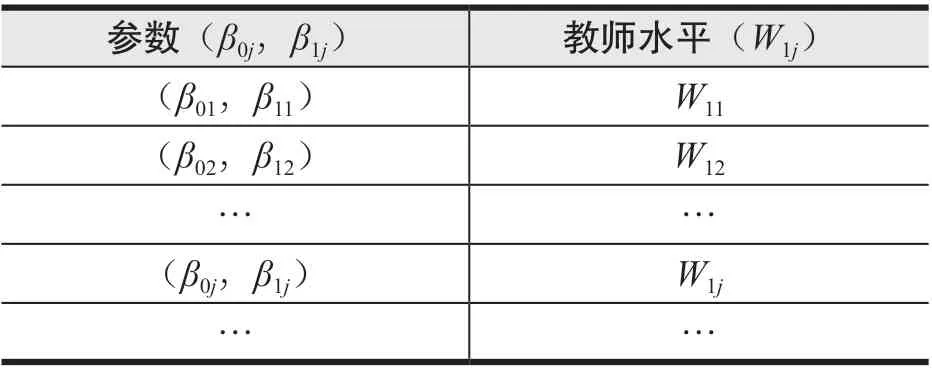
表2 每个班的回归方程参数与教师变量之间的关系

换句话说，若把第一层回归方程中的参数看作随机变量（每个班级都有不同的参数，参与研究的所有班级可以看作是从班级总体中随机抽取的一个样本），则可以由表2 中第一层回归方程中的参数（β0j，β1j）分别建立一个对教师（W1j）的回归方程。得到的第2 层次的回归方程如公式（11）和公式（12）所示。

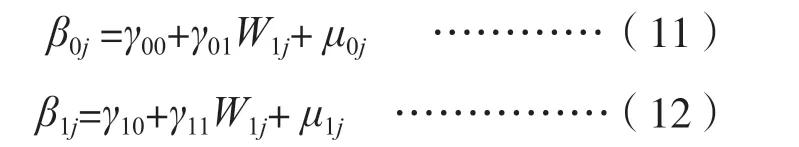
其中，γ00是所有班级第一层回归方程中截距β0j的均值，γ10是所有班级第一层回归方程中预测变量斜率β1j的均值，μ0j和μ1j是第二层回归方程中的随机误差项，分别服从均值为0、方差为var（μ0j）=τ00和var （μ1j）=τ11的正态分布。

具体地，斜率β1j反映的是X与Y的关系，第2 层变量W的作用是加强这种关系（两个层次回归系数符号相同），或减弱这种关系（两个层次回归系数符号相反）。若β1j对W1j的回归不显著，则表明X与Y的关系不因教师水平的不同而不同，但不是X与Y之间没有关系。β0j指的是在第j班教师的影响下，全班学生（中心化以后）的数学成绩与学习动机关系程度的平均水平，τ00是用W1j解释了第一层回归方程截距β0j的变异之后第2 层回归方程的残余方差，τ11是用W1j解释了第一层回归系数β1j的变异之后第2 层回归方程的残余方差。

值得再次强调的是，多层线性回归与多元线性回归具有本质的区别。若将第2 层回归方程公式（11）和公式（12）代入第1 层回归方程公式（10），则有：

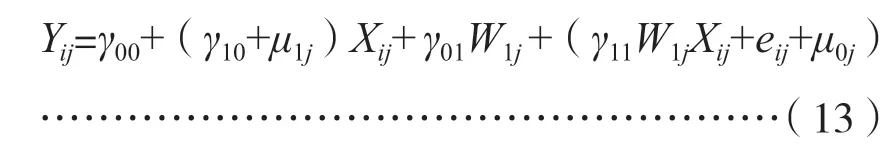
这似乎与多元线性回归Y=β0+β1X1+β2W1+e是一样的，但二者的性质是不同的。因为其中的误差项包含（非线性的）交互效应项γ11W1jXij项，违反了高斯条件，这时用最小二乘法来估计参数会造成错误。事实上，在多层线性回归模型中，回归系数β0j和β1j是随机变量，而不是普通线性回归中的常数，它们被进一步分解成了一个常数γ00（或γ10）与随机数μ0j（或μ1j）之和。

使用多层线性回归模型的前提假设包括：（1）残差项eij服从均值为0、方差为σ2的正态分布，任何两个eij之间相互独立；（2）cov（μ0j，eij）= cov（μ1j，eij）=0，cov（μ0j，μ1j）=0，j1≠j2（任何残差项之间协方差为0）。

2.实施步骤

在实施多层线性回归时，一般需要经历建立虚无模型、根据虚无模型结果逐步添加高层次预测变量建立多种研究模型等多个步骤。

步骤1：建立虚无模型，即检验不加入任何预测变量的Null Model 或0 模型。其常见形式如公式（14）和公式（15）所示。

公式（16）等价于单因素方差分析模型。其中，γ00是因变量的总均值，μ0j是组间效应（班级之间变异数SSb），eij是组内效应（全体学生得分变异数SSw）。于是有：

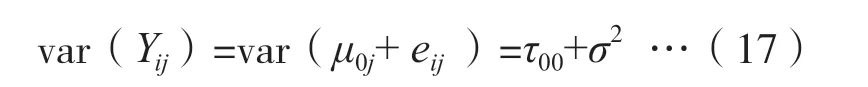
这一步的目的是考察第一层和第二层的随机误差项的变异数是否足够大（用χ2检验），以决定是否需要引入其他预测变量。其方法类似于多元线性回归中逐步加入预测变量的办法，其判断标准是决定系数的增加量（R2Change）是否有意义。

步骤2：建立研究模型，即第一层的模型公式（10）以及第二层的模型公式（11）和公式（12）。

其中，τ00是同一组（班级）内学生之间的协方差，即，

建立该模型的作用在于确定是否要引入第2层变量（如教师水平W）来解释第1 层回归方程中的模型参数。这时一般希望τ00和τ11之中至少有一个值足够大。其判断准则如下：

（1）当τ00足够大时（p＜0.05），说明有必要引入第2 层次的预测变量来解释第1 层次中的截距β0j变异。至于新引入的水平2 的变量能否有效地解释水平1 的截距变异，则要看第2 层次回归系数是否显著（p＜0.05）。若τ00变异数未达到显著水平，则可以令第二层的模式为固定模式β0j=γ00。

（2）当τ11足够大时（p＜0.05），说明有必要引入第2 层次的预测变量来解释第1 层次中的斜率β1j变异。至于新引入的水平2 的变量能否有效地解释水平1 的斜率变异，则要看第2 层次回归系数是否显著（p＜0.05）。若τ11变异未达到显著水平，则可以令第二层的模式为固定模式β1j=γ10。

（3）在回归系数不显著时，也可以考虑非线性回归（如用全模式中W2作为预测变量等）的方法。

（4）在实施多层线性回归分析时，需要对各组（班级）之间的方差做齐性检验，即对各组间最大方差与最小方差之比做F检验。

为了确认是否需要引入第二层次的预测变量，也可以计算组内相关系数（intra-class correlation），即同一个组内（如班级）学生之间的相关系数，如公式（20）所示。

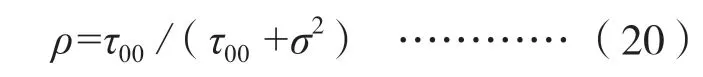
该指标反映在因变量Y的总变异中有多大比例来自第2 层变量（组间变异）。若经过χ2检验发现差异显著，则说明有必要加入第2 层变量进行多层次分析。其价值类似于多元线性回归分析中的R2Change，但ρ不是指自变量所能解释因变量变异的百分比，其作用在于判定是否值得在第2 层回归分析中加入预测变量。当然，是否需要引入第2 层预测变量，不能仅仅局限在数据分析本身，还需要考虑相关的理论和实证研究成果。

三、多层线性回归方法在增值评价中的应用

在关于学生语文水平发展的追踪研究中，笔者收集了学生3 年共6 次语文期末测试成绩，旨在探究学生的语文水平在初中阶段的增值情况。

1.研究假设

这里的研究假设是学生的语文水平会随着时间的推移而增长，但这种增长幅度和速度会受到授课语言和性别的影响。具体的研究问题是：（1）学生语文水平在初中阶段的增长幅度和速度如何？（2）学生语文水平的增长与性别的关系如何？（3）学生语文水平的增长与授课语言的关系如何？

2.研究对象

参加本项研究的学生来自粤语地区4 所初中学校的21 个班，共698 人参与测试。其中，实验组包括11 个班，共354 人，对照组包括10 个班，共344 人，每个班的男女学生比例均衡。

3.实验过程

实验组选用普通话作为授课语言，对照组选用广东话作为授课语言。语文水平的衡量指标为专门的语文测试成绩，包括词汇、句式、交际用语、称谓用语、叹词、阅读理解、改写句子、作文，共8 个部分。每次施测时间为每个学期期末，3 年共收集了学生的6 次测试成绩。

4.研究方法

在本项研究中，学生的语文成绩（因变量Y）受制于两个层次的自变量影响。第一层为时间变量（T），第二层为学生变量，包括性别（女1，男0）和组别（实验组1，对照组0）。由于第1层数据嵌套于第2 层数据之中，所以本研究采用了多层线性回归方法。

本文仅以词汇测试成绩（因变量Y）为例进行讨论，自变量为时间（T，水平1）、性别（W1，水平2）和组别（W2，水平2）。根据数据特点和虚无模型的分析结果，本次统计分析选用了3个模型，分析软件为多层线性回归模型的专用软件MLwiN[15][16]，其运算代码如下：

模型1：虚无模型（第2 层不含预测变量）

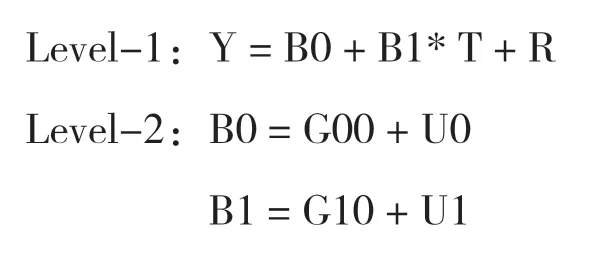
5.结果与讨论

经过多层线性回归模型软件分析，本研究分别得到固定效应模型和随机效应模型的结果，如表3 和表4 所示。

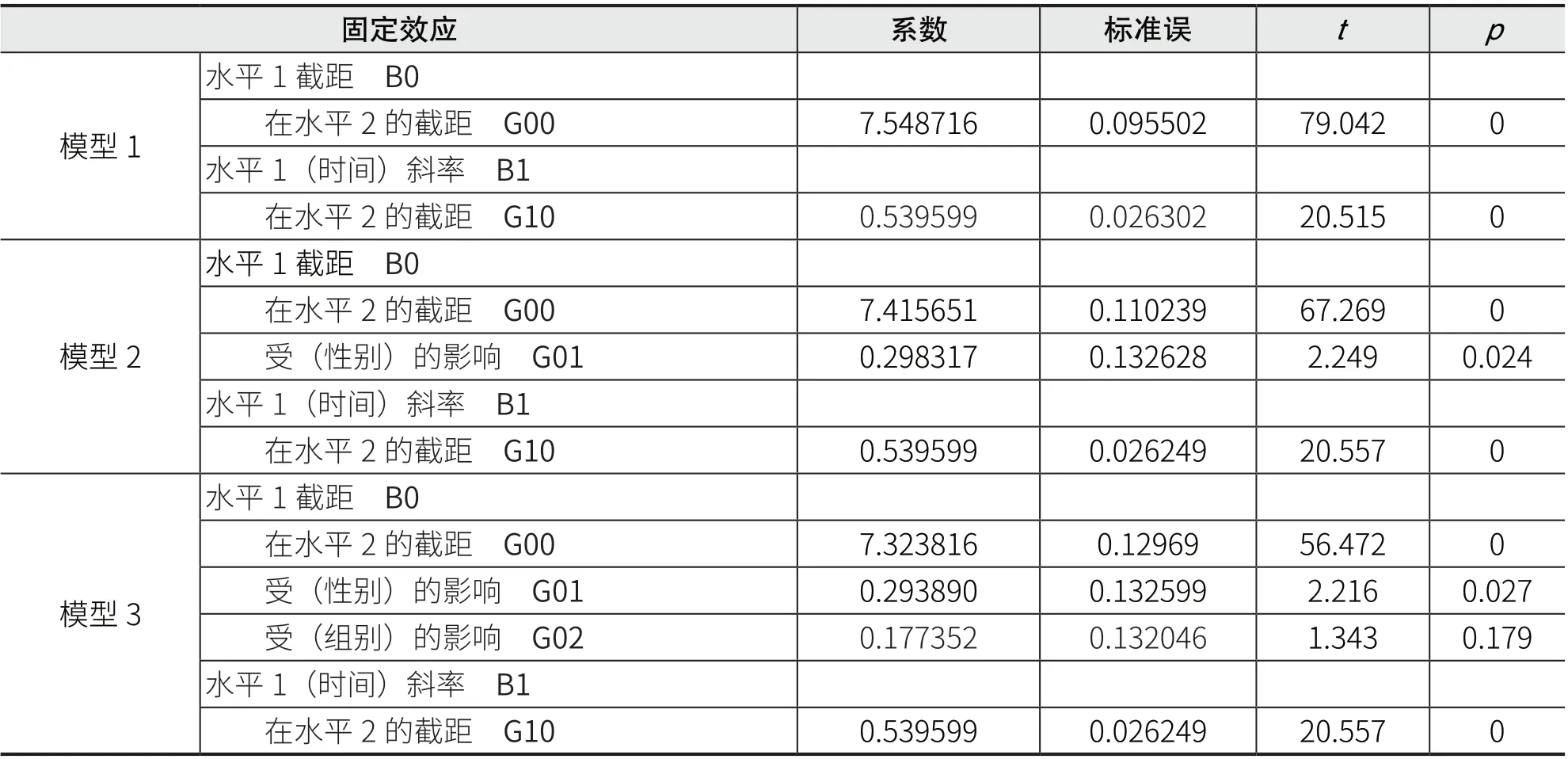
表3 固定效应模型多层线性回归分析的结果

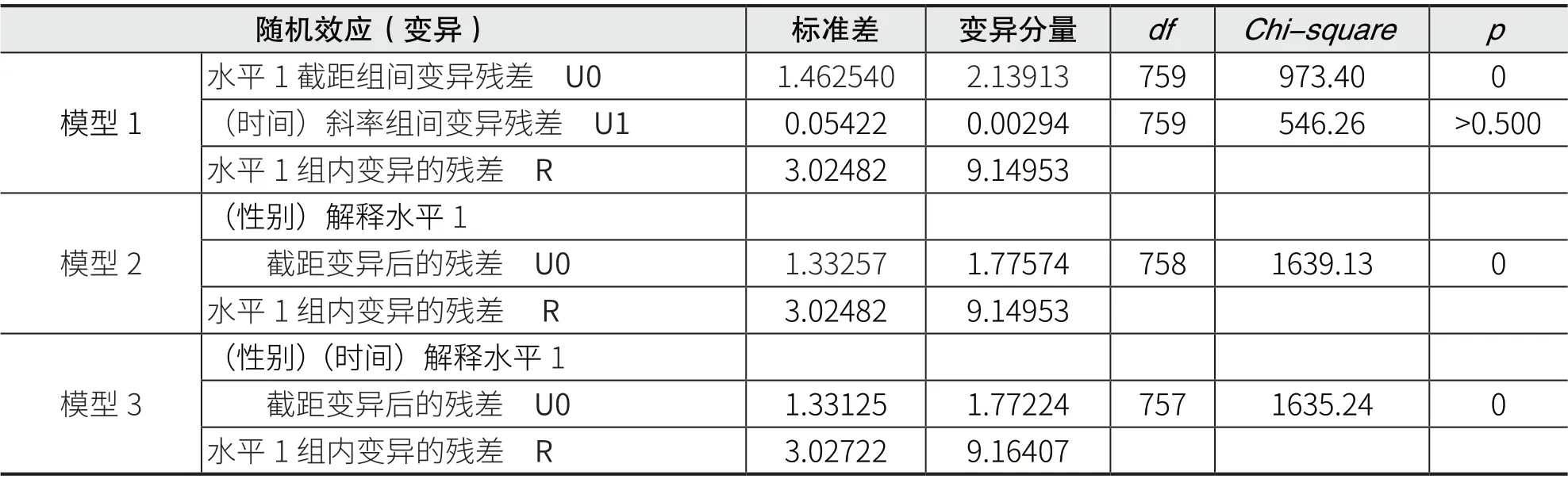
表4 随机效应模型多层线性回归分析的结果

首先，考察学生词汇水平是否随时间推移而提高，以及是否有必要引入第2 水平（学生水平）变量。以时间T为自变量，学生成绩Y为因变量，建立简单线性回归模型（模型1）。由表3模型1 的结果可知，学生成绩对时间变量的回归系数达到了非常显著的水平（p＜0.01），说明学生的成绩随着时间的推移而有非常显著的增值。（由于时间编码为-5，-4，-3，-2，-1 和0，所以最后模型中水平1 的截距是学生现今成绩的反映，以下讨论均同此设定）

另外，由于只有截距变异的残差（U0=2.13913，见表4）非常显著地不为0（p＜0.01），斜率变异的残差没有达到显著不为0 的水平（p＞0.500），因此，只需要引入预测水平1 截距的第2 水平变量（性别和组别），水平1 的斜率效应可以作为固定效应来处理。

其次，对学生变量（性别）效果进行分析。由表3 中模型3 的结果可知，水平1 截距对性别变量的回归系数达到了显著水平（p=0.027＜0.05），说明性别因素对学生成绩有显著的影响。又因为回归系数（0.293890）大于0，女生编码为1，男生编码为0，所以女生发展水平优于男生。

另外，引入性别变量后，尽管截距变异的残差由2.13913 减少至1.77574（表4），但新的残差仍然非常显著地不为0（p＜0.01），因此，有必要再次引入新的第2 水平预测变量。

最后，对学生变量（组别）效果进行分析。由表3 中模型3 的结果可知，水平1 截距对组别变量的回归系数没有达到显著水平（p=0.179＞0.05），这就说明新引入的组别变量也不能较好地解释截距变异中的残差变异。也就是说，组别变量对学生水平的影响没有达到显著的水平。

6.结论

由上述分析可知：（1）学生的词汇成绩会随着时间的推移而有非常显著的提高（p＜0.01），即学生的语文词汇水平在初中阶段实现了非常显著的增值；（2）性别因素只会对学生成绩的增幅产生显著的影响（女生优于男生，p＜0.01），对学生成绩提升速度的影响却没有达到显著水平（p＞0.05）；（3）选用普通话授课或使用广东话授课，对学生现今的词汇成绩以及成绩的变化速度都没有显著影响（p＞0.05）。

总之，多层线性回归方法在处理嵌套数据的增值评价问题时，对结果的分析更为合理，效果更好。参照本文所提供的解读和案例，可以为增值评价的实施提供新的思路。