利用循环网络的降落伞开伞载荷补偿方法*
姜 添,李 健,戈嗣诚
(北京空间机电研究所, 北京 100094)
降落伞技术是飞行器进入、下降和着陆[1](Entry, Descent, and Landing,EDL)关键技术的核心部分,降落伞的典型工作过程包括伞系拉直、充气展开、稳定减速三个阶段。其中伞衣的充气展开最为重要,该过程的研究关注点主要面向伞的载荷变化和应力分布、伞衣变形和阻力面积等,工程应用及科学探索对该阶段的常用研究手段包括以下三种:完全试验法、数值模拟法与半理论半试验法。其中,完全试验法一般用风洞实验[2]或空投试验[3]等方式直接获取伞的相关数据,准备周期长、试验成本高,适用于理论研究与产品的初样验证,工程设计阶段已很少采用;数值模拟法多以任意拉格朗日-欧拉法[4](Arbitrary Lagrange-Eulerian method,ALE)以及变空间域/稳定时间-空间法[5](Deforming-Spatial-Domain / Stabilized Space-Time, DSD/SST)等计算机仿真方法处理物伞系统的流固耦合问题,并在实践中有所应用[6-7],但受限于技术能力,数值模拟法目前难以满足产品初步设计过程中计算简单、快速应用的需求;为了对一些典型应用工况进行快速、准确的计算分析,有学者结合大量的伞系试验总结出应用于物伞系统的经验公式[8],而后发展成为半理论半试验法,这类方法可以让研究人员迅速获取给定条件下的开伞力及飞行速度等重要参数的预测数值并据此判断伞的性能状态是否满足设计要求,是工程中常用和高效的方法,不足之处是具有非常强的经验参数依赖性和应用场景局限性,很多学者针对此问题对经验公式进行了改进与优化[9-10],但仍存在较大的提升空间。近年来快速发展的机器学习理论凭借其强大的非线性拟合与泛化性能受到了部分研究者的关注,进行传统方法结合机器学习的学科交叉研究可以为提高经验公式模型的精度与适用性提供一种新的研究思路。
由于机器学习的细分种类繁杂,选择合适的模型对提升训练的效率与准确性大有裨益。考虑空投试验中飞行器与降落伞的飞行状态变化,将空投过程在时间维度上进行离散,可以认为:物伞系统每一时刻的飞行状态与前一时刻或几个时刻的状态量密切相关;与较远时刻状态的相关性较小;与后续时刻状态无关。这种以时间序列为基础的数据特性尤其适用于循环神经网络(Recurrent Neural Networks,RNN)模型[11],该类网络与其变种——长短时记忆网络[12](Long Short-Term Memory,LSTM)目前在处理序列问题中表现出较大优势,并广泛应用于互联网中的自然语言处理相关领域,在部分非互联网行业中也有涉猎[13-15]。而在降落伞的相关行业中,国内外使用机器学习方法进行研究的参考案例较少,且大部分限于对伞绸透气性[16]及伞衣织物强度[17]的研究,对展开过程中载荷特性等问题的探索有限,循环网络与降落伞的交叉应用具有很大的挖掘空间。
本文针对开伞过程中开伞力的预测,提出了一种使用循环网络结合经验公式的补偿计算模型,包括模型架构的详细设计以及对训练集与测试集的数据预处理方法等。使用3种不同的网络模型对开伞力的仿真结果进行比较分析并探索循环网络中超参数对训练结果的影响,给出本模型的最优训练参数。
1 充气时间理论
半理论半试验法中常用的计算方法有充气距离法与充气时间法,二者由动量方程的自变量不同进行区分,本文使用的是以充气时间作为自变量的充气时间法。
降落伞与回收物在开伞过程中的平面受力情况如图 1所示。建立该系统运动方程时,首先给定以下假设条件:①该运动为双质点运动,伞质心位于伞衣底边中心且相对底边位置不发生变化;②忽略物伞系统升力;③物伞轴线始终重合;④忽略伞绳弹性,物伞相对位置不发生变化。
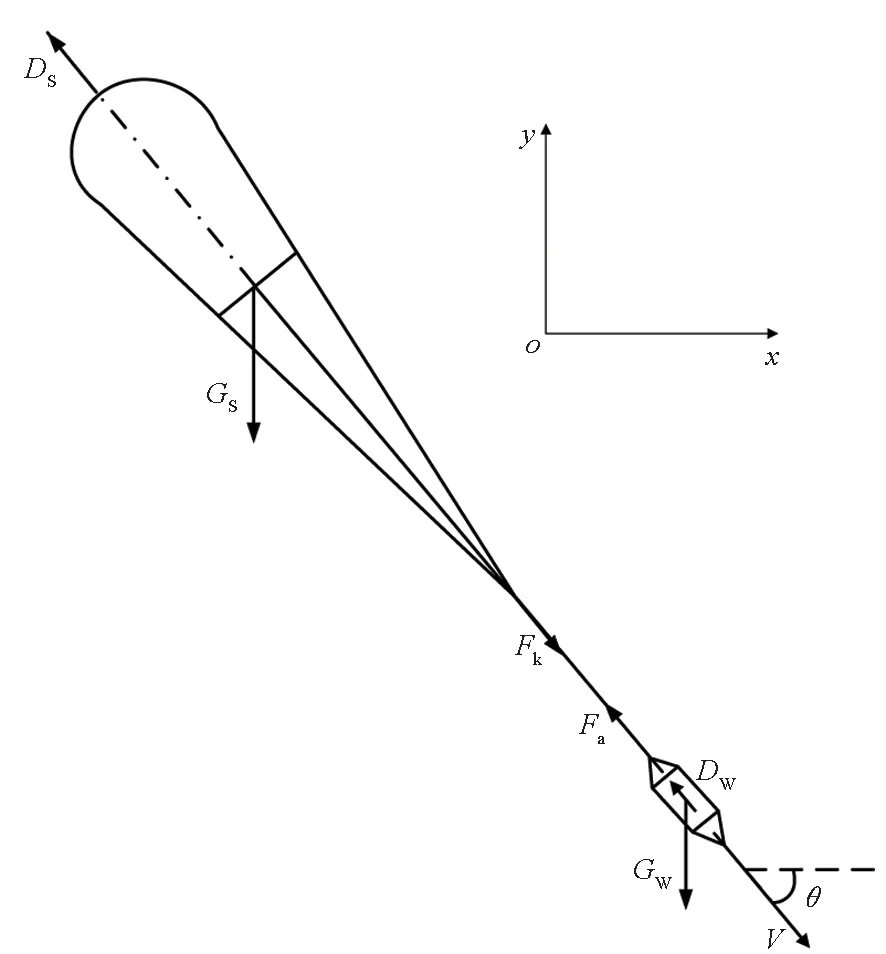
图1 平面物伞系统力学模型Fig.1 Mechanical model of object-parachute system
在上述假设条件的前提下,可建立物伞系统合速度V关于时间t的微分方程以及降落伞拉力Fk的表达式:
(1)
(2)
其中:θ为物伞系统轴线与水平方向夹角;mw为回收物质量;ms为降落伞质量;mf为附加质量,
mf=ρkfC1.5
(3)
C表示降落伞的瞬时阻力特征,
(4)
式中,tm1表示初始充气时间,tm表示充满时间,且各参数满足关系式:
(5)
式(1)~(5)中其余物理量及参数含义为:D0表示伞衣名义直径,VL表示拉直速度,C1表示初始充气时期的伞衣阻力特征,Cs表示充满伞衣的阻力特征,Cw表示回收物的阻力特征;kf表示附加质量系数,λ1是与伞型有关的常数,λ2是与伞衣透气性有关的常数,指数p在充气时间法中通常取1~5。
上述系数和常数为经验参数,是充气时间理论的核心部分,一般通过大量试验测试综合总结获得。
2 循环神经网络
循环网络相当于是以时间顺序串联的前馈网络(Feedforward Neural Networks, FNN),其模型原理和隐层细胞结构如图 2所示。标准3层RNN结构下t时刻网络的前向传播过程可由下列公式计算:
(6)
式中:x(t)、h(t)、y(t)分别表示输入向量、隐层向量与输出向量;U、V、W分别表示输入与隐层、隐层与输出层、隐层与隐层之间的权重参数;b和c分别表示隐层与输出层神经元的阈值;σ为sigmoid函数。
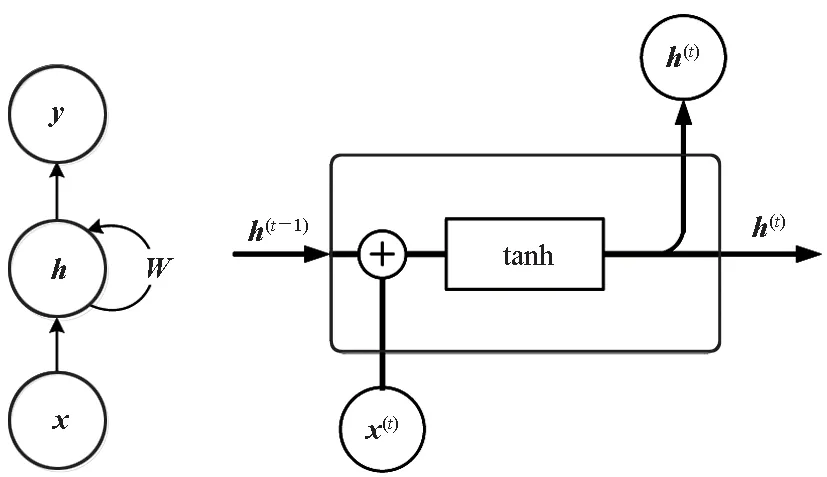
图2 RNN模型及其隐层细胞结构Fig.2 RNN model and cell structure of hidden layer
标准RNN模型的缺点是时间序列过长时,训练梯度会趋向于消失或者爆炸,该现象被称为循环网络的长期依赖挑战。为了缓解这一问题,近年来学者们研究了RNN的多种变体,其中的LSTM模型较为有效,其隐层细胞结构如图3所示。
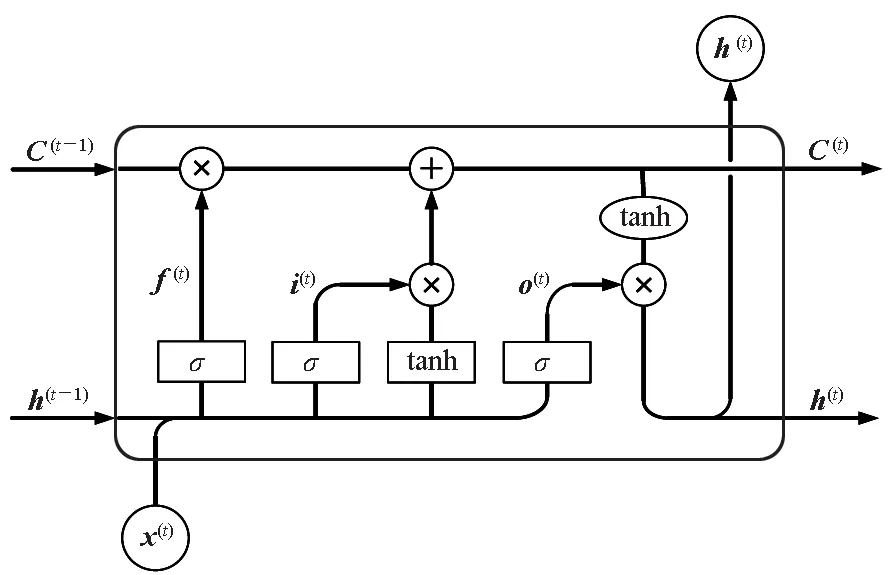
图3 LSTM细胞结构Fig.3 Cell structure of LSTM
LSTM具有内部的循环(自环)结构,引入了状态单元C与“门控”的概念,包括输入门、遗忘门和输出门。新结构的加入使LSTM对细胞内部信息的处理变得更加细化,信息的存储与更新也更有效率,训练过程不再是简单的输入量与循环单元之间的仿射变换。相较RNN,LSTM的网络复杂度与网络性能均有所上升,其前向传播公式为:
(7)
式中:f、i、C、o分别表示遗忘门、输入门、状态单元和输出门,h、y表示当前隐层向量与输出向量,b、U、W表示对应门控的阈值、输入连接权重和隐层连接权重,σ为sigmoid函数,⊙表示向量积运算。
训练数据需通过Min-max标准化方法处理后,使用基于时间的反向传播算法(Back Propagation Through Time,BPTT)结合批梯度下降法(Batch Gradient Descent, BGD)进行训练,其中批尺寸B取100。
3 开伞载荷补偿方法
3.1 开伞载荷补偿模型原理
本文所使用的基于充气时间法的经验公式已经具备一定的工程应用价值,开伞载荷补偿模型的原理是将基于该经验公式的理论拉力计算值代入循环网络进行训练,其目的是将理论值向试验真值进行补偿,并获取成熟的网络训练结果,使补偿后的载荷计算值更加接近试验真值,以此提高最终结果的预测精度。
考虑所能够使用的有效数据量和数据特征,并满足循环神经网络的应用能力,构建开伞载荷补偿计算模型框架如图 4所示,该框架主要包括经验公式、网络训练和输出预测三个功能模块。该模型的运行思路如下:①利用经验公式初步获得某工况条件下开伞过程中的开伞力预测初值;②将预测值经过数据预处理,获得可以进行网络训练的输入特征向量;③选用相应的网络模型进行训练;④训练集的网络输出参与反向传播更新网络权重,测试集的网络输出经过反标准化方法获得补偿后的开伞力输出值。
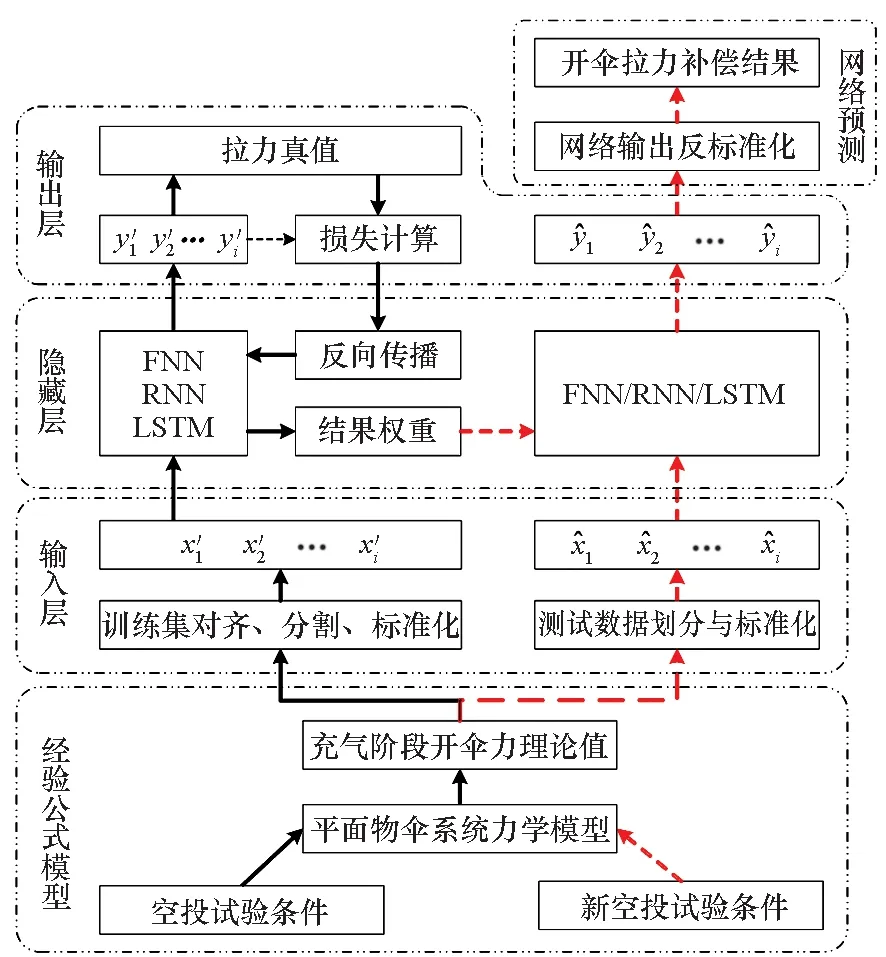
图4 开伞载荷补偿模型框架Fig.4 Compensation model framework of parachute deployment load
3.2 数据预处理
3.2.1 训练数据获取
试验数据来源于4种条件下的低空开伞空投试验:配重质量为6 040 kg,降落伞伞型为盘-缝-带伞,伞名义面积为200 m2,设计无限质量开伞方式。试验过程中使用拉力传感器同时采集时间与拉力信号,采样频率为2 kHz,同时搭配GPS接收机采集其他试验数据。经验公式法的初始条件由空投试验要求给定,气象条件使用当地月平均气象数据或探空气球实测数据。
本文的主要研究对象是伞充气阶段的开伞力变化,对开伞过程中伞系拉直至载荷峰值时间和开伞载荷均进行了统一的标准化处理,如图 5所示,具体数据处理方式如下:
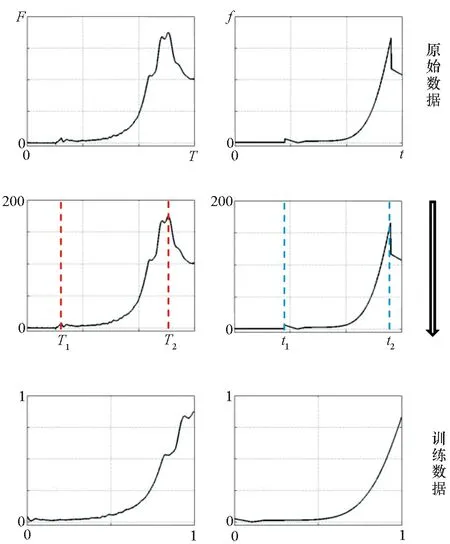
(a) 开伞力真值(a) Truth force (b) 公式计算值(b) Calculated value 图5 开伞力数据处理过程Fig.5 Parachute deployment data processing
1)对空投试验拉力及经验公式计算拉力进行有效数据截取,选取区间固定为伞系拉直时刻至拉力峰值时刻;
2)通过插值方法将上述区间内的拉力数据统一规范至相同维度,本文选取的数据维度为4 000,即单次试验参与网络训练的有效数据有4 000个;
3)将所有拉力数据采用Min-max标准化方法进行归一化处理,数据序列上下限选取为(0,200)。
经过上述步骤处理的拉力数据在时间与量级两个方面实现了归一化,以经验公式法的计算值作为网络输入、以空投试验数据作为目标值参与网络训练。
3.2.2 样本划分与验证方法
为了满足网络训练要求与样本数据量,需要对归一化的数据进行分割,以获取训练集的输入向量与目标向量。由上节可知,单次空投条件下由经验公式产生的训练样本及对应真值为:
(8)
设循环网络输入向量维度为n,输出向量维度为m,时间维度为τ,从x1开始顺序选取连续n个数据构成单一时刻内的输入,同理,从y1顺序选取连续m个数据作为对应的目标向量,则第i组向量的表达式为:
(9)
式中,1≤i≤4 000-[max(n,m)-1]。
再从x1和y1开始分别顺序选取τ个向量构成满足时间维度的网络输入与目标矩阵:
(10)
式中,1≤i≤4 002-max(n,m)-τ。
由x′i、y′i组成对应数组di=[x′i,y′i],将di代入网络即是完成对RNN/LSTM的一次训练,遍历所有样本视为完成一次循环。由此可以得到一组试验数据产生的训练样本:
(11)
式中,1≤i≤4 002-max(n,m)-τ。
本文共使用了4组空投试验数据,选取其中3组用作网络训练,共产生样本d1、d2、d3,将所有样本进行混合,然后再乱序排列,即可得到训练集总样本:
{d|d=(di)}
(12)
式中:1≤i≤3×[4 002-max(n,m)-τ]。
验证集数据的处理相对简单,将未参与训练的1组数据用作结果验证,首先按照上述方法获得d4,代入网络计算并获得输出矩阵,其形式为:
(13)
式中,1≤i≤4 002-max(n,m)-τ。
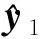
(14)
式中,2≤k≤4 000-[max(n,m)-1]。
使用该方式的目的:一是为了尽量减小验证过程中初始随机隐层的影响;二是考虑到循环网络的计算特点,过去时刻的数据会对当前时刻的样本预测结果产生影响,该种数据处理的形式可以提高样本的利用率。
4 仿真结果分析
4.1 开伞载荷补偿结果
使用FNN、RNN与LSTM三种网络结构进行实验。其中FNN为5层结构,包括输入层、3层全连接隐藏层、输出层,每层神经元个数均为4 000,与输入层维度相同,网络信息遗失率(Dropout)取0.5。经过前期试错,FNN采用的训练方案是以整体经验公式计算结果作为输入,以整体空投真值作为目标值,该方法在网络层数为3层和4层时无法收敛,在5层结构下可以获得有效结果。RNN和LSTM模型则是使用3.2节介绍的数据处理方式与训练方法,二者均采用输入层—隐藏层—输出层的3层结构,网络输入维度n=10,隐层维度h=6,输出维度m=1,学习率η=0.05,时间序列τRNN=50、τLSTM=100。图 6给出了验证集数据经过不同模型进行补偿后的拉力变化曲线。
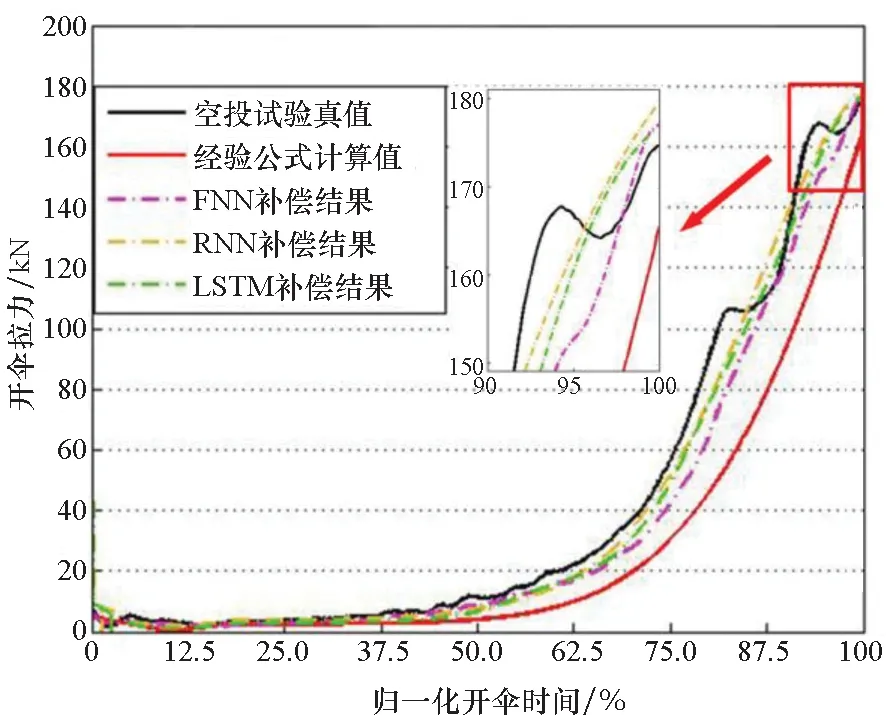
图6 补偿模型的拟合结果Fig.6 Fitting result with compensation model
从图 6可以看出,在载荷曲线的比较中,总体上看三种补偿结果均能正确地反映拉力变化趋势,相较经验公式计算的开伞力,补偿后计算值更加贴合试验真值;在开伞力峰值的比较中,补偿值与真值之间的相对误差明显缩小,但是FNN的补偿结果整体低于循环网络;在实验方法的比较中,两种循环网络的计算结果相近,且均优于FNN。
图 7给出了各模型的归一化载荷绝对误差变化曲线。由图可知,经验公式计算值在前40%的时间内与真值的绝对误差小于0.02,之后二者的误差迅速攀升,FNN模型约在60%的时刻后才出现误差的明显增长,RNN与LSTM则将该时间点向后推延至70%,这些曲线分歧点的延后可以说明模型仿真能力的增强,保证了拟合结果在分歧点前与试验真值的一致性。
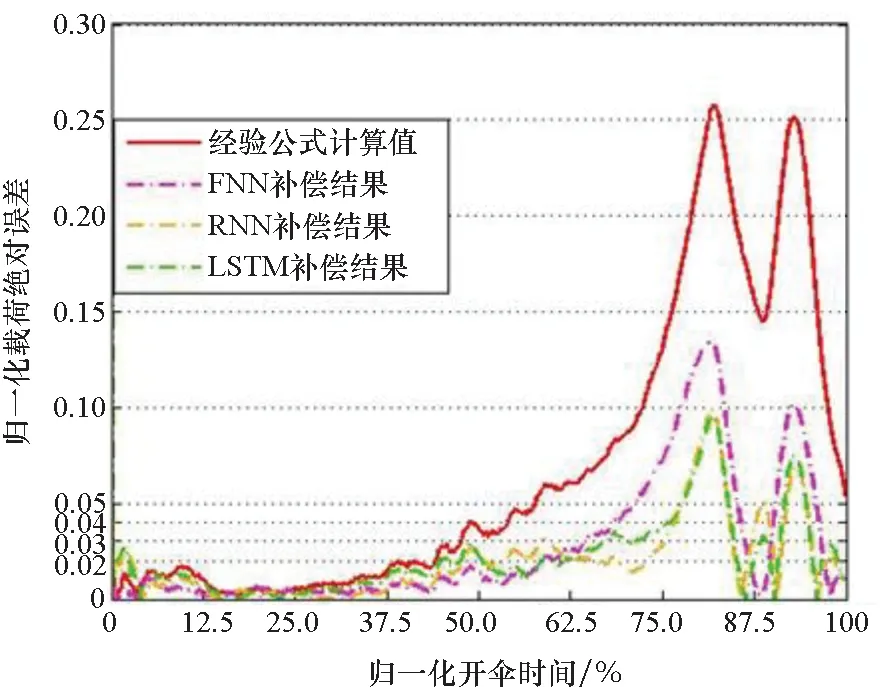
图7 多模型归一化载荷绝对误差变化曲线Fig.7 Normalized load absolute error of multiple compensation models
各种拟合模型与真值的误差出现较大增长的主要因素是未能反映出图 6空投试验数据的拉力平台期现象,基于经验公式的网络补偿方法在结果上表现出的数据规律仍与经验公式较为相似。文献[18]中利用RNN以同源数据的不同方案拟合出的载荷曲线可以展示出该拉力波动,表明循环网络具有训练出盘-缝-带伞充气展开过程中拉力波动的能力,说明本文实验的预测结果存在过拟合的成分,补偿模型与训练方式仍有改进的空间;文中使用的3组训练样本相较其他机器学习案例来说仍然是偏少的,3.2.2节的数据预处理过程即是针对循环网络样本不足问题所采取的数据增强手段,以求在一定程度上弥补数据量缺失的弱势。本实验中的样本数据相对有限且训练特征较为单一,结果容易存在过拟合,这样的情况在FNN中更为突出,这也是FNN训练结果不如RNN与LSTM的因素之一。
4.2 网络超参数影响分析
除此之外,本文比较了学习率、输入层维度、隐层维度等超参数对网络性能的影响。超参数是在开始进行训练之前设置的参数值,不是通过训练得到的参数,神经网络的训练目的之一是对超参数进行优化而提高网络的学习性能。
图8给出了不同学习率下三种网络的峰值误差与均方误差的变化情况,具体数据如表1所示,训练条件与图6所示案例相同。
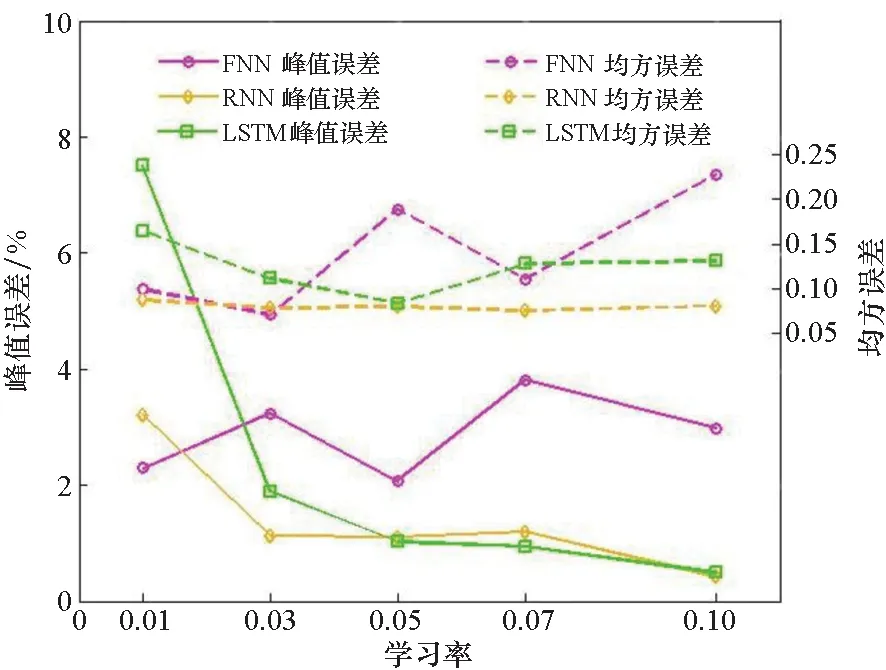
图8 不同学习率的模型精度对比Fig.8 Comparison of model accuracy with different learning rate
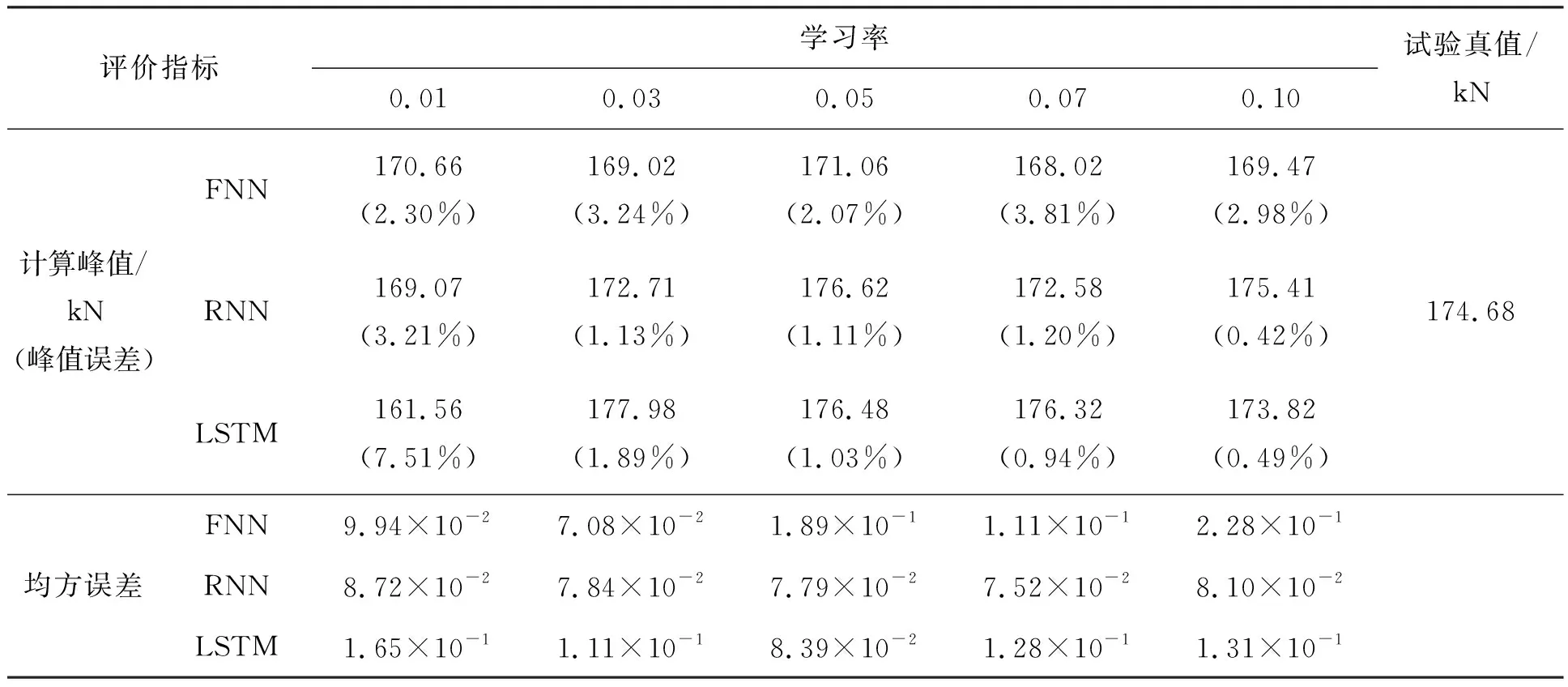
表1 不同学习率的模型精度
学习率影响着网络训练过程中梯度下降的速度,学习率过低容易使网络在训练过程中陷入局部极小,太大又会出现训练发散的情况。从图 8中可以看出,FNN的均方误差波动增长,且峰值误差明显大于RNN与LSTM,开伞试验中峰值误差对开伞成功率的影响更为重要,从这两个方面看,FNN的性能不如循环网络;在两种循环网络的比较中,RNN的均方误差对学习率的变化并不敏感,LSTM的均方误差先减小后增大,整体变化范围较小且η=0.05时有最小值,二者的峰值误差随着学习率的增大有逐渐下降的趋势,且学习率较小时LSTM的峰值误差变化率较大。综合图8与表1数据,在使用循环网络模型进行训练时,为保证训练要求,学习率选取0.05,训练结果稳定且精度较高。
实验还比较了学习率为0.05时,LSTM网络在不同输入维度与隐层维度下的峰值误差,如图9所示。其中,输入层维度变化时,固定隐层维度h=8;隐层维度变化时,固定输入层维度n=10。从图中可以明显看出,当输入层维度n=10、隐藏层维度h=8时,峰值误差取得最小值,模型训练结果具有最优解。
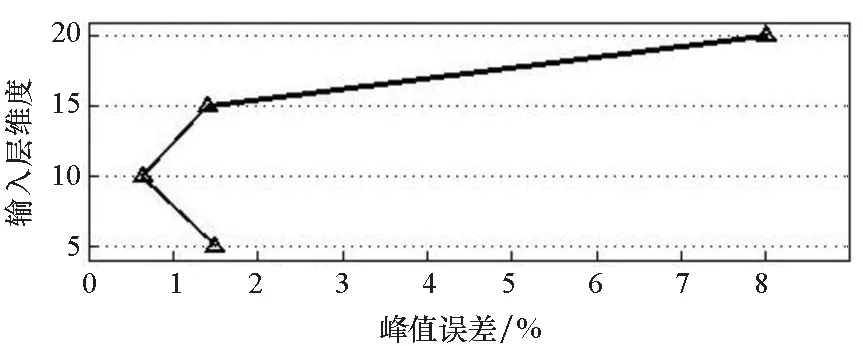
(a) 不同输入层的峰值误差变化(a) Peak error variation of different input layers
上述实验的训练过程中发现,隐层维度取某些值时,网络训练极易成功,而取某些值时却连续多次训练未收敛,由此现象本文探究了隐层维度对网络训练成功率的影响。由于计算资源有限,本实验统计了5个隐层维度下各20次训练后的网络收敛次数,图 10为统计数据融合峰值误差的结果,以颜色表示训练的难易程度。其中隐层维度h=8时训练成功次数明显高于其他情况,随着隐层维度的变化,训练成功率曲线整体类似于正态分布曲线。因此,综合图 8、图 9及图 10三组实验结果可知,本文采用的开伞载荷补偿模型在使用LSTM时的参考超参数为:学习率η=0.05、输入层维度n=10、隐层维度h=8。采用该参数组合时最容易获得优质补偿结果,且结果可复现能力强。
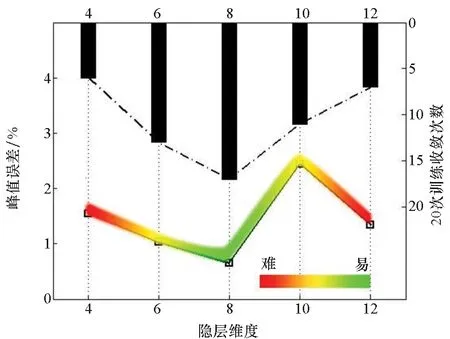
图10 不同隐层维度下的网络收敛次数Fig.10 Number of convergence with different hidden layer dimension
5 结论
针对降落伞开伞载荷的预测,建立了一种利用循环网络的载荷补偿方法,该方法在经验公式的计算结果上进行二次计算,使最终结果更加贴近试验真值。本文比较了三种网络模型的补偿结果,探讨了学习率对实验精度的影响,并重点分析了LSTM模型中超参数的选择,得到以下结论:
1)开伞载荷补偿模型可以正确反映拉力变化趋势,相较经验公式计算的开伞力,经过补偿的曲线更加贴合试验真值。
2)本模型中循环网络性能明显优于前馈网络,随着学习率增大,两种循环网络的峰值误差逐渐减小,为保证训练要求,用于训练的推荐学习率为0.05。
3)当学习率为0.05时,LSTM在输入层维度n=10、隐层维度h=8的条件下最容易获得优质补偿结果,且结果可复现能力强。
另外,本文建立的开伞载荷补偿模型作为机器学习与经典力学两种方向的交叉学科研究,目前仍处于初步探索阶段,方法仍有很大的改进空间,如预测结果的数据规律未能表现出盘-缝-带伞的拉力波动变化以及参与训练的样本特征较为单一等;除此之外,结合实践经验,还有高低空开伞试验数据归一化方法引起的数据分布不均与不同组试验传感器差异引起的样本特征种类不一致等问题有待进一步的解决,上述方向可为其他学者的继续研究提供一定的参考。

